Abbildungen innerhalb einer Ebene¶
Durch eine geometrische Abbildung entsteht aus einer Original-Figur eine neue Figur innerhalb der gleichen Ebene (beziehungsweise innerhalb des gleichen Raumes im dreidimensionalen Fall). Fasst man eine geometrische Form als Menge ihrer Punkte auf, so ist eine geometrische Abbildung formal mit einer Abbildung von Mengen identisch.
Ähnlichkeitsabbildungen¶
Bei einer Ähnlichkeitsabbildung bleibt die Form einer geometrischen Figur erhalten, ihre Größe ändert sich jedoch. Grundlegend ist hierbei die so genannte „zentrische Streckung“.
Um eine zentrische Streckung zu beschreiben, geht man von einem bestimmten Punkt
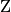 als Streckungszentrum aus. Zeichnet man von
als Streckungszentrum aus. Zeichnet man von 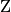 aus
durch jeden Punkt
aus
durch jeden Punkt  einer geometrischen Figur
einer geometrischen Figur 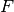 einen
Strahl und zeichnet auf diesem in der jeweils
einen
Strahl und zeichnet auf diesem in der jeweils 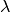 -fachen Entfernung einen
neuen Punkt
-fachen Entfernung einen
neuen Punkt 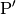 ein, so erhält man eine zweite Figur
ein, so erhält man eine zweite Figur 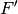 , die
gegenüber der Original-Figur verschoben und
, die
gegenüber der Original-Figur verschoben und 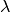 -mal so groß erscheint.[1]
-mal so groß erscheint.[1]
Der Faktor 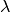 wird Skalierungsfaktor (umgangssprachlich auch
als „Maßstab“) genannt. Für
wird Skalierungsfaktor (umgangssprachlich auch
als „Maßstab“) genannt. Für 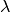 ergibt sich folgender
Zusammenhang:
ergibt sich folgender
Zusammenhang:
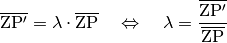
Ist 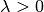 , so bleibt die Orientierungsrichtung der Figur, also der
Umlaufsinn ihrer Punkte, erhalten. Gilt
, so bleibt die Orientierungsrichtung der Figur, also der
Umlaufsinn ihrer Punkte, erhalten. Gilt 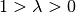 , so wird die Figur
verkleinert („gestaucht“), im Fall
, so wird die Figur
verkleinert („gestaucht“), im Fall 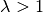 wird sie vergrößert
(„gestreckt“). Für
wird sie vergrößert
(„gestreckt“). Für 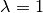 wird die Figur identisch auf sich selbst
abgebildet.
wird die Figur identisch auf sich selbst
abgebildet.
Ist 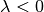 , so liegt die Bildfigur
, so liegt die Bildfigur 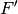 im Vergleich zur
Originalfigur
im Vergleich zur
Originalfigur 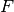 auf der gegenüber liegenden Seite des Zentrums
auf der gegenüber liegenden Seite des Zentrums
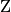 ; ihre Orientierungsrichtung bleibt dabei erhalten. Gilt
; ihre Orientierungsrichtung bleibt dabei erhalten. Gilt
 , so wird auch hierbei die Figur verkleinert beziehungsweise im
Fall
, so wird auch hierbei die Figur verkleinert beziehungsweise im
Fall 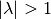 vergrößert.
vergrößert.
Bei jeder Ähnlichkeitsabbildung einer Figur 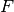 auf eine Figur
auf eine Figur 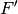 haben einerseits alle entsprechenden Strecken das gleiche Größenverhältnis
haben einerseits alle entsprechenden Strecken das gleiche Größenverhältnis
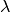 , andererseits bleiben die Größen aller Winkel der Figur
, andererseits bleiben die Größen aller Winkel der Figur 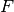 in
der Figur
in
der Figur 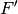 erhalten. Beide Kriterien können auch genutzt werden, um
„Ähnlichkeit“ als eine Relation zwischen zwei Figuren
aufzufassen: Zwei Figuren
erhalten. Beide Kriterien können auch genutzt werden, um
„Ähnlichkeit“ als eine Relation zwischen zwei Figuren
aufzufassen: Zwei Figuren 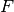 und
und 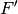 sind genau dann einander
ähnlich, wenn sie in ihren Winkeln übereinstimmen und die entsprechenden
Strecken im gleichen Maßstab zueinander stehen. In der mathematischen Kurzform
schreibt man hierfür
sind genau dann einander
ähnlich, wenn sie in ihren Winkeln übereinstimmen und die entsprechenden
Strecken im gleichen Maßstab zueinander stehen. In der mathematischen Kurzform
schreibt man hierfür 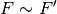 .
.
Kongruenzabbildungen¶
Als Kongruenzabbildung oder „Bewegung“ wird jede Abbildung bezeichnet, bei der die Original-Figur und ihr Abbild in Form und Größe übereinstimmen, sich also nur die Lage der Figur im Raum verändert. Lässt sich eine geometrische Figur durch eine beliebige Anzahl von Bewegungen deckungsgleich in eine andere Figur überführen, so nennt man die beiden Figuren kongruent; kongruente Figuren haben stets gleich lange Strecken und gleich große Winkel.[2]
Die vier möglichen Kongruenzabbildungen werden im Folgenden kurz aufgelistet:
Translation einer geometrischen Figur
Um eine Verschiebung („Translation“) zu beschreiben, geht man von einem Vektor
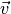 aus, für deren Länge
aus, für deren Länge 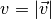 gelten soll. Trägt
man an jedem Punkt
gelten soll. Trägt
man an jedem Punkt  einer geometrischen Figur einen ebenso langen,
zu
einer geometrischen Figur einen ebenso langen,
zu 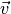 parallelen Vektor mit
parallelen Vektor mit  als Anfangspunkt an, so
ergibt sich zu jedem Original-Punkt ein zugehöriger Bildpunkt
als Anfangspunkt an, so
ergibt sich zu jedem Original-Punkt ein zugehöriger Bildpunkt 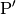 .
.
Die sich ergebende Bildfigur 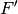 wird durch den Verschiebungsvektor
wird durch den Verschiebungsvektor
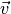 gegenüber der Original-Figur
gegenüber der Original-Figur 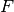 lediglich um die Länge
lediglich um die Länge
 in Richtung von
in Richtung von 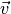 verschoben; die Größe, Form und
Orientierung der Figur bleiben hingegen erhalten.
verschoben; die Größe, Form und
Orientierung der Figur bleiben hingegen erhalten.
Spiegelung einer geometrischen Figur an einer Geraden
Um eine Spiegelung an einer Geraden zu beschreiben, geht man von einer festen
Geraden  als Spiegelachse aus. Durch jeden Punkt
als Spiegelachse aus. Durch jeden Punkt  einer Figur
konstruiert man eine Gerade senkrecht zu
einer Figur
konstruiert man eine Gerade senkrecht zu  und bestimmt auf dieser den
Bildpunkt
und bestimmt auf dieser den
Bildpunkt 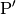 so, dass
so, dass  und
und 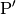 von
der Spiegelachse
von
der Spiegelachse  den gleichen Abstand haben und auf verschiedenen
Seiten von
den gleichen Abstand haben und auf verschiedenen
Seiten von  liegen.
liegen.
Der Punkt 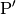 wird üblicherweise Spiegelbild von
wird üblicherweise Spiegelbild von  bezüglich
bezüglich  bezeichnet. Bei einer Achsenspiegelung bleibt die Form und
Größe der Figur erhalten, es ändert sich jedoch der Umlaufsinn ihrer Punkte.
bezeichnet. Bei einer Achsenspiegelung bleibt die Form und
Größe der Figur erhalten, es ändert sich jedoch der Umlaufsinn ihrer Punkte.
Spiegelung einer geometrischen Figur an einem Punkt
Um eine Spiegelung an einem Punkt zu beschreiben, geht man von einem festen
Punkt 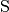 als Symmetriezentrum aus. Durch jeden Punkt
als Symmetriezentrum aus. Durch jeden Punkt
 einer Figur legt man dann eine Gerade durch
einer Figur legt man dann eine Gerade durch
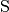 und bestimmt auf dieser den Bildpunkt
und bestimmt auf dieser den Bildpunkt 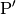 so,
dass
so,
dass  und
und 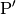 von
von 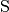 den
gleichen Abstand haben und auf verschiedenen Seiten von
den
gleichen Abstand haben und auf verschiedenen Seiten von 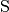 liegen.
liegen.
Man kann eine Punktspiegelung ebenso als zentrische Streckung mit einem Maßstab
von 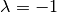 oder als Drehung der Ebene um den Punkt
oder als Drehung der Ebene um den Punkt  mit
einem Drehwinkel von
mit
einem Drehwinkel von ![\alpha=\unit[180]{\degree}](../../_images/math/f96f6369156e92a61de51ffc1a51bcaf8dbd3f80.png) deuten. Bei einer
Punktspiegelung bleibt somit neben der Form und Größe einer Figur auch ihr
Umlaufsinn, also die Reihenfolge ihrer Punkte erhalten.
deuten. Bei einer
Punktspiegelung bleibt somit neben der Form und Größe einer Figur auch ihr
Umlaufsinn, also die Reihenfolge ihrer Punkte erhalten.
Rotation einer geometrischen Figur
Um eine Drehung („Rotation“) zu beschreiben, geht man von einem bestimmten Punkt
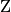 als Drehzentrum und einem festen Winkel
als Drehzentrum und einem festen Winkel 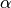 aus. Durch
jeden Punkt
aus. Durch
jeden Punkt  einer Figur zeichnet man einen Kreis um den
Mittelpunkt
einer Figur zeichnet man einen Kreis um den
Mittelpunkt 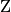 und bestimmt auf diesem Kreis den zu
und bestimmt auf diesem Kreis den zu  gehörenden Bildpunkt
gehörenden Bildpunkt 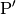 so, dass der Winkel
so, dass der Winkel 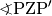 gleich
gleich 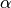 ist.
ist.
Erfolgt die Drehung entgegengesetzt zum Uhrzeigersinn, so spricht man von einem positiven Drehsinn; bei einer Drehung im Uhrzeigersinn spricht man von einem negativen Drehsinn. Die Form und Größe der Figur sowie die Reihenfolge ihrer Punkte bleibt bei einer Drehung erhalten.
Anmerkung:
| [1] | In der analytischen Geometrie werden Skalierungen von geometrischen Objekten rechnerisch mittels Skalierungsmatrizen beschrieben. |
| [2] | Jede Kongruenzabbildung kann auch als eine Ähnlichkeitsabbildung
mit einem Maßstab von 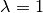 aufgefasst werden. Umgekehrt lässt
sich jede Ähnlichkeitsabbildung aus einer zentrischen Streckung und/oder
einer oder mehreren Kongruenzabbildungen zusammensetzen. aufgefasst werden. Umgekehrt lässt
sich jede Ähnlichkeitsabbildung aus einer zentrischen Streckung und/oder
einer oder mehreren Kongruenzabbildungen zusammensetzen. |



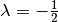 .
.


