Grundkonstruktionen¶
Auch wenn heutzutage ausgereifte Geometrie- und Zeichenprogramme wie Geogebra oder Inkscape frei verfügbar und weit verbreitet sind, so sind im praktischen Einsatz oftmals auch einfache Zeichentechniken nützlich, die sich mit Zirkel und Lineal beziehungsweise Geodreieck umsetzen lassen. Solche Grundkonstruktionen sind:
Eine Strecke halbieren:
Zunächst zeichnet man von beiden Endpunkten
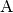 und
und
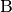 der Strecke aus je einen Kreis mit Radius
der Strecke aus je einen Kreis mit Radius 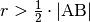 . Beide Kreise schneiden sich in zwei
Punkten
. Beide Kreise schneiden sich in zwei
Punkten 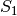 und
und 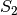 . Die Verbindungslinie dieser beiden
Schnittpunkte halbiert die Strecke
. Die Verbindungslinie dieser beiden
Schnittpunkte halbiert die Strecke 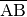 .
.Eine Senkrechte zu einer Strecke
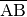 errichten, die
durch einen bestimmten Punkt
errichten, die
durch einen bestimmten Punkt  auf der Strecke verläuft:
auf der Strecke verläuft:Zunächst zeichnet man um den Punkt
 einen Kreis mit
beliebigem Radius
einen Kreis mit
beliebigem Radius 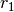 . Anschließend zeichnet man um die beiden
Schnittpunkte
. Anschließend zeichnet man um die beiden
Schnittpunkte 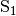 und
und 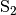 zwei weitere
Kreise, jeweils mit Radius
zwei weitere
Kreise, jeweils mit Radius 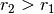 . Die Strecke vom Punkt
. Die Strecke vom Punkt
 zu einem der beiden sich ergebenden Schnittpunkte
zu einem der beiden sich ergebenden Schnittpunkte
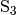 und
und 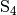 entspricht der gesuchten
Senkrechten.
entspricht der gesuchten
Senkrechten.Eine Senkrechte zu einer Strecke
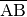 errichten, die
durch einen externen Punkt
errichten, die
durch einen externen Punkt  verläuft:
verläuft:Zunächst zeichnet man um den Punkt
 einen Kreis mit Radius
einen Kreis mit Radius
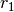 , so dass dieser die Strecke in den Punkten
, so dass dieser die Strecke in den Punkten 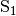 und
und 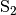 schneidet. Anschliessend zeichnet man um die beiden
Schnittpunkte
schneidet. Anschliessend zeichnet man um die beiden
Schnittpunkte 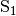 und
und 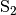 zwei weitere
Kreise, jeweils mit Radius
zwei weitere
Kreise, jeweils mit Radius 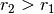 . Die Strecke vom Punkt
. Die Strecke vom Punkt
 zu einem der beiden sich ergebenden Schnittpunkte,
vorzugsweise zum gegenüber liegenden Punkt
zu einem der beiden sich ergebenden Schnittpunkte,
vorzugsweise zum gegenüber liegenden Punkt 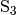 , entspricht
der gesuchten Senkrechten.
, entspricht
der gesuchten Senkrechten.Eine Parallele zu einer Strecke
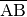 errichten, die
durch einen externen Punkt
errichten, die
durch einen externen Punkt  geht:
geht:Zunächst zeichnet man eine vom Punkt
 ausgehende Halbgerade,
welche die Strecke in einem (beliebigen) Punkt
ausgehende Halbgerade,
welche die Strecke in einem (beliebigen) Punkt 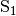 schneidet.
Anschließend zeichnet man um
schneidet.
Anschließend zeichnet man um 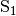 einen Kreis mit Radius
einen Kreis mit Radius
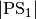 . Zeichne anschließend vom Schnittpunkt
. Zeichne anschließend vom Schnittpunkt
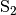 dieses Kreises mit der Halbgeraden eine weitere
Halbgerade durch einen anderen (beliebigen) Punkt
dieses Kreises mit der Halbgeraden eine weitere
Halbgerade durch einen anderen (beliebigen) Punkt 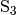 auf der
Strecke. Ein Kreis um
auf der
Strecke. Ein Kreis um 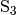 mit dem Radius
mit dem Radius
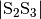 liefert den Schnittpunkt
liefert den Schnittpunkt 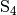 . Die
Gerade entlang
. Die
Gerade entlang 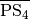 entspricht schließlich der
gesuchten Parallele.
entspricht schließlich der
gesuchten Parallele.Hat man nicht nur einen Zirkel und ein Lineal, sondern zusätzlich ein Konstruktions-Dreieck, so kann man auch dieses nutzen, um eine parallele Gerade zu konstruieren: Man legt zunächst das Dreieck mit einer Seite entlang der Geraden an; anschließend legt man das Lineal entlang einer der beiden anderen Dreieckseiten an. Verschiebt man nun das Dreieck längs des Lineals, so kann man entlang der Dreieckseite, die entlang der ursprünglichen Gerade verlief, unmittelbar eine parallel verlaufende Strecke zeichnen.
Einen Winkel halbieren:
Zunächst zeichnet man um den Scheitelpunkt des Winkels einen Kreis mit beliebigem Radius, der die Winkelschenkel in den Punkten
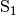 und
und 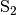 schneidet. Um diese zeichnet man anschließend zwei
weitere Kreise mit gleichem Radius. Der Schnittpunkt
schneidet. Um diese zeichnet man anschließend zwei
weitere Kreise mit gleichem Radius. Der Schnittpunkt 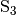 dieser beiden Kreise liefert, verbunden mit dem Scheitelpunkt des Winkels, die
gesuchte Winkelhalbierende.
dieser beiden Kreise liefert, verbunden mit dem Scheitelpunkt des Winkels, die
gesuchte Winkelhalbierende.






