Symmetrie¶
Als Symmetrie wird die Eigenschaft mancher geometrischer Formen bezeichnet, nach einer bestimmten Transformation wiederum unverändert zu erscheinen.
Achsensymmetrie¶
Eine beliebige, quer durch eine geometrische Figur verlaufende Gerade oder Strecke wird Transversale genannt. Lässt sich die Figur durch eine dieser Transversalen in zwei gleiche große Teilfiguren aufteilen, die durch Umklappen entlang der Transversalen völlig deckungsgleich zueinander sind, so heißt die Figur achsensymmetrisch. Die beiden Teilstücke der Figur werden dabei als einander entsprechend bezeichnet und die Transversale Symmetrieachse genannt.
Eine Figur kann auch mehrere Symmetrieachsen besitzen. Beispielsweise besitzt ein Rechteck zwei Symmetrieachsen, ein Kreis sogar beliebig viele.
Lassen sich zwei gleich große Figuren durch Umklappen um eine zwischen beiden
Figuren liegende Gerade  zur Deckung bringen, so bezeichnet man beide
Figuren als achsensymmetrisch zueinander liegend. Achsensymmetrische Figuren
haben stets folgende Eigenschaften:
zur Deckung bringen, so bezeichnet man beide
Figuren als achsensymmetrisch zueinander liegend. Achsensymmetrische Figuren
haben stets folgende Eigenschaften:
- Einander entsprechende Punkte liegen gleich weit von der Symmetrieachse
 entfernt.
entfernt. - Verbindungslinien zwischen einander entsprechenden Punkten stehen senkrecht auf der Symmetrieachse.
- Einander entsprechende Geraden (sowie Strecken und ihre Verlängerungen) schneiden die Symmetrieachse im gleichen Punkt und im gleichen Winkel.
- Der Umlaufsinn beider Figuren ist umgekehrt, entsprechende Ecken folgen in der einen Figur also im Uhrzeigersinn aufeinander, in der anderen entgegen dem Uhrzeigersinn.
Achsensymmetrische Figuren können ebenso als Paare von achsensymmetrisch liegenden Figuren aufgefasst werden, deren Flächen sich zum Teil überschneiden.
Punktsymmetrie¶
Ist eine Figur bei einer 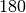 -Drehung um einen im Inneren gelegenen
Punkt völlig deckungsgleich mit sich selbst, so heißt die Figur (einfach)
punktsymmetrisch. Der Drehpunkt wird dabei als Symmetriezentrum, der Drehwinkel
als Symmetriewinkel bezeichnet.
-Drehung um einen im Inneren gelegenen
Punkt völlig deckungsgleich mit sich selbst, so heißt die Figur (einfach)
punktsymmetrisch. Der Drehpunkt wird dabei als Symmetriezentrum, der Drehwinkel
als Symmetriewinkel bezeichnet.
Ist eine Figur bereits nach einer Drehung um einen Winkel 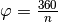 mit sich selbst deckungsgleich, wobei
mit sich selbst deckungsgleich, wobei 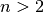 eine
beliebige natürliche Zahl ist, so heißt die Figur mehrfach punktsymmetrisch.
Sie ist bei weiteren Drehungen um den Winkel
eine
beliebige natürliche Zahl ist, so heißt die Figur mehrfach punktsymmetrisch.
Sie ist bei weiteren Drehungen um den Winkel 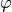 stets erneut
deckungsgleich.
stets erneut
deckungsgleich.
Lassen sich zwei gleich große Figuren durch eine 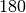 -Drehung um einen
zwischen beiden Figuren liegenden Punkt
-Drehung um einen
zwischen beiden Figuren liegenden Punkt  zur Deckung bringen, so
bezeichnet man beide Figuren als punktsymmetrisch zueinander liegend.
Punktsymmetrische Figuren haben stets folgende Eigenschaften:
zur Deckung bringen, so
bezeichnet man beide Figuren als punktsymmetrisch zueinander liegend.
Punktsymmetrische Figuren haben stets folgende Eigenschaften:
- Einander entsprechende Punkte liegen gleich weit vom Symmetriezentrum
 entfernt.
entfernt. - Verbindungslinien zwischen einander entsprechenden Punkten verlaufen durch das Symmetriezentrum.
- Einander entsprechende Geraden (sowie Strecken und ihre Verlängerungen) verlaufen zueinander parallel.
- Der Umlaufsinn beider Figuren ist gleich, entsprechende Ecken folgen in beiden Figuren also entweder im Uhrzeigersinn oder entgegen dem Uhrzeigersinn aufeinander.
Punktsymmetrische Figuren können ebenso als Paare von punktsymmetrisch liegenden Figuren aufgefasst werden, deren Flächen sich zum Teil überschneiden.




