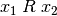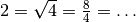Abbildungen, Funktionen, Relationen und Operationen¶
Abbildungen¶
Unter einer Abbildung 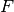 aus einer Menge
aus einer Menge 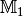 in eine
Menge
in eine
Menge 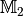 versteht man eine Teilmenge der Produktmenge
versteht man eine Teilmenge der Produktmenge 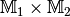 .
.
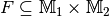
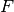 ist somit eine Menge von geordneten Paaren
ist somit eine Menge von geordneten Paaren 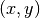 mit
mit 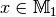 und
und 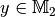 . Man sagt, dass durch die
Abbildung
. Man sagt, dass durch die
Abbildung 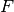 das Element
das Element  dem Element
dem Element  zugeordnet wird.[1] Die Mengen
zugeordnet wird.[1] Die Mengen 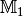 und
und 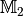 können auch gleich
sein.
können auch gleich
sein.
Beispiel:
- Durch eine Abbildung
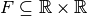 kann
beispielsweise jeder reellen Zahl
kann
beispielsweise jeder reellen Zahl  ihre Quadratzahl
ihre Quadratzahl 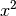 zugeordnet werden. Es ist dann
zugeordnet werden. Es ist dann 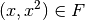 für alle
für alle 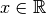 .
.
Die Menge aller 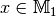 , für die ein
, für die ein 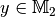 existiert, nennt man Definitionsbereich der Abbildung;
entsprechend nennt man die Menge aller
existiert, nennt man Definitionsbereich der Abbildung;
entsprechend nennt man die Menge aller 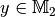 , für die ein
zugehöriges
, für die ein
zugehöriges 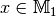 existiert, Wertebereich der Abbildung.
existiert, Wertebereich der Abbildung.
Inverse Abbildung
Unter einer inversen Abbildung 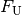 (auch „Umkehrabbildung“
genannt) versteht man die Menge aller geordneten Paare
(auch „Umkehrabbildung“
genannt) versteht man die Menge aller geordneten Paare 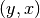 , für die
, für die
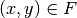 gilt.
gilt.
Der Definitionsbereich der inversen Abbildung ist der Wertebereich der ursprünglichen Abbildung und umgekehrt; die inverse Abbildung der inversen Abbildung ist mit der ursprünglichen Abbildung identisch.
Verkettung von Abbildungen
Es sei 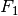 eine Abbildung von
eine Abbildung von 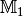 in
in
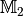 und
und 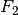 eine Abbildung aus
eine Abbildung aus 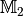 in
in
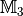 . Eine Abbildung
. Eine Abbildung 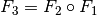 (gelesen:
„
(gelesen:
„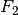 verkettet mit
verkettet mit 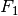 „) wird dann als Verkettung
(Hintereinanderausführung) bezeichnet, wenn für alle geordneten Paare
„) wird dann als Verkettung
(Hintereinanderausführung) bezeichnet, wenn für alle geordneten Paare
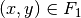 und
und 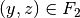 gilt:
gilt: 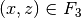 .
.
Allgemein gilt für Verkettungen von Abbildungen zwar das Assoziativgesetz nicht, die Reihenfolge der Abbildungen ist also nicht vertauschbar; jedoch gilt das Assoziativ-Gesetz in folgender Form:
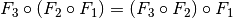
Für eindeutige Abbildungen (Funktionen) ist folgende Darstellung üblich:
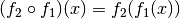
Man nennt dabei die Funktion 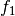 die innere Funktion und
die innere Funktion und 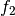 die
äußere Funktion der Verkettung. Somit ist die Reihenfolge der Verkettung
(„
die
äußere Funktion der Verkettung. Somit ist die Reihenfolge der Verkettung
(„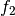 nach
nach 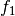 „) gut erkennbar.
„) gut erkennbar.
Beispiel:
- Es sei
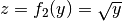 sowie
sowie 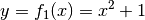 . Somit gilt
. Somit gilt 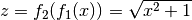 .
.
Funktionen¶
Eine Abbildung  aus
aus 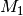 in
in 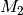 heißt eindeutig, wenn
jedem
heißt eindeutig, wenn
jedem 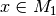 höchstens ein
höchstens ein 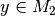 zugeordnet wird.
Eine derartige Abbildung
zugeordnet wird.
Eine derartige Abbildung  wird Funktion genannt; man bezeichnet sie im
Allgemeinen mit einem kleinen lateinischen Buchstaben.
wird Funktion genannt; man bezeichnet sie im
Allgemeinen mit einem kleinen lateinischen Buchstaben.
Jedem  im Definitionsbereich von
im Definitionsbereich von  wird somit genau ein Wert
wird somit genau ein Wert
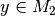 zugeordnet. Der Mathematiker Leonhard Euler hat hierfür die Schreibweise
zugeordnet. Der Mathematiker Leonhard Euler hat hierfür die Schreibweise
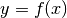 eingeführt. Dabei wird die Variable
eingeführt. Dabei wird die Variable  als Argument der
Funktion
als Argument der
Funktion  bezeichnet,
bezeichnet, 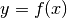 wird Funktionswert genannt.
wird Funktionswert genannt.
Zwei Funktionen sind gleich, wenn sie für jedes 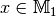 den
gleichen Funktionswert
den
gleichen Funktionswert 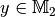 liefern, also
liefern, also 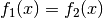 für alle
für alle 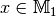 gilt.
gilt.
Ist auch die inverse Abbildung 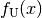 einer Funktion
einer Funktion 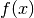 eindeutig, so nennt man die Funktion
eindeutig, so nennt man die Funktion 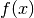 (eindeutig) umkehrbar; die
Funktion
(eindeutig) umkehrbar; die
Funktion 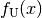 wird entsprechend als Umkehrfunktion bezeichnet. Sie
entspricht der Menge an geordneten Paaren
wird entsprechend als Umkehrfunktion bezeichnet. Sie
entspricht der Menge an geordneten Paaren 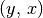 , für die
, für die
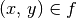 gilt. Auch in diesem Fall ist der Definitionsbereich
der Umkehrfunktion der Wertebereich der ursprünglichen Funktion und umgekehrt.
gilt. Auch in diesem Fall ist der Definitionsbereich
der Umkehrfunktion der Wertebereich der ursprünglichen Funktion und umgekehrt.
Funktionen sind insbesondere in der Analysis von zentraler Bedeutung.
Relationen¶
Eine Relation 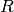 ist eine Abbildung aus einer Menge
ist eine Abbildung aus einer Menge 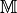 in
die gleiche Menge
in
die gleiche Menge 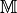 . Von besonderer Bedeutung sind zweistellige
Relationen, also Teilmengen von
. Von besonderer Bedeutung sind zweistellige
Relationen, also Teilmengen von 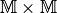 .
.
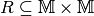
Wenn für ein geordnetes Paar 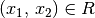 gilt, so sagt man,
dass
gilt, so sagt man,
dass  und
und 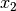 in der Relation
in der Relation 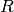 zueinander stehen. In
mathematischer Form schreibt man:
zueinander stehen. In
mathematischer Form schreibt man:
Beispiel:
Es sei
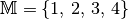 und
und 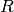 die „Kleiner als“-Relation
die „Kleiner als“-Relation 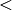 . Dann gilt:
. Dann gilt: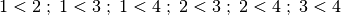
Alle durch die „Kleiner als“-Relation verknüpften Zahlen lassen sich als geordnete Paare darstellen:
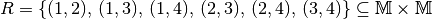
Nach dem gleichen Prinzip lassen sich auch drei- und mehrstellige Relationen
bilden, beispielsweise „ liegt zwischen
liegt zwischen  und
und  „.[2]
Darüber hinaus gelten auch für Relationen die allgemeinen Eigenschaften von
Abbildungen; beispielsweise kann eine Relation
„.[2]
Darüber hinaus gelten auch für Relationen die allgemeinen Eigenschaften von
Abbildungen; beispielsweise kann eine Relation 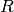 mit
mit 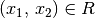 durch Bildung der entsprechenden Paare
durch Bildung der entsprechenden Paare 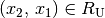 invertiert werden. Ebenfalls lassen sich zwei Relationen
invertiert werden. Ebenfalls lassen sich zwei Relationen
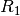 und
und 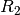 zu einer einzigen Relation
zu einer einzigen Relation 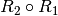 verketten.
verketten.
Reflexivität, Symmetrie und Transitivität
Verschiedene Relationen lassen sich hinsichtlich drei charakteristischer Eigenschaften unterscheiden:
- Reflexivität:
Eine Relation
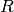 in einer Menge
in einer Menge 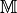 heißt reflexiv,
wenn jedes
heißt reflexiv,
wenn jedes 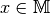 in Relation zu sich selbst steht, also
für alle
in Relation zu sich selbst steht, also
für alle  gilt:
gilt: 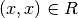
Beispiele:
- Die „Kleiner/Gleich“-Relation
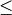 ist für die Menge
ist für die Menge
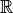 der reellen Zahlen reflexiv, denn es gilt
der reellen Zahlen reflexiv, denn es gilt 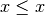 für alle
für alle 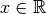 :
: - Die „Kleiner“-Relation
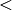 ist, ebenfalls bezogen auf die Menge
ist, ebenfalls bezogen auf die Menge
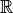 der reellen Zahlen, nicht reflexiv.
der reellen Zahlen, nicht reflexiv.
- Die „Kleiner/Gleich“-Relation
- Symmetrie:
Eine Relation
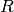 in einer Menge
in einer Menge 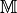 heißt symmetrisch,
wenn für alle
heißt symmetrisch,
wenn für alle 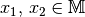 aus dem Zutreffen von
aus dem Zutreffen von
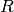 auf
auf 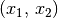 auch das Zutreffen von
auch das Zutreffen von 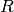 auf
auf
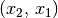 folgt.[3]
folgt.[3]Beispiel:
- Für alle Geraden
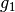 und
und 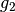 ist die
Relation „
ist die
Relation „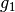 steht senkrecht auf
steht senkrecht auf 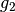 “
symmetrisch.
“
symmetrisch.
- Für alle Geraden
- Transitivität:
Eine Relation
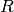 in einer Menge
in einer Menge 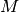 heißt transitiv, wenn für
alle
heißt transitiv, wenn für
alle 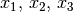 aus dem Zutreffen von
aus dem Zutreffen von 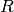 auf
auf
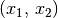 und dem Zutreffen von
und dem Zutreffen von 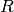 auf
auf 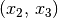 auch das Zutreffen von
auch das Zutreffen von 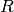 auf
auf 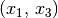 folgt.
folgt.Beispiel:
- Die Kleiner-Relation
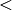 für reelle Zahlen ist transitiv, denn gilt
für je drei beliebige reelle Zahlen
für reelle Zahlen ist transitiv, denn gilt
für je drei beliebige reelle Zahlen 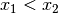 sowie
sowie 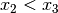 , so gilt ebenfalls
, so gilt ebenfalls 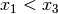 .
.
- Die Kleiner-Relation
Eine weitere wichtige Eigenschaft vieler Relationen ist die so genannte
„Linearität“. Eine Relation 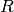 in einer Menge
in einer Menge 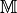 heißt
linear, wenn entweder
heißt
linear, wenn entweder 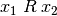 oder
oder 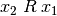 gilt. Ein Beispiel hierfür ist die „Kleiner-Gleich“-Relation
gilt. Ein Beispiel hierfür ist die „Kleiner-Gleich“-Relation 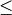 für reelle Zahlen
für reelle Zahlen 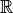 , denn es gilt für alle
, denn es gilt für alle 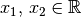 stets entweder
stets entweder 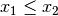 oder
oder 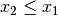 .
.
Ordnungs- und Äquivalenzrelationen
Zwei Relationstypen sind in der Mathematik von besonderer Bedeutung:
1.: Ordnungsrelationen:
Es gibt verschiedene Ordnungsrelationen; sie haben gemeinsam, dass sie transitiv sind, unterscheiden sich jedoch in ihren weiteren Eigenschaften.
Beispiel:
- Eine wichtige Ordnungsrelation ist die so genannte „reflexive Ordnung“,
beispielsweise die „Kleiner/Gleich“-Relation
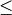 für die reellen
Zahlen. Sie ist reflexiv, antisymmetrisch, transitiv und linear.[4]
für die reellen
Zahlen. Sie ist reflexiv, antisymmetrisch, transitiv und linear.[4]
2.: Äquivalenzrelationen:
Äquivalenzrelationen sind Relationen, die sowohl reflexiv als auch symmetrisch und transitiv sind.
Beispiele:
- Die wohl wichtigste Äquivalenzrelation ist die Gleichheit-Relation
 („Identität“) zweier reeller Zahlen. Offensichtlich gilt für jede reelle Zahl
(„Identität“) zweier reeller Zahlen. Offensichtlich gilt für jede reelle Zahl
 :
:  (Reflexivität); gilt zudem für zwei beliebige reelle
Zahlen
(Reflexivität); gilt zudem für zwei beliebige reelle
Zahlen 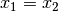 , so gilt auch
, so gilt auch 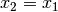 (Symmetrie); gilt
ferner für drei beliebige reelle Zahlen:
(Symmetrie); gilt
ferner für drei beliebige reelle Zahlen: 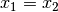 und
und  , so gilt ebenfalls
, so gilt ebenfalls 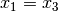 (Transitivität).
(Transitivität). - Die Kongruenz- und Ähnlichkeits-Relation zwischen geometrischen Körpern stellen ebenfalls Äquivalenzrelationen dar.
Durch eine Äquivalenz-Relation wird eine Menge 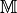 in
unterschiedliche Äquivalenz-Klassen zerlegt.[5] Jedes Element einer solchen
Klasse heißt Repräsentant der Klasse und steht mit allen anderen Elementen der
Klasse in der Relation
in
unterschiedliche Äquivalenz-Klassen zerlegt.[5] Jedes Element einer solchen
Klasse heißt Repräsentant der Klasse und steht mit allen anderen Elementen der
Klasse in der Relation 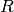 , es gilt also
, es gilt also 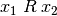 für alle
für alle 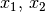 einer Äquivalenz-Klasse.[6]
einer Äquivalenz-Klasse.[6]
Alle Repräsentanten werden als nicht voneinander verschieden betrachtet, es wird
also davon abgesehen, dass sich die Elemente einer Äquivalenz-Klasse in gewissen
Eigenschaften unterscheiden. Somit sind Äquivalenzrelationen charakteristisch
für mathematische Abstraktionsprozesse: Eine Menge 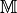 kann mit
Hilfe einer Äquivalenzrelation
kann mit
Hilfe einer Äquivalenzrelation 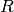 in ein System von Äquivalenz-Klassen
zerlegt werden. Diese Klassen treten somit an die Stelle ihrer Repräsentanten,
die wiederum anhand ihrer entsprechenden Klasse „identifiziert“ werden.
in ein System von Äquivalenz-Klassen
zerlegt werden. Diese Klassen treten somit an die Stelle ihrer Repräsentanten,
die wiederum anhand ihrer entsprechenden Klasse „identifiziert“ werden.
Operationen¶
Durch eine (zweistellige) Operation werden Elemente 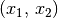 einer
Produkt-Menge
einer
Produkt-Menge 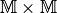 in eindeutiger Weise auf je
ein Element
in eindeutiger Weise auf je
ein Element  der Menge
der Menge 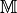 abgebildet. Mathematisch
schreibt man hierfür:
abgebildet. Mathematisch
schreibt man hierfür:
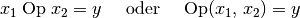
Das jeweilige Zeichen 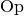 wird dabei als Operationszeichen (oder
kurz „Operator“) bezeichnet,
wird dabei als Operationszeichen (oder
kurz „Operator“) bezeichnet,  und
und 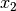 werden Operanden
genannt.[7]
werden Operanden
genannt.[7]
Beispiel:
- Durch die Operation der Addition (Operationszeichen:
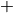 ) werden
beispielsweise zwei natürliche Zahlen
) werden
beispielsweise zwei natürliche Zahlen 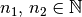 auf
eine natürliche Zahl
auf
eine natürliche Zahl 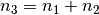 abgebildet.
abgebildet.
Nach dem gleichen Prinzip lassen sich auch ein- oder mehrstellige Operationen
als eindeutige Abbildungen von Elementen 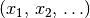 aus
aus
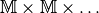 auf Elemente
auf Elemente 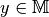 bilden.
bilden.
Beispiele:
- Durch die einstellige Operation „Bildung von
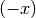 “ wird jede (reelle)
Zahl
“ wird jede (reelle)
Zahl  auf eine gleich große, negative Zahl abgebildet.
auf eine gleich große, negative Zahl abgebildet. - Durch die einstellige Operation „Bildung von
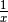 “ wird jede
(reelle) Zahl
“ wird jede
(reelle) Zahl 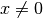 auf den Kehrwert der Zahl abgebildet.
auf den Kehrwert der Zahl abgebildet.
Eine Operation nennt man unbeschränkt ausführbar, wenn sie für alle Elemente
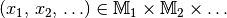 definiert ist; andernfalls nennt man sie beschränkt ausführbar. Im
Bereich der natürlichen Zahlen beispielsweise ist die Addition eine unbeschränkt
ausführbare, die Subtraktion hingegen eine nur beschränkt ausführbare Operation.
definiert ist; andernfalls nennt man sie beschränkt ausführbar. Im
Bereich der natürlichen Zahlen beispielsweise ist die Addition eine unbeschränkt
ausführbare, die Subtraktion hingegen eine nur beschränkt ausführbare Operation.
Eigenschaften von Operationen
Operationen können – je nach Operation und zugrunde liegender Menge – verschiedene Eigenschaften besitzen. Im folgenden werden mögliche Eigenschaften von zweistelligen Operationen aufgelistet, die entsprechend auch auf mehrstellige Operationen zutreffen können:
- Kommutativität:
Eine Operation
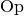 in einer Menge
in einer Menge 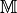 heißt
kommutativ genau dann, wenn für alle
heißt
kommutativ genau dann, wenn für alle 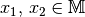 gilt:
gilt: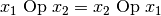
Ein Beispiel für eine kommutative Operation ist die Addition in der Menge der natürlichen Zahlen.
- Assoziativität:
Eine Operation
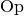 in einer Menge
in einer Menge 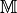 heißt
assoziativ genau dann, wenn für alle
heißt
assoziativ genau dann, wenn für alle 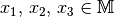 gilt:
gilt: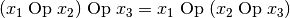
Ein Beispiel für eine assoziative Operation ist die Multiplikation in der Menge der reellen Zahlen.
- Distributivität:
Eine Operation
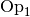 heißt in einer Menge
heißt in einer Menge 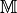 (linksseitig) distributiv bezüglich
(linksseitig) distributiv bezüglich 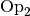 genau dann, wenn
für alle
genau dann, wenn
für alle 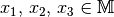 gilt:
gilt: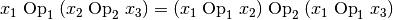
Ein Beispiel für eine distributive Operation mit den zwei Operatoren
 und
und 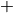 ist folgende Verknüpfung dreier reeller Zahlen
ist folgende Verknüpfung dreier reeller Zahlen
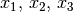 :
: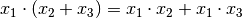
Anmerkungen:
| [1] | In diesem Zusammenhang wird  auch als „Urbild“ von auch als „Urbild“ von  beziehungsweise
beziehungsweise  als „Bild“ von als „Bild“ von  . . |
| [2] | Eine  -stellige Relation entsprechend eine Teilmenge -stellige Relation entsprechend eine Teilmenge
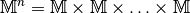 . . |
| [3] | Folgt im umgekehrten Fall aus dem Zutreffen von 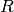 auf auf
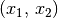 das Nicht-Zutreffen von das Nicht-Zutreffen von 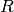 auf auf 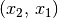 , so nennt man die Relation antisymmetrisch. , so nennt man die Relation antisymmetrisch. |
| [4] | Gilt die Linearität nicht, so spricht man von einer reflexiven
Halbordnung. Ein Beispiel hierfür ist die Teilbarkeitsrelation „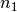 teilt
teilt 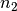 “ für zwei natürliche Zahlen. “ für zwei natürliche Zahlen. |
| [5] | Unter einer Zerlegung einer nichtleeren Menge Ebenfalls existiert zu jeder Zerlegung einer nichtleeren Menge
|
| [6] | Äquivalenz-Klassen reeller Zahlen, die durch Gleichheits-Relation
gebildet werden, bestehen jeweils aus genau einer Zahl, da jede Zahl nur mit
sich selbst identisch ist. Zahlen können allerdings meist auf
unterschiedliche Arten dargestellt werden; beispielsweise gilt Allgemein können Äquivalenz-Klassen beliebig viele Elemente beinhalten. Betrachtet man beispielsweise die Menge aller Fahrzeuge und die Relation „hat die gleiche Farbe wie“, so beinhalten die Äquivalenzklassen „rot“, „grün“, „blau“, usw. jeweils eine große Anzahl an Fahrzeugen. |
| [7] | Bei speziellen Operationen haben die Operanden eigene Bezeichnungen; im
Term 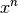 bezeichnet man beispielsweise bezeichnet man beispielsweise  als Basis und als Basis und
 als Exponent. als Exponent. |