Gleichungen

Lineare Gleichungen

Die folgenden Aufgaben beziehen sich auf den Abschnitt Lineare Gleichungen.

  • Für welchen Wert x gilt die folgende Gleichung?

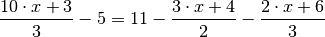
    \frac{10 \cdot x+3}{3} -5 = 11 - \frac{3 \cdot x + 4}{2} - \frac{2 \cdot x + 6}{3}

    Lösung

Quadratische Gleichungen

Die folgenden Aufgaben beziehen sich auf den Abschnitt Quadratische Gleichungen.

  • Welche Lösungsmengen haben folgende Gleichungen?

    \begin{array}{>{\arraybackslash$}p{8cm}<{$} >{\arraybackslash$}p{8cm}<{$}} \text{a) } x^2 - 6 \cdot x + 8 = 0 & \text{b) } 3 \cdot x^2 + 4 \cdot x - 15 = 0\\[12pt] \end{array}

    Lösung

  • Wie lässt sich folgende Gleichung mit Hilfe des Satzes von Vieta lösen?

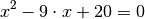
    x^2 - 9 \cdot x + 20 = 0

    Wie lautet die Produktform dieser Gleichung?

    Lösung

Algebraische Gleichungen

Die folgenden Aufgaben beziehen sich auf den Abschnitt Algebraische Gleichungen höheren Grades.

  • Von der folgenden Gleichung dritten Grades sei die Lösung 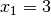x_1=3 bekannt. Wie lauten die anderen beiden Lösungen der Gleichung?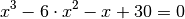

    x^3 - 6 \cdot x^2 - x + 30 = 0

    Lösung

  • Wie lauten die Lösungsmengen folgender Gleichungen?

    \begin{array}{>{\arraybackslash$}p{8cm}<{$} >{\arraybackslash$}p{8cm}<{$}} \text{a) } 2 \cdot x^3 - 5 \cdot x^2 - 12 \cdot x = 0 & \text{b) } x^4 - 13 \cdot x^2 + 36 = 0 \\[12pt] \end{array}

    Lösung

Bruch-, Produkt- und Wurzelgleichungen

Die folgenden Aufgaben beziehen sich auf den Abschnitt Bruch-, Produkt- und Wurzelgleichungen.

Bruch- und Produktgleichungen

  • Welche Lösungsmenge hat folgende Gleichung?

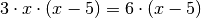
    3 \cdot x \cdot (x - 5) &= 6 \cdot (x - 5) \\

    Lösung

  • Welche Lösungsmenge hat folgende Gleichung?

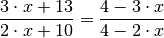
    \frac{3 \cdot x + 13}{2 \cdot x + 10} = \frac{4 - 3 \cdot x}{4 - 2\cdot x}

    Lösung

Wurzelgleichungen

  • Weshalb hat die folgende Gleichung keine Lösung?

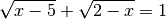
    \sqrt{x-5} + \sqrt{2-x} = 1

    Lösung

  • Welche Lösungsmengen haben folgende Gleichungen?

    \begin{array}{>{\arraybackslash$}p{8cm}<{$} >{\arraybackslash$}p{8cm}<{$}} \text{a) } \sqrt{x + 1} = x - 5 & \text{b) } \sqrt{3 \cdot x + 7} = 2 - 2 \cdot x \\[12pt] \end{array}

    Lösung

Exponential- und Logarithmusgleichungen

Die folgenden Aufgaben beziehen sich auf den Abschnitt Exponential- und Logarithmusgleichungen.

  • Welche Lösungsmengen haben folgende Exponential-Gleichungen?

    \begin{array}{>{\arraybackslash$}p{8cm}<{$} >{\arraybackslash$}p{8cm}<{$}} \text{a) } 3^x = 12 & \text{b) } 2^{2 \cdot x + 2} = 4^{3 \cdot x - 15} \\[12pt] \end{array}

    Lösung

  • Welche Lösungsmengen haben folgende Logarithmus-Gleichungen?

    \begin{array}{>{\arraybackslash$}p{8cm}<{$} >{\arraybackslash$}p{8cm}<{$}} \text{a) } \log_{\,x}{(125)} = 3 & \text{b) } \log_{5}{(3 \cdot x - 2)} = 4 \\[12pt] \end{array}

    Lösung

Zurück zum Skript