Lineare Gleichungen

Bei einer linearen Gleichung tritt die Variable x nur in der ersten Potenz x^1 auf; sie darf dabei nicht im Nenner stehen. Jede lineare Gleichung kann durch äquivalente Umformungen in die allgemeine Form gebracht werden:

(1)a \cdot x + b = 0

Hierbei sind 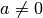a \ne 0 und b beliebige Konstanten.

Um eine beliebige lineare Gleichung zu lösen, werden zunächst durch geeignetes Addieren beziehungsweise Subtrahieren alle die Variable x enthaltenden Terme auf die eine Seite, alle anderen Terme auf die andere Seite der Gleichung gebracht. Auf der Seite der Gleichung, welche die Variable x enthält, kann daraufhin x ausgeklammert und die gesamte Gleichung durch den Restterm geteilt werden. Befindet sich die Gleichung bereits in der allgemeinen Form (1), so kann direkt bestimmt werden:

a \cdot x &= -b \\ \Rightarrow \quad x &= - \frac{b}{a} \\[4pt]

Für die Lösungsmenge einer linearen Gleichung gilt somit \mathbb{L} = \lbrace - \frac{b}{a} \rbrace.

Beispiel:

  • Wie lautet die Lösungsmenge folgender Gleichung?

    \frac{1}{3} \cdot x - 4 = 0 \quad \text{mit } x \in \mathbb{R}

    Um die Gleichung zu lösen, sortiert man alle Variablen (im konkreten Fall alle x-Terme) auf eine Seite der Gleichung, alle Zahlen ohne Variable auf die andere Seite. Dividiert man dann durch den Koeffizienten der Variablen x, so erhält man die Lösung der Gleichung:

    \frac{1}{3} \cdot x &= 4 \\ x &= 12 \\

    Die Lösungsmenge der Gleichung ist somit \mathbb{L} = \{ 12 \}

Hinweis

Zu diesem Abschnitt gibt es Übungsaufgaben.