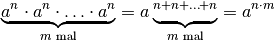Potenzen, Wurzeln und Logarithmen¶
Das Potenzieren entspricht, wie bereits im Abschnitt Rechnen mit reellen Zahlen erwähnt, einem mehrfachen Multiplizieren; das Wurzelziehen hingegen der Umkehrung des Potenzierens. Auf einige der dafür relevanten Rechenregeln wird im folgenden Abschnitt näher eingegangen, ebenso auf das Logarithmieren als zweite Möglichkeit, einen Potenz-Term nach der gesuchten Variablen aufzulösen.
Rechenregeln für Potenzen und Wurzeln¶
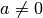 und gleichem Exponent
und gleichem Exponent  lassen sich
somit nach den für reelle Zahlen üblichen Rechenregeln addieren und
subtrahieren.
lassen sich
somit nach den für reelle Zahlen üblichen Rechenregeln addieren und
subtrahieren.(1)¶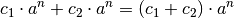
Unterscheiden sich zwei Potenzen in ihrer Basis und/oder in ihrem Exponenten, so kann eine Addition oder Subtraktion beider Potenzen nicht weiter vereinfacht werden. Multiplikationen und Divisionen von Potenzen mit ungleicher Basis und/oder ungleichem Exponenten lassen sich hingegen mit Hilfe der folgenden Rechenregeln umformen.
Rechenregeln für Potenzen mit gleicher Basis
Potenzen können miteinander multipliziert werden, wenn sie eine gemeinsame Basis besitzen. In diesem Fall werden die Exponenten addiert:
(2)¶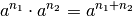
Nach dem gleichen Prinzip können Potenzen mit gleicher Basis dividiert werden, indem man die Differenz ihrer Exponenten bildet:
(3)¶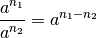
Diese Gleichung erlaubt es, eine Potenz mit negativem Exponenten als Kehrwert
einer Potenz mit positivem Exponenten aufzufassen. Ist nämlich 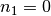 ,
so gilt
,
so gilt 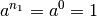 . Damit folgt allgemein:[2]
. Damit folgt allgemein:[2]
(4)¶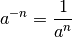
Darüber hinaus gilt für mehrfache Produkte von Potenzen, also für „Potenzen von Potenzen“, folgende Formel[3]:
(5)¶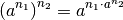
Beispiele:
Multipliziert man
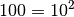 mit
mit 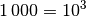 , so lautet das
Ergebnis:
, so lautet das
Ergebnis: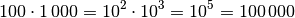
Bei der Multiplikation von Zehnerpotenzen muss somit nur die Anzahl an Nullen addiert werden.
Teilt man
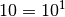 durch
durch 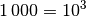 , so lautet das
Ergebnis:
, so lautet das
Ergebnis: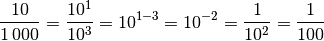
Bei der Division von Zehnerpotenzen wird die Anzahl an Nullen des Nenners von der Anzahl an Nullen des Zählers subtrahiert. Ergibt sich dabei eine negative Anzahl an Nullen, so gibt diese Zahl die Nachkommastelle des Ergebnisses an:
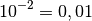
Multipliziert man
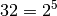 mit sich selbst, so lautet das Ergebnis:
mit sich selbst, so lautet das Ergebnis: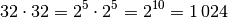
Wird eine Potenz quadriert, so wird ihr Exponent verdoppelt.
Rechenregeln für Potenzen mit gleichen Exponenten
Neben den Rechenregeln für Potenzen mit gleicher Basis können auch Potenzen mit gleichen Exponenten durch Multiplikation bzw. Division zusammengefasst werden.[4] Es gilt:
(6)¶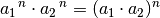
und
(7)¶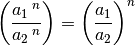
Produkte lassen sich somit potenzieren, indem jeder ihrer Faktoren mit dem gleichen Exponenten potenziert wird. Entsprechend lassen sich auch Brüche potenzieren, indem sowohl Zähler wie auch Nenner den gleichen Exponenten erhalten.
Eine wichtige Rolle hierbei spielt die Potenz 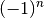 . Je nachdem, ob
. Je nachdem, ob
 geradzahlig (durch
geradzahlig (durch 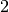 teilbar) ist oder nicht, hebt sich das
Vorzeichen auf bzw. bleibt bestehen:
teilbar) ist oder nicht, hebt sich das
Vorzeichen auf bzw. bleibt bestehen:
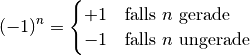
Diese Besonderheit ist mit der Multiplikationsregel „Minus mal Minus gibt Plus“
identisch. Kombiniert man Gleichung
(6) mit der obigen Gleichung,
indem man 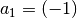 setzt und beide Seiten der Gleichung vertauscht, so
gilt für beliebige Potenzen stets:
setzt und beide Seiten der Gleichung vertauscht, so
gilt für beliebige Potenzen stets:
![(-a)^{2 \cdot n \phantom{+1}} &= (-1)^{2 \cdot n \phantom{+1}} \cdot a^{2
\cdot n \phantom{+1}} = +a^{2 \cdot n} \\[2pt]
(-a)^{2 \cdot n + 1} &= (-1)^{2 \cdot n+1} \cdot a^{2 \cdot n+1} = -a^{2
\cdot n + 1}](../_images/math/f3866541ee716e2f79290eb649c81e86023c4021.png)
Eine negative Basis verliert durch ein Potenzieren mit einem geradzahligen
Exponenten 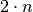 somit stets ihr Vorzeichen. Durch Potenzieren mit
einem ungeradzahligen Exponenten
somit stets ihr Vorzeichen. Durch Potenzieren mit
einem ungeradzahligen Exponenten 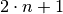 bleibt das Vorzeichen der
Basis hingegen erhalten.
bleibt das Vorzeichen der
Basis hingegen erhalten.
Rechenregeln für Wurzeln und allgemeine Potenzen
Neben der ersten Erweiterung des Potenzbegriffs auf negative Exponenten als logische Konsequenz aus Gleichung (3), die sich auf die Division zweier Potenzen bezieht, ist auch anhand Gleichung (5), die Potenzen von Potenzen beschreibt, eine zweite Erweiterung des Potenzbegriffs möglich. Im Allgemeinen lautet diese Gleichung:
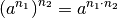
Das Wurzelziehen stellt die Umkehrung des Potenzierens dar. Um die obige
Rechenregel umzukehren, muss die Multiplikation des Exponenten umgekehrt werden.
Setzt man 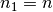 und
und 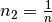 , so
folgt:
, so
folgt:
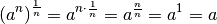
Das Ergebnis stimmt damit überein, dass die  -fache Wurzel einer
-fache Wurzel einer
 -fachen Potenz wieder die ursprüngliche Zahl ergibt:
-fachen Potenz wieder die ursprüngliche Zahl ergibt:
![\sqrt[n]{a^n} = a](../_images/math/dbc1ff3de3fcf63f214009d0849ef8393d2a0182.png)
Tatsächlich können folgende Umformungen als allgemeine Rechenregeln genutzt werden:
(8)¶![\sqrt[n]{a} = a^{\frac{1}{n}}](../_images/math/549ba4b65a7cc2b141bb2785e1c804ca084cf48f.png)
sowie
(9)¶![\sqrt[n_2]{a^{n_1}} = a^{\frac{n_1}{n_2}}](../_images/math/d9a458deecea29ea3853a386b8ce18a8ed9ea855.png)
Da Wurzeln somit nichts anderes als Potenzen mit gebrochenem Exponenten 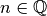 darstellen, gelten die in den beiden vorherigen Abschnitten
aufgeführten Rechenregeln (1) bis
(7) gleichermaßen auch für Wurzeln.
darstellen, gelten die in den beiden vorherigen Abschnitten
aufgeführten Rechenregeln (1) bis
(7) gleichermaßen auch für Wurzeln.
Auf Wurzelgleichungen wird im Rahmen der elementaren Algebra, auf Wurzelfunktionen im Analysis-Kapitel näher eingegangen.
Rechenregeln für Logarithmen¶
Das Logarithmieren stellt neben dem Wurzelziehen eine zweite Möglichkeit dar,
eine Potenz 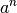 zu finden, die ein bestimmtes Ergebnis
zu finden, die ein bestimmtes Ergebnis  liefert. Während beim Wurzelziehen der (Wurzel-)Exponent
liefert. Während beim Wurzelziehen der (Wurzel-)Exponent  vorgegeben
ist und die zum Wert der Potenz passende Basis
vorgegeben
ist und die zum Wert der Potenz passende Basis  gesucht wird, hilft das
Logarithmieren dabei, den zu einer vorgegebenen Basis
gesucht wird, hilft das
Logarithmieren dabei, den zu einer vorgegebenen Basis  passenden
Exponenten
passenden
Exponenten  zu finden. Die Fragestellung lautet somit:
zu finden. Die Fragestellung lautet somit:
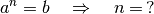
Um dieses mathematische Problem zu lösen, muss der so genannte Logarithmus
von  zur Basis
zur Basis  ermittelt werden.
ermittelt werden.
Definition:
Der Logarithmus
ist diejenige Zahl, mit welcher die Basis
potenziert werden muss, um das Ergebnis
zu erhalten. Es gilt:
Beispielsweise gilt somit 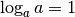 , wie sich durch Einsetzen in
den linken Teil der obigen Äquivalenz-Gleichung überprüfen lässt, sowie
, wie sich durch Einsetzen in
den linken Teil der obigen Äquivalenz-Gleichung überprüfen lässt, sowie
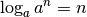 , da
, da  genau der Zahl entspricht, mit der die
Basis
genau der Zahl entspricht, mit der die
Basis  potenziert werden muss, um das Ergebnis
potenziert werden muss, um das Ergebnis 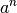 zu erhalten.
zu erhalten.
Eine einfache Berechnung eines Logarithmus „von Hand“ ist allgemein nur in seltenen Fällen möglich. Früher wurden daher Werte-Tabellen für Logarithmen in Lehrbüchern und Formelsammlungen abgedruckt, inzwischen haben Taschenrechner bzw. Computerprogramme mit entsprechenden Funktionen die Berechnung von Logarithmen wesentlich vereinfacht und Werte-Tabellen letztlich überflüssig gemacht.
In der Praxis sind insbesondere Logarithmen zur Basis 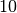 („dekadische“
Logarithmen, Symbol:
(„dekadische“
Logarithmen, Symbol: 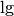 ), zur Basis
), zur Basis  („natürliche“
Logarithmen, Symbol:
(„natürliche“
Logarithmen, Symbol: 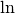 ) und zur Basis
) und zur Basis 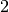 („binäre“ oder
duale“ Logarithmen, Zeichen
(„binäre“ oder
duale“ Logarithmen, Zeichen 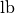 oder
oder 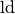 ) von
Bedeutung.[5] Um einen Logarithmus auf eine andere Basis umzurechnen, kann
folgende Formel angewendet werden:
) von
Bedeutung.[5] Um einen Logarithmus auf eine andere Basis umzurechnen, kann
folgende Formel angewendet werden:
(10)¶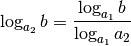
Die obige Formel ermöglicht es beispielsweise, einen dekadischen Logarithmus
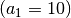 in einen binären Logarithmus
in einen binären Logarithmus 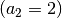 umzurechnen,
indem man diesen durch
umzurechnen,
indem man diesen durch 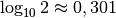 teilt.
teilt.
Summen und Differenzen von Logarithmen
Logarithmen mit gleicher Basis lassen sich addieren oder subtrahieren. Das Ergebnis einer Logarithmus-Addition ist ein Logarithmus mit gleicher Basis, dessen Argument gleich dem Produkt der Argumente beider zu addierenden Logarithmen ist:
(11)¶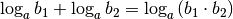
Entsprechend ist das Ergebnis einer Logarithmus-Subtraktion ein Logarithmus mit gleicher Basis, dessen Argument gleich dem Quotienten der Argumente beider zu subtrahierender Logarithmen ist:
(12)¶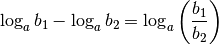
Wird ein Logarithmus mit einem konstanten Faktor  multipliziert, so
entspricht dies einer
multipliziert, so
entspricht dies einer  -Fachen Addition des Logarithmus mit sich selbst.
In diesem Fall entspricht das Ergebnis somit einem Logarithmus mit gleicher Basis
-Fachen Addition des Logarithmus mit sich selbst.
In diesem Fall entspricht das Ergebnis somit einem Logarithmus mit gleicher Basis
 , dessen Argument
, dessen Argument  -fach mit sich selbst multipliziert werden
muss:
-fach mit sich selbst multipliziert werden
muss:
(13)¶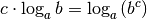
Auf Logarithmusgleichungen wird im Rahmen der elementaren Algebra, auf Logarithmusfunktionen im Analysis-Kapitel näher eingegangen.
Anmerkungen:
| [1] | Auch allgemeine Potenzen (mit beliebigem Exponenten 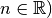 lassen sich auf diese Art addieren bzw. subtrahieren.
Die Einschränkung lassen sich auf diese Art addieren bzw. subtrahieren.
Die Einschränkung 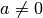 ist dabei notwendig, da die
Potenz ist dabei notwendig, da die
Potenz 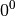 nicht definiert ist. nicht definiert ist. |
| [2] | Auf diese Weise lässt sich eine plausible Erklärung angeben, warum
|
| [3] | Die Gleichung für Potenzen von Potenzen folgt aus der Gleichung für
Potenz-Multiplikationen. Setzt man in Gleichung
(2) für
|
| [4] | Additionen und Subtraktionen von Potenzen mit ungleicher Basis lassen sich nicht weiter zusammenfassen. |
| [5] | Für dekadische Logarithmen 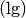 und natürliche
Logarithmen und natürliche
Logarithmen 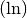 besitzen Taschenrechner häufig
entsprechende Funktionstasten. besitzen Taschenrechner häufig
entsprechende Funktionstasten. |
Hinweis
Zu diesem Abschnitt gibt es Übungsaufgaben.

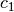 und
und 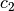 für beliebige konstante
Zahlen und
für beliebige konstante
Zahlen und 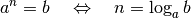
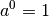 für alle
für alle 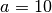
![10^{-3} &= \frac{1}{1\,000} = 0,001 \\[2pt]
10^{-2} &= \frac{1}{\phantom{\,}100\phantom{0}} = 0,01 \\[2pt]
10^{-1} &= \frac{1}{\phantom{\,\,\,}10\phantom{\,\,\,\,}} = 0,1 \\[2pt]
10^{\pm0} &= \frac{1}{\phantom{0\,\,}1\phantom{0\,\,}} = 1 \\[2pt]
10^{+1} &= \frac{\phantom{\,\,\,}10\phantom{\,\,\,\,}}{1} = 10 \\[2pt]
10^{+2} &= \frac{\phantom{\,}100\phantom{0}}{1} = 100 \\[2pt]
10^{+3} &= \frac{1\,000}{1} = 1\,000](../_images/math/fdffcf3202db9241b81df0f12aabe832baee4a2a.png)
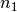 und
und 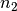 gleiche
Werte ein, d.h.
gleiche
Werte ein, d.h. 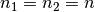 , so gilt:
, so gilt: