Potenz- und Wurzelfunktionen¶
Eine Potenzfunktion hat allgemein folgende Funktionsgleichung:
(1)¶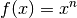
In praktischen Anwendungen treten Potenzfunktionen sehr häufig auf;
beispielsweise werden durch sie Proportionalitäten zwischen einer Größe
 und der
und der  -ten Potenz der Ausgangsgröße
-ten Potenz der Ausgangsgröße  beschrieben.
Wichtige Sonderfälle sind hierbei mit
beschrieben.
Wichtige Sonderfälle sind hierbei mit 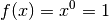 die konstante
Funktion und mit
die konstante
Funktion und mit 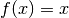 die lineare Funktion. Wurzelfunktionen lassen
sich ebenfalls als Potenzfunktion mit rationalem Exponenten auffassen.
die lineare Funktion. Wurzelfunktionen lassen
sich ebenfalls als Potenzfunktion mit rationalem Exponenten auffassen.
Einige wichtige Eigenschaften von Potenzfunktionen werden im Folgenden näher beschrieben.
Gerade und ungerade Potenzfunktionen¶
Potenzfunktionen auch höheren Grades – also allgemein Funktionen der Form
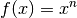 mit
mit 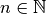 – lassen sich in gerade und
ungerade Funktionen unterteilen.
– lassen sich in gerade und
ungerade Funktionen unterteilen.
Potenzfunktionen mit geraden Exponenten
Eine Funktion heißt „gerade“, wenn für alle 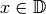 folgende
Bedingung gilt:
folgende
Bedingung gilt:
(2)¶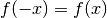
Zu jedem Punkt des Funktionsgraphen existiert in diesem Fall ein zweiter
Kurvenpunkt, der achsensymmetrisch zur  -Achse ist. Diese Bedingung
wird von allen Potenzfunktionen mit geradzahligen Exponenten erfüllt, da sich
bei diesen die Minuszeichen der negativen
-Achse ist. Diese Bedingung
wird von allen Potenzfunktionen mit geradzahligen Exponenten erfüllt, da sich
bei diesen die Minuszeichen der negativen  -Werte beim Potenzieren
gegenseitig aufheben. Die konstante Funktion
-Werte beim Potenzieren
gegenseitig aufheben. Die konstante Funktion 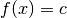 wird ebenfalls zu
den geraden Funktionen gezählt, da
wird ebenfalls zu
den geraden Funktionen gezählt, da 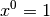 ist.
ist.
Zusätzlich haben alle geraden Potenzfunktionen folgende Eigenschaften:
- Die Funktionsgraphen verlaufen stets durch die Punkte
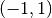 ,
,
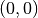 und
und 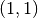 .
. - Die Funktionen sind streng monoton fallend für
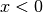 und streng monoton
steigend für
und streng monoton
steigend für 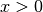 .[1]
.[1] - Der Definitionsbereich der Funktionen ist
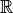 , ihr Wertebereich
, ihr Wertebereich
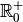 ; sie sind also nach unten beschränkt, und für die untere
Schranke gilt
; sie sind also nach unten beschränkt, und für die untere
Schranke gilt 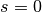 .
.
Potenzfunktionen mit ungeraden Exponenten
Eine Funktion heißt „ungerade“, wenn für alle 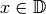 folgende Bedingung gilt:
folgende Bedingung gilt:
(3)¶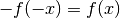
Zu jedem Punkt des Funktionsgraphen existiert somit ein zweiter Kurvenpunkt,
der punktsymmetrisch zum Koordinatenursprung 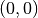 ist. Diese
Bedingung wird von allen Potenzfunktionen mit ungeraden Exponenten erfüllt,
da sich die Funktionswerte von negativen
ist. Diese
Bedingung wird von allen Potenzfunktionen mit ungeraden Exponenten erfüllt,
da sich die Funktionswerte von negativen  -Werte gegenüber den
Funktionswerten von betragsgleichen positiven
-Werte gegenüber den
Funktionswerten von betragsgleichen positiven  -Werten nur im
Vorzeichen unterscheiden.[2]
-Werten nur im
Vorzeichen unterscheiden.[2]
Zusätzlich haben alle ungeraden Potenzfunktionen folgende Eigenschaften:
- Der Funktionsgraph verläuft stets durch die Punkte
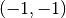 ,
,
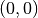 und
und 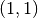 .
. - Die Funktion ist für alle
 -Werte entweder streng monoton fallend oder streng monoton
steigend.
-Werte entweder streng monoton fallend oder streng monoton
steigend. - Der Definitionsbereich sowie der Wertebereich der Funktion ist
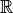 .
.
Wurzelfunktionen¶
Wurzelfunktionen haben allgemein folgende Funktionsgleichung:
(4)¶![f(x) = \sqrt[n]{x}](../../_images/math/865d1012b9bf5ef1990314b38339b22776c4178e.png)
Dabei ist der Wurzelexponent  eine feste natürliche und die Variable
eine feste natürliche und die Variable
 eine beliebige positive reelle Zahl.[3] Da die Wurzel einer beliebigen
positiven Zahl ebenfalls eine positive Zahl ist, ist
eine beliebige positive reelle Zahl.[3] Da die Wurzel einer beliebigen
positiven Zahl ebenfalls eine positive Zahl ist, ist 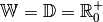 .
Aufgrund der Beziehung
.
Aufgrund der Beziehung ![\sqrt[n]{x} = x ^{\frac{1}{n}}](../../_images/math/b0064f314df345c654291cc30afec0fed196b7b6.png) lassen sich
Wurzelfunktionen als Potenzfunktionen mit rationalem Exponenten auffassen.
Zugleich ist die
lassen sich
Wurzelfunktionen als Potenzfunktionen mit rationalem Exponenten auffassen.
Zugleich ist die  -te Wurzelfunktion
-te Wurzelfunktion ![y=\sqrt[n]{x}](../../_images/math/be2000266074c87183bce204b089a5e342fb188b.png) die
Umkehrfunktion der
die
Umkehrfunktion der  -ten Potenzfunktion
-ten Potenzfunktion 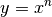 , da gilt:
, da gilt:
![x = f_{\mathrm{U}}(y) = \sqrt[n]{x^n} = x ^{\frac{n}{n}} = x^1 = x](../../_images/math/af6d6f4320d5219d2b5182be74916e605377fd1a.png)
Alle Wurzelfunktionen sind stetig, streng monoton steigend und haben 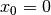 als (einfache) Nullstelle. Die Funktionsgraphen haben neben dem Punkt
als (einfache) Nullstelle. Die Funktionsgraphen haben neben dem Punkt
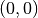 auch den Punkt
auch den Punkt 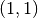 gemeinsam; sie entstehen durch
Spiegelung der jeweiligen Potenzfunktion
gemeinsam; sie entstehen durch
Spiegelung der jeweiligen Potenzfunktion 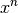 an der Geraden
an der Geraden 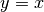 .
.
Anmerkungen:
| [1] | Steht eine Potenzfunktion in Betragszeichen, ist also 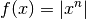 , so ist diese Funktion in jedem Fall gerade, da mögliche negative
Vorzeichen von Funktionswerten dadurch aufgehoben werden (siehe
beispielsweise Abbildung Betragsfunktion). , so ist diese Funktion in jedem Fall gerade, da mögliche negative
Vorzeichen von Funktionswerten dadurch aufgehoben werden (siehe
beispielsweise Abbildung Betragsfunktion). |
| [2] | Um die Umkehrfunktion einer geraden Potenzfunktion zu bilden, muss somit
der Definitionsbereich eingeschränkt werden (meist auf 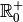 ). ). |
| [3] | Diese Einschränkung ist zumindest für reellwertige Funktionen
notwendig, da in diesem Fall keine Wurzeln mit negativen Argumenten
definiert sind.
Im Bereich der komplexen Zahlen
gilt die Beziehung
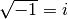 . . |



