Ganz- und gebrochenrationale Funktionen¶
Ganzrationale Funktionen¶
Ganzrationale Funktionen haben allgemein folgende Funktionsgleichung:
(1)¶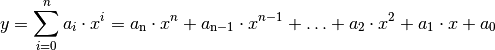
Hierbei bezeichnet man den größten Exponenten 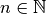 des
Polynoms als „Grad“ der Funktion, die reellen Zahlen
des
Polynoms als „Grad“ der Funktion, die reellen Zahlen 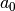 bis
bis 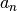 nennt man Koeffizienten. Ganzrationale Funktionen haben allgemein folgende
Eigenschaften:
nennt man Koeffizienten. Ganzrationale Funktionen haben allgemein folgende
Eigenschaften:
Ganzrationale Funktionen sind für alle reellen Zahlen definiert, es gilt also
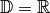 . Sie sind im gesamten Bereich stetig, der
Funktionsgraph ergibt also eine kontinuierliche Kurve ohne Sprünge („glatt,
aber meist wellig“).
. Sie sind im gesamten Bereich stetig, der
Funktionsgraph ergibt also eine kontinuierliche Kurve ohne Sprünge („glatt,
aber meist wellig“).Jede Potenzfunktion
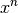 mit
mit 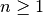 wird für große
wird für große
 -Werte unendlich groß, da
-Werte unendlich groß, da 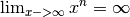 ist. Bei einer ganzrationalen Funktion richtet sich der Grenzwert nach der
höchsten Potenz und hat das gleiche Vorzeichen wie der dazugehörige
Koeffizient.
ist. Bei einer ganzrationalen Funktion richtet sich der Grenzwert nach der
höchsten Potenz und hat das gleiche Vorzeichen wie der dazugehörige
Koeffizient.Jede ganzrationale Funktion
 -ten Grades hat maximal
-ten Grades hat maximal  verschiedene Nullstellen.
verschiedene Nullstellen.Ebenso ist es möglich, dass bei der Bestimmung der Nullstellen ein Wert mehrfach vorkommt. In diesem Fall ist die Nullstelle mehrfach zu zählen, wobei der Vielfachheit folgende Bedeutung zukommt:
- Bei geradzahlig-mehrfachen Nullstellen berührt der Funktionsgraph die
 -Achse, verbleibt allerdings auf der selben Seite der Achse.
-Achse, verbleibt allerdings auf der selben Seite der Achse. - Bei ungeradzahlig-mehrfachen Nullstellen schneidet der Funktionsgraph die
 -Achse.
-Achse.
- Bei geradzahlig-mehrfachen Nullstellen berührt der Funktionsgraph die
Aus Potenzfunktionen zusammengesetzte Funktionen sind meist weder gerade noch
ungerade, außer sie bestehen ausschließlich aus nur geraden oder nur ungeraden
Potenzfunktionen. Sowohl gerade als auch ungerade Funktionen haben besondere
Stellen 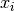 (Nullstellen, Extremstellen und Wendepunkte), sofern
(Nullstellen, Extremstellen und Wendepunkte), sofern
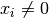 ist, stets paarweise. Die
ist, stets paarweise. Die  -Werte der besonderen
Stellen unterscheiden sich dabei nur in ihrem Vorzeichen, es ist also
-Werte der besonderen
Stellen unterscheiden sich dabei nur in ihrem Vorzeichen, es ist also 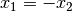 . Zudem haben sie folgende Eigenschaften:
. Zudem haben sie folgende Eigenschaften:
- Ganzrationale Funktionen geraden Grades sind stets einseitig beschränkte Funktionen. Sie haben entweder keine oder eine gerade Anzahl an Nullstellen, die unter Umständen mehrfach zu zählen sind.
- Ganzrationale Funktionen ungeraden Grades sind stets unbeschränkt und haben stets (mindestens) eine Nullstelle. Die Gesamtzahl der Nullstellen ist stets ungerade.
Im Folgenden werden die obigen und weitere Eigenschaften am Beispiel der häufig
vorkommenden linearen und quadratischen Funktionen, also den einfachsten
Vertretern von ganzrationalen Funktionen (mit 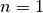 beziehungsweise
beziehungsweise
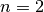 ), näher beschrieben.
), näher beschrieben.
Lineare Funktionen¶
Wenn eine Größe in gleichem Maß zunimmt wie auch eine andere Größe wächst, so nennt man den Zusammenhang direkt proportional oder linear. Die zugehörige mathematische Funktion hat folgende Form:
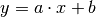
Lineare Zusammenhänge zweier Größen treten im Alltag – beispielsweise bei Dreisatz-Aufgaben – sowie in den Naturwissenschaften sehr häufig auf.
Beispiele:
- Je größer die Geschwindigkeit eines Fahrzeugs ist, desto länger ist die Wegstrecke, die es in einer bestimmten Zeit zurücklegt.
- Je mehr Plätzchen auf Vorrat gebacken werden, desto länger kann man davon naschen (vorausgesetzt, jeden Tag werden gleich viele Plätzchen verspeist).
- Je mehr Geld man ausgeben möchte, desto mehr muss man verdienen. Oder: Je sparsamer man mit einer bestimmten Menge Geld umgeht, desto länger kann man davon leben. Ähnlich ist es mit dem Benzinverbrauch eines Fahrzeugs.
Der Graph einer linearen Funktion ist eine Gerade, die umso steiler verläuft, je
größer der Proportionalitätsfaktor  ist;
ist;  wird daher auch aus
„Steigung“ der linearen Funktion bezeichnet. Der Wert
wird daher auch aus
„Steigung“ der linearen Funktion bezeichnet. Der Wert  stellt den
Anfangswert dar (das Ergebnis der Funktion, wenn
stellt den
Anfangswert dar (das Ergebnis der Funktion, wenn 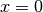 ist).
ist).

Graphen der linearen Funktionen 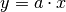 beziehungsweise
beziehungsweise
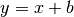 mit unterschiedlichen Parametern
mit unterschiedlichen Parametern  (links) und
(links) und
 (rechts).
(rechts).
Eine Funktion heißt proportional, wenn das Verhältnis der Größen
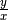 immer einen konstanten Wert hat, wenn also
immer einen konstanten Wert hat, wenn also
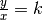 gilt. Das ist genau dann der Fall, wenn
gilt. Das ist genau dann der Fall, wenn 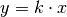 ist. Bei proportionalen Funktionen handelt es sich folglich um lineare
Funktionen, die üblicherweise durch den Koordinatenursprung verlaufen und eine
positive Steigung aufweisen.
ist. Bei proportionalen Funktionen handelt es sich folglich um lineare
Funktionen, die üblicherweise durch den Koordinatenursprung verlaufen und eine
positive Steigung aufweisen.
Quadratische Funktionen¶
In manchen Situationen wächst eine Größe durch den Einfluss einer anderen Größe
stärker als proportional. Nimmt eine Messgröße um das 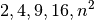 -fache
zu, während die Ausgangsgröße den
-fache
zu, während die Ausgangsgröße den 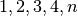 -fachen Wert annimmt, so
nennt man die zugehörige Funktion quadratisch.
-fachen Wert annimmt, so
nennt man die zugehörige Funktion quadratisch.
Beispiele:
Ein Quadrat mit einer
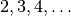 -fachen Seitenlänge
-fachen Seitenlänge 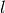 besitzt einen
besitzt einen
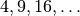 -fachen Flächeninhalt
-fachen Flächeninhalt 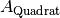 .
.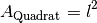
Die Fläche
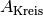 eines Kreises wächst ebenfalls
quadratisch mit zunehmendem Radius an. Zur exakten Berechnung muss der Radius
eines Kreises wächst ebenfalls
quadratisch mit zunehmendem Radius an. Zur exakten Berechnung muss der Radius
 quadriert und mit der Kreiszahl
quadriert und mit der Kreiszahl 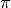 multipliziert werden.
multipliziert werden.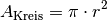
Die Strecke, die ein Körper im freien Fall (ohne Reibung) zurücklegt, nimmt quadratisch mit der Zeit zu: Nach einer Sekunde hat der Körper knapp 5 Meter zurückgelegt, nach zwei Sekunden 20 Meter, nach drei Sekunden 45 Meter, nach vier Sekunden 80 Meter, usw. Allgemein gilt für die Fallstrecke
 mit
der Erdbeschleunigung
mit
der Erdbeschleunigung ![g = \unit[9,81]{\frac{m}{s^2} }](../../_images/math/ca836dd38a81dc76f1c11f3a529255a8bba5a61f.png) folgende Formel:
folgende Formel: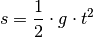
Der Graph einer quadratischen Funktion ist eine Parabel beziehungsweise ein Stück davon.
Die Normalparabel
Allgemein besitzt eine quadratische Funktion folgende Form:
(2)¶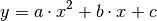
Im einfachsten Fall sind die beiden Parameter 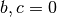 sowie
sowie 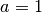 . Die Funktion vereinfacht sich damit zu:
. Die Funktion vereinfacht sich damit zu:
(3)¶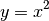
Den zu Gleichung (3) gehörigen Funktionsgraphen nennt man
Normalparabel. Ihre Funktionswerte ergeben sich jeweils durch Quadrieren der
eingesetzten  -Werte.
-Werte.
Die Besonderheiten einer Normalparabel sind:
- Der Scheitel der Normalparabel liegt bei
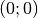 .
. - Die Normalparabel ist symmetrisch zur
 -Achse. Der Grund hierfür ist,
dass sich das Minuszeichen beim Quadrieren aufhebt – Minus mal Minus ergibt
Plus.
-Achse. Der Grund hierfür ist,
dass sich das Minuszeichen beim Quadrieren aufhebt – Minus mal Minus ergibt
Plus. - Die Normalparabel besitzt nur nicht-negative
 -Werte, sie bildet also
den Definitionsbereich
-Werte, sie bildet also
den Definitionsbereich 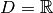 auf den positiven Bereich der
reellen Zahlen
auf den positiven Bereich der
reellen Zahlen 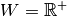 ab. Der Grund hierfür ist, dass für
die Quadratzahl einer jeden reellen Zahl
ab. Der Grund hierfür ist, dass für
die Quadratzahl einer jeden reellen Zahl 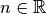 gilt:
gilt:
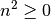
Bedeutung der Parameter 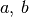 und
und 
Durch Variation der Parameterwerte 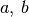 und
und  ergeben sich
gegenüber der Normalparabel folgende Veränderungen:
ergeben sich
gegenüber der Normalparabel folgende Veränderungen:
Ist der Parameter
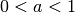 , so ist die Parabel gegenüber der
Normalparabel gestaucht, ihre Werte wachsen also langsamer als es bei der
Normalparabel der Fall ist. Im umgekehrten Fall
, so ist die Parabel gegenüber der
Normalparabel gestaucht, ihre Werte wachsen also langsamer als es bei der
Normalparabel der Fall ist. Im umgekehrten Fall 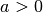 ist die
resultierende Parabel gegenüber der Normalparabel gestreckt.
ist die
resultierende Parabel gegenüber der Normalparabel gestreckt.Gilt
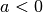 , so ist die Parabel nach unten hin geöffnet.
, so ist die Parabel nach unten hin geöffnet.
Lässt sich eine Parabelgleichung als binomische Formel schreiben, beispielsweise
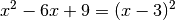 oder allgemein
oder allgemein 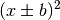 , so bewirkt der in der quadrierten Klammer stehende Parameter
, so bewirkt der in der quadrierten Klammer stehende Parameter  eine Verschiebung nach links (falls
eine Verschiebung nach links (falls 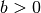 ) beziehungsweise nach rechts
(falls
) beziehungsweise nach rechts
(falls 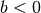 ).
).Die Wirkung des Parameters
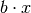 lässt sich bestimmen, indem man
mit Hilfe der ersten Ableitung den Wert des Parabelscheitels allgemein
berechnet.[1] Je nach Größe der Werte von
lässt sich bestimmen, indem man
mit Hilfe der ersten Ableitung den Wert des Parabelscheitels allgemein
berechnet.[1] Je nach Größe der Werte von  und
und  bewirkt
der Parameter
bewirkt
der Parameter  eine Verschiebung des Parabelscheitels um
eine Verschiebung des Parabelscheitels um 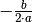 in horizontaler und um
in horizontaler und um 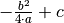 in vertikaler Richtung. Im Falle einer Normalparabel (
in vertikaler Richtung. Im Falle einer Normalparabel (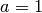 und
und
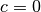 ) bewirkt
) bewirkt 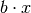 eine Verschiebung um
eine Verschiebung um 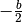 in
in  -Richtung sowie eine Verschiebung um
-Richtung sowie eine Verschiebung um 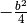 in
in  -Richtung.
-Richtung.
- Ist der Parameter
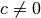 , so ist die Parabel nach oben (
, so ist die Parabel nach oben (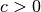 ) beziehungsweise nach unten (
) beziehungsweise nach unten (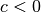 ) verschoben.
) verschoben.
Treten mehrere der oben genannten Fälle ein, so kombinieren sich entsprechend die Effekte.
Gebrochenrationale Funktionen¶
Gebrochenrationale Funktionen haben allgemein folgende Funktionsgleichung:
(4)¶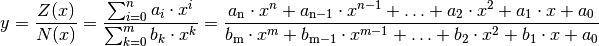
Gebrochenrationale Funktionen bestehen also aus einem Zählerpolynom
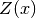 mit Grad
mit Grad  und einem Nennerpolynom
und einem Nennerpolynom 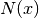 mit Grad
mit Grad
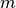 . Ist
. Ist 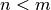 , so nennt man die Funktion „echt“ gebrochenrational;
andernfalls lässt sich die Funktion mittels Polynomdivision als Summe einer ganzrationalen Funktion und einer echt
gebrochenrationalen Funktion schreiben.
, so nennt man die Funktion „echt“ gebrochenrational;
andernfalls lässt sich die Funktion mittels Polynomdivision als Summe einer ganzrationalen Funktion und einer echt
gebrochenrationalen Funktion schreiben.
Nullstellen und Polstellen¶
Gebrochenrationale Funktionen sollten stets auf folgende Punkte hin untersucht werden:
- Als Nullstellen von gebrochenrationalen Funktionen werden alle
 -Werte
bezeichnet, für die der Zählerterm
-Werte
bezeichnet, für die der Zählerterm 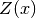 gleich Null wird, ohne dass
der Nennerterm
gleich Null wird, ohne dass
der Nennerterm 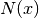 ebenfalls gleich Null wird.
ebenfalls gleich Null wird. - Als Polstellen von gebrochenrationalen Funktionen werden alle
 -Werte
bezeichnet, für die der Nennerterm
-Werte
bezeichnet, für die der Nennerterm 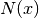 gleich Null wird, ohne dass
der der Zählerterm
gleich Null wird, ohne dass
der der Zählerterm 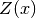 ebenfalls gleich Null wird. Die Funktion ist
(wegen der Division durch Null) an solchen Stellen nicht definiert. Der
Graph der Funktion ist an Polstellen nicht stetig, sondern nähert sich
asymptotisch einer durch entsprechenden
ebenfalls gleich Null wird. Die Funktion ist
(wegen der Division durch Null) an solchen Stellen nicht definiert. Der
Graph der Funktion ist an Polstellen nicht stetig, sondern nähert sich
asymptotisch einer durch entsprechenden  -Wert verlaufenden und zur
-Wert verlaufenden und zur
 -Achse parallelen Geraden an.[2]
-Achse parallelen Geraden an.[2]
Beispiel:
Die folgende Funktion soll auf Nullstellen und Polstellen hin untersucht werden:
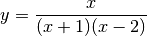
Der Zählerterm ist nur für
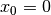 gleich Null, der Funktionsgraph
hat somit nur dort eine Nullstelle. Um die Polstelle(n) zu bestimmen, muss der
Nennerterm gleich Null gesetzt werden:
gleich Null, der Funktionsgraph
hat somit nur dort eine Nullstelle. Um die Polstelle(n) zu bestimmen, muss der
Nennerterm gleich Null gesetzt werden:![(x+1) \cdot (x-2) \stackrel{!}= 0 \\[6pt]
\Rightarrow x_1 = -1 \quad ; \quad x_2 = +2](../../_images/math/aefa1ba8dc67b3217ce8db5e0a786aaacf522bf3.png)
Die Funktion hat also zwei Polstellen bei
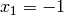 und
und 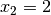 .
.
Werden sowohl der Zählerterm 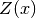 als auch der Nennerterm
als auch der Nennerterm 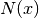 für einen Wert
für einen Wert 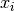 gleich Null, so ist die Funktion an dieser Stelle
ebenfalls nicht definiert. Zähler und Nenner enthalten jedoch in diesem Fall
einen gemeinsamen Faktor
gleich Null, so ist die Funktion an dieser Stelle
ebenfalls nicht definiert. Zähler und Nenner enthalten jedoch in diesem Fall
einen gemeinsamen Faktor 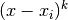 , durch den der gebrochenrationale
Term für
, durch den der gebrochenrationale
Term für 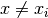 gekürzt werden kann.
gekürzt werden kann.
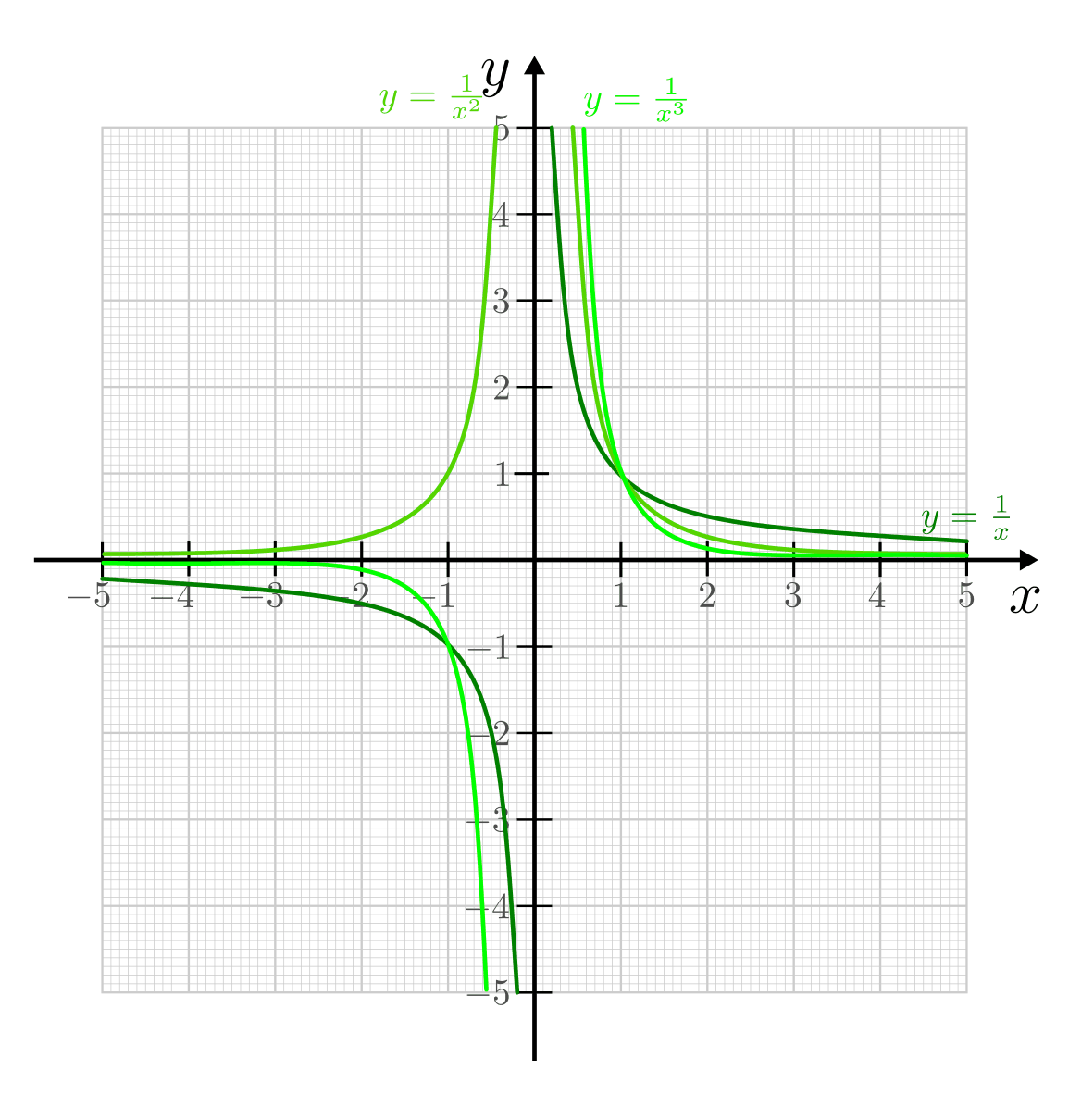
Hyperbeln¶
Funktionen der Form 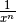 stellen die einfachsten
gebrochenrationalen Funktionen dar; sie werden Hyperbeln genannt. Alle diese
Funktionen haben bei
stellen die einfachsten
gebrochenrationalen Funktionen dar; sie werden Hyperbeln genannt. Alle diese
Funktionen haben bei 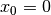 eine Polstelle, die
eine Polstelle, die  -Achse ist
also eine senkrechte Asymptote. Die zweite, waagrechte Asymptote der Funktion
für
-Achse ist
also eine senkrechte Asymptote. Die zweite, waagrechte Asymptote der Funktion
für 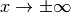 ist die
ist die  -Achse.
-Achse.
Alle Hyperbeln haben, da der Zähler stets ungleich Null ist, keine
Nullstellen. Zudem verlaufen die Funktionsgraphen aller Hyperbeln durch den
Punkt 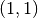 .
Aufgrund der Beziehung
.
Aufgrund der Beziehung 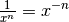 lassen sich
Hyperbelfunktionen als Potenzfunktionen mit negativen Exponenten auffassen.
Damit können auch Hyperbeln in gerade und ungerade Funktionen unterteilt werden:
lassen sich
Hyperbelfunktionen als Potenzfunktionen mit negativen Exponenten auffassen.
Damit können auch Hyperbeln in gerade und ungerade Funktionen unterteilt werden:
- Die Funktionsgraphen von Hyperbeln mit geraden Exponenten sind
achsensymmetrisch zur
 -Achse, sie verlaufen also im ersten und
zweiten Quadranten und gehen zusätzlich durch den Punkt
-Achse, sie verlaufen also im ersten und
zweiten Quadranten und gehen zusätzlich durch den Punkt 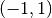 .
Im Bereich
.
Im Bereich 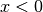 sind gerade Hyperbeln streng monoton steigend, im
Bereich
sind gerade Hyperbeln streng monoton steigend, im
Bereich 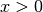 streng monoton fallend. Nach unten sind gerade Hyperbeln
mit der unteren Schranke
streng monoton fallend. Nach unten sind gerade Hyperbeln
mit der unteren Schranke 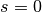 beschränkt.
beschränkt. - Die Funktionsgraphen von Hyperbeln mit ungeraden Exponenten sind
punktsymmetrisch zum Koordinatenursprung
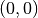 , sie verlaufen also im
ersten und dritten Quadranten und gehen zusätzlich durch den Punkt
, sie verlaufen also im
ersten und dritten Quadranten und gehen zusätzlich durch den Punkt
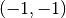 . Im gesamten Definitionsbereich sind ungerade Hyperbeln streng
monoton steigend.
. Im gesamten Definitionsbereich sind ungerade Hyperbeln streng
monoton steigend.
Aufgrund der Beziehung 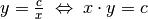 können mit Hyperbeln indirekte Proportionalitäten zwischen
können mit Hyperbeln indirekte Proportionalitäten zwischen  und
und  beschrieben werden.
beschrieben werden.
Anmerkungen:
| [1] | Für die erste Ableitung der Parabelgleichung (2) gilt:
Der Parabelscheitel ist die einzige Stelle einer Parabel, an der ihre
Steigung
Den zugehörigen
|
| [2] | Als Asymptote bezeichnet man allgemein eine Gerade oder Kurve, an die sich eine Funktion an einer Polstelle oder im Unendlichen annähert. Bei einer gebrochenrationalen Funktion erhält man für Ist der Grad des Zählers gleich dem Grad des Nenners, so hat die
gebrochenrationale Funktion für |


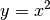 .
.
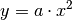 für verschiedene
Parameter
für verschiedene
Parameter 
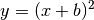 beziehungsweise
beziehungsweise 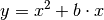 für verschiedene Parameter
für verschiedene Parameter 
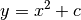 für verschiedene
Parameter
für verschiedene
Parameter 
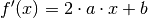
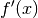 gleich Null ist (Extremwert). Der
gleich Null ist (Extremwert). Der 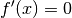 gesetzt wird:
gesetzt wird:![f'(x) = 0 \quad &\Leftrightarrow \quad 2 \cdot a \cdot x + b = 0 \\[6pt]
&\Rightarrow x = - \frac{b}{2 \cdot a}](../../_images/math/425f178bf98e514564b1556288f2f202fc623afb.png)
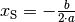 in die ursprüngliche
Parabelgleichung
in die ursprüngliche
Parabelgleichung ![y_{\mathrm{S}} = f\left(-\frac{b}{2 \cdot a}\right) &= a \cdot \left( -
\frac{b}{2 \cdot a} \right)^2 + b \cdot \left( - \frac{b}{2 \cdot
a} \right) + c \\[6pt]
&= a \cdot \frac{b^2}{4 \cdot a^2} - \frac{b^2}{2 \cdot a} + c \\[6pt]
&= \frac{b^2}{4 \cdot a} - \frac{2 \cdot b^2}{4 \cdot a} + c \\[6pt]
&= - \frac{b^2}{4 \cdot a} + c](../../_images/math/3f7e4a47efa51485cb827d36448a37e29a4669fa.png)
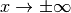 eine schräg verlaufende Gerade als Asymptote, wenn der Grad des
Zählers um
eine schräg verlaufende Gerade als Asymptote, wenn der Grad des
Zählers um 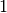 größer ist als der Grad des Nenners. Ist der Grad
des Zählers um
größer ist als der Grad des Nenners. Ist der Grad
des Zählers um 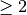 größer als der Grad des Nenners, so nähert
sich die gebrochenrationale Funktion asymptotisch an eine schräge Kurve an.
In beiden Fällen kann die Funktionsgleichung der Asymptote mittels einer
größer als der Grad des Nenners, so nähert
sich die gebrochenrationale Funktion asymptotisch an eine schräge Kurve an.
In beiden Fällen kann die Funktionsgleichung der Asymptote mittels einer
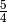 bei
bei 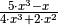 . Ist der Grad des Zählers kleiner als der Grad des
Nenners, so hat die gebrochenrationale Funktion für
. Ist der Grad des Zählers kleiner als der Grad des
Nenners, so hat die gebrochenrationale Funktion für 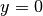 .
.