Lösungen zu Elektrizität und Magnetismus¶
Elektrische Ladung¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Elektrische Ladung.
Ladungen können nicht erzeugt oder vernichtet, sondern nur voneinander getrennt werden. Wenn zwei Körper aus unterschiedlichem Material aneinander gerieben werden, gibt der eine Körper negative Ladung (Elektronen) an den anderen ab.
Stromstärke, Spannung und Widerstand¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Stromstärke, Spannung und Widerstand.
Ohmsches Gesetz
Die Stromquelle stellt eine Spannung von
![U = \unit[5]{V}](../_images/math/c484c6523133fb58fa21d09175b4653e93ae8ff6.png) bereit, die
resultierende Stromstärke
bereit, die
resultierende Stromstärke ![I = \unit[0,2]{A}](../_images/math/bfa62be14617a0ff94b0ecfaaf13eb2e1ee1e522.png) . Aus dem Ohmschen Gesetz
ergibt sich für den Widerstand
. Aus dem Ohmschen Gesetz
ergibt sich für den Widerstand 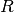 des Stromkreises:
des Stromkreises: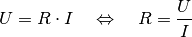
![R = \frac{\unit[5]{V}}{\unit[0,2]{A}} = \unit[25]{\Omega }](../_images/math/de295bc6482b4e6e20e57599b504f9140436b732.png)
Der Widerstand des Stromkreises beträgt somit
![R = \unit[25]{\Omega }](../_images/math/bfd97ca9536c8567921424f95acd9400c7109c28.png) .
.
Die Stromquelle stellt eine Spannung von
![U = \unit[12]{V}](../_images/math/57e2effb7546ef4df755ba9a8cb958435dd5958e.png) bereit, der
Widerstand des Stromkreises
bereit, der
Widerstand des Stromkreises ![R = \unit[800]{\Omega }](../_images/math/eb3f98ab6317faee3242590c221b70296d7c398c.png) . Aus dem Ohmschen
Gesetz ergibt sich für die Stromstärke
. Aus dem Ohmschen
Gesetz ergibt sich für die Stromstärke  im Stromkreis:
im Stromkreis: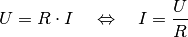
![I = \frac{\unit[12]{V}}{\unit[800]{\Omega }} = \unit[0,015]{A} =
\unit[15]{mA}](../_images/math/12ac09bc39af674f877e76952b9bf31164239095.png)
Die Stromstärke im Stromkreis beträgt somit
![I = \unit[15]{mA}](../_images/math/ab75914368645cbf9d0475d49a92e55bc9beb5ba.png) .
.
Die Stromquelle stellt eine Spannung von
![U = \unit[230]{V}](../_images/math/e76198dab697bebe6336196921c508d2eb227be3.png) bereit, der
Widerstand des Stromkreises
bereit, der
Widerstand des Stromkreises ![R = \unit[75]{\Omega }](../_images/math/ca1d7fe6b2921dd40cc27358d08f23f3da309282.png) . Aus dem Ohmschen
Gesetz ergibt sich für die Stromstärke
. Aus dem Ohmschen
Gesetz ergibt sich für die Stromstärke  im Stromkreis:
im Stromkreis: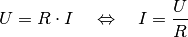
![I = \frac{\unit[230]{V}}{\unit[75]{\Omega }} \approx \unit[3,1]{A}](../_images/math/c797f8bc3618285f7011ce95873414d430e0c977.png)
Die Stromstärke im Stromkreis beträgt somit rund
![\unit[3,1]{A}](../_images/math/4bc767b3c03f4ceae92672dfd3056a534f2a1786.png) .
.
Der Widerstand im Stromkreis beträgt
![U = \unit[50]{\Omega}](../_images/math/128691b01ef8ed48e125d0b2c71ef85861e5ad48.png) , die
fließende Stromstärke
, die
fließende Stromstärke ![I = \unit[0,3]{A}](../_images/math/3c863b72431e8eb6d68029d770f2bb42913c9ed8.png) . Mit dem Ohmschen Gesetz
ergibt sich für die Spannung
. Mit dem Ohmschen Gesetz
ergibt sich für die Spannung  der Stromquelle:
der Stromquelle:![U = R \cdot I = \unit[50]{\Omega } \cdot \unit[0,3]{A} = \unit[15]{V}](../_images/math/97521c276565adbef9c2976bb6bc615ab6f0b123.png)
Die von der der Stromquelle bereitgestellte Spannung beträgt somit
![U =
\unit[15]{V}](../_images/math/e203cc496d08cbb103bdfd18440eff7351d3aecd.png) .
.
Die Stromquelle stellt eine Spannung von
![U = \unit[5]{V}](../_images/math/c484c6523133fb58fa21d09175b4653e93ae8ff6.png) bereit, die
resultierende Stromstärke
bereit, die
resultierende Stromstärke ![I = \unit[0,2]{A}](../_images/math/bfa62be14617a0ff94b0ecfaaf13eb2e1ee1e522.png) . Aus dem Ohmschen Gesetz
ergibt sich für den Widerstand
. Aus dem Ohmschen Gesetz
ergibt sich für den Widerstand 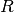 des Stromkreises:
des Stromkreises: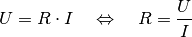
![R = \frac{\unit[230]{V}}{\unit[4]{A}} = \unit[5,75]{\Omega }](../_images/math/3b689eb5a415cb31e659c6888944bdc8c3dfb550.png)
Der Widerstand des Stromkreises beträgt somit
![R = \unit[5,75]{\Omega }](../_images/math/bfc613a3598aa2e7d3ec253b07fe61892b31051f.png) .
.
Spezifischer Widerstand
Der elektrische Widerstand
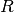 des Kupferdrahtes lässt sich anhand der
Formel
des Kupferdrahtes lässt sich anhand der
Formel 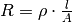 berechnen, indem man als Werte für
die Länge
berechnen, indem man als Werte für
die Länge ![l=\unit[10]{m}](../_images/math/7595196fdd2cbd3f6e6a557c57f551632b07c47e.png) , für den Querschnitt
, für den Querschnitt ![A = \pi \cdot
r^2 = \pi \cdot (\unit[2]{mm})^2 \approx \unit[12,6]{mm^2}](../_images/math/271e6fc38d1351f078fa097ddeadb763ca4bf296.png) und
und ![\rho
_{\mathrm{Cu}} = \unit[0,0156]{\Omega \cdot \frac{mm^2}{m} }](../_images/math/2e9a10cdfc3d0e3242a2ccef1e827943965f24e6.png) einsetzt:
einsetzt:![R = \rho \cdot \frac{l}{A} = \unit[0,0156]{\frac{\Omega \cdot mm^2}{m}
} \cdot \frac{\unit[10]{m}}{\unit[12,56]{mm^2}}
\approx \unit[0,12]{\Omega }](../_images/math/3940fe6382eb364929bf7187989f04488b3c4df6.png)
Der Draht hat einen elektrischen Widerstand von rund
![\unit[0,12]{\Omega }](../_images/math/5198a96424c7249dbbadc9569f4c3b3378138cc1.png) .
.
Der elektrische Widerstand
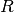 des Kupferdrahtes lässt sich mit Hilfe
der Formel
des Kupferdrahtes lässt sich mit Hilfe
der Formel 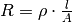 berechnen, indem man als Werte
für die Länge
berechnen, indem man als Werte
für die Länge ![l=\unit[11,4]{km} = \unit[11400]{m}](../_images/math/02b68927641ac1b5c023352e209b16142af814d7.png) , für den
Querschnitt
, für den
Querschnitt ![A = \pi \cdot r^2 = \pi \cdot (\unit[8,0]{mm})^2 \approx
\unit[201]{mm^2}](../_images/math/86ecaa4e71c30dc1c364b913d001830831e169a2.png) und
und ![\rho_{\mathrm{Cu}} = \unit[0,0156]{\Omega \cdot
\frac{mm^2}{m} }](../_images/math/fe14d658a1462a3e124f71f7b40edc74118f1464.png) einsetzt:
einsetzt:![R = \rho \cdot \frac{l}{A} = \unit[0,0156]{\frac{\Omega \cdot mm^2}{m}
} \cdot \frac{\unit[11400]{m}}{\unit[201]{mm^2}}
\approx \unit[0,89]{\Omega }](../_images/math/4be7b199d6ef1cb39c7cd75d91390979acd04969.png)
Für einen Draht aus Aluminium folgt in gleicher Weise:
![R = \rho \cdot \frac{l}{A} = \unit[0,0265]{\frac{\Omega \cdot mm^2}{m}
} \cdot \frac{\unit[11400]{m}}{\unit[201]{mm^2}}
\approx \unit[1,50]{\Omega }](../_images/math/97ffdf516fb0e6c8793b127f6bbe3abde449fcb3.png)
Für einen Draht aus Edelstahl ergibt sich:
![R = \rho \cdot \frac{l}{A} = \unit[0,720]{\frac{\Omega \cdot mm^2}{m}
} \cdot \frac{\unit[11400]{m}}{\unit[201]{mm^2}}
\approx \unit[40,8]{\Omega }](../_images/math/0efa2171a2a0f43c9085f2e3e9499651d20a8d6e.png)
Der Kupferdraht hat einen elektrischen Widerstand von rund
![\unit[0,89]{\Omega }](../_images/math/41d798f06b3e3089a06c47c0dba41a96c297691c.png) . Baugleiche Drähte aus Aluminium bzw. Eisen
hätten elektrische Widerstände von
. Baugleiche Drähte aus Aluminium bzw. Eisen
hätten elektrische Widerstände von ![\unit[1,50]{\Omega }](../_images/math/287982e3a91a892d7dba6eae9380d97e698a25be.png) bzw.
bzw.
![\unit[40,8]{\Omega }](../_images/math/9ce03059da406cb67a101d059b7fcb96fbfb6c5f.png) .
.
Den nötigen Radius des Eisendrahts erhält man, indem man die Formel
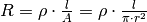 nach
nach
 auflöst:
auflöst:
Setzt man hierbei den spezifischen Widerstand von Eisen
![\rho_{\mathrm{Fe}} = \unit[0,125]{\Omega \cdot \frac{mm^2}{m} }](../_images/math/0a4d97abfea5e03e879327fa6c97f9848498f1e4.png) , für
die Länge
, für
die Länge ![l = \unit[50]{m}](../_images/math/41fd94528d5bd9532267b3a36c983f0de274cd7e.png) und für den maximalen Widerstand
und für den maximalen Widerstand ![R =
\unit[1]{\Omega }](../_images/math/5d2cb1c4c4b85cbb62debe90a61630b66e91cef0.png) ein, so erhält man:
ein, so erhält man:![r = \sqrt{\rho \cdot \frac{l}{\pi \cdot R} } = \sqrt{ \unit[0,125]{\Omega
\cdot \frac{mm^2}{m} } \cdot \frac{\unit[10]{m}}{\pi \cdot
\unit[1]{\Omega }} } \approx \unit[1,41]{mm}](../_images/math/72974ab7ea0c301c9e4aab4119cdac1dac50afc0.png)
Der Draht muss somit einen Durchmesser von mindestens
![2 \cdot r
\approx \unit[2,82]{mm}](../_images/math/9540d2330292550b413f85d14ef2336a049eaaa3.png) haben.
haben.
Elektrische Felder¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Elektrische Felder.
Für die im Kondensator gespeicherte Energie gilt:
![E = \frac{1}{2} \cdot C \cdot U^2 = \frac{1}{2} \cdot \unit[220 \cdot
10^{-6}]{F} \cdot \left( \unit[6,0]{V} \right)^2 = \unit[0,00396]{J}](../_images/math/1d892f80f03d60e3abde68d88f93f4682af3c540.png)
Die Einheit ergibt sich aus folgender Beziehung:
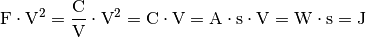
Die beim Entladen des Kondensators freigesetzte Energie beträgt somit knapp
![\unit[4]{mJ}](../_images/math/9dc717bcf486d1c7c1ccc8863949742712330193.png) . Die Energiemenge ist zwar nicht groß, sie wird
allerdings in einer sehr kurzen Zeit umgesetzt. Nimmt man
. Die Energiemenge ist zwar nicht groß, sie wird
allerdings in einer sehr kurzen Zeit umgesetzt. Nimmt man ![\Delta t =
\unit[0,1]{s}](../_images/math/124436d616e11458f0b16ff022be0de718134291.png) an, so erhält man für die beim Blitzvorgang zur Verfügung
gestellte Leistung etwa
an, so erhält man für die beim Blitzvorgang zur Verfügung
gestellte Leistung etwa ![P = \tfrac{\Delta E}{\Delta t} \approx
\unit[39,6]{W}](../_images/math/c599a202b9936e38a21f6c10bd7671a849bbb9b7.png) .
.
Für den Zusammenhang zwischen der Kapazität
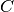 , der Ladung
, der Ladung 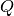 und der Spannung
und der Spannung  gilt für einen Plattenkondensator:
gilt für einen Plattenkondensator:
Setzt man zudem
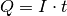 ein, so erhält man bei einer konstanten
Stromstärke
ein, so erhält man bei einer konstanten
Stromstärke  für
für ![t=\unit[1]{s},\,\unit[2]{s},\,\ldots](../_images/math/015232e5c5aa841f8fc551334c980dbb4a38de7f.png) :
:![U(\unit[1]{s}) &= \frac{\unit[0,003]{A} \cdot \unit[1]{s}}{\unit[470 \cdot
10^{-6}]{F}} \approx \unit[\phantom{1}6,38]{V} \\
U(\unit[2]{s}) &= \frac{\unit[0,003]{A} \cdot \unit[2]{s}}{\unit[470 \cdot
10^{-6}]{F}} \approx \unit[12,76]{V} \\
U(\unit[3]{s}) &= \frac{\unit[0,003]{A} \cdot \unit[3]{s}}{\unit[470 \cdot
10^{-6}]{F}} \approx \unit[19,15]{V} \\
U(\unit[3]{s}) &= \frac{\unit[0,003]{A} \cdot \unit[4]{s}}{\unit[470 \cdot
10^{-6}]{F}} \approx \unit[25,53]{V} \\
U(\unit[3]{s}) &= \frac{\unit[0,003]{A} \cdot \unit[5]{s}}{\unit[470 \cdot
10^{-6}]{F}} \approx \unit[31,91]{V} \\](../_images/math/56f75ef5c7f5cfbdda9c01d554846b5c4cbd7790.png)
Die Einheit ergibt sich aus folgender Beziehung:
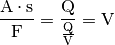
Die gespeicherten Energiemengen können mittels dieser Ergebnisse anhand der Formel
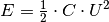 berechnet werden:
berechnet werden:![E(\unit[1]{s)} &= \frac{1}{2} \cdot \unit[470 \cdot 10^{-6}]{F} \cdot
\left( \unit[\phantom{1}6,38]{V} \right)^2 \approx \unit[0,0096]{J} \\
E(\unit[2]{s)} &= \frac{1}{2} \cdot \unit[470 \cdot 10^{-6}]{F} \cdot
\left( \unit[12,76]{V} \right)^2 \approx \unit[0,0383]{J} \\
E(\unit[3]{s)} &= \frac{1}{2} \cdot \unit[470 \cdot 10^{-6}]{F} \cdot
\left( \unit[19,15]{V} \right)^2 \approx \unit[0,0862]{J} \\
E(\unit[4]{s)} &= \frac{1}{2} \cdot \unit[470 \cdot 10^{-6}]{F} \cdot
\left( \unit[25,53]{V} \right)^2 \approx \unit[0,1532]{J} \\
E(\unit[5]{s)} &= \frac{1}{2} \cdot \unit[470 \cdot 10^{-6}]{F} \cdot
\left( \unit[31,91]{V} \right)^2 \approx \unit[0,2394]{J} \\](../_images/math/c8bd73f225b77719f05e55ff84ec6198756160da.png)
Die Einheit ergibt sich aus folgender Beziehung:
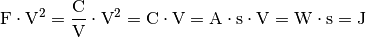
Üblicherweise ist jedoch – anders als bei dieser Aufgabe – die Stromstärke beim Laden eines Kondensators nicht konstant (siehe Ladekurve eines Kondensators).
Lösungen zu Magnetismus¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Magnetismus.
Wenn der Nordpol der Magnetnadel – geographisch gesehen – nach Norden zeigt, so muss sich dort der magnetische Südpol der Erde befinden; der magnetische Nordpol der Erde befindet sich entsprechend (näherungsweise) am geographischen Südpol.
Elektrische Arbeit, Energie und Leistung¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Elektrische Arbeit, Energie und Leistung.
Mit Hilfe der Definition der elektrischen Leistung
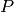 kann die
fließende Stromstärke
kann die
fließende Stromstärke  folgendermaßen ausgedrückt werden:
folgendermaßen ausgedrückt werden: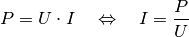
Durch Einsetzen der Werte erhält man für eine
![P = \unit[40]{W}](../_images/math/0ffee43e3c42b6485cbddaedbf9094bada587d96.png) -Glühbirne, die mit
-Glühbirne, die mit ![U = \unit[230]{V}](../_images/math/e76198dab697bebe6336196921c508d2eb227be3.png) betrieben wird:
betrieben wird:![I = \frac{P}{U} = \frac{\unit[40]{W}}{\unit[230]{V}} \approx
\unit[0,17]{A}](../_images/math/52f3fdac30a1d78fead7f5cfe4b87c7b9bca0b2b.png)
Die Stromstärke in der Glühbirne beträgt somit rund
![\unit[0,17]{A}](../_images/math/adba33bf7b857fcffd928cee421c72a9cd445ac5.png) .
Wird die Glühbirne
.
Wird die Glühbirne ![t=\unit[6]{h}](../_images/math/bd5529993237a048484608770f063660b7637e75.png) lang betrieben, so wird folgende
Menge an elektrischer Energie in Licht und Wärme umgewandelt:
lang betrieben, so wird folgende
Menge an elektrischer Energie in Licht und Wärme umgewandelt:![E = P \cdot t = \unit[40]{W} \cdot \unit[6]{h} = \unit[240]{W \cdot h} =
\unit[0,24]{kWh}](../_images/math/c0e228eefaa8b1a89e73581d5957f9a585641f7e.png)
Es werden somit
![\unit[0,24]{kWh}](../_images/math/3c1e5ac1fda06925b5c3e0852c291b92b5deea15.png) an elektrischer Energie benötigt.
an elektrischer Energie benötigt.Die Ladungsmenge
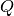 , die innerhalb der angegebenen Zeit durch die
Glühbirne fließt, kann folgendermaßen berechnet werden:
, die innerhalb der angegebenen Zeit durch die
Glühbirne fließt, kann folgendermaßen berechnet werden:![I = \frac{\Delta Q}{\Delta t} \quad \Longleftrightarrow \quad \Delta Q = I
\cdot \Delta t = \unit[0,17]{A} \cdot \unit[6 \cdot 3600]{s} =
\unit[3672]{C}](../_images/math/ed75b44e3a069def3d1b871cca8a16f670593854.png)
Es fließen somit innerhalb von sechs Stunden knapp
![\unit[3,7 \cdot
10^{3}]{C}](../_images/math/1b02f90ca95a7b3b23416b98f4cde5af49d3abc4.png) an elektrischer Ladung durch die Glühbirne.
an elektrischer Ladung durch die Glühbirne.
Aus der angegebenen Leistung
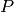 und der Spannung
und der Spannung  kann man
zunächst die Stromstärke
kann man
zunächst die Stromstärke  berechnen:
berechnen:![P = U \cdot I \quad \Longleftrightarrow \quad I = \frac{P}{U} =
\frac{\unit[2,5]{W}}{\unit[6,0]{V}} \approx \unit[0,417]{A}](../_images/math/f1a5c885f26165bc37f4d90ea9ff4c5b33573fdc.png)
Für die Stromstärke gilt zudem die Beziehung
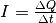 ; für die Ladungsmenge
; für die Ladungsmenge 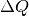 , die in der Zeitspanne
, die in der Zeitspanne
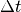 durch die Glühbirne fließt, gilt somit:
durch die Glühbirne fließt, gilt somit:![\Delta Q = I \cdot \Delta t = \unit[0,417]{A} \cdot \unit[(5 \cdot 60)]{s}
= \unit[125]{C}](../_images/math/1cdb5626192a41d7d87a60d71481f25309bf44b0.png)
Diese Ladungsmenge entspricht folgender Anzahl
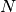 an Elektronen:
an Elektronen:![Q = N \cdot e \quad \Longleftrightarrow \quad N = \frac{Q}{e} =
\frac{\unit[125]{C}}{\unit[1,6 \cdot 10^{-19}]{C}} \approx 7,8 \cdot
10^{20}](../_images/math/0102d442711b3a0da5a1ab4f00a41f15d23f3cdb.png)
Es fließen in den fünf Minuten somit rund
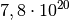 Elektronen
durch die Glühbirne.
Elektronen
durch die Glühbirne.
Mit Hilfe der Definition der elektrischen Leistung
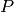 lässt sich die
fließende Stromstärke
lässt sich die
fließende Stromstärke  folgendermaßen ausdrücken:
folgendermaßen ausdrücken: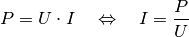
Durch Einsetzen der Werte erhält man für einen
![P =
\unit[1\,800]{W}](../_images/math/dd80316789e7d4699b4c66c9bdca02273e25d305.png) -Wasserkocher, der mit
-Wasserkocher, der mit ![U = \unit[230]{V}](../_images/math/e76198dab697bebe6336196921c508d2eb227be3.png) betrieben
wird:
betrieben
wird:![I = \frac{P}{U} = \frac{\unit[1\,800]{W}}{\unit[230]{V}} \approx
\unit[7,83]{A}](../_images/math/68e59beb09780466ae69b0211f13a829569d5619.png)
Die Stromstärke im Wasserkocher beträgt somit rund
![\unit[7,83]{A}](../_images/math/e55212a6e75de8de4564a74ed4afd15c553e6e94.png) .
.
Für die elektrische Leistung gilt
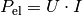 . Für die
Stromstärke
. Für die
Stromstärke  kann wiederum aufgrund des Ohmschen Gesetzes
kann wiederum aufgrund des Ohmschen Gesetzes 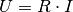 auch
auch 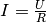 geschrieben werden. Damit ergibt sich:
geschrieben werden. Damit ergibt sich: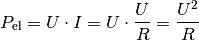
Ist
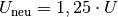 , so folgt für das Verhältnis aus
, so folgt für das Verhältnis aus
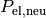 zu
zu 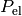 :
: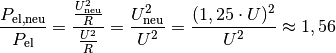
Die elektrische Leistung nimmt somit um rund
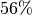 zu.
zu.
