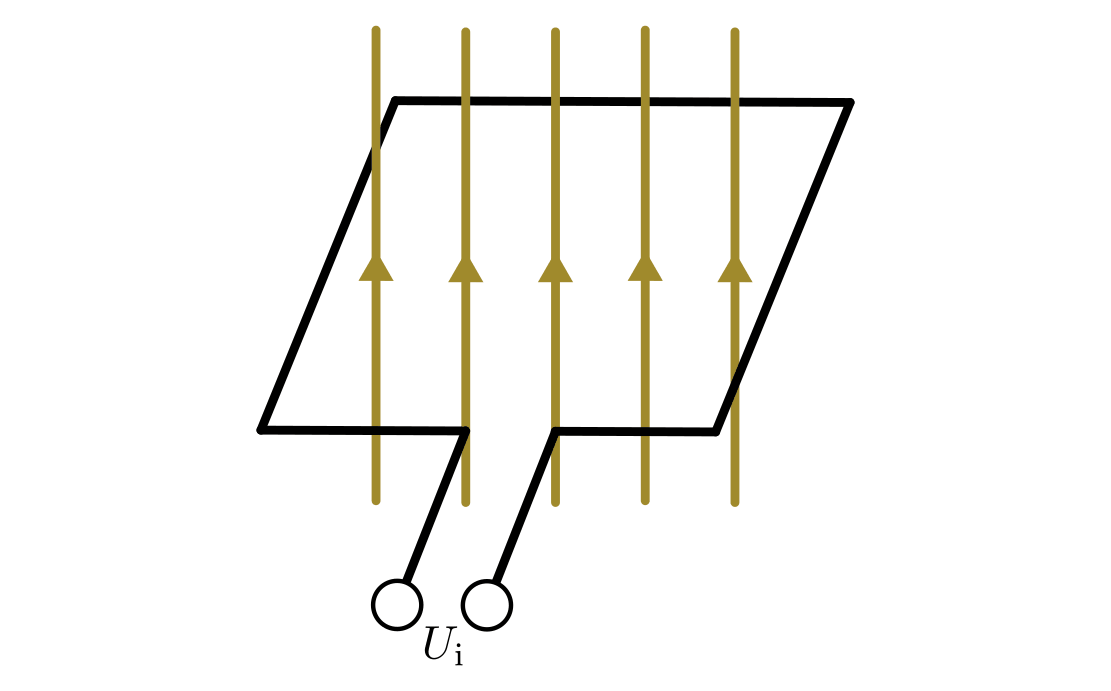Magnetismus¶
Bereits seit der Antike kennen und nutzen die Menschen magnetische Erscheinungen. Insbesondere die Verwendung von dünnen, drehbar gelagerten Magnetscheiben in Kompassen war in vielerlei Hinsicht „richtungsweisend“ für die Entwicklung der Menschheit. Inzwischen sind insbesondere Elektromagnete, Elektromotoren, Generatoren und Transformatoren aus unserer modernen Gesellschaft nicht mehr wegzudenken.
Permanentmagnete¶
Wohl am bekanntesten ist die anziehende Wirkung von Magneten auf Eisen. Stoffe, die ebenso wie Eisen von Magneten angezogen werden und dabei selbst magnetisiert werden, bezeichnet man nach dem lateinischen Namen von Eisen („ferrum“) als „ferromagnetisch“ oder umgangssprachlich kurz als „magnetisch“. Hierzu zählen Kobalt, Nickel, Neodym, und wenige Legierungen.
Auf nicht-ferromagnetische Stoffe zeigen Magnete (fast) keine Wirkung.
Das Modell der Elementarmagnete
Magnete besitzen stets zwei gegenüberliegende Bereiche, an denen ihre magnetische Wirkung besonders stark ist. Diese Bereiche werden als Magnetpole bezeichnet.
Zerbricht ein Magnet in zwei Teile, so stellt man fest, dass beide Teilstücke ihrerseits zwei Magnetpole besitzen. Auch bei weiterer Teilung treten die Magnetpole stets paarweise auf. Umgekehrt kann jeder Magnet aus einer Vielzahl kleinster „Elementarmagnete“ aufgefasst werden:
- Zeigen alle Elementarmagnete eines Magneten geordnet in die gleiche Richtung, so verstärken sie sich in ihrer Wirkung – ein starkes Magnetfeld ist die Folge.
- Zeigen die Elementarmagnete in unterschiedliche Richtungen, so heben sich ihre Wirkungen gegenseitig auf.
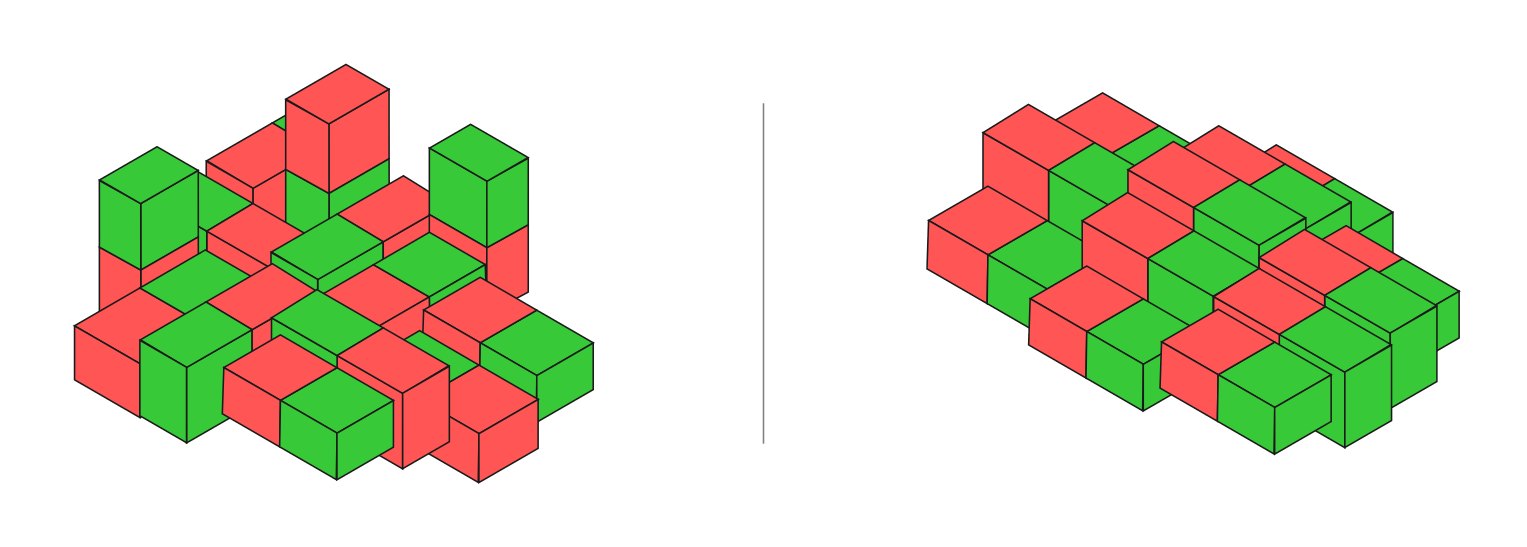
Die Elementarmagnete eines magnetisierbaren Materials besitzen unterschiedliche Ausrichtungen. In einem magnetisierten Material weisen die Elementarmagnete hingegen eine einheitliche magnetische Ordnung auf.
Anders als bei elektrischen Ladungen existieren bei Magneten keine „Mono-Pole“, sondern nur „Di-Pole“: Bei einem Magneten treten Nord- und Südpol niemals einzeln, sondern stets in Kombination miteinander auf.
Magnetische Influenz
In nicht magnetisiertem Eisen sind die Elementarmagnete bereichsweise geordnet. Diese so genannten „Weißsche Bezirke“ besitzen ihrerseits allerdings unterschiedliche Ausrichtungen, so dass ein Stück Eisen von sich aus keine magnetische Wirkung auf andere Körper ausübt.
Eisen kann durch Annähern eines Magneten selbst zum Magneten werden. Bei diesem Vorgang, den man als „magnetische Influenz“ bezeichnet, folgen die einzelnen Elementarmagnete wie Kompassnadeln dem äußeren Magnetfeld. Da sich die Wirkungen der einzelnen Elementarmagnete addieren, wirkt das Eisen dadurch auch nach außen hin als Magnet.
In welchem Maß die magnetische Ordnung erhalten bleibt, wenn der äußere Magnet wieder entfernt wird, hängt von der Zusammensetzung des magnetisierten Stoffes ab:
- Bei magnetisch „weichen“ Materialien, beispielsweise Weicheisen, verschwindet der durch Influenz hervorgerufene Magnetismus (weitgehend) wieder.
- In magnetisch „harten“ Materialien, beispielsweise Stahl, bleibt die magnetische Wirkung dauerhaft erhalten.
Erschütterungen oder starkes Erhitzen können die Ordnung der Elementarmagnete
wieder zerstören. Für alle Stoffe lässt sich eine bestimmte Temperatur
(„Curie-Temperatur“) angeben, oberhalb derer die thermische Bewegung der
Stoffteilchen eine magnetische Ordnung verhindert. Beispielsweise ist Eisen ab
![\unit[770]{\degree C}](../_images/math/5d0194a1262a1224739d601c9453350687dcc413.png) nicht mehr magnetisierbar.
nicht mehr magnetisierbar.
Das Magnetfeld¶
Die Kraft, die ein Magnet auf einen anderen magnetischen Körper ausübt, ist abhängig vom Abstand der Magnete, ihrer Form und von ihrer Ausrichtung zueinander.
Die stärkste Kraft zeigt ein Magnet an seinen beiden gegenüberliegenden Polen:
- Magnetisierbare Körper (beispielsweise Büroklammern aus Eisen) werden von beiden Magnetpolen gleichermaßen stark angezogen (Magnetische Influenz).
- Permanent- und Elektromagnete erfahren bei Annäherung ihrer Magnetpole je nach Ausrichtung eine starke anziehende oder abstoßende Wirkung. Werden die Magnetpole – in Anlehnung an das Erdmagnetfeld – als Nord- bzw. Südpol bezeichnet, so zeigt sich, dass sich Nord- und Südpole gegenseitig anziehen, während sich Nord- und Nordpole bzw. Süd- und Südpole gegenseitig abstoßen.
Die magnetische Kraft ist in unmittelbarer Nähe zu den Magnetpolen am stärksten und nimmt mit zunehmendem Abstand von den Magnetpolen ab.
Die Abhängigkeit der Magnetkräfte von der Form des Magneten lässt sich am leichtesten mit Hilfe von Eisenfeilspänen beobachten. Diese werden an unterschiedlichen Stellen um den Magneten herum verschieden stark ausgelenkt bzw. angezogen, so dass sich jeweils ein für die Form des Magneten charakteristisches Muster ergibt.
Auch eine Magnetnadel lenkt sich, wenn sie um einen Magneten herum bewegt wird, an jeder Stelle in der gleicher Richtung wie die Eisenfeilspäne aus, wobei sich der Nordpol der Magnetnadel stets zum Südpol des Magneten hin orientiert.
Die geschlossenen Linien, die sich in den Mustern der Eisenfeilspäne um den Magneten herum ergeben, deuten somit jeweils auf die Richtung der Magnetkraft hin. Man bezeichnet diese räumliche Verteilung der Magnetkräfte um den Magneten herum als „Magnetfeld“ und stellt sie in technischen Zeichnungen (etwas vereinfacht) durch einige stets geschlossene Linien dar. Oftmals werden noch entlang dieser „Magnetfeldlinien“ kleine Pfeile eingezeichnet, die jeweils am Nordpol aus dem Magneten aus- und am Südpol wieder eintreten.
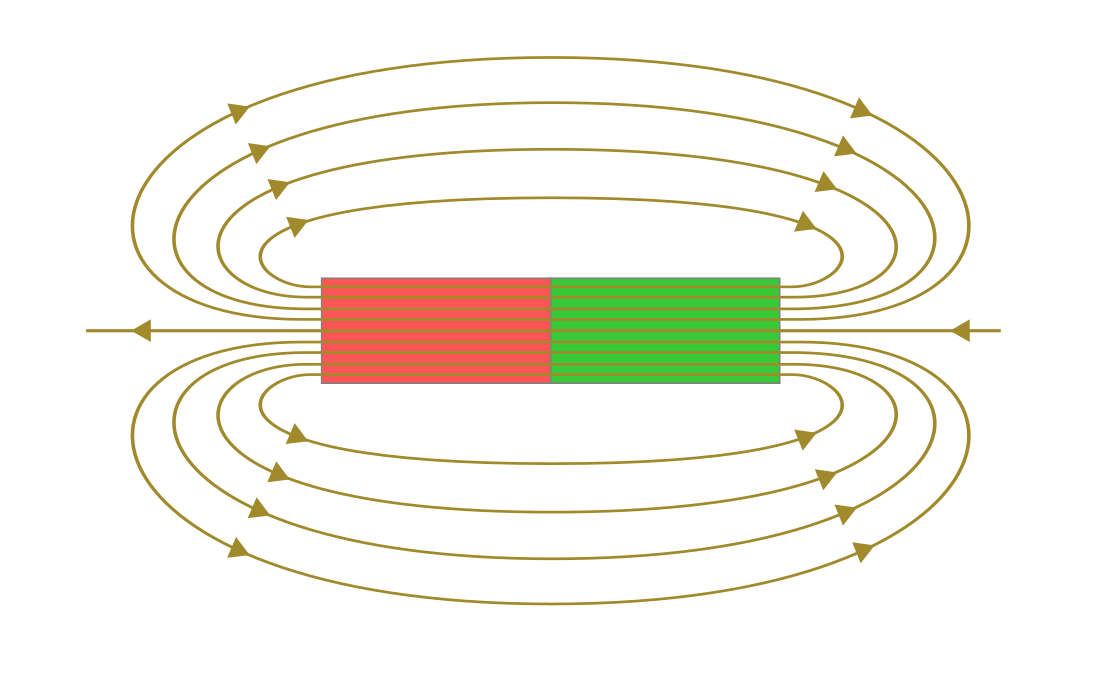
Die Magnetfeldlinien eines Stabmagneten treten am magnetischen Nordpol aus und am Südpol wieder ein.
Auf diese Weise kann sowohl die Kraftwirkung eines Magneten visualisiert werden als auch sein Einfluss auf andere magnetische bzw. magnetisierbare Körper abgeschätzt werden.
Zusammenfassung:
- Magnetpole treten stets paarweise auf. Entlang diesen verlaufen die Magnetfeldlinien auf stets geschlossenen Bahnen.
- Die Pfeile der Magnetfeldlinien zeigen innerhalb des Magneten in Richtung Nordpol, außerhalb des Magneten in Richtung Südpol.
- Gleiche Magnetpole stoßen sich ab, unterschiedliche Magnetpole ziehen sich an.
- Die magnetische Wirkung nimmt mit zunehmendem Abstand von den Magnetpolen ab.
- Sind mehrere Magneten in gleicher Richtung ausgerichtet, so verstärken sich ihre Wirkungen zu einem Gesamtmagnetfeld. Bei wechselnder Ausrichtung ist nach außen hin (fast) keine magnetische Wirkung feststellbar.
- Magnetfelder lassen sich bereits durch dünne magnetisierbare Platten (beispielsweise aus Eisen) abschirmen, durchdringen hingegen nicht magnetisierbare Materialien nahezu ohne Abschwächung.
Elektromagnete¶
Im Jahr 1820 entdeckte Hans-Christian Oersted, dass auch von einem stromdurchflossenen elektrischen Leiter eine (schwache) Kraftwirkung auf eine nahe gelegene Kompassnadel ausgeht. Diese Feststellung widersprach der bis dahin gängigen Auffassung, dass es sich bei Elektrizität und Magnetismus um zwei voneinander getrennte Phänomene handele.
Durch verschiedene Positionierungen des elektrischen Leiters und der Magnetnadel(n) konnte Örsted in gleicher Weise wie bei Permanentmagneten das schwache Magnetfeld des Leiters bestimmen. Er konnte folgende Gesetzmäßigkeit beobachten:
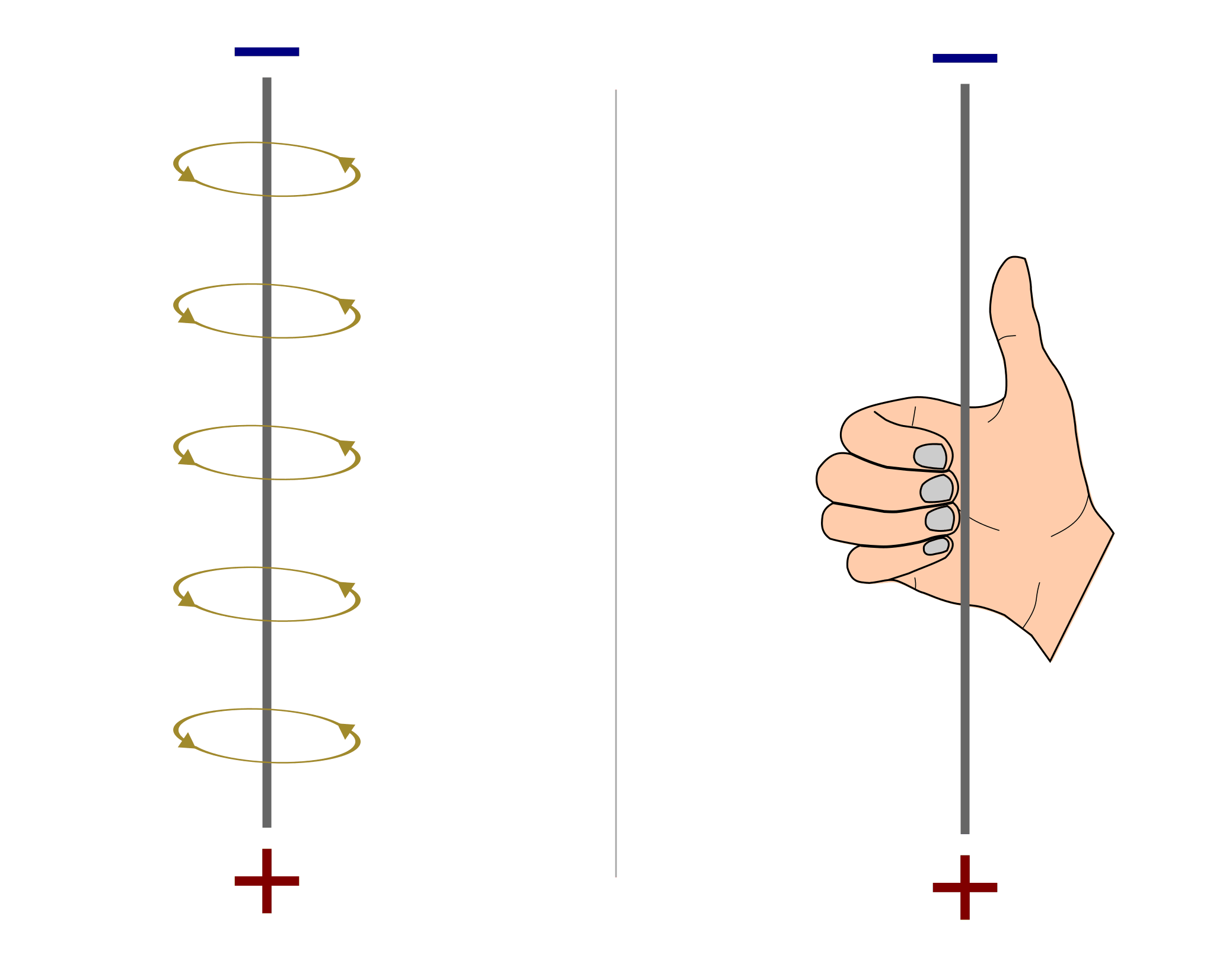
Rechte-Hand-Regel (für Leiterbahnen):
Umfasst man einen stromdurchflossenen geraden Leiter mit der rechten Hand so, dass der ausgestreckte Daumen entlang der technischen Stromrichtung (von+nach-) zeigt, dann geben die übrigen Finger die Richtung der magnetischen Feldlinien an.
Die Rechte-Hand-Regel gilt auch, wenn der elektrische Leiter zu einer Kreisform gebogen wird. Der Daumen muss hierbei mit der Krümmung des Leiters mitgeführt werden, um stets in die technische Stromrichtung zu zeigen. Es stellt sich dabei heraus, dass das resultierende Magnetfeld an den verschiedenen Stellen der Leiterschleife stets in die gleiche Richtung zeigt.
Beispiel:
- Liegt die Leiterschleife auf einem Tisch und verläuft die technische Stromrichtung entgegen des Uhrzeigersinns, so zeigt das Magnetfeld im Inneren der Leiterschleife an jeder Stelle senkrecht nach oben. (Auf der Außenseite der Leiterschleife zeigt es senkrecht nach unten.)
Die Kraftwirkungen an den einzelnen Stellen des elektrischen Leiters addieren sich bei einer Leiterschleife somit zu einem Gesamtmagnetfeld, das an die Form eines Ringmagneten erinnert. Dieser Effekt lässt sich noch wesentlich verstärken, indem mehrere Leiterschleifen übereinander gelegt werden bzw. ein langer Leiter zu einer Spule gewickelt wird.
Das Magnetfeld einer stromdurchflossenen Spule
Eine lange stromdurchflossene Spule mit vielen Windungen erzeugt nach außen hin ein Magnetfeld, das dem eines Stabmagneten sehr ähnlich ist. Hierbei gibt wieder die Rechte-Hand-Regel Auskunft, in welcher Richtung sich der Nord- bzw. Südpol des „Elektromagneten“ befindet.
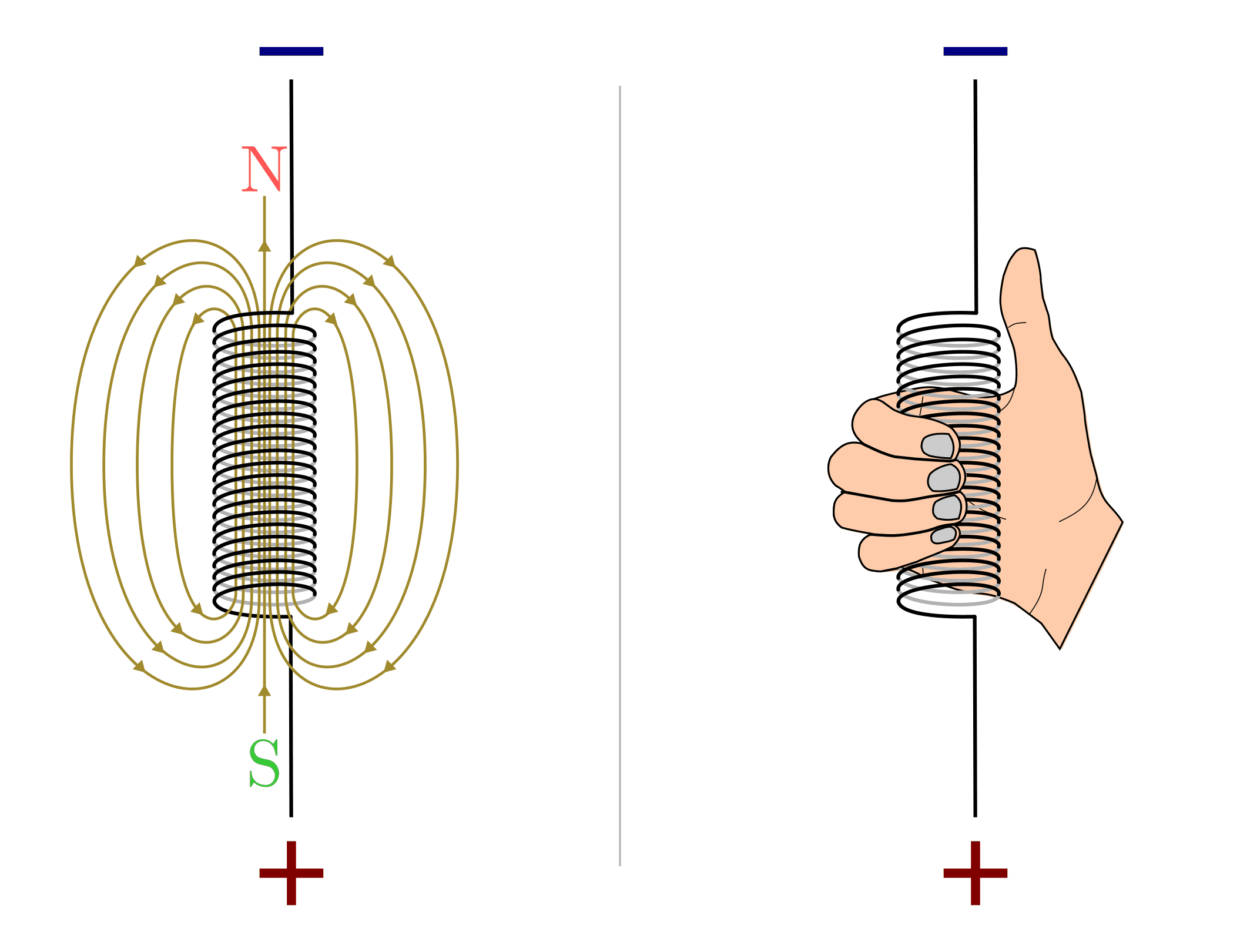
Rechte-Hand-Regel (für Spulen):
Umfasst man die Windungen einer Spule mit der rechten Hand so, dass die Finger in die technische Stromrichtung zeigen, dann liegt der magnetische Nordpol der Spule in Richtung des ausgestreckten Daumens.
Die magnetische Wirkung einer stromdurchflossenen Spule kann zusätzlich gesteigert werden, indem durch die Spule ein Stück nicht magnetisiertes Eisen gelegt wird. Durch die magnetische Influenz wird das Eisen selbst magnetisch und verstärkt die magnetische Wirkung der Spule erheblich.
Elektromagnete haben gegenüber Permanentmagneten folgende Vorteile:
- Elektromagnete lassen sich ein- und ausschalten.
- Die Stärke eines Elektromagneten lässt sich durch die Stromstärke in der Spule regulieren.
- Nord- und Südpol eines Elektromagneten lassen sich vertauschen, indem die Plus- und Minuspole der anliegenden Spannung getauscht werden.
- Elektromagnete sind fast nicht zerbrechlich, verlieren im Lauf der Zeit nicht an Stärke, und sind kostengünstig herzustellen.
Magnetische Feldstärke und magnetische Flussdichte¶
Quantitativ kann die Kraftwirkung eines Magnetfelds durch die so genannte
magnetische Feldstärke 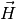 beschrieben werden.
beschrieben werden.
Bei einer geraden Leiterbahn ist die magnetische Feldstärke proportional zur
fließenden Stromstärke 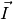 und umgekehrt proportional zum Abstand
und umgekehrt proportional zum Abstand
 von der Leiterbahn. Es gilt also:
von der Leiterbahn. Es gilt also:
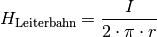
Die Einheit der magnetischen Feldstärke ist gemäß der obigen Formel
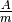 .
.
Im Inneren einer Leiterschleife ist der Wert der magnetischen Feldstärke
gegenüber einer geraden Leiterbahn um den Faktor 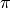 erhöht, es gilt
also
erhöht, es gilt
also 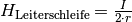 . Kombiniert man
eine Zahl
. Kombiniert man
eine Zahl 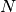 an Leiterschleifen zu einer langen Spule, so ist die
magnetische Feldstärke im Inneren der Spule nahezu „homogen“, die Feldlinien
verlaufen also parallel zueinander. Für die magnetische Feldstärke einer Spule
mit einer Windungszahl
an Leiterschleifen zu einer langen Spule, so ist die
magnetische Feldstärke im Inneren der Spule nahezu „homogen“, die Feldlinien
verlaufen also parallel zueinander. Für die magnetische Feldstärke einer Spule
mit einer Windungszahl 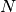 und einer Länge
und einer Länge  gilt:
gilt:
(1)¶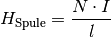
Eine zweite wichtige Größe zur Beschreibung von magnetischen Feldern ist die so
genannte magnetische Flussdichte 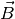 . Sie gibt anschaulich an, wie
viele Feldlinien durch eine bestimmte Fläche hindurchgehen. Zwischen der
magnetischen Flussdichte, welche die räumliche Verteilung der Feldlinien
kennzeichnet, und die magnetische Feldstärke, welche die Kraftwirkung auf andere
Magneten beschreibt, gibt es folgenden Zusammenhang:
. Sie gibt anschaulich an, wie
viele Feldlinien durch eine bestimmte Fläche hindurchgehen. Zwischen der
magnetischen Flussdichte, welche die räumliche Verteilung der Feldlinien
kennzeichnet, und die magnetische Feldstärke, welche die Kraftwirkung auf andere
Magneten beschreibt, gibt es folgenden Zusammenhang:
(2)¶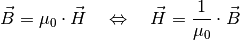
Hierbei bezeichnet ![\mu_0 = \unit[1,256 \cdot 10 ^{-6}]{\frac{V \cdot
s}{A \cdot m}}](../_images/math/aa5ebeca0c65648fddf99a693587e45b29b52e7b.png) die magnetische Feldkonstante. Für die magnetische Flussdichte
ergibt sich damit als Einheit:
die magnetische Feldkonstante. Für die magnetische Flussdichte
ergibt sich damit als Einheit:
![[B] = \unit[1]{\frac{V \cdot s}{m^2}} = \unit[1]{Tesla} = \unit[1]{T}](../_images/math/b4884b41edbef40e81bf510c46bcbc39830e7630.png)
Beispielsweise beträgt die magnetische Flussdichte der Erde rund
![\unit[0,04]{mT}](../_images/math/bf40d7e690243de1ba861d02883c7755684c96fd.png) .
.
Der obige Zusammenhang (2) gilt streng genommen nur im Vakuum, in guter Näherung jedoch auch in Luft. Befindet sich jedoch ein anderes Material im Magnetfeld, so muss dessen so genannte Permeabilität berücksichtigt werden, die angibt, ob die durch das Material laufenden Feldlinien durch das Material eher zusammengezogen oder aus dem Material hinausgedrängt werden. Allgemein gilt also:
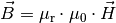
Für die Größe der Permeabilitätszahl 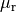 gibt es im
wesentlichen drei verschiedene Fälle:
gibt es im
wesentlichen drei verschiedene Fälle:
- In diamagnetischen Materialien
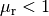 , die magnetische
Flussdichte wird also gegenüber dem äußeren Feld leicht verringert. Beispiele:
Kupfer, Zink, Wasser, Stickstoff.
, die magnetische
Flussdichte wird also gegenüber dem äußeren Feld leicht verringert. Beispiele:
Kupfer, Zink, Wasser, Stickstoff. - In paramagnetischen Materialien ist
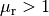 , die magnetische
Flussdichte wird also gegenüber dem äußeren Feld leicht erhöht. Beispiele:
Aluminium, Platin, Sauerstoff.
, die magnetische
Flussdichte wird also gegenüber dem äußeren Feld leicht erhöht. Beispiele:
Aluminium, Platin, Sauerstoff. - In ferromagnetischen Materialien ist
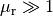 , ist die magnetische
Flussdichte wird also gegenüber dem äußeren Feld stark erhöht. Beispiele:
Eisen, Cobalt, Nickel.
, ist die magnetische
Flussdichte wird also gegenüber dem äußeren Feld stark erhöht. Beispiele:
Eisen, Cobalt, Nickel.
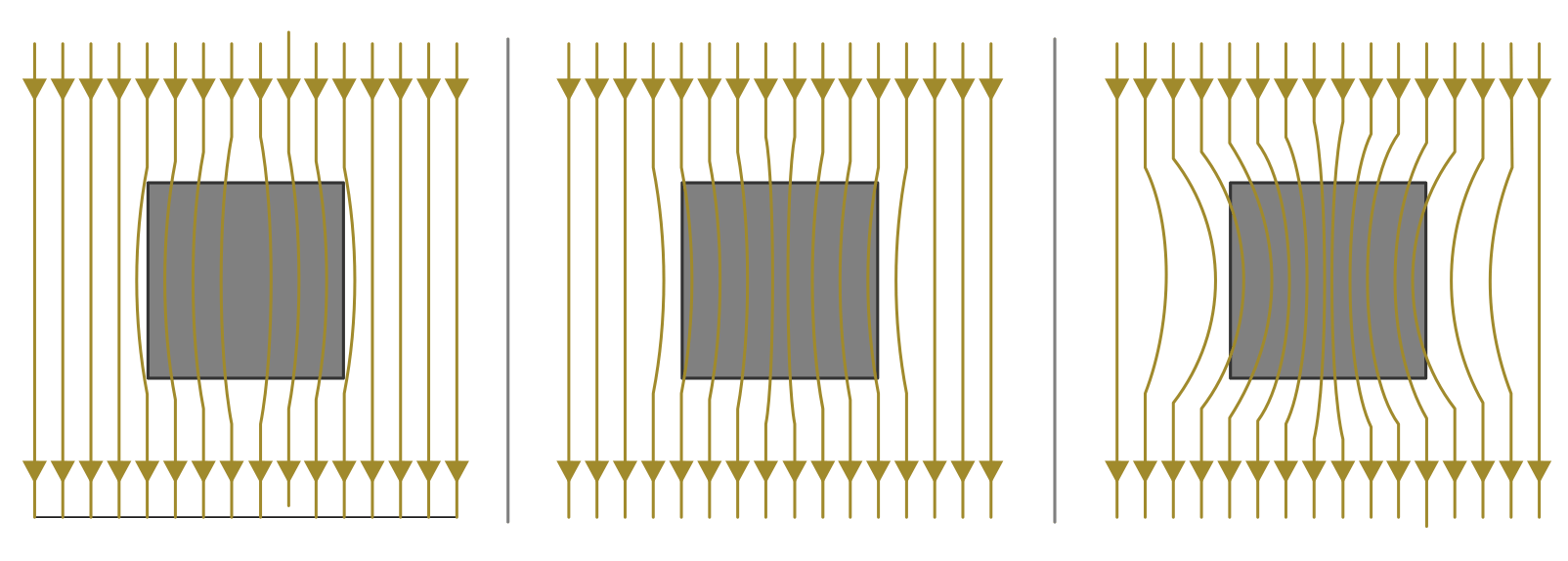
Feldlinienverlauf bei einer diamagnetischen, paramagnetischen und ferromagnetischen Material (von links nach rechts).
Die Permeabilitätszahlen von dia- und paramagnetischen Materialien sind meist
nur wenig von 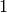 verschieden, so dass die magnetischen Eigenschaften
dieser Materialien in technischen Anwendungen nur selten eine Rolle spielen.
verschieden, so dass die magnetischen Eigenschaften
dieser Materialien in technischen Anwendungen nur selten eine Rolle spielen.
Die Lorentz-Kraft¶
Während jeder elektrische Stromfluss ein Magnetfeld zur Folge hat, so hat gleichermaßen jedes Magnetfeld einen Einfluss auf einen elektrischen Strom.
Befindet sich ein Stück eines stromdurchflossenen Leiters in einem Magnetfeld, so wirkt auf das Leiterstück eine Kraft. Sie wird nach ihrem Entdecker Hendrik Antoon Lorentz als „Lorentz-Kraft“ bezeichnet. Der Betrag der Kraft hängt von der Stärke Stromflusses bzw. Magnetfeldes sowie vom Winkel zwischen Leiter und Magnetfeld ab:
- Der Betrag der Kraft ist am größten, wenn der Leiter senkrecht zum Magnetfeld ausgerichtet ist.
- Zeigen der Leiter und das Magnetfeld in die gleiche Richtung, so wirkt keine Kraft.
Die Lorentz-Kraft wirkt stets senkrecht zur Stromrichtung und senkrecht zum Magnetfeld. Für den Zusammenhang zwischen Stromfluss, Magnetfeld und Richtung der wirkenden Kraft gilt folgende Merkregel:
Drei-Finger-Regel:
Zeigt der Daumen der rechten Hand in Richtung der technischen Stromrichtung (von+nach-) und der Zeigefinger in Richtung des Magnetfeldes, so gibt der Mittelfinger die Richtung der wirkenden Kraft an.
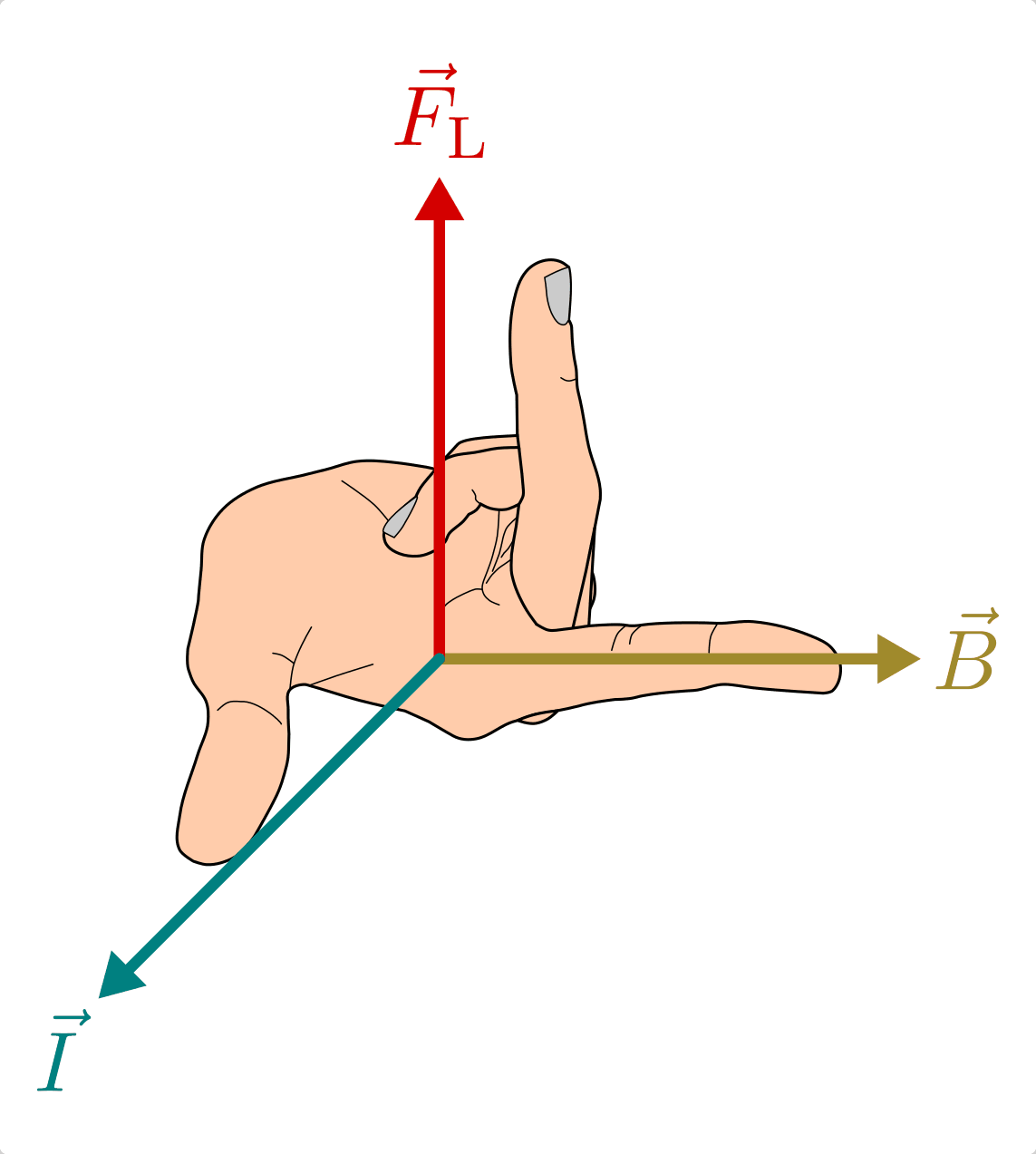
Die Drei-Finger-Regel als Merkhilfe für die Richtungen der Lorentskraft
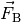 , des Magnetfeldes
, des Magnetfeldes 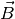 und der
technischen Stromrichtung
und der
technischen Stromrichtung 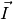 .
.
Bezeichnet man die Länge des vom Strom  durchflossenen Leiterstücks,
das sich im Magnetfeld
durchflossenen Leiterstücks,
das sich im Magnetfeld 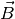 befindet, mit
befindet, mit 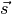 , so kann
die Lorentzkraft
, so kann
die Lorentzkraft 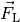 quantitativ mittels folgender
Formel berechnet werden:
quantitativ mittels folgender
Formel berechnet werden:
(3)¶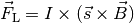
Verläuft der stromdurchflossene Leiter senkrecht zum Magnetfeld, so ist der
Betrag der Lorentzkraft gleich 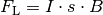 ,
andernfalls ergibt das Vektorprodukt
,
andernfalls ergibt das Vektorprodukt
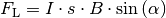 , wobei
, wobei
 den Winkel zwischen dem Leiterstück und dem Magnetfeld angibt.
Wird nicht nur ein einzelnes Leiterstück, sondern beispielsweise eine Spule mit
den Winkel zwischen dem Leiterstück und dem Magnetfeld angibt.
Wird nicht nur ein einzelnes Leiterstück, sondern beispielsweise eine Spule mit
 Windungen in das Magnetfeld eingebracht, so ergibt sich auch eine
Windungen in das Magnetfeld eingebracht, so ergibt sich auch eine
 -fache Weglänge
-fache Weglänge  und somit eine
und somit eine  -fache Kraftwirkung;
dies wird beispielsweise bei der Konstruktion von Elektromotoren genutzt.
-fache Kraftwirkung;
dies wird beispielsweise bei der Konstruktion von Elektromotoren genutzt.
Bewegung geladener Teilchen in magnetischen Feldern
Ein elektrischer Strom entspricht einem zeitlichen Transport elektrischer
Ladung. Setzt man den Zusammenhang 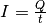 zwischen der
Stromstärke
zwischen der
Stromstärke  , der transportierten Ladungsmenge
, der transportierten Ladungsmenge 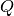 und der dafür
benötigten Zeit
und der dafür
benötigten Zeit  in die die obige Formel (3) ein, so
folgt:
in die die obige Formel (3) ein, so
folgt:
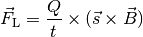
Diese Gleichung kann auch folgendermaßen geschrieben werden:
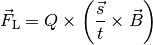
Das Verhältnis aus der Wegstrecke  und der Zeit
und der Zeit  kann als
Geschwindigkeit
kann als
Geschwindigkeit  geschrieben werden. Somit ergibt sich für ein mit
einer Ladung
geschrieben werden. Somit ergibt sich für ein mit
einer Ladung 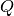 geladenes Teilchen, das sich mit der Geschwindigkeit
geladenes Teilchen, das sich mit der Geschwindigkeit
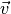 durch ein Magnetfeld mit einer Flussdichte
durch ein Magnetfeld mit einer Flussdichte 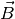 bewegt:
bewegt:
(4)¶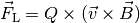
Auch in diesem Fall ergibt das Vektorprodukt einen
maximalen Wert, wenn sich das Teilchen senkrecht zum Magnetfeld bewegt;
andernfalls kann für das Vektorprodunkt 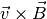 auch
auch
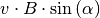 geschrieben werden, wobei
geschrieben werden, wobei  den Winkel zwischen der Bewegungsrichtung des geladenen Teilchens und der
Richtung des Magnetfelds angibt. Die obige Gleichung kann auch folgendermaßen
geschrieben werden:
den Winkel zwischen der Bewegungsrichtung des geladenen Teilchens und der
Richtung des Magnetfelds angibt. Die obige Gleichung kann auch folgendermaßen
geschrieben werden:
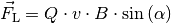
Ist 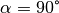 , so gilt
, so gilt 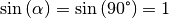 , und die Lorentz-Kraft nimmt ihren maximalen Wert
, und die Lorentz-Kraft nimmt ihren maximalen Wert
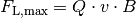 an.
an.
Anwendung: Massen-Spektrometer
Die Lorentz-Kraft kann genutzt werden, um die so genannte „spezifische Ladung“
eines Teilchens, das heißt das Verhältnis aus seiner Ladung 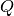 und seiner
Masse
und seiner
Masse  zu bestimmen. Hierzu lässt man das Teilchen (beziehungsweise ein
Strahl gleichartiger Teilchen) mit einer Geschwindigkeit
zu bestimmen. Hierzu lässt man das Teilchen (beziehungsweise ein
Strahl gleichartiger Teilchen) mit einer Geschwindigkeit  senkrecht zu
den Magnetfeldlinien in ein Magnetfeld eintreten.
senkrecht zu
den Magnetfeldlinien in ein Magnetfeld eintreten.
Bewegt sich ein geladenes Teilchen, beispielsweise ein Ion oder ein Elektron, in
der waagrechten Ebene und ist das Magnetfeld vertikal ausgelegt, so bleibt die
Geschwindigkeit 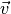 des Teilchens auch bei einer Ablenkung durch die
Lorentz-Kraft senkrecht zum Magnetfeld. Befindet sich die Anordnung in einem
Vakuum, so herrschen keine Reibungskräfte, also ist der Betrag der
Geschwindigkeit
des Teilchens auch bei einer Ablenkung durch die
Lorentz-Kraft senkrecht zum Magnetfeld. Befindet sich die Anordnung in einem
Vakuum, so herrschen keine Reibungskräfte, also ist der Betrag der
Geschwindigkeit  des Teilchens konstant. Hält man auch die magnetische
Flussdichte
des Teilchens konstant. Hält man auch die magnetische
Flussdichte 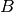 des Magnetfelds konstant, so bleibt ebenfalls der Betrag
der Lorentz-Kraft
des Magnetfelds konstant, so bleibt ebenfalls der Betrag
der Lorentz-Kraft 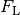 konstant.
konstant.
Die Lorentz-Kraft zwingt das geladene Teilchen durch die kontinuierliche
Ablenkung auf eine Kreisbahn. Als Gleichgewichtsbedingung müssen die dafür
notwendige Radialkraft 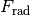 und die
Lorentz-Kraft
und die
Lorentz-Kraft 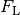 gleich groß sein:
gleich groß sein:
![F_{\mathrm{rad}} &= F_{\mathrm{L}} \\[4pt]
m \cdot \frac{v^2}{r} &= Q \cdot v \cdot B \\[4pt]](../_images/math/0b8f74d2b648123e4f0a5cad107709483758b8ff.png)
Für die spezifische Ladung 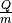 des Teilchens ergibt sich also:
des Teilchens ergibt sich also:
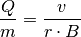
Ist die Flussdichte 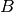 des Magnetfelds sowie die Eintrittsgeschwindigkeit
des Magnetfelds sowie die Eintrittsgeschwindigkeit
 bekannt, so kann durch eine Messung des Radius
bekannt, so kann durch eine Messung des Radius  der Kreisbahn
auf die spezifische Ladung des Teilchens geschlossen werden; eine derartige
Anordnung wird Massen-Spektrometer genannt.
der Kreisbahn
auf die spezifische Ladung des Teilchens geschlossen werden; eine derartige
Anordnung wird Massen-Spektrometer genannt.
Handelt es sich bei dem Teilchen-Strahl um Ionen mit jeweils gleicher Ladung, so
kann mit einem Massen-Spektrometer insbesondere bestimmt werden, in welchem
Verhältnis einzelne Isotope des Ions auftreten; diese haben
weitestgehend gleiche chemische und physikalische Eigenschaften, variieren
jedoch in ihrer Masse  . In einem Massen-Spektrometer werden Isotope mit
größerer Masse auf Kreisbahnen mit größerem Radius gelenkt, so dass mittels
entsprechender Detektoren die Häufigkeitsverteilung der einzelnen Isotope
gemessen werden kann.
. In einem Massen-Spektrometer werden Isotope mit
größerer Masse auf Kreisbahnen mit größerem Radius gelenkt, so dass mittels
entsprechender Detektoren die Häufigkeitsverteilung der einzelnen Isotope
gemessen werden kann.
Anwendung: Hall-Sensoren
Die Lorentz-Kraft findet auch Anwendung in nach Edwin Hall benannten „Hall-Sensoren“, die zur Messung von magnetischen Flussdichten verwendet werden können.
Ein Hall-Sensor hat prinzipiell folgenden Aufbau:
Längs durch ein dünnes Halbleiter-Plättchen lässt man, indem man an den zwei entsprechenden Anschluss-Stellen eine konstante elektrische Spannung anlegt, einen elektrischen Strom fließen. Hierdurch bewegen sich also Elektronen mit einer bestimmten Geschwindigkeit
 in Längsrichtung durch das
Plättchen.
in Längsrichtung durch das
Plättchen.Tritt senkrecht durch die Querschnittsfläche des Plättchens ein magnetischer Fluss
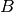 hindurch, so erfahren die Elektronen gemäß der Gleichung
(4) eine Lorentz-Kraft und somit eine
Ablenkung entlang der Breite des Plättchens. Für den Betrag der ablenkenden
Kraft gilt also:
hindurch, so erfahren die Elektronen gemäß der Gleichung
(4) eine Lorentz-Kraft und somit eine
Ablenkung entlang der Breite des Plättchens. Für den Betrag der ablenkenden
Kraft gilt also: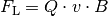
Durch die Ablenkung der Elektronen und den Verbleib der positiv geladenen Atomkerne baut sich entlang der Breite des Plättchens ein elektrisches Feld auf. Das elektrische Feld übt auf die Elektronen eine Kraft in die umgekehrte Richtung aus, das sich die angehäuften Elektronen gegenseitig abstoßen. Für den Betrag der elektrischen Kraft
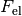 gilt:
gilt: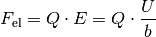
Hierbei wurde der Zusammenhang
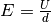 genutzt, der die
elektrische Feldstärke
genutzt, der die
elektrische Feldstärke 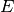 eines Plattenkondensators in Abhängigkeit von der anliegenden Spannung
eines Plattenkondensators in Abhängigkeit von der anliegenden Spannung  und dem Plattenabstand
und dem Plattenabstand 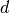 beschreibt. Im obigen Fall entspricht der
Plattenabstand gerade der Breite
beschreibt. Im obigen Fall entspricht der
Plattenabstand gerade der Breite 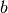 des Plättchens.
des Plättchens.
Die Elektronen in einem Hall-Sensor werden so lange durch die Lorentz-Kraft abgelenkt, bis sich durch das sich aufbauende elektrische Feld eine gleich große, entgegengesetzt gerichtete Kraft einstellt. Ist dies der Fall, so herrscht folgendes Gleichgewicht:
![F_{\mathrm{L}} &= F_{\mathrm{el}} \\[4pt]
Q \cdot v \cdot B &= Q \cdot \frac{U_{\mathrm{H}}}{b}](../_images/math/b28215c264cbdc2194b0359ab48ec12036769404.png)
Die sich im Gleichgewichtsfall einstellende elektrische Spannung wird
„Hall-Spannung“ 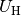 genannt; sie kann an entsprechenden
Anschlüssen entlang der Breitseite des Plättchens abgegriffen und gemessen
werden. Für die Hall-Spannung gilt gemäß der obigen Gleichung:
genannt; sie kann an entsprechenden
Anschlüssen entlang der Breitseite des Plättchens abgegriffen und gemessen
werden. Für die Hall-Spannung gilt gemäß der obigen Gleichung:
(5)¶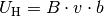
Kennt man die Geschwindigkeit der Elektronen, die sich je nach
Halbleiter-Material beim Stromfluss durch das Plättchen einstellt, so kann durch
eine Messung der Hall-Spannung unmittelbar die magnetische Flussdichte 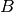 eines externen Magnetfelds berechnet werden.
eines externen Magnetfelds berechnet werden.
Hall-Sensoren haben in der Praxis vielerlei Anwendungen, insbesondere weil sie sehr resistent gegen Wasser, Schmutz und Erschütterungen sind. Sie werden beispielsweise in so genannten „Stromzangen“ zur berührungslosen Messung von Strömen in elektrischen Leitern sowie in Leitungssuchgeräten eingesetzt; in beiden Fällen wird ausgenutzt, dass elektrische Ströme in Leitern ein Magnetfeld hervorrufen, das mit Hall-Sensoren gemessen werden kann. Ebenso werden Hall-Sensoren zur Drehzahlmessung in Fahrzeugen und Turbinen eingesetzt; in die am Hall-Sensor vorbei rotierenden Objekte müssen lediglich kleine Magnete verbaut werden, die bei jeder Umdrehung am Sensor ein kurzes Spannungs-Signal bewirken, der mit einer geeigneten Mess-Schaltung registriert werden kann.
Elektromagnetische Induktion¶
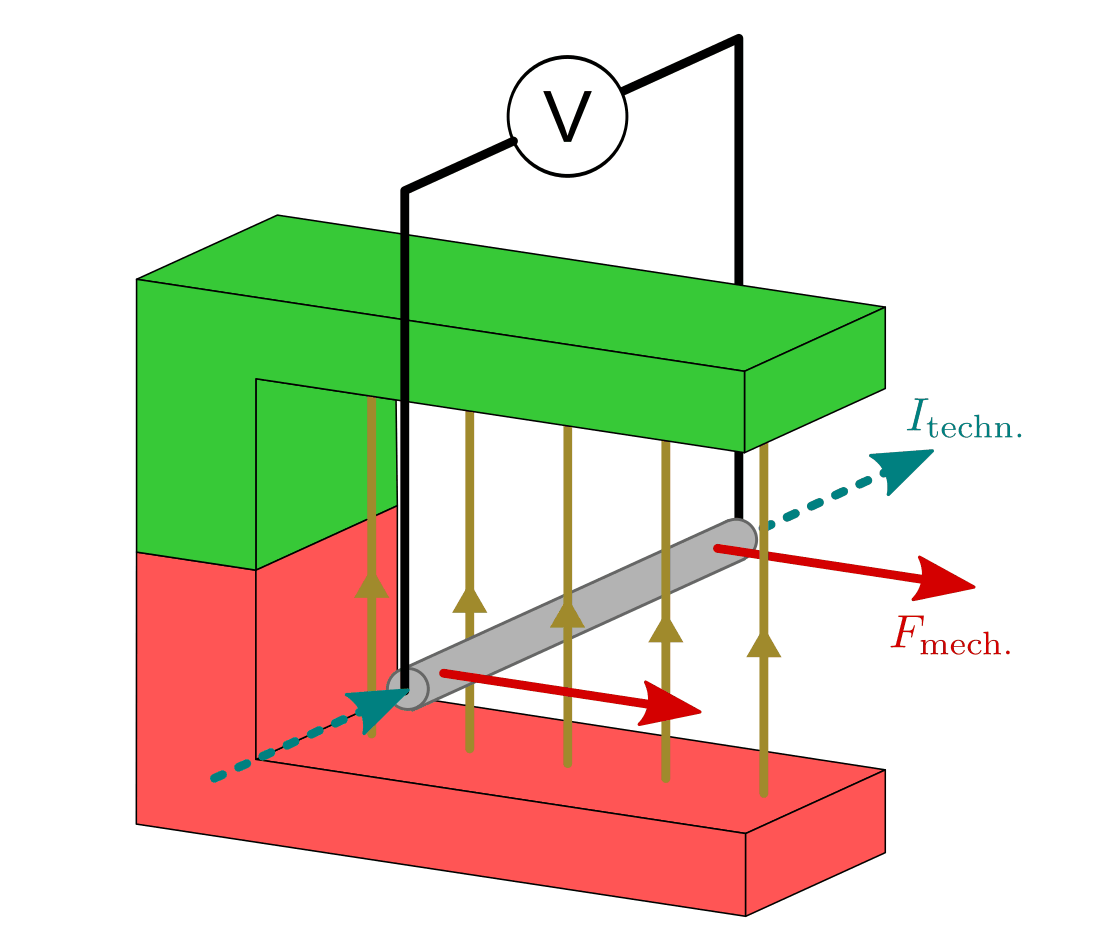
Bewegt man ein Stück Metall senkrecht zu den Feldlinien eines homogenen Magnetfelds, so bewirkt die Lorentz-Kraft im Inneren des Leiters eine Verschiebung der Elektronen senkrecht zur Bewegungsrichtung und ebenfalls senkrecht zur Richtung des Magnetfelds. Da sich nur die freien Elektronen, jedoch nicht die positiv geladenen Atomkerne bewegen, baut sich im Inneren des Metalls zwischen den beiden Enden ein elektrisches Feld beziehungsweise eine elektrische Spannung auf.
Dieser Vorgang wird elektromagnetische Induktion genannt. Schließt man ein Messgerät oder einen Verbraucher (beispielsweise eine kleine Glühbirne) an die Enden des Leiters an, so kann prinzipiell die induzierte Spannung gemessen beziehungsweise als Stromquelle genutzt werden. Bei einem einzelnen kurzen Leiterstück ergeben sich jedoch nur sehr geringe Spannungswerte im Milivolt-Bereich; größere Spannungs- beziehungsweise Stromwerte ergeben sich wiederum, wenn das einzelne Leiterstück durch eine Spule mit möglichst vielen Windungen ersetzt wird.
In der obigen Abbildung ist auch die technische Stromrichtung eingezeichnet, die sich bei einer Bewegung der Leiterschaukel durch die angegebene mechanische Kraft ergibt (Lorentz-Kraft beziehungsweise Drei-Finger-Regel). Ist kein Verbraucher beziehungsweise Messgerät angeschlossen, so baut sich in gleicher Richtung ein elektrisches Feld auf, bedingt durch Ladungsverschiebungen im Inneren der Leiterschaukel. Im Gleichgewichtsfall wird die Lorentz-Kraft, welche die Elektronen im Inneren des durch das Magnetfeld bewegten Leiterstücks erfahren, durch das sich resultierende elektrische Feld ausgeglichen:
![F_{\mathrm{L}} &= F_{\mathrm{el}} \\[4pt]
Q \cdot v \cdot B &= Q \cdot \frac{U_{\mathrm{i}}}{d}](../_images/math/90190d3c573d38b47ae681936c38f2e86bae85c1.png)
Die sich einstellende Spannung wird Induktionsspannung 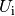 genannt,
genannt, 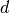 bezeichnet die Länge des Leiterstücks, das sich im Magnetfeld
befindet. Wird die obige Gleichung nach
bezeichnet die Länge des Leiterstücks, das sich im Magnetfeld
befindet. Wird die obige Gleichung nach 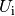 aufgelöst, so
ergibt sich:
aufgelöst, so
ergibt sich:
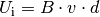
Es tritt nur dann eine Induktionsspannung auf, wenn der Leiter mit einer
Geschwindigkeit  senkrecht zum Magnetfeld bewegt wird. Hat die
Geschwindigkeit den Wert Null oder verläuft die Bewegung parallel zu den
Magnetfeldlinien, so ist die induzierte Spannung gleich Null.
senkrecht zum Magnetfeld bewegt wird. Hat die
Geschwindigkeit den Wert Null oder verläuft die Bewegung parallel zu den
Magnetfeldlinien, so ist die induzierte Spannung gleich Null.
Das Faraday’sche Induktionsgesetz¶
Um eine allgemeinere Formel zur Beschreibung der einer elektromagnetischen
Induktion auftretenden Spannung 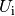 aufstellen zu können, ist
es sinnvoll, eine neue Größe
aufstellen zu können, ist
es sinnvoll, eine neue Größe 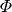 zu definieren, die man als
„magnetischen Fluss“ bezeichnet:
zu definieren, die man als
„magnetischen Fluss“ bezeichnet:
(6)¶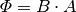
Zwischen dem magnetischen Fluss 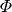 und der magnetischen Flussdichte
und der magnetischen Flussdichte
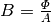 besteht ein ähnlicher Zusammenhang wie zwischen
der Stromstärke
besteht ein ähnlicher Zusammenhang wie zwischen
der Stromstärke  und der Stromdichte
und der Stromdichte 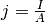 : Die
letzteren Größen geben jeweils die Flächendichte der Bezugsgröße an. Bei der
magnetischen Flussdichte geht es allerdings nicht um Ladungsträger, die durch
eine bestimmte Fläche hindurch wandern, sondern um die Anzahl an Feldlinien,
welche durch diese hindurchgehen. Der magnetische Fluss beschreibt entsprechend
der Menge an Feldlinien, welche durch eine Fläche
: Die
letzteren Größen geben jeweils die Flächendichte der Bezugsgröße an. Bei der
magnetischen Flussdichte geht es allerdings nicht um Ladungsträger, die durch
eine bestimmte Fläche hindurch wandern, sondern um die Anzahl an Feldlinien,
welche durch diese hindurchgehen. Der magnetische Fluss beschreibt entsprechend
der Menge an Feldlinien, welche durch eine Fläche  verlaufen.
verlaufen.
Ist der magnetische Fluss 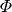 durch eine Fläche zeitlich konstant,
so ist die induzierte Spannung
durch eine Fläche zeitlich konstant,
so ist die induzierte Spannung 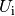 gleich Null. Ändert sich
hingegen der magnetische Fluss
gleich Null. Ändert sich
hingegen der magnetische Fluss 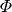 , indem man wahlweise die Stärke
, indem man wahlweise die Stärke
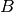 der magnetischen Flussdichte und/oder die Größe der vom Magnetfeld
durchfluteten Fläche
der magnetischen Flussdichte und/oder die Größe der vom Magnetfeld
durchfluteten Fläche  ändert, so wird eine Induktionsspannung
ändert, so wird eine Induktionsspannung
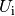 erzeugt, die umso größer ist, je schneller diese Änderung
erfolgt. Als Zusammenhang ergibt sich somit für die Induktionsspannung in einer
Leiterschleife:
erzeugt, die umso größer ist, je schneller diese Änderung
erfolgt. Als Zusammenhang ergibt sich somit für die Induktionsspannung in einer
Leiterschleife:
(7)¶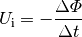
Diese Gesetzmäßigkeit, wonach die in einer Leiterschleife induzierte Spannung gleich der zeitlichen Änderung des magnetischen Flusses ist, wurde als erstes im Jahr 1831 von Michael Faraday entdeckt.
Beispiele:
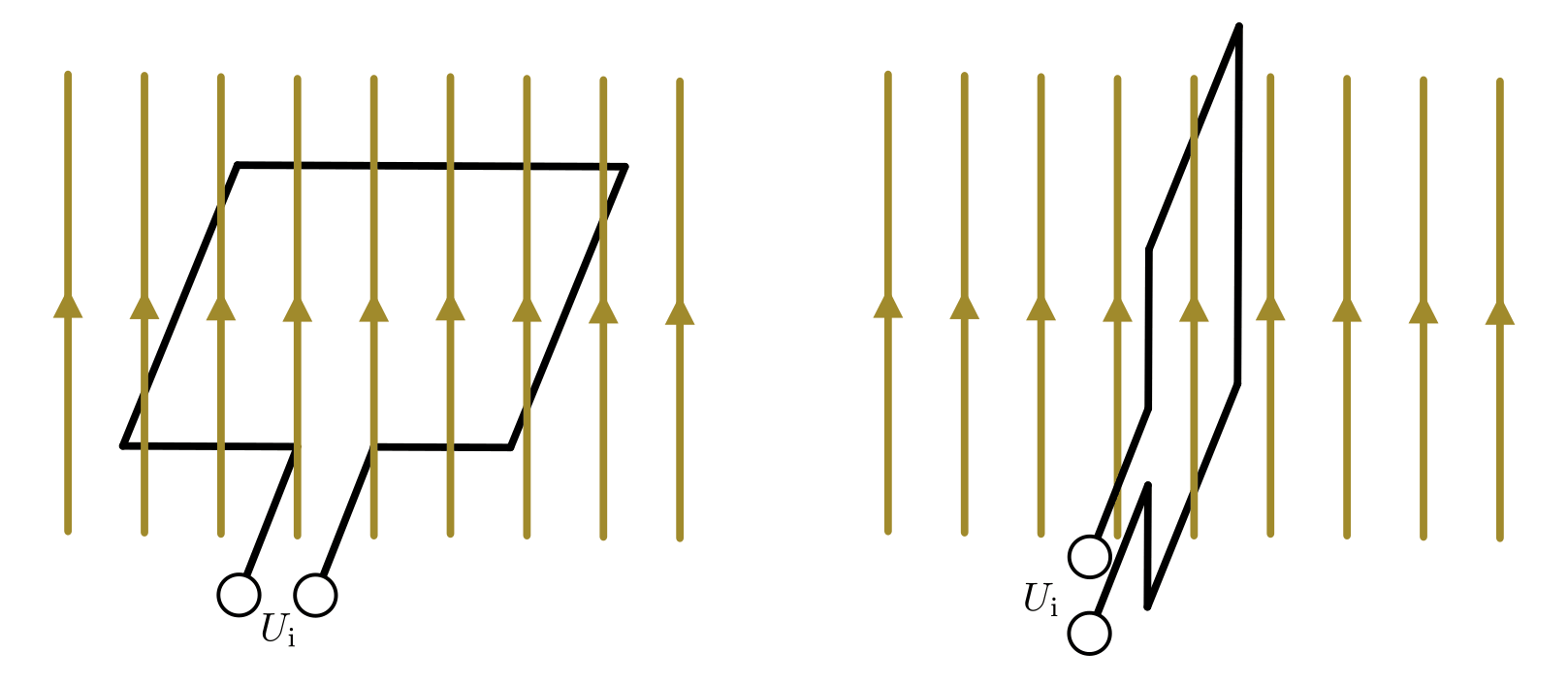
In einem homogenen und zeitlich konstanten Magnetfeld kann eine Änderung der vom Magnetfeld durchfluteten Fläche
 einerseits durch ein Verschieben
der Leiterschleife in das Magnetfeld hinein beziehungsweise aus dem Magnetfeld
heraus bewirkt werden; andererseits kann der gleiche Effekt, wie in der
folgenden Abbildung zu sehen ist, auch durch eine Rotation der Leiterschleife
im Magnetfeld bewirkt werden.
einerseits durch ein Verschieben
der Leiterschleife in das Magnetfeld hinein beziehungsweise aus dem Magnetfeld
heraus bewirkt werden; andererseits kann der gleiche Effekt, wie in der
folgenden Abbildung zu sehen ist, auch durch eine Rotation der Leiterschleife
im Magnetfeld bewirkt werden.Bewegt man durch eine ruhende Leiterschleife einen Stabmagneten, dessen magnetische Flussdichte nicht homogen ist (sondern zu den Polen hin zunimmt), so spürt die Leiterschleife ein sich zeitlich änderndes Magnetfeld. Auch hierbei wird also eine (wenn auch sehr geringe) Spannung induziert.
Die beiden oben beschriebenen Möglichkeiten zum Erwirken einer
Induktionsspannung können optimiert werden, indem man statt einer einzelnen
Leiterschleife eine aus möglichst vielen Windungen bestehende Spule verwendet.
Für die Induktionsspannung einer Spule mit 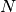 Windungen gilt:
Windungen gilt:
(8)¶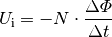
Die Lenzsche Regel
In den obigen Gleichung (7) und
(8) zur Beschreibung der Induktionsspannung
steht jeweils vor der zeitlichen Änderung 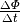 ein Minus-Zeichen. Dies ist eine Folge einer von Emil Lenz entdeckten Gesetzmäßigkeit, wonach
die Induktionsspannung stets ihrer Ursache entgegenwirkt.
ein Minus-Zeichen. Dies ist eine Folge einer von Emil Lenz entdeckten Gesetzmäßigkeit, wonach
die Induktionsspannung stets ihrer Ursache entgegenwirkt.
Die Ursache für die Induktionsspannung ist letztlich die Lorentz-Kraft, welche im Inneren der bewegten Leiterschleife(n) eine Verschiebung der Elektronen und somit ein elektrisches Feld bewirkt. Durch dieses Feld werden die Elektronen allerdings nicht weiter beschleunigt (was ein Perpetuum mobile zur Folge hätte), sondern vielmehr abgebremst.
… to be continued …
Hinweis
Zu diesem Abschnitt gibt es Experimente und Übungsaufgaben.