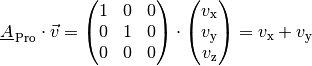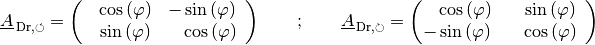Matrizen¶
Bei einer Matrix handelt es sich um eine
rechteckige Anordnungen mehrerer Zahlen. Hat eine Matrix 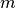 Zeilen und
Zeilen und
 Spalten, so sagt man, die Matrix sei vom Typ
Spalten, so sagt man, die Matrix sei vom Typ 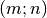 . Eine
solche Matrix hat allgemein folgende Gestalt:
. Eine
solche Matrix hat allgemein folgende Gestalt:
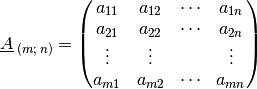
In der Literatur werden Matrizen häufig auch durch fettgedruckte Großbuchstaben
bezeichnet, in der Praxis werden die Großbuchstaben hingegen üblicherweise
unterstrichen. Die in einer Matrix 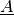 stehenden Zahlen werden
allgemein Elemente oder Komponenten
stehenden Zahlen werden
allgemein Elemente oder Komponenten 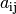 der Matrix genannt,
wobei
der Matrix genannt,
wobei  den Zeilenindex (eine Zahl zwischen
den Zeilenindex (eine Zahl zwischen 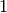 und
und  ) und
) und
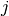 den Spaltenindex (eine Zahl zwischen
den Spaltenindex (eine Zahl zwischen 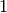 und
und  )
bezeichnet. Schreibt man
)
bezeichnet. Schreibt man 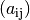 in runden Klammern, so ist
damit die Gesamtheit aller Komponenten, also wiederum die ganze Matrix gemeint.
in runden Klammern, so ist
damit die Gesamtheit aller Komponenten, also wiederum die ganze Matrix gemeint.
Spezielle Matrizen
Matrizen können sowohl hinsichtlich der Zahlenwerte ihrer Komponenten als auch
hinsichtlich ihrer Form Besonderheiten aufweisen: Beispielsweise werden
Matrizen, die ausschließlich Nullen als Werte enthalten, Nullmatrizen genannt.
Andererseits können auch gewöhnliche Vektoren als spezielle Matrizen mit einer
Spaltenzahl von 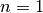 aufgefasst werden:
aufgefasst werden:
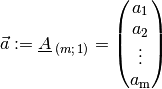
Matrizen, die hingegen nur eine Zeilenzahl von 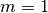 haben, werden
entsprechend Zeilenvektoren genannt:
haben, werden
entsprechend Zeilenvektoren genannt:
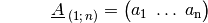
Ein Zeilenvektor, der die gleichen Elemente hat wie ein Spaltenvektor
 , wird häufig auch mit
, wird häufig auch mit 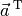 bezeichnet. Das
hochgestellte
bezeichnet. Das
hochgestellte 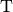 bedeutet dabei „transponiert“. Allgemein kann zu jeder
Matrix
bedeutet dabei „transponiert“. Allgemein kann zu jeder
Matrix 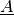 eine transponierte Matrix
eine transponierte Matrix 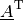 gebildet werden, indem man die Zeilen und Spalten der Matrix vertauscht:
gebildet werden, indem man die Zeilen und Spalten der Matrix vertauscht:
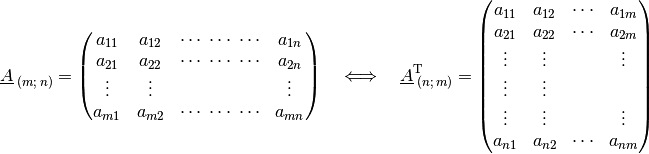
Beim Transponieren einer Matrix bleiben also nur diejenigen Komponenten unverändert, die auf der von links oben nach rechts unten verlaufenden „Hauptdiagonalen“ liegen; alle anderen Einträge werden an dieser Diagonalen gespiegelt. Bleibt eine Matrix beim Transponieren unverändert, so nennt man sie symmetrisch.
Eine weitere Sonderstellung haben quadratische Matrizen, für deren Zeilen- wie
auch Spaltenanzahl  gilt. Für jede derartige Matrix
gilt. Für jede derartige Matrix
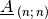 lässt sich eine so genannte Diagonalmatrix
lässt sich eine so genannte Diagonalmatrix
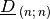 angeben, bei der alle Komponenten, die nicht
auf der Hauptdiagonalen liegen, gleich Null sind:
angeben, bei der alle Komponenten, die nicht
auf der Hauptdiagonalen liegen, gleich Null sind:

Eine Sonderform einer Diagonalmatrix ist eine so genannte Einheitsmatrix, bei
der alle Elemente auf der Hauptdiagonalen den Wert 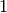 haben.
haben.
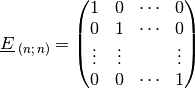
Eine Gleichheit zweier Matrizen liegt nur dann vor, wenn beide die gleiche Form haben und die Werte aller ihrer Komponenten identisch sind. Es muss also gelten:
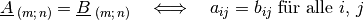
Die Wirkungsweise von Matrizen auf geometrische Objekte wird im übernächsten Abschnitt beschrieben; im nächsten Abschnitt werden zunächst einige grundlegende Rechenregeln für den Umgang mit Matrizen vorgestellt.
Rechenregeln für Matrizen¶
Die wichtigsten Rechenoperationen für Matrizen sind die Addition zweier Matrizen sowie die Multiplikation einer Matrix mit einer Zahl, einem Vektor oder einer anderen Matrix. Die Rechenregeln für Matrizen basieren auf den üblichen Grundrechenregeln der Arithmetik; man muss diese lediglich in geordneter Weise auf „mehr“ Zahlen angewenden.
Addition zweier Matrizen
Haben zwei Matrizen die gleiche Form, so können sie addiert beziehungsweise subtrahiert werden, indem die jeweils an gleicher Stelle stehenden Komponenten addiert beziehungsweise subtrahiert werden:
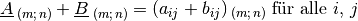
Das Resultat einer Addition beziehungsweise Subtraktion ist wiederum eine Matrix, welche die gleiche Form hat wie jede der beiden ursprünglichen Matrizen.
Beispiel:
Welches Ergebnis liefert die Addition der folgenden beiden Matrizen?
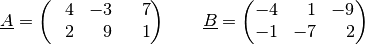
Bei der Matrizen-Addition werden die einzelnen Komponenten beider Matrizen addiert:
![\underline{A} + \underline{B} &= \begin{pmatrix}
\phantom{+}4 & -3 & \phantom{+}7 \\
\phantom{+}2 & \phantom{+}9 & \phantom{+}1 \\
\end{pmatrix} +
\begin{pmatrix}
-4 & \phantom{+}1 & -9 \\
-1 & -7 & \phantom{+}2 \\
\end{pmatrix} \\[4pt] &=
\begin{pmatrix}
\big(4+(-4)\big) & \big( (-3) + \phantom{+}1\big) & \big( 7 + (-9)\big) \\
\big(2 + (-1)\big) & \big(\phantom{+}9 + (-7)\big) & \big( 1 + \phantom{+}2 \phantom{+}\big) \\
\end{pmatrix} =
\begin{pmatrix}
0 & -2 & -2 \\
1 & \phantom{+}2 & \phantom{+}3
\end{pmatrix}](../_images/math/b2a9a7161b446d04f93fde2405de81175640607a.png)
Da die Addition beziehungsweise Subtraktion komponentenweise nach den gleichen Rechenregeln wie mit gewöhnlichen Zahlen erfolgt, gilt auch für die Addition beziehungsweise Subtraktion das Kommutativ- und Assoziativgesetz :
(1)¶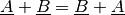
(2)¶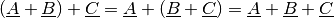
Multiplikation einer Matrix mit einer Zahl
Die Multiplikation einer Matrix mit einer reellen Zahl (einem so genannten
„Skalar“) erfolgt ebenfalls komponentenweise: Jedes Element der Matrix
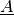 wird mit dem Wert des Skalars
wird mit dem Wert des Skalars  multipliziert. Man
kann also schreiben:
multipliziert. Man
kann also schreiben:
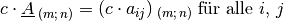
Das Resultat einer ist wiederum eine Matrix, welche die gleiche Form hat wie die ursprüngliche Matrix.
Beispiel:
Welches Ergebnis erhält man, wenn man folgende Matrix mit
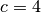 multipliziert?
multipliziert?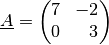
Bei der Multiplikation einer Matrix mit einer Zahl werden alle Komponenten der Matrizen mit dieser Zahl multipliziert:
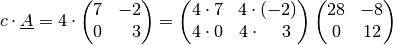
Auch für die Multiplikation einer Matrix mit einer Zahl gelten das Kommutativ- und Assoziativgesetz:
(3)¶
(4)¶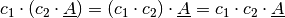
Zudem gilt das Distributivgesetz in gewohnter Form:
(5)¶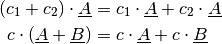
Multiplikation eines Zeilen- mit einem Spaltenvektor
Zur Herleitung einer Rechenregel für die Multiplikation zweier Matrizen wird zunächst von der skalaren Multiplikation eines Zeilenvektors mit einem Spaltenvektor ausgegangen. Wie bei einem gewöhnlichen Skalarprodukt zweier Vektoren werden dabei die einzelnen Komponenten des Zeilen- und des Spaltenvektors miteinander multipliziert, und die sich dabei ergebenden Teilergebnisse schließlich summiert.
(6)¶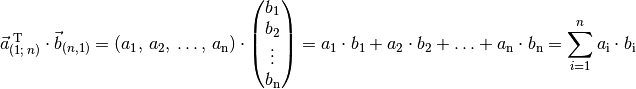
Damit eines solches Produkt möglich ist, muss der Zeilenvektor ebenso viele Komponenten haben wie der Spaltenvektor. Das Ergebnis des Produkts ist dann eine gewöhnliche Zahl (ein Skalar).
Beispiel:
Welches Ergebnis erhält man, wenn man den Zeilenvektor
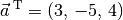 mit dem Spaltenvektor
mit dem Spaltenvektor
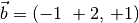 multipliziert?
multipliziert?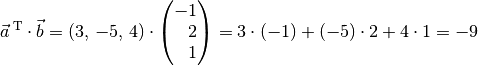
Das Produkt liefert somit den Wert
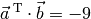
Multiplikation einer Matrix mit einem Vektor
Multipliziert man nun nicht nur einen Zeilenvektor mit  Komponenten,
sondern eine
Komponenten,
sondern eine  -spaltige Matrix mit einem Spaltenvektor der Länge
-spaltige Matrix mit einem Spaltenvektor der Länge
 , so wird nach der obigen Regel
(6) für jede Zeile der Matrix ein
Skalarprodukt mit dem Spaltenvektor gebildet. Hat die Matrix
, so wird nach der obigen Regel
(6) für jede Zeile der Matrix ein
Skalarprodukt mit dem Spaltenvektor gebildet. Hat die Matrix 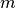 Zeilen,
so erhält man folglich
Zeilen,
so erhält man folglich 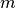 einzelne Ergebnisse. Diese werden als
Komponenten in einen neuen Spaltenvektor der Länge
einzelne Ergebnisse. Diese werden als
Komponenten in einen neuen Spaltenvektor der Länge 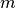 geschrieben.
geschrieben.
![\begin{array}{c|c}
\underline{A} \cdot \vec{b} &
\begin{pmatrix}
\; b_1 \; \\
b_2 \\
\vdots \\
b_{n} \\
\end{pmatrix} \\ \midrule
\begin{pmatrix}
a_{11} & a_{12} & \ldots & a_{1n} \\
a_{21} & a_{22} & \ldots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{m1} & a_{m2} & \ldots & a_{mn} \\
\end{pmatrix} &
\begin{pmatrix}
\sum_{i=1}^{n} a_{\mathrm{1i}} \cdot b_{\mathrm{i}} \\[4pt]
\sum_{i=1}^{n} a_{\mathrm{2i}} \cdot b_{\mathrm{i}} \\[4pt]
\vdots \\
\sum_{i=1}^{n} a_{\mathrm{mi}} \cdot b_{\mathrm{i}} \\
\end{pmatrix}
\end{array}](../_images/math/598808870ae559fbda2f8be308524c6e15cae967.png)
Beispiel:
Welches Ergebnis erhält man, wenn man die folgende Matrix
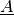 mit dem folgenden Vektor
mit dem folgenden Vektor  multipliziert?
multipliziert?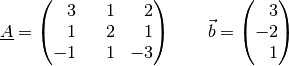
Für die Multiplikation der Matrix
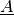 mit dem Vektor
mit dem Vektor
 gilt nach obigem Schema:
gilt nach obigem Schema: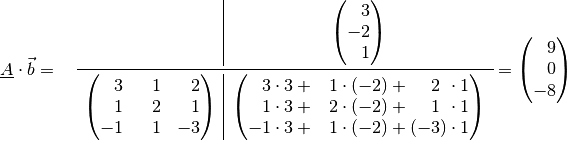
Ein Produkt einer Matrix mit einem Vektor kann nur dann gebildet werden, wenn die Anzahl an Spalten der Matrix mit der Anzahl an Zeilen des Vektors übereinstimmt; andernfalls ist die Multiplikation nicht definiert.
Multiplikation zweier Matrizen
Beim so genannten „Falk-Schema“, wie es in der obigen Abbildung dargestellt ist,
werden die zu multiplizierenden Matrizen beziehungsweise Vektoren tabellenartig
aufgelistet.[1] Die Auswertung erfolgt allgemein nach folgender Regel:
Multipliziert man die  -te Zeile der linken Matrix mit der
-te Zeile der linken Matrix mit der 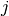 -ten
Spalter der rechten Matrix, so erhält man die Komponente der Ergebnis-Matrix,
die dort in der
-ten
Spalter der rechten Matrix, so erhält man die Komponente der Ergebnis-Matrix,
die dort in der  -ten Zeile und
-ten Zeile und 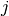 -ten Spalte steht.
-ten Spalte steht.
Das Falk-Schema kann also einfach auf die Multiplikation zweier Matrizen ausgeweitet werden: Hierbei wird jeweils an der Stelle, wo sich eine Zeile der linken Matrix mit einer Spalte der rechten Matrix überkreuzt, das entsprechende Skalarprodukt eingetragen.
![\begin{array}{c|c}
\underline{A} \cdot \underline{B} &
\begin{pmatrix}
\phantom{.}\quad b_{11} \;\qquad & \qquad\qquad b_{12} & \;\qquad \cdots \qquad & \qquad b_{\mathrm{1p}} \quad\phantom{.}\\[6pt]
\phantom{.}\quad b_{21} \;\qquad & \qquad\qquad b_{22} & \;\qquad \cdots \qquad & \qquad b_{\mathrm{2p}} \quad\phantom{.}\\[6pt]
\phantom{.}\quad \vdots \;\qquad & \qquad\qquad \vdots & \;\qquad \ddots \qquad & \qquad \vdots \quad\phantom{.}\\[6pt]
\phantom{.}\quad b_{\mathrm{n1}} \qquad & \qquad\qquad b_{\mathrm{n2}} & \;\qquad \cdots \qquad & \qquad b_{\mathrm{np}} \quad\phantom{.}\\
\end{pmatrix} \\ \midrule
\begin{pmatrix}
a_{11} & a_{12} & \ldots & a_{\mathrm{1n}} \\[6pt]
a_{21} & a_{22} & \ldots & a_{\mathrm{2n}} \\[6pt]
\vdots & \vdots & \ddots & \vdots \\[6pt]
a_{\mathrm{m1}} & a_{\mathrm{m2}} & \ldots & a_{\mathrm{mn}} \\
\end{pmatrix} &
\begin{pmatrix}
\sum_{i=1}^{n} a_{\mathrm{1i}} \cdot b_{\mathrm{1i}} & \sum_{i=1}^{n}
a_{\mathrm{1i}} \cdot b_{\mathrm{2i}} & \cdots & \sum_{i=1}^{n}
a_{\mathrm{1i}} \cdot b_{\mathrm{pi}} \\[6pt]
\sum_{i=1}^{n} a_{\mathrm{2i}} \cdot b_{\mathrm{1i}} & \sum_{i=1}^{n}
a_{\mathrm{2i}} \cdot b_{\mathrm{2i}} & \cdots & \sum_{i=1}^{n} a_{\mathrm{2i}}
\cdot b_{\mathrm{pi}} \\[6pt]
\vdots & \vdots & \ddots & \vdots \\[6pt]
\sum_{i=1}^{n} a_{\mathrm{mi}} \cdot b_{\mathrm{1i}} & \sum_{i=1}^{n}
a_{\mathrm{mi}} \cdot b_{\mathrm{2i}} & \cdots & \sum_{i=1}^{n}
a_{\mathrm{mi}} \cdot b_{\mathrm{pi}} \\
\end{pmatrix}
\end{array}](../_images/math/e83a35d55e01357b90cb527941e94e96d23df095.png)
Auch in diesem Fall ist das Produkt nur dann definiert, wenn die die Anzahl an
Spalten der linken Matrix mit der Anzahl an Zeilen des Vektors übereinstimmt.
Hat die linke Matrix die Form 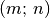 und die rechte Matrix die Form
und die rechte Matrix die Form
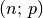 , so erhält man als Ergebnis eine neue Matrix der Form
, so erhält man als Ergebnis eine neue Matrix der Form
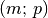 . Multipliziert man zwei quadratische Matrizen mit gleicher
Zeilen- beziehungsweise Spaltenanzahl, so ist die Form der resultierenden Matrix
mit der Form der beiden ursprünglichen Matrizen identisch.
. Multipliziert man zwei quadratische Matrizen mit gleicher
Zeilen- beziehungsweise Spaltenanzahl, so ist die Form der resultierenden Matrix
mit der Form der beiden ursprünglichen Matrizen identisch.
Beispiel:
Welches Ergebnis erhält man, wenn man die beiden folgenden Matrizen miteinander multipliziert?
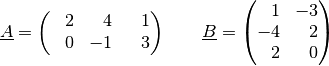
Für die Multiplikation der beiden Matrizen
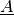 und
und
 gilt nach dem obigen Schema:
gilt nach dem obigen Schema: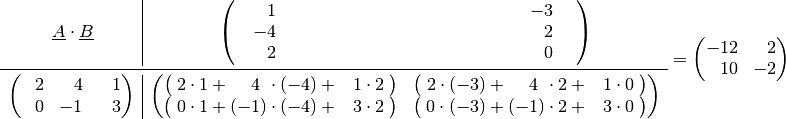
Die Bedingung, dass bei der Multiplikation zweier Matrizen auf zueinander passende Spalten- und Zeilenanzahlen geachtet werden muss, zeigt bereits, dass bei diesem Rechenvorgang die Reihenfolge der Faktoren von Bedeutung ist:
- Multipliziert man eine Matrix der Form
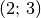 mit einer Matrix der
Form
mit einer Matrix der
Form  , so ergibt sich eine Matrix der Form
, so ergibt sich eine Matrix der Form 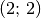 .
. - Multipliziert man eine Matrix der Form
 mit einer Matrix der
Form
mit einer Matrix der
Form 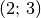 , so ergibt sich eine Matrix der Form
, so ergibt sich eine Matrix der Form 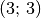 .
.
Für die Multiplikation zweier Matrizen gilt folglich im Allgemeinen Kommutativgesetz der Multiplikation nicht :
(7)¶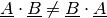
Für die Multiplikation zweier Matrizen gilt allerdings das Assoziativgesetz:
(8)¶
Auch das Distributivgesetz gilt für die Multiplikation zweier Matrizen in folgender Form:
(9)¶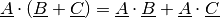
Zusätzlich gilt, dass bei jedem Produkt einer Matrix 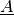 mit
einer entsprechenden Nullmatrix
mit
einer entsprechenden Nullmatrix 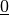 wiederum eine Nullmatrix
entsteht (da jedes einzelnen Skalarprodukt den Wert Null hat). Multipliziert man
hingegen eine beliebige Matrix
wiederum eine Nullmatrix
entsteht (da jedes einzelnen Skalarprodukt den Wert Null hat). Multipliziert man
hingegen eine beliebige Matrix 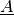 mit einer Einheitsmatrix
mit einer Einheitsmatrix
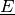 , so erhält man die ursprüngliche Matrix
, so erhält man die ursprüngliche Matrix
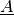 als Ergebnis. Es gilt also (in diesem Fall sogar
unabhängig von der Reihenfolge der Faktoren):
als Ergebnis. Es gilt also (in diesem Fall sogar
unabhängig von der Reihenfolge der Faktoren):
(10)¶![\underline{A} \cdot \underline{0} = \underline{0} \cdot \underline{A} &=
\underline{0} \\[4pt]
\underline{A} \cdot \underline{E} = \underline{E} \cdot \underline{A} &=
\underline{E} \\[4pt]](../_images/math/cf6b0d0a2d08106a6a16fae91aa3ea5e800fe514.png)
Eine Division zweier Matrizen ist nicht definiert.
Wirkungsweise von Matrizen¶
Die Wirkungsweise von Matrizen lässt sich gut veranschaulichen, wenn man einzelne Vektoren in einem ebenen Koordinatensystem betrachtet und verschiedene Arten von Matrizen auf diese anwendet.
Da es in einem ebenen Koordinatensystem nur zweidimensionale Objekte gibt,
benötigen die jeweiligen (Orts-)Vektoren nur zwei Komponenten ( und
und
 ); die für ein solches System relevanten Matrizen haben entsprechend
ebenfalls nur
); die für ein solches System relevanten Matrizen haben entsprechend
ebenfalls nur  Komponenten.
Komponenten.
Skalierungsmatrizen
Eine Skalierungsmatrix hat für ein zweidimensionales Koordinatensystem folgende Form:
(11)¶
Hierbei ist  ein beliebiger Zahlenwert.
ein beliebiger Zahlenwert.
Multipliziert man eine derartige Matrix mit dem Ortsvektor eines Punktes, so
erhält man als Resultat wiederum einen Ortsvektor mit gleicher Richtung; dessen
Länge beträgt allerdings das 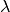 -fache des ursprünglichen
Ortsvektors.
-fache des ursprünglichen
Ortsvektors.
Beispiele:
Wird eine Skalierungsmatrix
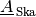 mit
mit
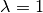 mit einem Vektor multipliziert, so bleibt dieser
unverändert. Dies soll am Beispiel des Punktes
mit einem Vektor multipliziert, so bleibt dieser
unverändert. Dies soll am Beispiel des Punktes 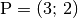 beziehungsweise des zugehörigen Ortsvektors
beziehungsweise des zugehörigen Ortsvektors 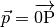 gezeigt werden:
gezeigt werden: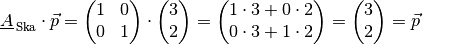
Der Vektor
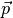 wird somit durch die Einheits-Matrix nicht verändert.
wird somit durch die Einheits-Matrix nicht verändert.Wird eine Skalierungsmatrix
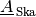 mit
mit
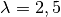 mit einem Vektor multipliziert, so wird dieser um den
Faktor
mit einem Vektor multipliziert, so wird dieser um den
Faktor 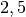 gestreckt. Dies soll am Beispiel eines Rechtecks gezeigt
werden, dessen Eckpunkte folgende Koordinaten haben:
gestreckt. Dies soll am Beispiel eines Rechtecks gezeigt
werden, dessen Eckpunkte folgende Koordinaten haben:
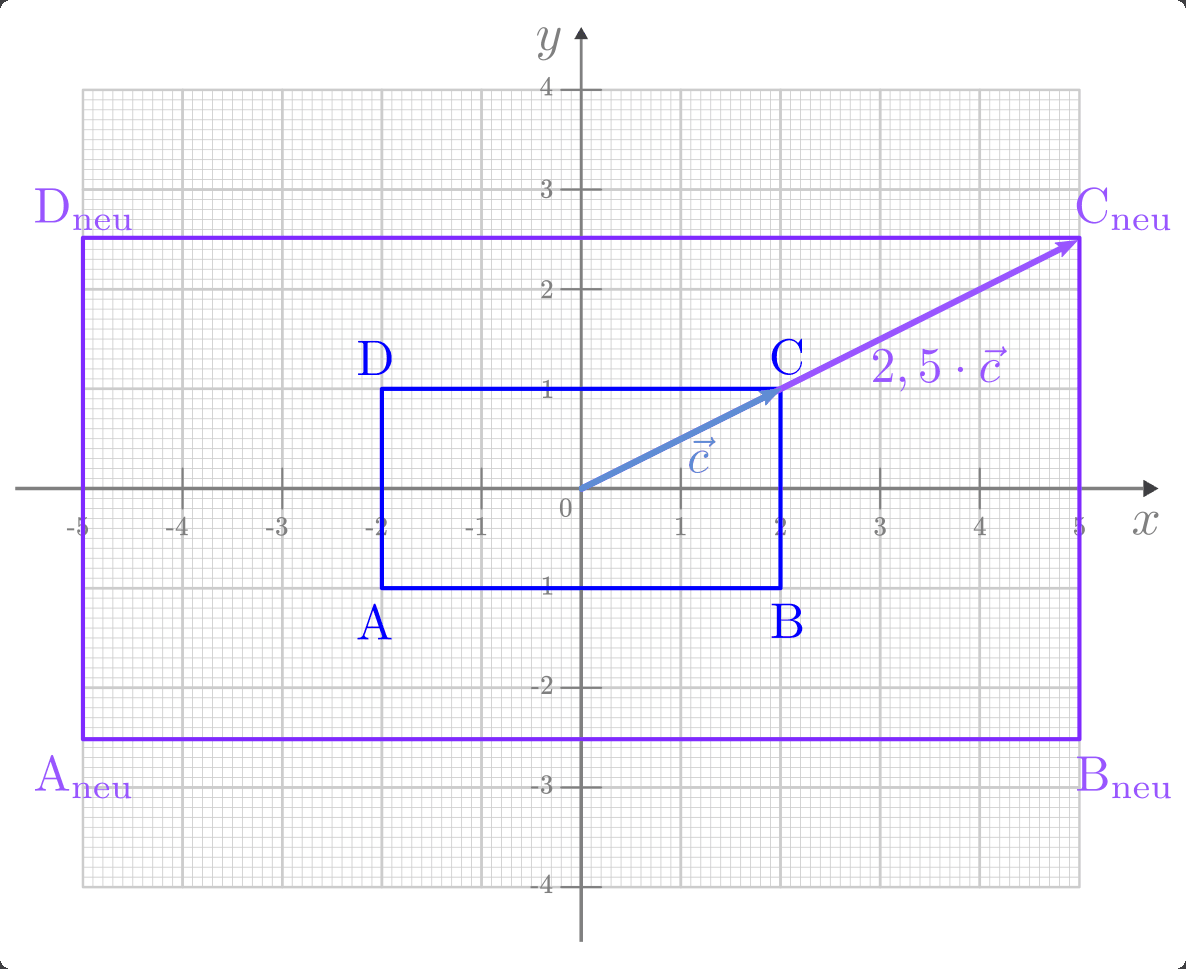
Man kann sich die Wirkungsweise der Matrix beispielhaft anhand des Ortsvektors
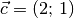 des Punktes
des Punktes  veranschaulichen:
veranschaulichen: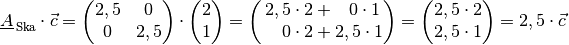
Die Koordinaten-Berechnung der übrigen neuen Punkte erfolgt nach dem gleichen Schema: Man erhält für jeden der Punkte einen Ortsvektor, der um einen Faktor
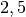 gestreckt ist.
gestreckt ist.
Gilt für die Skalierungsgröße 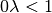 , so wird der Vektor
beziehungsweise ein aus vielerlei Vektoren bestehendes geometrisches Objekt
durch die Matrix originalgetreu verkleinert (gestaucht). Beispielsweise würde im
obigen Beispiel ein Skalierungsfaktor von
, so wird der Vektor
beziehungsweise ein aus vielerlei Vektoren bestehendes geometrisches Objekt
durch die Matrix originalgetreu verkleinert (gestaucht). Beispielsweise würde im
obigen Beispiel ein Skalierungsfaktor von 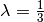 eine
Umkehrung der Skalierung mit dem Faktor
eine
Umkehrung der Skalierung mit dem Faktor  zur Folge haben.
zur Folge haben.
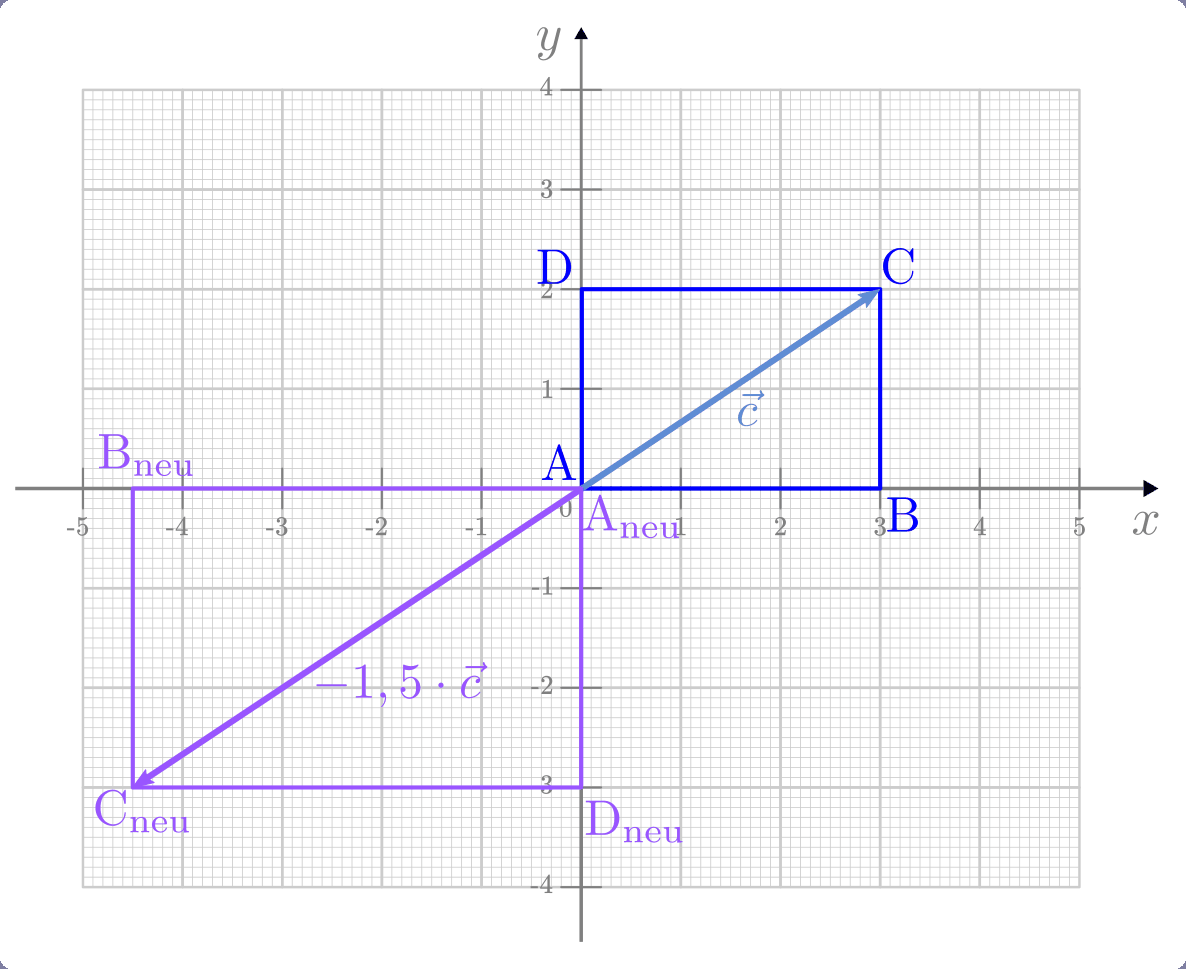
Gilt für die Skalierungsgröße 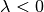 , so wird jeder Ortsvektor, auf
den die Matrix angewendet wird, nicht nur um den Faktor
, so wird jeder Ortsvektor, auf
den die Matrix angewendet wird, nicht nur um den Faktor 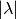 skaliert, sondern es wird zusätzlich sein Vorzeichen vertauscht. Hierdurch wird
die Richtung des Ortsvektors umgedreht: Beispielsweise zeigt ein Vektor, der
ursprünglich nach rechts oben gezeigt hat, nach einer Skalierung mit einem
negativen Skalierungsfaktor nach links unten. der Ortsvektor beziehungsweise das
geometrische Objekt erfährt dadurch eine zentrische Streckung am Koordinaten-Ursprung.
skaliert, sondern es wird zusätzlich sein Vorzeichen vertauscht. Hierdurch wird
die Richtung des Ortsvektors umgedreht: Beispielsweise zeigt ein Vektor, der
ursprünglich nach rechts oben gezeigt hat, nach einer Skalierung mit einem
negativen Skalierungsfaktor nach links unten. der Ortsvektor beziehungsweise das
geometrische Objekt erfährt dadurch eine zentrische Streckung am Koordinaten-Ursprung.
Beispiel:
Wird eine Skalierungsmatrix
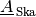 mit
mit
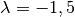 mit einem Ortsvektor multipliziert, so wird dieser um
den Faktor
mit einem Ortsvektor multipliziert, so wird dieser um
den Faktor 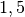 gestreckt und um
gestreckt und um ![\unit[180]{\degree}](../_images/math/a62139d45d177455d34d6e27e1030722257dea2f.png) um den
Koordinatenursprung gedreht. Dies soll am Beispiel eines Rechtecks gezeigt
werden, dessen Eckpunkte folgende Koordinaten haben:
um den
Koordinatenursprung gedreht. Dies soll am Beispiel eines Rechtecks gezeigt
werden, dessen Eckpunkte folgende Koordinaten haben: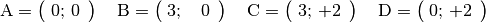
Man kann sich die Wirkungsweise der Matrix wiederum beispielhaft anhand des Ortsvektors
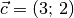 des Punktes
des Punktes  veranschaulichen:
veranschaulichen: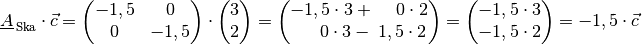
Die Koordinaten-Berechnung der übrigen neuen Punkte erfolgt wiederum nach dem gleichen Schema; man erhält somit ein um den Faktor
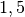 skaliertes
Objekt im gegenüber liegenden Quadranten.
skaliertes
Objekt im gegenüber liegenden Quadranten.
Spiegelungsmatrizen:
Soll ein (Orts-)Vektor an der  - oder an der
- oder an der  -Achse eines
zweidimensionalen Koordinatensystems gespiegelt werden, so ist dies mittels der
folgenden Matrizen möglich:
-Achse eines
zweidimensionalen Koordinatensystems gespiegelt werden, so ist dies mittels der
folgenden Matrizen möglich:
(12)¶![\text{Spiegelung an der $x$-Achse:} \quad \underline{A}_{\mathrm{\,Spi}} =
\begin{pmatrix}
\phantom{+}1 & \phantom{+}0 \;\phantom{.}\\
\phantom{+}0 & - 1 \;\phantom{.}
\end{pmatrix} \\[12pt]
\text{Spiegelung an der $y$-Achse:} \quad \underline{A}_{\mathrm{\,Spi}} =
\begin{pmatrix}
-1 & \phantom{+}0 \; \phantom{.}\\
\phantom{+}0 & \phantom{+}1 \;\phantom{.}
\end{pmatrix} \\[8pt]](../_images/math/e995fefb73785a4f925ed878009628472b9cc83b.png)
Diese beiden Spiegelungsmatrizen ähneln einer Skalierungsmatrix mit der
Skalierungsgröße 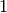 ; auch sie lassen die Länge eines Vektors
beziehungsweise die Größe eines durch mehrere (Orts-)Vektoren festgelegten
Objekts unverändert. Der Unterschied zur reinen Skalierung liegt also in dem nun
auftretenden Minus-Zeichen.
; auch sie lassen die Länge eines Vektors
beziehungsweise die Größe eines durch mehrere (Orts-)Vektoren festgelegten
Objekts unverändert. Der Unterschied zur reinen Skalierung liegt also in dem nun
auftretenden Minus-Zeichen.
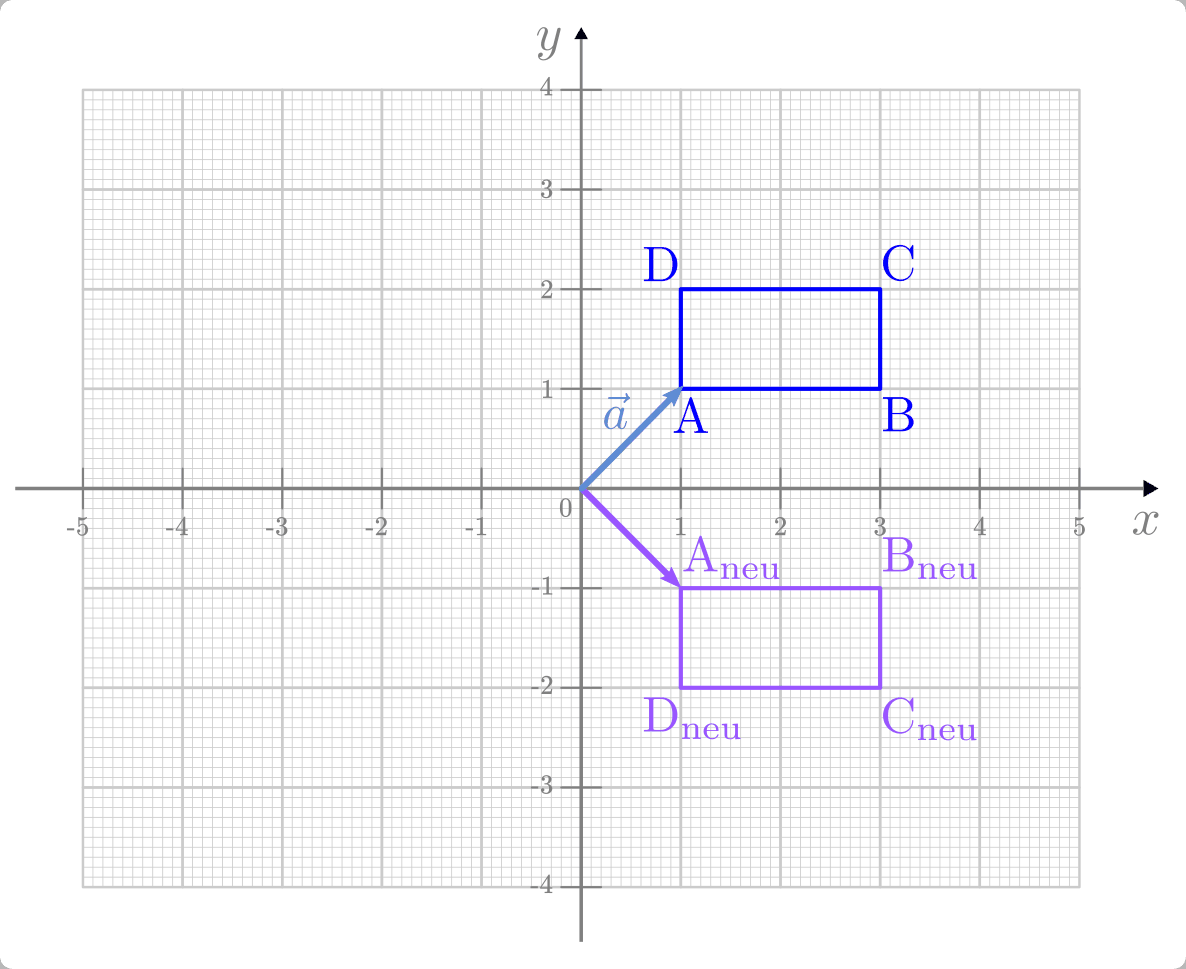
Beispiel:
Das Rechteck mit den folgenden Eckpunkten soll an der
 -Achse
gespiegelt werden:
-Achse
gespiegelt werden:
Wendet man die obige Spiegelungsmatrix beispielsweise auf den Ortsvektor
 des Punktes
des Punktes 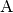 an, so erhält man:
an, so erhält man: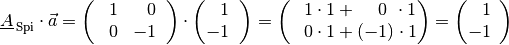
Die Matrix lässt also die
 -Komponente des Vektors, mit dem sie
multipliziert wird, unverändert; die
-Komponente des Vektors, mit dem sie
multipliziert wird, unverändert; die  -Komponente des Vektors hingegen
erhält ein umgekehrtes Vorzeichen.
-Komponente des Vektors hingegen
erhält ein umgekehrtes Vorzeichen.
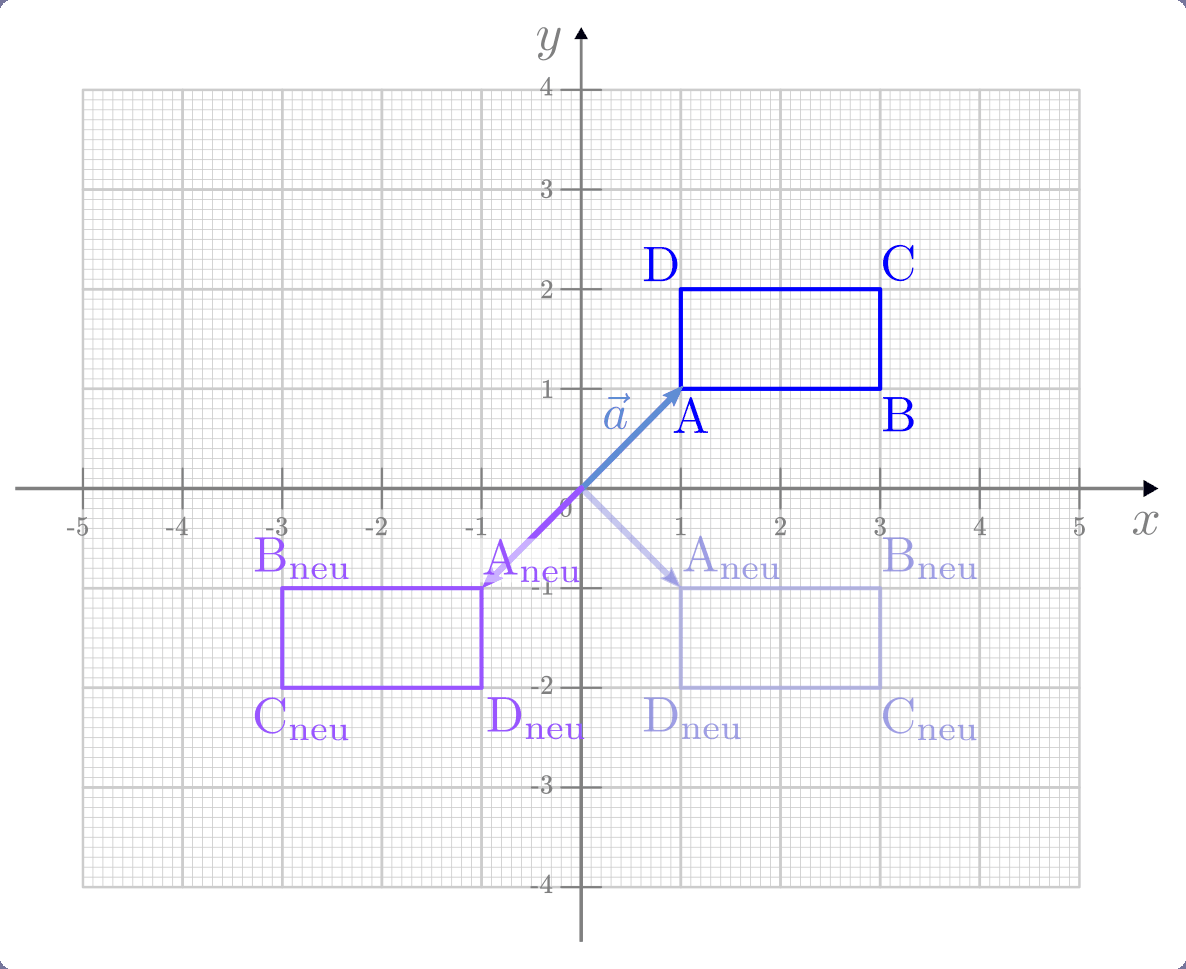
Die Spiegelung an der  -Achse erfolgt nach dem gleichen Prinzip; die
entsprechende Matrix lässt hierbei allerdings die
-Achse erfolgt nach dem gleichen Prinzip; die
entsprechende Matrix lässt hierbei allerdings die  -Komponente des
Vektors unverändert, während die
-Komponente des
Vektors unverändert, während die  -Komponente ein umgekehrtes Vorzeichen
erhält.
-Komponente ein umgekehrtes Vorzeichen
erhält.
Wendet man die gleiche Spiegelungsmatrix zweimal hintereinander auf einen Vektor
beziehungsweise ein geometrisches Objekt an, so stimmt das Resultat mit dem
ursprünglichen Objekt überein. Nimmt man hingegen zuerst eine Spiegelung an der
 - und anschließend eine Spiegelung an der
- und anschließend eine Spiegelung an der  -Achse vor, so
erhält man eine Punktspiegelung des ursprünglichen
Objekts um den Koordinatenursprung.
-Achse vor, so
erhält man eine Punktspiegelung des ursprünglichen
Objekts um den Koordinatenursprung.
Eine Punktspiegelung ist formal mit einer Skalierung des Objekts mit dem Faktor
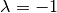 identisch. Dies lässt sich unter anderem mittels des
Assoziativ-Gesetzes der Matrix-Multiplikation zeigen:
identisch. Dies lässt sich unter anderem mittels des
Assoziativ-Gesetzes der Matrix-Multiplikation zeigen:
![\underline{A}_{\mathrm{\,Spi,y}} \cdot
\left(\underline{A}_{\mathrm{\,Spi,x}} \cdot \vec{a}\right) &=
\left(\underline{A}_{\mathrm{\,Spi,y}} \cdot \underline{A}_{\mathrm{\,Spi,x}}\right) \cdot \vec{a} \\[4pt]
&= \underbrace{\left[\begin{pmatrix}
\phantom{-}1 & \phantom{+}0 \,\phantom{.} \\
\phantom{+}0 & -1\,\phantom{.}
\end{pmatrix} \cdot \begin{pmatrix}
-1 & \phantom{+}0 \,\phantom{.} \\
\phantom{+}0 & \phantom{-}1\,\phantom{.}
\end{pmatrix} \right]}_{} \cdot \vec{a} \\[4pt]
&= \qquad \quad \;\, \begin{pmatrix}
-1 & \phantom{+}0 \,\phantom{.} \\
\phantom{+}0 & -1 \,\phantom{.} \\
\end{pmatrix} \qquad \quad \;\, \cdot \vec{a} \qquad \checkmark](../_images/math/0133ce128f30904413e74a3bb35d088bcf69481e.png)
Projektionsmatrizen
Mittels einer Projektionsmatrix lässt sich ein Vektor, wie der Name schon
sagt, auf die  - beziehungsweise
- beziehungsweise  -Achse „projezieren“.
Anschaulich kann man sich eine solche Projektion als „Schatten“ des Vektors
vorstellen, der sich bei einer Beleuchtung des Vektors senkrecht zur jeweiligen
Achse ergeben würde.
Um einen (Orts-)Vektor auf die
-Achse „projezieren“.
Anschaulich kann man sich eine solche Projektion als „Schatten“ des Vektors
vorstellen, der sich bei einer Beleuchtung des Vektors senkrecht zur jeweiligen
Achse ergeben würde.
Um einen (Orts-)Vektor auf die  - beziehungsweise
- beziehungsweise  -Achse
abzubilden, kann jeweils folgende Matrix genutzt werden:
-Achse
abzubilden, kann jeweils folgende Matrix genutzt werden:
(13)¶![\text{Projektion auf die $x$-Achse:} \quad \underline{A}_{\mathrm{\,Pro}} = \begin{pmatrix}
\phantom{+} 1 & \phantom{+}0 \;\phantom{.} \\
\phantom{+} 0 & \phantom{+}0 \;\phantom{.} \\
\end{pmatrix} \\[12pt]
\text{Projektion auf die $y$-Achse:} \quad \underline{A}_{\mathrm{\,Pro}} = \begin{pmatrix}
\phantom{+} 0 & \phantom{+}0 \;\phantom{.} \\
\phantom{+} 0 & \phantom{+}1 \;\phantom{.} \\
\end{pmatrix}](../_images/math/aebabcdf642840973299abfb65e65aeff6e7e52e.png)
Beispiel:
Der Vektor
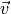 , der die Punkte
, der die Punkte 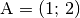 und
und
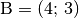 miteinander verbindet, soll auf die
miteinander verbindet, soll auf die
 -Achse projeziert werden.
-Achse projeziert werden.Für die senkrechten Projektionen der Punkte
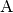 und
und
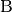 ergibt sich durch Anwenden der entsprechenden
Projektionsmatrix auf die zugehörigen Ortsvektoren:
ergibt sich durch Anwenden der entsprechenden
Projektionsmatrix auf die zugehörigen Ortsvektoren:![\mathrm{A_x} = \underline{A}_{\mathrm{\,Pro}} \cdot \overrightarrow{\mathrm{0A}} =
\begin{pmatrix}
\,\phantom{.} 1 & 0 \,\phantom{.} \\
\,\phantom{.} 0 & 0 \,\phantom{.} \\
\end{pmatrix} \cdot \begin{pmatrix}
\,\phantom{.} 1 \,\phantom{.} \\
\,\phantom{.} 2 \,\phantom{.} \\
\end{pmatrix} = \begin{pmatrix}
1 \\ 0
\end{pmatrix} \\[12pt]
\mathrm{B_x} = \underline{A}_{\mathrm{\,Pro}} \cdot \overrightarrow{\mathrm{0B}} =
\begin{pmatrix}
\,\phantom{.} 1 & 0 \,\phantom{.} \\
\,\phantom{.} 0 & 0 \,\phantom{.} \\
\end{pmatrix} \cdot \begin{pmatrix}
\,\phantom{.} 4 \,\phantom{.} \\
\,\phantom{.} 3 \,\phantom{.} \\
\end{pmatrix} = \begin{pmatrix}
4 \\ 0
\end{pmatrix}](../_images/math/414e44040afac8b51505a7b3f5650e69b0a3e0f3.png)
Den projezierten Vektor
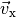 zum Vektor
zum Vektor 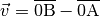 erhält man entweder, indem
man die Differenz der Ortsvektoren von
erhält man entweder, indem
man die Differenz der Ortsvektoren von 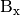 und
und
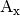 bildet, oder auch indem man die entsprechende
Projektionsmatrix auf den Vektor
bildet, oder auch indem man die entsprechende
Projektionsmatrix auf den Vektor 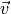 anwendet:
anwendet:![\underline{A}_{\mathrm{\,Pro}} \cdot \vec{v} = \begin{pmatrix}
\,\phantom{.} 1 & 0 \,\phantom{.} \\
\,\phantom{.} 0 & 0 \,\phantom{.} \\
\end{pmatrix} \cdot \left[ \begin{pmatrix}
\,\phantom{.} 4 \,\phantom{.} \\
\,\phantom{.} 3 \,\phantom{.} \\
\end{pmatrix} - \begin{pmatrix}
\,\phantom{.} 1 \,\phantom{.} \\
\,\phantom{.} 2 \,\phantom{.} \\
\end{pmatrix} \right] = \begin{pmatrix}
\,\phantom{.} 1 & 0 \,\phantom{.} \\
\,\phantom{.} 0 & 0 \,\phantom{.} \\
\end{pmatrix} \cdot \begin{pmatrix}
\,\phantom{.} 3 \,\phantom{.} \\
\,\phantom{.} 1 \,\phantom{.} \\
\end{pmatrix} = \begin{pmatrix}
3 \\ 0
\end{pmatrix}](../_images/math/99f7bde64cec6b6c6be184cbdcc9ef518ca1e38c.png)
Der „Schatten“ des Vektor
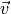 lässt sich somit rechnerisch mittels
des Ausdrucks
lässt sich somit rechnerisch mittels
des Ausdrucks 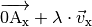 mit
mit 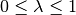 beschreiben.[2]
beschreiben.[2]
Drehmatrizen
Soll ein Vektor um einen Winkel 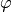 in positiver Winkelrichtung
(also gegen den Uhrzeigersinn) um den Koordinatenursprung gedreht werden, so ist
dies mittels der folgenden Drehmatrix möglich:
in positiver Winkelrichtung
(also gegen den Uhrzeigersinn) um den Koordinatenursprung gedreht werden, so ist
dies mittels der folgenden Drehmatrix möglich:
(14)¶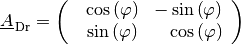
Die Wirkungsweise dieser Matrix kann man sich gut anhand einiger Sonderfälle veranschaulichen:
Ist der Drehwinkel
![\varphi = \unit[0]{\degree}](../_images/math/ca9abafecc5d9999dc998e8d40eb72a251e94852.png) , so ist
, so ist
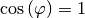 und
und 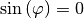 . Die Drehmatrix nimmt in diesem Fall folgende Form an:
. Die Drehmatrix nimmt in diesem Fall folgende Form an:![\underline{A}_{\mathrm{\,Dr,\varphi=\unit[0]{\!\degree}}} = \begin{pmatrix}
\phantom{+}1 & \phantom{+}0 \,\phantom{.}
\\ \phantom{+}0 & \phantom{+}1 \,\phantom{.}
\end{pmatrix}](../_images/math/532df7e3e4c4c04ea9eec9490e7ec750e337890b.png)
Diese Matrix entspricht der Einheits-Matrix, die jeden Vektor unverändert lässt; eine Drehung um
![\unit[0]{\degree}](../_images/math/c3fc7de542fb1aa97f77e9c8d4ba7091326bea84.png) hat somit keine Auswirkung
auf geometrische Objekte.
hat somit keine Auswirkung
auf geometrische Objekte.Ist der Drehwinkel
![\varphi = \unit[180]{\degree}](../_images/math/9c78f5e09e2596aa6b96f48c214cfa7108c29da6.png) , so ist
, so ist
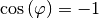 und
und 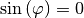 . Die Drehmatrix nimmt in diesem Fall folgende Form an:
. Die Drehmatrix nimmt in diesem Fall folgende Form an:![\underline{A}_{\mathrm{\,Dr,\varphi=\unit[0]{\!\degree}}} = \begin{pmatrix}
-1 & \phantom{+}0 \,\phantom{.}\\ \phantom{+}0 & -1\,\phantom{.}
\end{pmatrix}](../_images/math/7169bbd0feee049d1e0b40ca6f1301fed5e3e055.png)
Diese Matrix entspricht einer Skalierungsmatrix mit dem Faktor
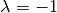 ; diese bewirkt, wie bereits beschrieben, eine Punktspiegelung eines
geometrischen Objekts um den Koordinaten-Ursprung und somit eine Drehung um
; diese bewirkt, wie bereits beschrieben, eine Punktspiegelung eines
geometrischen Objekts um den Koordinaten-Ursprung und somit eine Drehung um
![\unit[180]{\degree}](../_images/math/a62139d45d177455d34d6e27e1030722257dea2f.png) .
.Ist der Drehwinkel
![\varphi = \unit[45]{\degree}](../_images/math/52b16c846a2e2fcb270420742fed93303c517408.png) , so ist
, so ist
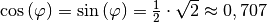 . Die Drehmatrix nimmt in diesem Fall folgende
Form an:
. Die Drehmatrix nimmt in diesem Fall folgende
Form an:![\underline{A}_{\mathrm{\,Dr,\varphi=\unit[45]{\!\degree}}} =
\frac{\sqrt{2}}{2} \cdot \begin{pmatrix}
\phantom{-}1 & -1 \,\phantom{.} \\ \phantom{-}1 & \phantom{-}1 \,\phantom{.}
\end{pmatrix}](../_images/math/438abc4e7d510886aef798069d6b903154e72aaa.png)
Der Faktor
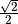 , der in diesem Fall bei allen
Komponenten der Matrix auftritt, bewirkt eine Skalierung des geometrischen
Objekts; ansonsten besteht der Unterschied zu den bisherigen Matrizen darin,
dass nun alle Elemente der Matrix von Null verschieden sind.
, der in diesem Fall bei allen
Komponenten der Matrix auftritt, bewirkt eine Skalierung des geometrischen
Objekts; ansonsten besteht der Unterschied zu den bisherigen Matrizen darin,
dass nun alle Elemente der Matrix von Null verschieden sind.Die Wirkungsweise der obigen Matrix soll anhand einer Drehung der beiden Punkte
 und
und 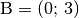 beziehungsweise der zugehörigen Ortsvektoren
beziehungsweise der zugehörigen Ortsvektoren  und
und
 um
um ![\varphi = \unit[45]{\degree}](../_images/math/52b16c846a2e2fcb270420742fed93303c517408.png) veranschaulicht
werden. Man erhält in diesem Fall für die Koordinaten des neuen Punktes
veranschaulicht
werden. Man erhält in diesem Fall für die Koordinaten des neuen Punktes
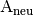 :
:![\underline{A}_{\mathrm{\,Dr,\varphi=\unit[45]{\!\degree}}} \cdot \vec{a} =
\frac{\sqrt{2}}{2} \cdot \begin{pmatrix}
\phantom{+}1 & -1 \,\phantom{.} \\ \phantom{+}1 & \phantom{-}1 \,\phantom{.}
\end{pmatrix} \cdot \begin{pmatrix}
3 \\ 0
\end{pmatrix} = \frac{\sqrt{2}}{2} \cdot \begin{pmatrix}
\phantom{-}3 \\ \phantom{-}3
\end{pmatrix} \\[12pt]
\underline{A}_{\mathrm{\,Dr,\varphi=\unit[45]{\!\degree}}} \cdot \vec{b} =
\frac{\sqrt{2}}{2} \cdot \begin{pmatrix}
\phantom{+}1 & -1 \,\phantom{.} \\ \phantom{+}1 & \phantom{-}1 \,\phantom{.}
\end{pmatrix} \cdot \begin{pmatrix}
0 \\ 3
\end{pmatrix} = \frac{\sqrt{2}}{2} \cdot \begin{pmatrix}
-3 \\ \phantom{-}3
\end{pmatrix} \\[12pt]](../_images/math/0fd1eea8983db571ba6ed1fe4735e29fc1d1b12d.png) Die neuen Punkte haben somit gerundet die Koordinaten
Die neuen Punkte haben somit gerundet die Koordinaten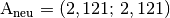 und
und
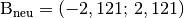 .Berechnet man die Länge der neuen Ortsvektoren, so stellt man fest, dass sich diese durch die Anwendung der Drehmatrix nicht geändert haben:
.Berechnet man die Länge der neuen Ortsvektoren, so stellt man fest, dass sich diese durch die Anwendung der Drehmatrix nicht geändert haben:![\left| \vec{a}_{\mathrm{neu}} \right| = \sqrt{\left( \frac{3\cdot \sqrt{2}}{2}
\right)^2 + \left(\phantom{-} \frac{3\cdot \sqrt{2}}{2} \right)^2 } = \sqrt{\frac{9\cdot 2}{4} +
\frac{9\cdot 2}{4}} = \sqrt{9} = 3 \quad \checkmark \\[4pt]
\left| \vec{b}_{\mathrm{neu}} \right| = \sqrt{\left( \frac{3\cdot \sqrt{2}}{2}
\right)^2 + \left(- \frac{3\cdot \sqrt{2}}{2} \right)^2 } = \sqrt{\frac{9 \cdot 2}{4} +
\frac{9\cdot 2}{4}} = \sqrt{9} = 3 \quad \checkmark \\[4pt]](../_images/math/dbe9cad1ae897d0e162bac5dda79df214ead66c8.png)
Drehmatrizen bilden geometrische Objekte also längentreu ab. zudem bleibt auch der Winkel zwischen den beiden Ortsvektoren identisch, wie man durch Bildung des Skalarprodukts der beiden neuen Vektoren zeigen kann:
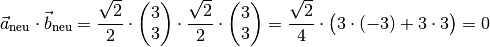
Da die Ortsvektoren einen von Null verschiedenen Betrag haben und für das Skalarprodukt
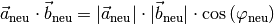 gilt, muss in diesem Fall
gilt, muss in diesem Fall
 sein, damit die rechte
Seite der Gleichung ebenfalls den Wert Null liefert; folglich ist auch der
Winkel
sein, damit die rechte
Seite der Gleichung ebenfalls den Wert Null liefert; folglich ist auch der
Winkel  zwischen den neuen Vektoren gleich
zwischen den neuen Vektoren gleich
![\unit[90]{\degree}](../_images/math/ed42da9b82869c64cf4a98987530ceace4d59e0e.png) .
.
Bei Drehungen um beliebige Winkel erhält man für die neuen Ortsvektoren meist Werte, die sich nur auf einige Nachkomma-Stellen gerundet angeben lassen; allerdings lässt sich bereits bei vier Nachkomma-Stellen eine für die meisten Zwecke ausreichende Genauigkeit erzielen. In jedem Fall bleiben die gedrehten Objekte längen- und winkeltreu.[3]
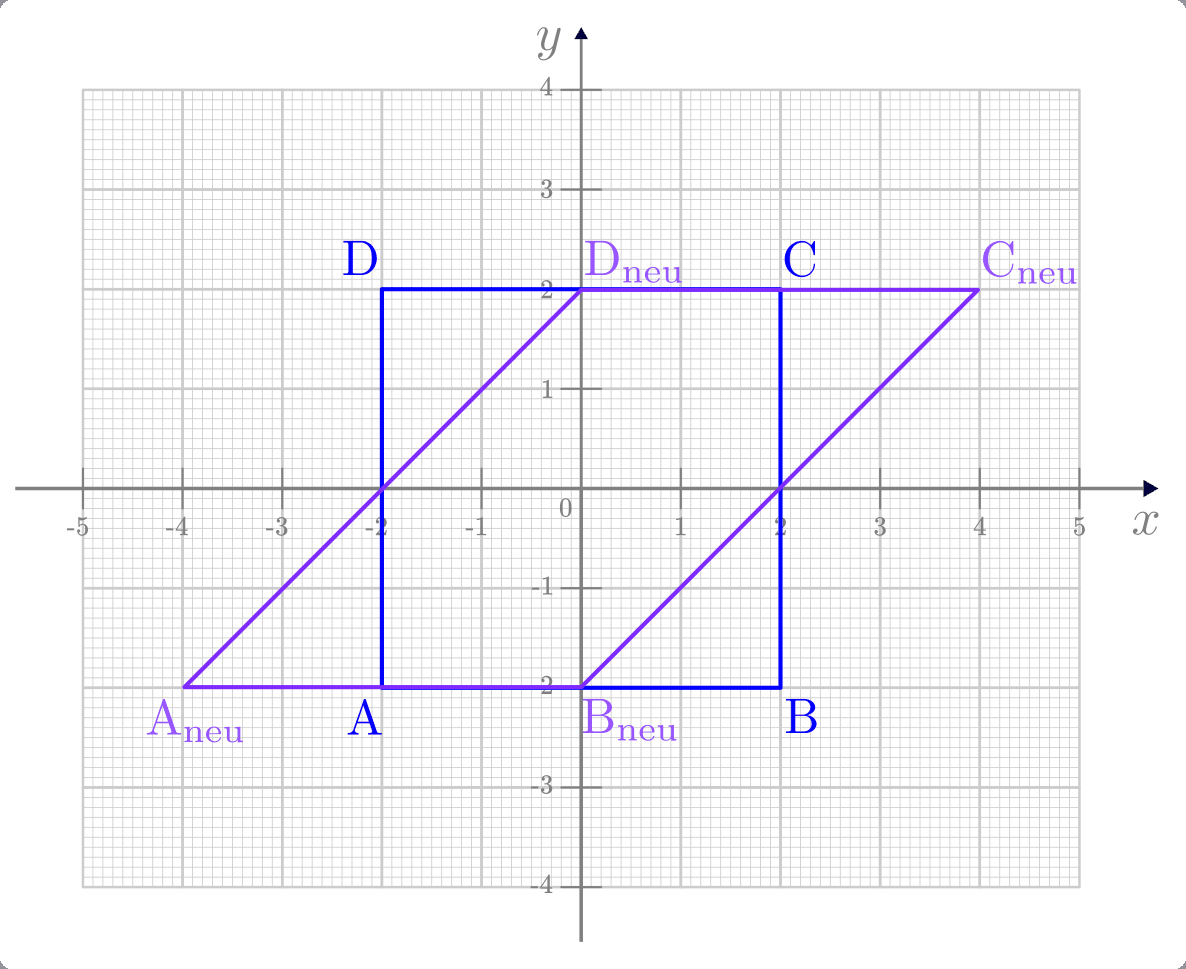
Scherungsmatrizen
Eine Scherungsmatrix bewirkt eine Verformung eines geometrischen Objekts. Allgemein hat eine zweidimensionale Scherungsmatrix folgende Form:
(15)¶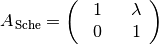
Die Wirkungsweise einer Scherungsmatrix soll im folgenden anhand des Beispiels
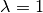 verdeutlicht werden.
verdeutlicht werden.
Beispiel:
Wie verändert eine Scherungsmatrix mit
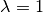 ein Quadrat, das
durch folgende Punkte begrenzt wird?
ein Quadrat, das
durch folgende Punkte begrenzt wird?
Um die Punkte des neuen Vierecks zu erhalten, kann man die Scherungsmatrix auf die Ortsvektoren der einzelnen Eckpunkte anwenden:
![A_{\mathrm{\,Sche}} \cdot \vec{a} &= \begin{pmatrix}
\phantom{+} 1 & \phantom{+}1 \,\phantom{.} \\
\phantom{+} 0 & \phantom{+}1 \,\phantom{.} \\
\end{pmatrix} \cdot \begin{pmatrix}
-2 \,\phantom{.}\\ -2 \,\phantom{.}
\end{pmatrix} = \begin{pmatrix}
-2 - 2 \\ \phantom{+}0-2
\end{pmatrix} = \begin{pmatrix}
-4 \\ -2
\end{pmatrix} \\[4pt]
A_{\mathrm{\,Sche}} \cdot \vec{b} &= \begin{pmatrix}
\phantom{+} 1 & \phantom{+}1 \,\phantom{.} \\
\phantom{+} 0 & \phantom{+}1 \,\phantom{.} \\
\end{pmatrix} \cdot \begin{pmatrix}
\phantom{+}2 \,\phantom{.}\\ -2 \,\phantom{.}
\end{pmatrix} = \begin{pmatrix}
\phantom{+}2 - 2 \\ \phantom{+}0-2
\end{pmatrix} = \begin{pmatrix}
\phantom{+}0 \\ -2
\end{pmatrix} \\[4pt]
A_{\mathrm{\,Sche}} \cdot \vec{c} &= \begin{pmatrix}
\phantom{+} 1 & \phantom{+}1 \,\phantom{.} \\
\phantom{+} 0 & \phantom{+}1 \,\phantom{.} \\
\end{pmatrix} \cdot \begin{pmatrix}
\phantom{+}2 \,\phantom{.}\\ \phantom{+}2 \,\phantom{.}
\end{pmatrix} = \begin{pmatrix}
\phantom{+}2 + 2 \\ \phantom{+}0+2
\end{pmatrix} = \begin{pmatrix}
\phantom{+}4 \\ \phantom{+}2
\end{pmatrix} \\[4pt]
A_{\mathrm{\,Sche}} \cdot \vec{d} &= \begin{pmatrix}
\phantom{+} 1 & \phantom{+}1 \,\phantom{.} \\
\phantom{+} 0 & \phantom{+}1 \,\phantom{.} \\
\end{pmatrix} \cdot \begin{pmatrix}
-2 \,\phantom{.}\\ \phantom{+}2 \,\phantom{.}
\end{pmatrix} = \begin{pmatrix}
-2 + 2 \\ \phantom{+}0+2
\end{pmatrix} = \begin{pmatrix}
\phantom{+}0 \\ \phantom{+}2
\end{pmatrix} \\[4pt]](../_images/math/dde994470071f378f42a0503de691fd460a1cc36.png)
Durch die Anwendung der Scherungsmatrix wird ein geometrisches Objekt also „verzerrt“. Der Flächeninhalt des Objekts, im obigen Beispiel eines Quadrats, bleibt bei der Scherung zwar gleich, jedoch ändern sich die Winkel zwischen den einzelnen Seiten.
Matrizengleichungen¶
Matrizen können auch zur Lösung von linearen Gleichungssystemen genutzt werden. Bei Verwendung von Matrizen können diese sehr kompakt dargestellt werden. Beispielsweise hat ein lineares Gleichungssystem mit drei Unbekannten folgende Form:

In Matrizenschreibweise kann dies folgendermaßen geschrieben werden:
(16)¶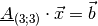
Gesucht sind bei dieser „Matrizengleichung“ wiederum die Komponenten
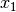 ,
, 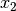 und
und 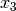 des Vektors
des Vektors  . Man kann
allerdings, um die Gleichung zu lösen, nicht einfach durch
. Man kann
allerdings, um die Gleichung zu lösen, nicht einfach durch 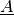 dividieren, da die Division durch eine Matrix nicht definiert ist. Die Lösung
besteht vielmehr darin, eine so genannte „inverse“ Matrix
dividieren, da die Division durch eine Matrix nicht definiert ist. Die Lösung
besteht vielmehr darin, eine so genannte „inverse“ Matrix 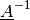 zu finden, die bei Multiplikation mit der Matrix
zu finden, die bei Multiplikation mit der Matrix 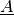 eine Einheitsmatrix ergibt.[4]
eine Einheitsmatrix ergibt.[4]
(17)¶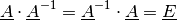
Hat man eine solche inverse Matrix  zur Matrix
zur Matrix
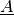 gefunden, kann man beide Seiten der obigen Gleichung
(16) damit multiplizieren:
gefunden, kann man beide Seiten der obigen Gleichung
(16) damit multiplizieren:
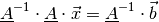
Mit 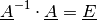 folgt damit:
folgt damit:
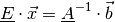
Da die Einheitsmatrix das neutrale Element bezüglich der Multiplikation ist,
also  gilt, folgt somit als Lösung
für
gilt, folgt somit als Lösung
für  :
:
(18)¶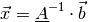
Die eigentliche Aufgabe für die Lösung einer Matrizengleichung besteht nun also
darin, zu einer Matrix 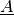 die inverse Matrix
die inverse Matrix
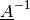 zu finden. Hierzu muss folgende Gleichung gelöst
werden:
zu finden. Hierzu muss folgende Gleichung gelöst
werden:

Alle  mit
mit 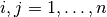 sind
Unbekannte; es muss also ein Gleichungssystem mit
sind
Unbekannte; es muss also ein Gleichungssystem mit 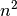 Unbekannten und
Unbekannten und
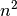 Gleichungen zur Bestimmung der inversen Matrix gelöst werden.
Gleichungen zur Bestimmung der inversen Matrix gelöst werden.
… to be continued …
Anmerkungen:
| [1] | Bisweilen werden beim Falk-Schema, um eine einfachere Textsatzung zu ermöglichen, entweder die Klammern der Matrizen oder die beiden zueinander senkrechten Tabellenlinien weggelassen. |
| [2] | Ist der Zahlenwert der Projektionsmatrix ungleich Eins, so wird der Schatten skaliert und die Projektion entsprechend schräg. Soll ein dreidimensionaler Vektor auf eine Ebene projeziert werden, so kann
dies ebenfalls mittels einer Projektionsmatrix erfolgen. Um beispielsweise
einen Vektor
|
| [3] | Soll die Drehung in die entgegengesetzte Richtung, also mit dem Uhrzeigersinn erfolgen, so muss das Minus-Zeichen vor die andere Sinus-Komponente der Drehmatrix gesetzt werden:
|
| [4] | Die Schreibweise 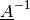 soll auf die Ähnlichkeit zur
Schreibweise soll auf die Ähnlichkeit zur
Schreibweise 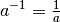 für reelle Zahlen hinweisen, für
die ebenfalls für reelle Zahlen hinweisen, für
die ebenfalls 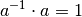 gilt. Es kann allerdings nicht gilt. Es kann allerdings nicht
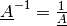 sein, da eine Division
durch eine Matrix nicht definiert ist. sein, da eine Division
durch eine Matrix nicht definiert ist. |



 -Ebene zu projezieren, kann
folgende Matrix auf den Vektor angewendet werden:
-Ebene zu projezieren, kann
folgende Matrix auf den Vektor angewendet werden: