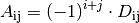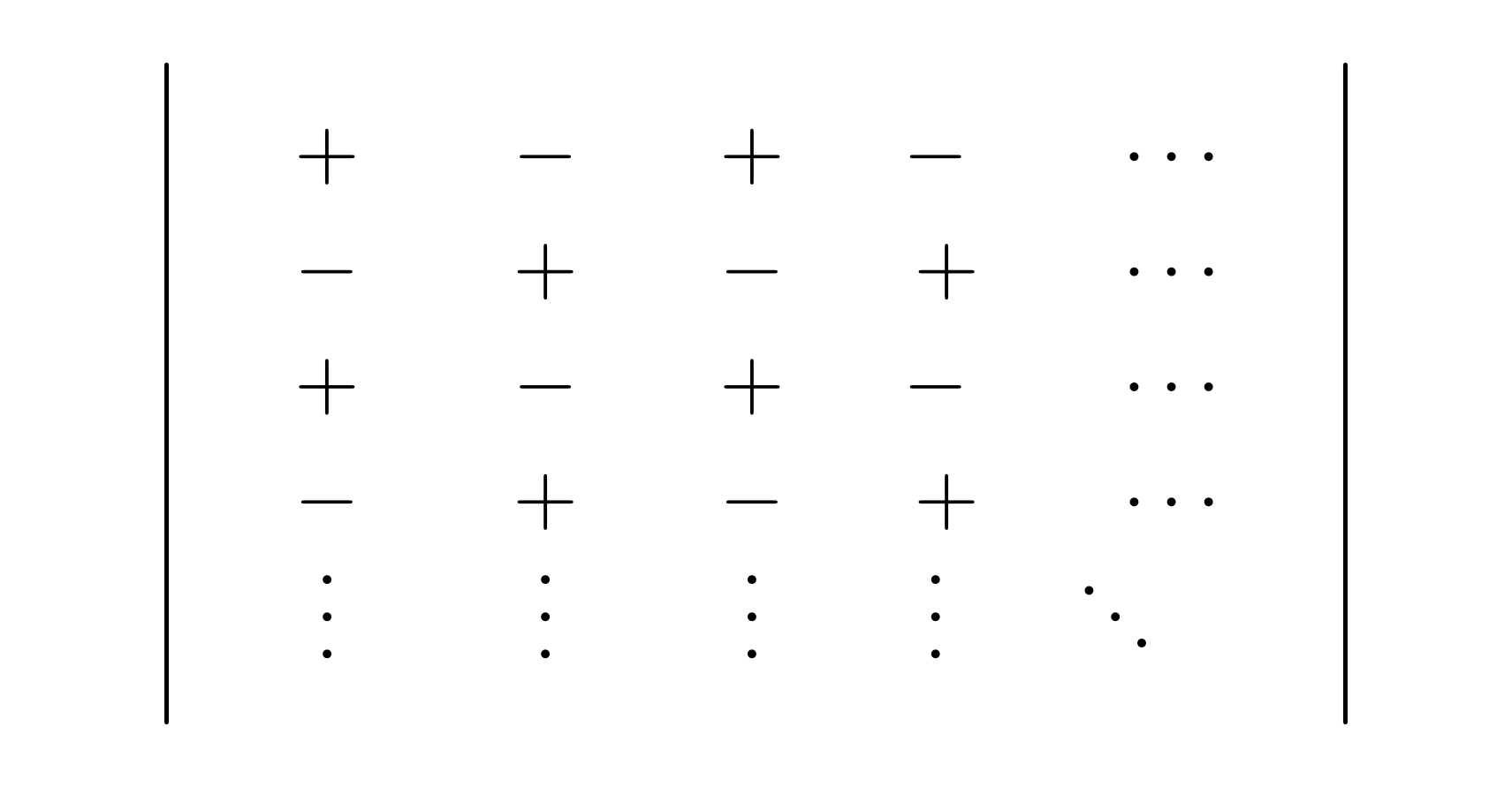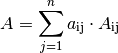Determinanten¶
Determinanten stellen neben dem Gaussschen Lösungsverfahren ein weiteres nützliches Werkzeug im Umgang mit linearen Gleichungssystemen dar. Sie ermöglichen unter anderem eine verhältnismäßig einfache und schnelle Untersuchung, ob ein lineares Gleichungssystem eine eindeutige Lösung besitzt oder nicht.
Zweireihige Determinanten
Um den Umgang mit Determinanten zu verdeutlichen, werden im folgenden Abschnitt zunächst wiederum lineare Gleichungssysteme mit zwei Gleichungen und zwei Unbekannten betrachtet. Diese lassen sich im Allgemeinen in folgender Form darstellen:
Allgemein kann ein solches Gleichungssystem gelöst werden, indem man
beispielsweise die erste Gleichung mit 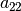 und die zweite Gleichung
mit
und die zweite Gleichung
mit 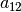 multipliziert. Es folgt:
multipliziert. Es folgt:
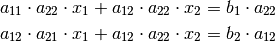
In dieser Form sind die Koeffizienten von 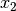 in beiden Gleichungen
identisch. Subtrahiert man die zweite Gleichung von der ersten, so erhält man
eine einzelne Gleichung für
in beiden Gleichungen
identisch. Subtrahiert man die zweite Gleichung von der ersten, so erhält man
eine einzelne Gleichung für 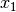 :
:
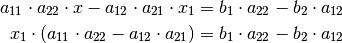
Im zweiten Rechenschritt wurde auf der linken Seite  ausgeklammert. Ist
die verbleibende Klammer ungleich Null, so erhält man als Lösung für
ausgeklammert. Ist
die verbleibende Klammer ungleich Null, so erhält man als Lösung für
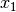 :
:

Nach dem gleichen Prinzip kann man im die erste Gleichung des ursprünglichen
Gleichungssystems mit 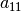 und die zweite Gleichung mit
und die zweite Gleichung mit
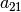 multiplizieren, um eine Bestimmungsgleichung für
multiplizieren, um eine Bestimmungsgleichung für
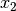 zu erhalten. Die Lösung lautet dabei:
zu erhalten. Die Lösung lautet dabei:
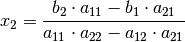
Die Lösbarkeit des Gleichungssystems hängt also nur davon ab, ob für den Term
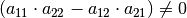 gilt. Die „Determinante“ eines Gleichungssystems wird daher folgendermaßen
definiert:
gilt. Die „Determinante“ eines Gleichungssystems wird daher folgendermaßen
definiert:
(1)¶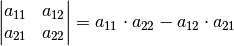
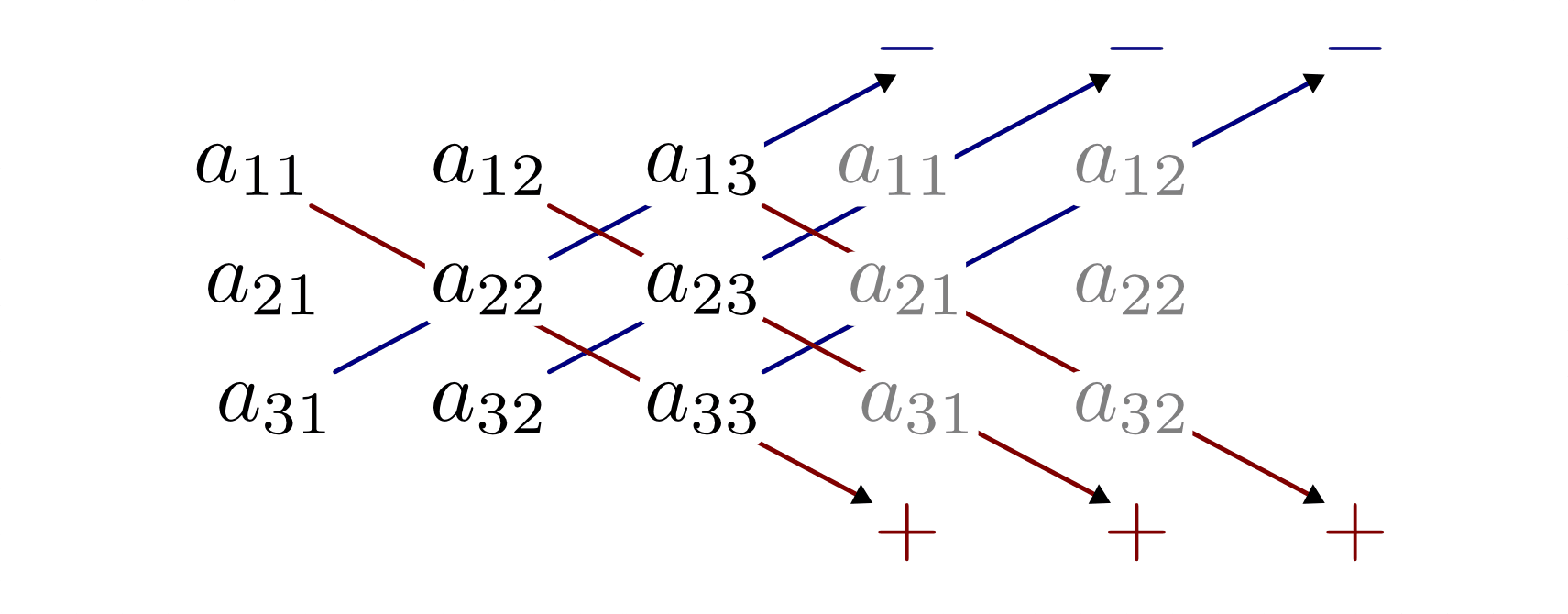
Das Ergebnis dieser Determinante lässt sich nach der so genannten „Regel von Sarrus“ berechnen, indem man das Produkt der in der „Hauptdiagonale“ stehenden Zahlen (von links oben nach rechts unten) bildet und davon das Produkt der in der „Nebendiagonalen“ stehenden Zahlen (von links unten nach rechts oben) subtrahiert. Ist die resultierende Zahl ungleich Null, so ist das Gleichungssystem eindeutig lösbar.
Die Lösungen für 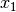 und
und 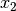 lassen sich nach der so genannten
Regel von Cramer ebenfalls in
Determinanten-Schreibweise darstellen. Im Nenner steht dabei immer die
eigentliche Determinante des Gleichungssystems, im Zähler wird die erste
beziehungsweise zweite Spalte der Determinante durch die rechte Seite der
Gleichung ersetzt. Somit gilt:
lassen sich nach der so genannten
Regel von Cramer ebenfalls in
Determinanten-Schreibweise darstellen. Im Nenner steht dabei immer die
eigentliche Determinante des Gleichungssystems, im Zähler wird die erste
beziehungsweise zweite Spalte der Determinante durch die rechte Seite der
Gleichung ersetzt. Somit gilt:
(2)¶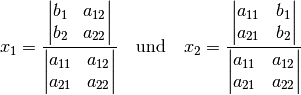
Dreireihige Determinanten
Determinanten lassen sich auch für Gleichungssysteme mit drei Gleichungen und drei Unbekannten definieren. In allgemeiner Form lässt sich ein solches Gleichungssystem folgendermaßen beschreiben:
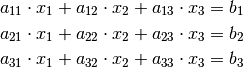
Entsprechend lässt sich hierfür eine Determinante in folgender Form definieren:
(3)¶![\begin{vmatrix}
a_{\mathrm{11}} & a_{\mathrm{12}} & a_{\mathrm{13}} \\
a_{\mathrm{21}} & a_{\mathrm{22}} & a_{\mathrm{23}} \\
a_{\mathrm{31}} & a_{\mathrm{32}} & a_{\mathrm{33}} \\
\end{vmatrix} &= \phantom{+}
a_{\mathrm{11}} \cdot a_{\mathrm{22}} \cdot a_{\mathrm{33}} +
a_{\mathrm{21}} \cdot a_{\mathrm{32}} \cdot a_{\mathrm{13}} +
a_{\mathrm{31}} \cdot a_{\mathrm{12}} \cdot a_{\mathrm{23}} \\[-10pt]
&\phantom{=} - a_{\mathrm{31}} \cdot a_{\mathrm{22}} \cdot a_{\mathrm{13}} -
a_{\mathrm{21}} \cdot a_{\mathrm{12}} \cdot a_{\mathrm{33}} -
a_{\mathrm{11}} \cdot a_{\mathrm{32}} \cdot a_{\mathrm{23}}](../_images/math/396d409978ca48e8d5126cbf4a44610b198ac667.png)
Wiederum lässt sich die Determinante nach der Regel von Sarrus berechnen, indem man die Produkte der in der „Hauptdiagonale“ stehenden Zahlen (von links oben nach rechts unten) bildet und davon die Produkte der in der „Nebendiagonalen“ stehenden Zahlen (von links unten nach rechts oben) subtrahiert. Ist die resultierende Zahl ungleich Null, so ist das Gleichungssystem eindeutig lösbar.
Die Lösungen für 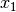 ,
, 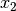 und
und 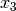 lassen sich ebenfalls
nach der Regel von Cramer in Determinanten-Schreibweise darstellen. Im Nenner
steht wiederum die eigentliche Determinante des Gleichungssystems, im Zähler
wird die erste, zweite beziehungsweise dritte Spalte der Determinante durch die
rechte Seite der Gleichung ersetzt. Somit gilt:
lassen sich ebenfalls
nach der Regel von Cramer in Determinanten-Schreibweise darstellen. Im Nenner
steht wiederum die eigentliche Determinante des Gleichungssystems, im Zähler
wird die erste, zweite beziehungsweise dritte Spalte der Determinante durch die
rechte Seite der Gleichung ersetzt. Somit gilt:
(4)¶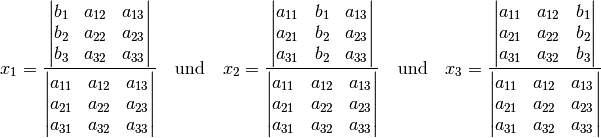
Mehrreihige Determinanten
Auch Gleichungssysteme mit mehr als drei Gleichungen und Unbekannten lassen sich
mit der obigen Determinantenmethode (Regel von Cramer) lösen. Dazu müssen
Determinanten mit 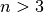 Reihen berechnet werden. Möchte man für solche
Determinanten eine allgemeine Lösungsregel angeben, so werden die dabei
auftretenden Terme jedoch schnell unübersichtlich: Eine Erweiterung der Regel
von Sarrus auf
Reihen berechnet werden. Möchte man für solche
Determinanten eine allgemeine Lösungsregel angeben, so werden die dabei
auftretenden Terme jedoch schnell unübersichtlich: Eine Erweiterung der Regel
von Sarrus auf  -reihige Determinanten enthält allgemein
-reihige Determinanten enthält allgemein  Summanden, bei einer
Summanden, bei einer  -reihigen Determinante müssten also bereits
-reihigen Determinante müssten also bereits
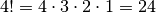 Summanden ausgewertet werden , bei
einer
Summanden ausgewertet werden , bei
einer 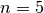 -reihigen Determinante sogar
-reihigen Determinante sogar 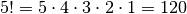 .
.
Einfacher ist es im allgemeinen, aus einer  -reihigen Determinante
insgesamt
-reihigen Determinante
insgesamt  Determinanten mit
Determinanten mit  Reihen zu bilden. Dieses
rekursive Entwlicklungsschema, das auch von Computer-Algebra-Systemen zur
Berechnung beliebig großer Determinanten genutzt wird, soll hier am Beispiel
einer vierreihigen Determinante vorgestellt werden.
Reihen zu bilden. Dieses
rekursive Entwlicklungsschema, das auch von Computer-Algebra-Systemen zur
Berechnung beliebig großer Determinanten genutzt wird, soll hier am Beispiel
einer vierreihigen Determinante vorgestellt werden.
Definition:
Streicht man in einer Determinanteeine beliebige Zeile
und eine beliebige Spalte
, so bezeichnet man die übrigbleibenden Elemente als Unterdeterminante
. Das Element
, das sich am Schnittpunkt beider Linien befindet, nennt man Schnittpunktelement.
Definition:
Multipliziert man den Wert der Unterdeterminante
mit dem Faktor
, so spricht man von der zum Element
adjungierten Unterdeterminante
:
(5)¶
Das Vorzeichen des Faktors 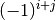 hängt von der Zeilen- und
Spaltennummer von
hängt von der Zeilen- und
Spaltennummer von 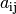 ab; ist die Summe beider Zahlen
gerade, so ist das Vorzeichen positiv, andernfalls negativ. Anschaulich kann man
das Vorzeichen auch anhand einer schachbrettartigen Vorzeichentabelle ablesen.
ab; ist die Summe beider Zahlen
gerade, so ist das Vorzeichen positiv, andernfalls negativ. Anschaulich kann man
das Vorzeichen auch anhand einer schachbrettartigen Vorzeichentabelle ablesen.
Mit den beiden obigen Definitionen kann der so genannte Entwicklungssatz von Leibniz folgendermaßen formuliert werden:
„Multipliziert man die Elemente einer beliebigen Reihe mit den jeweiligen adjungierten Unterdeterminanten und addiert die so entstehenden Produkte, so erhält man den Wert der Determinante.“
Es ist frei wählbar, nach welcher Reihe (Zeile oder Spalte) man eine
Determinante entwickelt. Entwickelt man eine Determinante 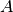 nach der
nach der
 -ten Zeile, so gilt:
-ten Zeile, so gilt:
Entwickelt man eine Determinante 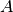 hingegen nach der
hingegen nach der 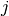 -ten
Spalte, so gilt:
-ten
Spalte, so gilt:
Zweckmäßig ist es, für die Entwicklung eine Reihe zu wählen, die möglichst viele Nullen enthält.
Beispiel:
Folgende Determinante
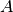 mit
mit  Reihen soll berechnet werden:
Reihen soll berechnet werden: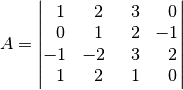
Zunächst wird die Determinante in Unterdeterminanten mit
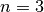 Reihen
entwickelt. Vorteilhaft ist hierbei eine Entwicklung nach der vierten Spalte,
da diese zwei Nullen enthält. Nach dem Leibnizschen Entwicklungssatz gilt:
Reihen
entwickelt. Vorteilhaft ist hierbei eine Entwicklung nach der vierten Spalte,
da diese zwei Nullen enthält. Nach dem Leibnizschen Entwicklungssatz gilt: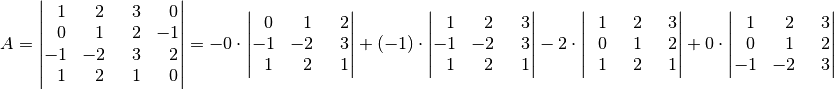
Alle Determinanten liefern reelle Zahlen als Ergebnisse; mit Null multipliziert ergeben sie ebenfalls Null. Es müssen somit nur die zweite und die dritte Unterdeterminante ausgewertet werden. Hierzu kann die Regel von Sarrus genutzt werden:
![A &= (-1) \cdot \begin{vmatrix}
\;\,\, 1 & \;\,\, 2 & \;\,\, 3 \\
-1 & -2 & \;\,\, 3 \\
\;\,\, 1 & \;\,\, 2 & \;\,\, 1
\end{vmatrix} - 2 \cdot \begin{vmatrix}
\;\,\, 1 & \;\,\, 2 & \;\,\, 3 \\
\;\,\, 0 & \;\,\, 1 & \;\,\, 2 \\
\;\,\, 1 & \;\,\, \;\,\, 1 & \;\,\, 2 & \;\,\, 1 \end{vmatrix} \\[5pt]
&= (-1) \cdot \qquad \quad \; 0 \qquad \; - 2 \cdot \qquad (-2) \qquad \quad = 4](../_images/math/eec6e8ffde8e0d710b4a0dd8c65a9eb57717358a.png)
Die Determinante
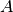 hat somit den Wert
hat somit den Wert 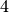 .
.
Um ein lineares Gleichungssystem mit  Gleichungen und Unbekannten zu
lösen, müssen neben der Determinante
Gleichungen und Unbekannten zu
lösen, müssen neben der Determinante 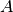 der Koeffizienten
der Koeffizienten
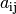 auch die
auch die  Determinanten
Determinanten 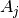 berechnet
werden, die sich ergeben, wenn man die
berechnet
werden, die sich ergeben, wenn man die 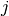 -te Spalte von
-te Spalte von 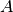 durch
die Ergebnisspalte
durch
die Ergebnisspalte 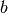 ersetzt. Für die Lösung
ersetzt. Für die Lösung 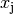 gilt
dann mit
gilt
dann mit 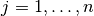 :
:
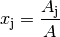
Voraussetzung ist bei dieser allgemeinen Regel von Cramer wiederum, dass die
Determinante 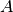 der Koeffizienten ungleich Null ist.
der Koeffizienten ungleich Null ist.
Determinanten-Regeln
Zum Rechnen mit Determinanten sind zudem folgende Regeln bisweilen nützlich:
- Der Wert einer Determinante bleibt gleich, wenn man sie transponiert, also die Zeilen mit den Spalten vertauscht.
Vertauscht man zwei Zeilen miteinander, so ändert sich das Vorzeichen der Determinante. Ebenso ändert sich das Vorzeichen einer Determinante, wenn man zwei Spalten vertauscht.
Der Wert einer Determinante bleibt gleich, wenn die Elemente einer Zeile mit einem beliebigen Faktor multipliziert und das Ergebnis zu den entsprechenden Elementen einer anderen Zeile addiert.
Das gleiche gilt, wenn man die mit einem beliebigen Faktor multiplizierten Elemente einer Spalte zu den entsprechenden Elementen einer anderen Spalte addiert.
Eine Determinante hat den Wert Null, wenn alle Elemente einer Zeile oder Spalte gleich Null sind oder wenn je zwei Zeilen beziehungsweise Spalten gleich oder zueinander proportional sind.
Eine Determinante wird mit einem Faktor multipliziert, indem man alle Elemente einer einzelnen Zeile oder einer einzelnen Spalte mit diesem Faktor multipliziert.
Hinweis
Zu diesem Abschnitt gibt es Übungsaufgaben.

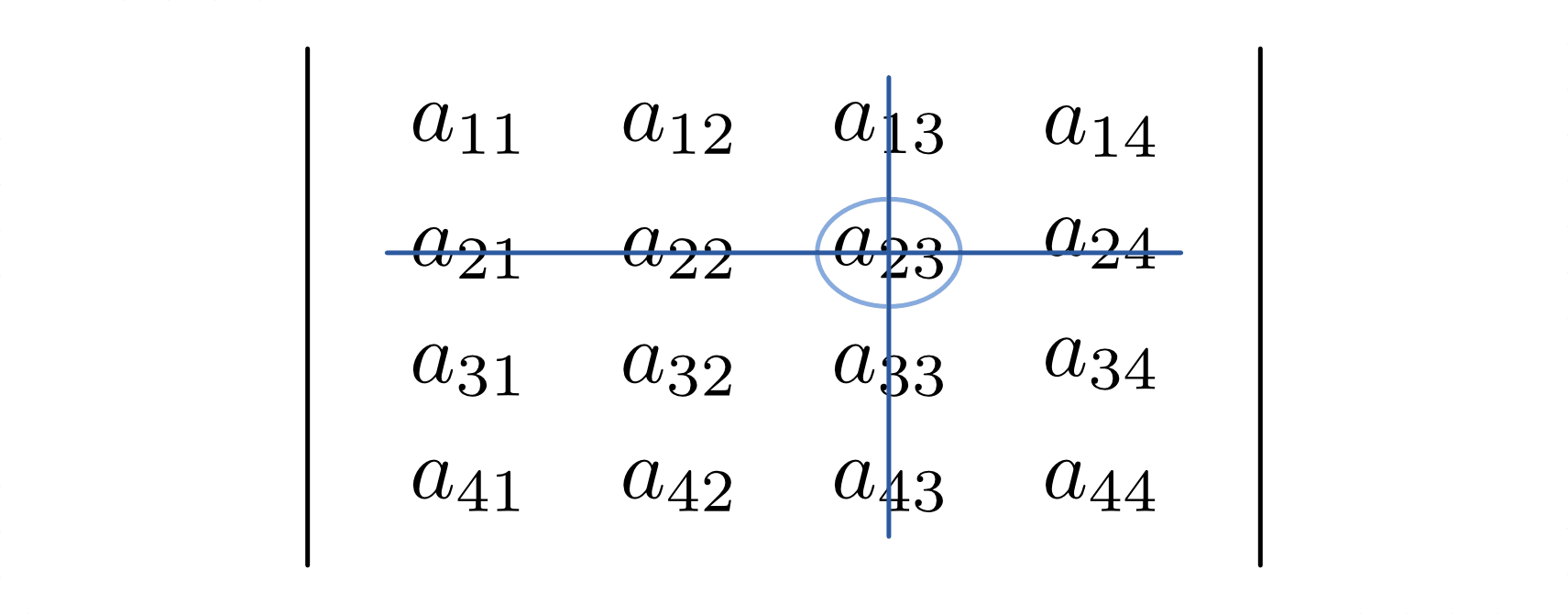
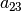 bei Streichung der zweiten Zeile
und der dritten Spalte.
bei Streichung der zweiten Zeile
und der dritten Spalte.