Kurvendiskussion¶
Als Kurvendiskussion bezeichnet man eine analytische Untersuchung einer gegebenen Funktion, um anhand charakteristischer Eigenschaften auf ihren Verlauf schließen zu können.
Dabei geht man, unabhängig von der Art der Funktion, immer nach einem im
Wesentlichen gleichen Schema vor. Dieses Schema soll im Folgenden anhand der
Beispielfunktion 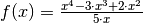 im Detail vorgestellt werden.
im Detail vorgestellt werden.
1.: Bestimmung des Definitionsbereichs
Zunächst muss überprüft werden, für welche  -Werte die Funktion
definiert ist; beispielsweise muss ausgeschlossen werden können, dass durch Null
dividiert wird.
-Werte die Funktion
definiert ist; beispielsweise muss ausgeschlossen werden können, dass durch Null
dividiert wird.
Die  -Werte dürfen zudem nicht außerhalb des Definitionsbereichs der
jeweiligen Funktion liegen, beispielsweise muss darauf geachtet werden, dass die
Argumente von Wurzel- oder Logarithmusfunktionen nicht negativ werden.
Potenzfunktionen der Form
-Werte dürfen zudem nicht außerhalb des Definitionsbereichs der
jeweiligen Funktion liegen, beispielsweise muss darauf geachtet werden, dass die
Argumente von Wurzel- oder Logarithmusfunktionen nicht negativ werden.
Potenzfunktionen der Form  mit
mit 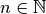 , ganzrationale Funktionen, Exponentialfunktionen sowie die
Sinus- und Cosinusfunktion sind für
alle reelle Zahlen definiert, bei ihnen gilt also
, ganzrationale Funktionen, Exponentialfunktionen sowie die
Sinus- und Cosinusfunktion sind für
alle reelle Zahlen definiert, bei ihnen gilt also 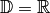 .
.
Der Definitionsbereich einer zusammengesetzten Funktion ist gleich der Schnittmenge der Definitionsbereiche aller Teilfunktionen.
Beispiel:
Die Funktion
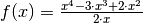 hat an der Stelle
hat an der Stelle 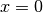 eine Definitionslücke, da für diesen Wert
der Nenner der Funktion gleich Null wird. Für alle anderen
eine Definitionslücke, da für diesen Wert
der Nenner der Funktion gleich Null wird. Für alle anderen  -Werte
ist die Funktion definiert, es ist also
-Werte
ist die Funktion definiert, es ist also 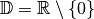 .
.
2.: Bestimmung des Verhaltens an den Rändern des Definitionsbereichs
Sofern der Definitionsbereich der zu untersuchenden Funktion es zulässt, werden
als nächstes die Grenzwerte der Funktion für
unendlich große positive und negative  -Werte untersucht. Bei Wurzel-
und Logarithmusfunktionen allerdings kann beispielsweise nur der Grenzwert für
unendlich große positive
-Werte untersucht. Bei Wurzel-
und Logarithmusfunktionen allerdings kann beispielsweise nur der Grenzwert für
unendlich große positive  -Werte bestimmt werden, da diese beiden
Funktionstypen nur für positive reelle Zahlen definiert sind.
-Werte bestimmt werden, da diese beiden
Funktionstypen nur für positive reelle Zahlen definiert sind.
Hat die Funktion Definitionslücken, so sind auch die Grenzwerte der Funktion an diesen Stellen zu bestimmen.
Beispiel:
Die Funktion
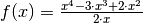 geht für sehr große positive
geht für sehr große positive  -Werte gegen Unendlich, da in diesem
Fall sowohl der Zähler wie auch der Nenner positive Werte annehmen, aber der
Zähler schneller wächst als der Nenner. Es gilt also:
-Werte gegen Unendlich, da in diesem
Fall sowohl der Zähler wie auch der Nenner positive Werte annehmen, aber der
Zähler schneller wächst als der Nenner. Es gilt also: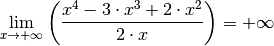
Für sehr große negative
 -Werte geht die Funktion gegen minus
Unendlich, da in diesem Fall die höchste Potenz des Zählers einen positiven
Wert, der Nenner aber einen negativen Wert liefert, und der Zähler schneller
wächst als der Nenner. Es gilt also:
-Werte geht die Funktion gegen minus
Unendlich, da in diesem Fall die höchste Potenz des Zählers einen positiven
Wert, der Nenner aber einen negativen Wert liefert, und der Zähler schneller
wächst als der Nenner. Es gilt also: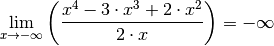
Die Funktion hat zudem
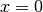 als Definitionslücke. Um die Grenzwerte
für
als Definitionslücke. Um die Grenzwerte
für 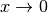 zu berechnen, kann man folgenden Trick nutzen: An jeder
Stelle
zu berechnen, kann man folgenden Trick nutzen: An jeder
Stelle 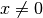 kann im Funktionsterm
kann im Funktionsterm  gekürzt werden, da
gekürzt werden, da
 als gemeinsamer Faktor in jedem Zählerterm enthalten ist. Somit
gilt:
als gemeinsamer Faktor in jedem Zählerterm enthalten ist. Somit
gilt: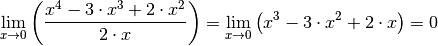
Sowohl für sehr kleine negative wie für sehr kleine positive
 -Werte
gehen alle Terme beim betrachteten Grenzwert gegen Null. Da der linksseitige
und der rechtsseitige Grenzwert identisch sind, ist die Funktion „stetig
behebbar“: Man könnte die Funktion abschnittsweise mit
-Werte
gehen alle Terme beim betrachteten Grenzwert gegen Null. Da der linksseitige
und der rechtsseitige Grenzwert identisch sind, ist die Funktion „stetig
behebbar“: Man könnte die Funktion abschnittsweise mit 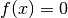 für
für
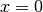 und
und 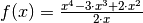 für
für 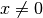 definieren, um eine „nahtlose“ Funktion zu erhalten,
die für alle reellen Zahlen definiert ist.
definieren, um eine „nahtlose“ Funktion zu erhalten,
die für alle reellen Zahlen definiert ist.
Die Regel von L’Hospital
In manchen Fällen erhält man bei der Bestimmung des Grenzwerts an einer
Definitionslücke  ein nicht bestimmtes Ergebnis, beispielsweise bei
der Funktion
ein nicht bestimmtes Ergebnis, beispielsweise bei
der Funktion 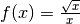 . Diese Funktion hat an der Stelle
. Diese Funktion hat an der Stelle
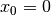 eine Definitionslücke, da der Nenner an dieser Stelle den Wert
Null annimmt; gleichzeitig ist allerdings auch der Zähler
eine Definitionslücke, da der Nenner an dieser Stelle den Wert
Null annimmt; gleichzeitig ist allerdings auch der Zähler 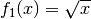 an dieser Stelle gleich Null. In derartigen Fällen, wenn sich ein
Grenzwert der Form
an dieser Stelle gleich Null. In derartigen Fällen, wenn sich ein
Grenzwert der Form 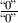 ergibt,
kann die sogenannte „Regel von L’Hospital“
angewendet werden:
ergibt,
kann die sogenannte „Regel von L’Hospital“
angewendet werden:
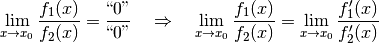
Für das oben genannte Beispiel 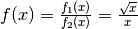 gilt:
gilt:
![f_1'(x) &= \left(x^{\frac{1}{2}}\right)' = \frac{1}{2} \cdot
x^{-\frac{1}{2}} \quad \text{und} \\[4pt]
f_2'(x) &= \;\left(x ^1 \right)'\; = 1](../../_images/math/fcfc3b6bf1048f0460bc36f1625bf76b725b7019.png)
Für die Stelle  gilt somit
gilt somit 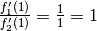 , der Grenzwert der Funktion für
, der Grenzwert der Funktion für 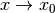 ist also
gleich
ist also
gleich 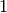 .
.
Haben also zwei Funktionen 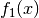 und
und  an einer Stelle
an einer Stelle
 beide den Grenzwert
beide den Grenzwert  , so besagt die Regel von L’Hospital,
dass in diesem Fall der Grenzwert gleich dem Quotienten der Ableitungen von
, so besagt die Regel von L’Hospital,
dass in diesem Fall der Grenzwert gleich dem Quotienten der Ableitungen von
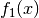 und
und  ist, sofern beide Funktionen differenzierbar
sind und die Ableitung der Nennerfunktion an der Stelle
ist, sofern beide Funktionen differenzierbar
sind und die Ableitung der Nennerfunktion an der Stelle  nicht gleich
Null ist.
nicht gleich
Null ist.
Die Regel von L’Hospital kann ebenfalls angewendet werden, wenn 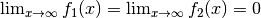 ist:
ist:
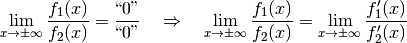
Weiterhin gilt die Regel von L’Hospital auch, wenn die Grenzwerte von
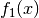 und
und  beide für
beide für 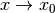 oder
oder 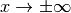 gegen Unendlich gehen:
gegen Unendlich gehen:
![\lim_{x \to x_0} \frac{f_1(x)}{f_2(x)} &=
\frac{\text{\enquote{$\infty$}}}{\text{\enquote{$\infty$}}} \quad \Rightarrow
\quad \;\;\lim_{x \to x_0} \frac{f_1(x)}{f_2(x)} = \;\;\lim_{x \to x_0}
\frac{f_1'(x)}{f_2'(x)} \\[6pt]
\lim_{x \to \pm \infty} \frac{f_1(x)}{f_2(x)} &=
\frac{\text{\enquote{$\infty$}}}{\text{\enquote{$\infty$}}} \quad \Rightarrow
\quad \lim_{x \to \pm \infty} \frac{f_1(x)}{f_2(x)} = \lim_{x \to \pm
\infty} \frac{f_1'(x)}{f_2'(x)}](../../_images/math/defc7d0ac9bc76457d062cbe7347df611399cedd.png)
Die Regel von L’Hospital ist somit in vielen Fällen nützlich, wenn ein Grenzwert auf andere Weise nicht bestimmt werden kann.
3.: Untersuchung auf Symmetrie
Eine Funktion ist achsensymmetrisch zur  -Achse, wenn
-Achse, wenn 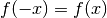 für alle
für alle  -Werte des Definitionsbereichs gilt. Dies ist der Fall,
wenn alle im Funktionsterm auftretenden Potenzen gerade sind.
-Werte des Definitionsbereichs gilt. Dies ist der Fall,
wenn alle im Funktionsterm auftretenden Potenzen gerade sind.
Eine Funktion ist punktsymmetrisch zum Koordinatenursprung 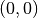 , wenn
, wenn
 für alle
für alle  -Werte des Definitionsbereichs gilt.
Dies ist der Fall, wenn alle im Funktionsterm auftretenden Potenzen ungerade
sind.
-Werte des Definitionsbereichs gilt.
Dies ist der Fall, wenn alle im Funktionsterm auftretenden Potenzen ungerade
sind.
Enthält eine Funktion Terme mit sowohl geraden wie auch ungeraden Exponenten, liegt keine Symmetrie vor.
Beispiel:
Die Funktion
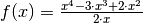 hat Terme mit sowohl geraden wie auch ungeraden Exponenten, sie ist somit
nicht symmetrisch.
hat Terme mit sowohl geraden wie auch ungeraden Exponenten, sie ist somit
nicht symmetrisch.
4.: Bestimmung von Nullstellen
Als Nullstellen bezeichnet man diejenigen  -Werte, deren
zugehörige Funktionswerte gleich Null sind, für die also
-Werte, deren
zugehörige Funktionswerte gleich Null sind, für die also 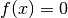 gilt.
gilt.
Beispiel:
Bei der Funktion
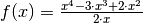 als gebrochen-rationaler Funktion entsprechen die Nullstellen den Nullstellen
des Zählers. Es muss somit geprüft werden, für welche
als gebrochen-rationaler Funktion entsprechen die Nullstellen den Nullstellen
des Zählers. Es muss somit geprüft werden, für welche  -Werte der
Term
-Werte der
Term 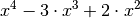 gleich Null ist, also folgende
Gleichung gelöst werden:
gleich Null ist, also folgende
Gleichung gelöst werden:
Auf der linken Seite kann
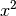 als gemeinsamer Faktor ausgeklammert
werden. Es folgt:
als gemeinsamer Faktor ausgeklammert
werden. Es folgt: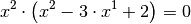
Ein Produkt ist gleich Null, wenn einer der Faktoren gleich Null ist. Es wäre somit
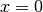 eine Nullstelle des Zählers, doch dieser Wert ist nicht in
der Definitionsmenge der Funktion enthalten. Zu untersuchen bleibt, für
welche
eine Nullstelle des Zählers, doch dieser Wert ist nicht in
der Definitionsmenge der Funktion enthalten. Zu untersuchen bleibt, für
welche  -Werte der zweite Faktor
-Werte der zweite Faktor 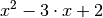 gleich
Null wird:
gleich
Null wird:
Diese Gleichung kann mit Hilfe der Lösungsformel für quadratische Gleichungen gelöst werden. Mit
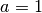 ,
,  und
und 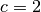 folgt:
folgt: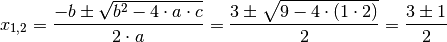
Die Funktion hat also die zwei Nullstellen
 und
und 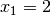 .
.
5.: Bestimmung von Extremstellen
Bei der Untersuchung von Extremstellen wird geprüft, für
welche  -Werte der Funktionsgraph Hochpunkte, Tiefpunkte oder
Terrassenpunkte besitzt. Hierzu muss die erste Ableitung der Funktion bestimmt
und gleich Null gesetzt werden. Um zu prüfen, um welchen Extremstellen-Typ es
sich handelt, kann man zu jeder Extremstelle
-Werte der Funktionsgraph Hochpunkte, Tiefpunkte oder
Terrassenpunkte besitzt. Hierzu muss die erste Ableitung der Funktion bestimmt
und gleich Null gesetzt werden. Um zu prüfen, um welchen Extremstellen-Typ es
sich handelt, kann man zu jeder Extremstelle  einen etwas kleineren
und einen etwas größeren
einen etwas kleineren
und einen etwas größeren  -Wert in die erste Ableitungsfunktion
-Wert in die erste Ableitungsfunktion
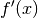 einsetzen und aus den erhaltenen Steigungswerten den
Krümmungsverlauf betrachten: Beispielsweise bedeutet eine erst positive und dann
negative Steigung einen Hochpunkt an der Stelle
einsetzen und aus den erhaltenen Steigungswerten den
Krümmungsverlauf betrachten: Beispielsweise bedeutet eine erst positive und dann
negative Steigung einen Hochpunkt an der Stelle  .
.
Eine zweite Möglichkeit zur Bestimmung des Nullstellentyps bietet die zweite
Ableitungsfunktion 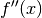 . Da man diese für eine Bestimmung der
Wendepunkte ohnehin berechnen muss, kann man dies auch gleich an dieser Stelle
tun und die
. Da man diese für eine Bestimmung der
Wendepunkte ohnehin berechnen muss, kann man dies auch gleich an dieser Stelle
tun und die  -Werte der Extremstellen einsetzen. Ergibt sich für eine
Stelle
-Werte der Extremstellen einsetzen. Ergibt sich für eine
Stelle  ein positiver Wert, so handelt es sich um einen Tiefpunkt,
ergibt sich ein negativer Wert, so handelt es sich um einen Hochpunkt. Ergibt
sich der Wert Null, so handelt es sich um einen Terrassenpunkt.[1]
ein positiver Wert, so handelt es sich um einen Tiefpunkt,
ergibt sich ein negativer Wert, so handelt es sich um einen Hochpunkt. Ergibt
sich der Wert Null, so handelt es sich um einen Terrassenpunkt.[1]
Die zu den Extremstellen gehörenden Funktionswerte erhält man durch Einsetzen
in die ursprüngliche Funktion  .
.
Beispiel:
Für
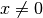 kann die Funktion
kann die Funktion 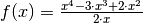 als
als 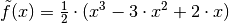 geschrieben werden. Die erste Ableitung dieser
Funktion lautet:
geschrieben werden. Die erste Ableitung dieser
Funktion lautet:
Diese (Ableitungs-)Funktion ist gleich Null, wenn der Term
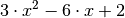 gleich Null ist:
gleich Null ist: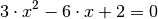
Diese Gleichung kann mit Hilfe der Lösungsformel für quadratische Gleichungen gelöst werden. Mit
 ,
, 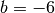 und
und 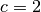 folgt:
folgt: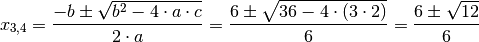
Die Funktion besitzt also die zwei Extremstellen
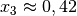 und
und
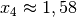 . Um zu überprüfen, um welche Art von Extremstellen
es sich handelt, wird die zweite Ableitung berechnet:
. Um zu überprüfen, um welche Art von Extremstellen
es sich handelt, wird die zweite Ableitung berechnet: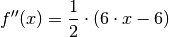
Für
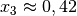 ergibt sich beim Einsetzen ein Wert kleiner als
Null, die Funktion hat an dieser Stelle also einen Hochpunkt. Für
ergibt sich beim Einsetzen ein Wert kleiner als
Null, die Funktion hat an dieser Stelle also einen Hochpunkt. Für 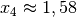 ergibt sich beim Einsetzen ein Wert größer als Null, die
Funktion hat an dieser Stelle also einen Tiefpunkt.
ergibt sich beim Einsetzen ein Wert größer als Null, die
Funktion hat an dieser Stelle also einen Tiefpunkt.Ein Einsetzen von
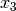 und
und 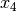 in die Funktion
in die Funktion  ergibt die zugehörigen Funktionswerte
ergibt die zugehörigen Funktionswerte 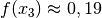 und
und
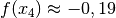 .
.
6.: Bestimmung von Wendepunkten
Bei der Untersuchung hinsichtlich Wendepunkten wird
geprüft, für welche  -Werte die zweite Ableitung der Funktion gleich
Null ist. Hat man eine (oder mehrere) solche Stelle
-Werte die zweite Ableitung der Funktion gleich
Null ist. Hat man eine (oder mehrere) solche Stelle  gefunden, kann
man anschließend durch Einsetzen eines etwas kleineren und eines etwas größeren
gefunden, kann
man anschließend durch Einsetzen eines etwas kleineren und eines etwas größeren
 -Werts in die zweite Ableitungsfunktion
-Werts in die zweite Ableitungsfunktion 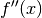 prüfen, ob die
jeweiligen Ergebnisse ein unterschiedliches Vorzeichen besitzen. In diesem Fall
handelt es sich tatsächlich um einen Wendepunkt, andernfalls nicht.
prüfen, ob die
jeweiligen Ergebnisse ein unterschiedliches Vorzeichen besitzen. In diesem Fall
handelt es sich tatsächlich um einen Wendepunkt, andernfalls nicht.
Beispiel:
Für
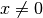 kann die Funktion
kann die Funktion 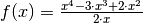 als
als 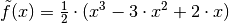 geschrieben werden. Die zweite Ableitung dieser
Funktion lautet:
geschrieben werden. Die zweite Ableitung dieser
Funktion lautet: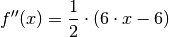
Setzt man diese Funktionsgleichung gleich Null, so erhält man
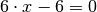 oder
oder 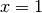 als einzige Wendestelle des Funktionsgraphen.
als einzige Wendestelle des Funktionsgraphen.Dass es sich tatsächlich um eine Wendestelle handelt, kann durch Einsetzen beispielsweise der Werte
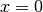 und
und  in die zweite Ableitung
in die zweite Ableitung
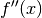 überprüft werden: Es ist
überprüft werden: Es ist 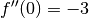 und
und
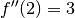 , die Krümmung ändert also bei
, die Krümmung ändert also bei 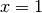 ihr Vorzeichen,
somit hat der Funktionsgraph dort eine Wendestelle.
ihr Vorzeichen,
somit hat der Funktionsgraph dort eine Wendestelle.Setzt man
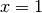 in die ursprüngliche Funktion
in die ursprüngliche Funktion  ein, erhält
man
ein, erhält
man 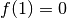 . Die Funktion hat also einen Wendepunkt bei
. Die Funktion hat also einen Wendepunkt bei 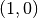 .
.
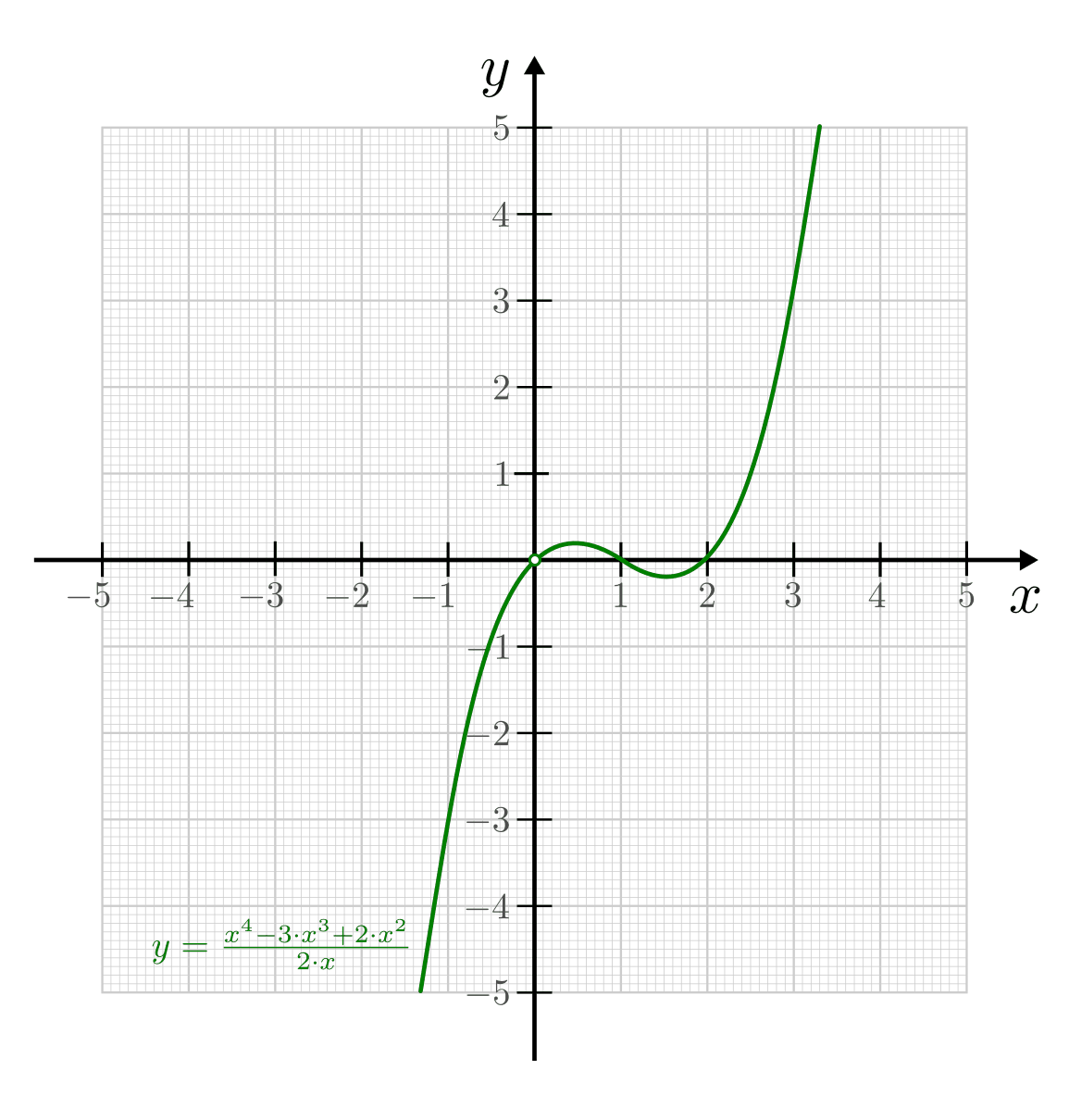
7.: Erstellung eines Funktionsgraphen
Die bis zu diesem Schritt im Rahmen der Kurvendiskussion erarbeiteten Ergebnisse
reichen grundsätzlich aus, um den Verlauf des Funktionsgraphen qualitativ
richtig zeichnen zu können; ergänzend können bei Bedarf einige weitere
 -Werte in die Funktion
-Werte in die Funktion  eingesetzt werden, um weitere
Punkte des Funktionsgraphen zu erhalten.
eingesetzt werden, um weitere
Punkte des Funktionsgraphen zu erhalten.
Beispiel:
Bei der Funktion
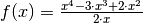 sind nach den vorherigen Rechenschritten die
Nullstellen, Extrem- und Wendestellen sowie das Verhalten im Unendlichen
bekannt. Der Funktionsgraph sieht damit etwa so aus:
sind nach den vorherigen Rechenschritten die
Nullstellen, Extrem- und Wendestellen sowie das Verhalten im Unendlichen
bekannt. Der Funktionsgraph sieht damit etwa so aus:
Das genannte Schema für Kurvendiskussionen lässt sich allgemein für beliebige Kombinationen elementarer Funktionen anwenden.
Anmerkungen:
| [1] | Als einfache Merkregel kann man an die Normalparabel 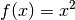 denken. Deren erste Ableitung ist
denken. Deren erste Ableitung ist 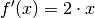 , die zweite
Ableitung ist , die zweite
Ableitung ist  . Die Normalparabel hat einen Tiefpunkt bei . Die Normalparabel hat einen Tiefpunkt bei
 , wobei der Wert der zweiten Ableitung an dieser Stelle positiv
ist. , wobei der Wert der zweiten Ableitung an dieser Stelle positiv
ist. |

 .
.