Mechanik der Festkörper, Flüssigkeiten und Gase¶
Mechanik der Festkörper¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Mechanik der Festkörper.
Beton hat eine hohe Druckfestigkeit, Stahl eine hohe Zugfestigkeit. Der Stahl muss folglich in die Unterseite des Betons eingebracht werden, weil dort Zugspannungen auftreten; ohne Stahl könnte der Beton auf der Unterseite auseinander brechen.
Mechanik der Flüssigkeiten¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Mechanik der Flüssigkeiten.
Statischer Druck
Der auf den Kolben ausgeübte Druck
 ist gleich dem Quotienten aus der
einwirkenden Kraft
ist gleich dem Quotienten aus der
einwirkenden Kraft  und der Querschnittsfläche
und der Querschnittsfläche  des Kolbens:
des Kolbens:![p = \frac{F}{A} = \frac{\unit[350]{N}}{\unit[0,01]{m^2}} = \unit[35 \cdot
10^3]{Pa} = \unit[0,35]{bar}](../../_images/math/eb5556c4b1de82db1a268731fd81518b69c4f3b7.png)
Im Gleichgewichtsfall, also bei einem sich nicht bewegenden Kolben, herrscht im Fluid innerhalb des Zylinders ein ebenso hoher Druck.
Der Schweredruck lässt sich mittels folgender Formel berechnen:
![p_{\mathrm{schwere}} = \rho_{\mathrm{Fl}} \cdot g \cdot h = \unit[1,0
\cdot 10^3]{\frac{kg}{m^3}} \cdot \unit[9,81]{\frac{N}{kg}} \cdot
\unit[10]{m} \approx \unit[98,1 \cdot 10^3]{Pa}](../../_images/math/1950205c863374c4a0041cc3bafe46b57f2d72fb.png)
Zur Umrechnung der angegebenen Dichte wurde die Einheits-Beziehung
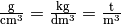 verwendet und
verwendet und ![\unit[1]{t} = \unit[10^3]{kg}](../../_images/math/b4a8584a6480b0f048cd9fa5cf4f1328ef04bcde.png) gesetzt.
gesetzt.Die Einheit des Ergebnisses in der obigen Gleichung folgt aus der Beziehung
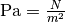 . Da
. Da ![\unit[1]{bar} = \unit[100]{kPa}](../../_images/math/abac5db62aee40bd1ce7154df1e6ac6d0c1090e7.png) ist, kann man sagen, dass der Schweredruck im Wasser je
ist, kann man sagen, dass der Schweredruck im Wasser je ![\unit[10]{m}](../../_images/math/5ab37424ac0a69b1ed26cd3ffad9b805b5bba0f2.png) Eintauchtiefe um rund
Eintauchtiefe um rund ![\unit[1]{bar}](../../_images/math/6e104f5aba80ffafeaa668badd6fbfaa9bf2a2be.png) zunimmt.
zunimmt.
Wasser hat eine Dichte von
![\rho = \unit[1]{\frac{g}{cm^3}} = \unit[1
\cdot 10^3]{\frac{kg}{m^3}}](../../_images/math/50efa88ff2dbfacd7f06b5c220ff99d9bea0ef5b.png) . In einer Leitung kann es so weit steigen, bis
der sich ergebende Schweredruck
. In einer Leitung kann es so weit steigen, bis
der sich ergebende Schweredruck 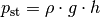 mit
mit 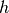 als Steighöhe ebenso groß ist wie in der Leitung herrschende
Wasserdruck
als Steighöhe ebenso groß ist wie in der Leitung herrschende
Wasserdruck ![p = \unit[6]{bar} = \unit[6 \cdot 10^5]{Pa}](../../_images/math/b5bddf4f275b1672f7e8752774dd572d0974083a.png) in Bodenhöhe:
in Bodenhöhe:![p &= \rho \cdot g \cdot h \quad \Longleftrightarrow \quad h =
\frac{p}{\rho \cdot g} \\[6pt]
h &= \frac{\unit[6 \cdot 10^5]{Pa}}{\unit[1 \cdot 10^3]{\frac{kg}{m^3}}
\cdot \unit[9,81]{\frac{N}{kg}}} \approx \unit[61,2]{m}](../../_images/math/6cb83049c15658af9d72ff025e847e08ef40c0eb.png)
Das Wasser kann somit rund
![\unit[61]{m}](../../_images/math/51791fbfc6f8c0c6966f354e67c03abf64975952.png) hoch steigen.
hoch steigen.
Statischer Auftrieb
Bei einem Volumen von
![V=\unit[80\,]{l}](../../_images/math/9d1a7ee5b0958dc8f27ae680ea444630852d4f92.png) und einer durchschnittlichen
Dichte von
und einer durchschnittlichen
Dichte von ![\rho_{\mathrm{K}}= \unit[1050]{\frac{kg}{m^3}} =
\unit[1,05]{\frac{kg}{dm^3}}](../../_images/math/5c4722ce381905c8b1ffeb6d1f39f5e36f61d346.png) hat der badende Mensch eine Masse von
hat der badende Mensch eine Masse von ![m =
\rho \cdot V = \unit[1,05]{\frac{kg}{l}} \cdot \unit[80]{l} = \unit[84]{kg}](../../_images/math/781518b528d54e7841c54dc0ba417eeb70318f63.png) und damit eine Gewichtskraft von
und damit eine Gewichtskraft von ![m \cdot g = \unit[80]{kg} \cdot
\unit[9,81]{\frac{N}{kg}} \approx \unit[824]{N}](../../_images/math/5d4b4e499bbca4f9f9d143a86d718cf417735cef.png) .
.Die Auftriebskraft
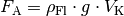 ist abhängig vom Volumen des eintauchenden Körpers, jedoch
nicht von dessen Dichte. Für reines Wasser ist
ist abhängig vom Volumen des eintauchenden Körpers, jedoch
nicht von dessen Dichte. Für reines Wasser ist ![\rho_{\mathrm{Fl}} =
\unit[1000]{\frac{kg}{m^3}} = \unit[1,00]{\frac{kg}{dm^3}}](../../_images/math/9b49f203ae027a0fc408f93e2e4e098e1f1d1ddd.png) , die
Auftriebskraft beträgt somit:
, die
Auftriebskraft beträgt somit:![F_{\mathrm{A,W}} = \rho_{\mathrm{Fl}} \cdot g \cdot V_{\mathrm{K}} =
\unit[1,00]{\frac{kg}{l}} \cdot \unit[9,81]{\frac{N}{kg}} \cdot
\unit[80]{l} \approx \unit[785]{N}.](../../_images/math/0d021cc36a98c181477114e880c9e10465d5a656.png)
In normalem Wasser hat der badende Mensch somit ein scheinbares Gewicht von
![F_{\mathrm{G}} - F_{\mathrm{A}} \approx \unit[39]{N}](../../_images/math/28dcb6a8b64cf70956117afac0fe71b21979ff39.png) ; ohne
Schwimmbewegungen würde der Körper also sinken.
; ohne
Schwimmbewegungen würde der Körper also sinken.In gesättigtem Salzwasser gilt mit
![\rho_{\mathrm{Fl}} =
\rho_{\mathrm{SW}} = \unit[1120]{\frac{kg}{m^3}} =
\unit[1,12]{\frac{kg}{dm^3}}](../../_images/math/1951e2fa20bb3eb44f990a2a9f027dc1bfb83622.png) :
:![F_{\mathrm{A,SW}} = \rho_{\mathrm{Fl}} \cdot g \cdot V_{\mathrm{K}} =
\unit[1,12]{\frac{kg}{l}} \cdot \unit[9,81]{\frac{N}{kg}} \cdot
\unit[80]{l} \approx \unit[879]{N}.](../../_images/math/b8cb1da389e8f4027e36860eda9e59cd31c6b981.png)
Im Salzwasser ist die Auftriebskraft des badenden Menschen um
![\unit[55]{N}](../../_images/math/1d4d00e1cbd3d4b0cf9d716425be84e94dd093b6.png) größer als seine Gewichtskraft; der Körper schwimmt also
auch ohne Schwimmbewegungen.
größer als seine Gewichtskraft; der Körper schwimmt also
auch ohne Schwimmbewegungen.
Um unterzutauchen, muss der Dichtewert eines Körpers größer sein als die Dichte der Flüssigkeit. Um abzutauchen, muss ein Fisch somit seinen Dichtewert erhöhen. Fische besitzen dazu eine Schwimmblase, die mit dem Kiemensystem verbunden ist. Um abzutauchen, entleeren sie diese Schwimmblase, um aufzutauchen, wird sie mit Gas aufgefüllt. Auf diese Weise können Fische ihr Volumen und somit ihre Dichte aktiv beeinflussen.
Unterseeboote haben nach dem gleichen Prinzip Wassertanks, die zum Absinken geflutet und zum Auftauchen mittels Pressluft entleert werden. Auf diese Weise kann ebenfalls die durchschnittliche Dichte des Bootes gesteuert werden.
Bernoulli-Gleichung
Mit der ersten Röhre wird nur der statische Druck, mit der hinteren der Gesamtdruck gemessen. Der in der hinteren Röhre zusätzlich auftretende dynamische Druck bewirkt einen stärkeren Anstieg der Flüssigkeitssäule. Im Gleichgewichtsfall entspicht der dynamische Druck
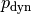 der strömenden Flüssigkeit dem zusäzlichen statischen Druck
der strömenden Flüssigkeit dem zusäzlichen statischen Druck
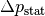 in der hinteren Flüssigkeitssäule:
in der hinteren Flüssigkeitssäule: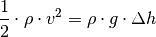
Die Dichte
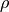 kürzt sich heraus, die Gleichung kann dann nach
kürzt sich heraus, die Gleichung kann dann nach
 aufgelöst werden:
aufgelöst werden:![v = \sqrt{2 \cdot g \cdot \Delta h} = \sqrt{2 \cdot
\unit[9,81]{\frac{m}{s^2}} \cdot \unit[0,1]{m}} \approx
\unit[1,4]{\frac{m}{s}}](../../_images/math/69345ce56c3b062a450fede2f1d9822fb1d610b6.png)
Im Extremfall wird der gesamte in der Wasserleitung herrschende statische Druck in den dynamischen Druck des ausströmenden Wassers umgewandelt. Man erhält damit als Gleichung:
![p = \frac{1}{2} \cdot \rho_{\mathrm{Fl}} \cdot v^2 \quad
\Longleftrightarrow \quad v = \sqrt{\frac{2 \cdot p}{\rho_{\mathrm{Fl}} }}
\approx \unit[14,14]{\frac{m}{s}}](../../_images/math/503a10ffa1c2c3065473385050e13cb9ec4a5370.png)
Diese Geschwindigkeit entspricht rund
![\unit[50]{\frac{km}{h}}](../../_images/math/48414adf3a029eec32818d28c358f8e41ca42bd7.png) .
.
Mechanik der Gase¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Mechanik der Gase.
Sowohl bei Flüssigkeiten als auch bei Gasen gilt für den dynamischen Druck
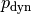 :
: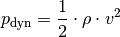
Setzt man hier
![p_{\mathrm{dyn}} = \unit[10]{kPa} = \unit[10 \cdot
10^3]{Pa}](../../_images/math/81ede0ba9ef7d0a2cb47e3b4fda126f18a92cd86.png) und für die Dichte
und für die Dichte 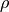 des Fluids
des Fluids
![\rho_{\mathrm{Wasser}} = \unit[1]{\frac{g}{cm^3}} =
\unit[1000]{\frac{kg}{m^3}}](../../_images/math/ab6559d4eaec0dbdb2c2a3cce0527e508205e286.png) beziehungsweise
beziehungsweise ![\rho_{\mathrm{Luft}} =
\unit[1,29]{\frac{kg}{m^3}}](../../_images/math/401a2c092ab5c7de1695fef0c9b91bef85b25329.png) ein, so folgt:
ein, so folgt:![v_{\mathrm{Wasser}} = \sqrt{\frac{2 \cdot
p_{\mathrm{dyn}}}{\rho_{\mathrm{Wasser}} }} = \sqrt{ \frac{2 \cdot
\unit[10 \cdot 10^3]{Pa}}{\unit[1000]{\frac{kg}{m^3}} }} \approx
\unit[4,47]{\frac{m}{s}}](../../_images/math/4a556d8cb76a50788deaf9ca072906c0cbbbd58c.png)
Die Einheit ergibt sich, da
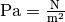 und
und
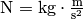 gilt; somit folgt:
gilt; somit folgt: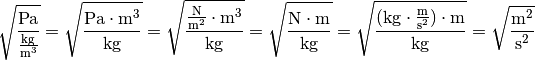
Für die nötige Strömungsgeschwindigkeit von Luft gilt entsprechend:
![v_{\mathrm{Wasser}} = \sqrt{\frac{2 \cdot
p_{\mathrm{dyn}}}{\rho_{\mathrm{Luft}} }} = \sqrt{ \frac{2 \cdot \unit[10
\cdot 10^3]{Pa}}{\unit[1,29]{\frac{kg}{m^3}} }} \approx
\unit[4,47]{\frac{m}{s}} \approx \unit[124,5]{\frac{m}{s}}](../../_images/math/d41002ab5e45a7e5a12e856554b2d5219c924568.png)
Die zur Erzeugung des gleichen dynamischen Drucks nötige Strömungsgeschwindigkeit ist bei Luft somit wesentlich höher als bei Wasser.
Da aufgrund der Kontinuitätsbedingung der Volumenstrom an allen Stellen gleich ist, gilt für die Geschwindigkeiten
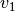 und
und 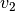 im
weiten und im engen Rohrstück:
im
weiten und im engen Rohrstück: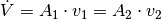
Setzt man für den Volumenstrom
![\dot{V} = \unit[1,5 \cdot
10^{-2}]{\frac{m^3}{min}} = \unit[2,5 \cdot 10 ^{-4}]{\frac{m^3}{s}}](../../_images/math/64ebf6ae3b915d84adeda268d2668386f1191c5e.png) ein, so
folgt mit
ein, so
folgt mit ![A_1 = \unit[2]{cm^2} = \unit[2 \cdot 10 ^{-4}]{m^2}](../../_images/math/0427c5718de0b4059eb44416c8eee1c8dcd6981b.png) und
und
![A_2 = \unit[0,5]{cm^2} = \unit[0,5 \cdot 10 ^{-4}]{m^2}](../../_images/math/6f3bba1423bf1ae8d02c46a22aaff037e7f29e21.png) :
:![v_1 &= \frac{\dot{V}}{A_1} = \frac{\unit[2,5 \cdot 10
^{-4}]{\frac{m^3}{s}}}{\unit[2 \cdot 10 ^{-4}]{m^2}}=
\unit[1,25]{\frac{m}{s}} \\
v_2 &= \frac{\dot{V}}{A_2} = \frac{\unit[2,5 \cdot 10
^{-4}]{\frac{m^3}{s}}}{\unit[0,5 \cdot 10 ^{-4}]{m^2}}=
\unit[5,0]{\frac{m}{s}} \\](../../_images/math/e795248ac6b81239f579b04428c84a55413d3590.png)
Nachdem die Strömungsgeschwindigkeiten bekannt sind, können nun die zugehörigen dynamischen Drücke
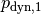 und
und
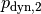 im weiten und engen Rohrstück berechnet werden:
im weiten und engen Rohrstück berechnet werden:![p_{\mathrm{dyn,1}} &= \frac{1}{2} \cdot \rho \cdot v_1^2 = \frac{1}{2}
\cdot \unit[1,32]{\frac{kg}{m^3}} \cdot
\left(\unit[1,25]{\frac{m}{s}}\right)^2 \approx \unit[1,03]{Pa} \\
p_{\mathrm{dyn,2}} &= \frac{1}{2} \cdot \rho \cdot v_2^2 = \frac{1}{2}
\cdot \unit[1,32]{\frac{kg}{m^3}} \cdot
\left(\unit[5,0\phantom{5}]{\frac{m}{s}}\right)^2 \approx \unit[16,5]{Pa}](../../_images/math/dee57811d7fbfd12d72771da815045939b4e7c60.png)
Da nach der Bernoulli-Gleichung der Gesamtdruck in beiden Rohrteilen gleich ist, muss im ersten, weiteren Rohrteil der statische Druck um
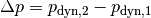 höher sein als im zweiten. Der
statische „Überdruck“, der am linken Ende des U-Rohrs anliegt, wird im
Gleichgewichtsfall durch zusätzlichen statischen Druck ausgeglichen, der sich
durch die zusätzliche Füllhöhe im rechten Teil des U-Rohrs ergibt. Es gilt
also:
höher sein als im zweiten. Der
statische „Überdruck“, der am linken Ende des U-Rohrs anliegt, wird im
Gleichgewichtsfall durch zusätzlichen statischen Druck ausgeglichen, der sich
durch die zusätzliche Füllhöhe im rechten Teil des U-Rohrs ergibt. Es gilt
also: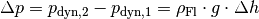
Diese Gleichung kann nach der gesuchten Größe
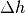 aufgelöst
werden:
aufgelöst
werden:![\Delta h = \frac{p_{\mathrm{dyn,2}}-
p_{\mathrm{dyn,1}}}{\rho_{\mathrm{Fl}} \cdot g} = \frac{\unit[16,5]{Pa} -
\unit[1,03]{Pa}}{\unit[1000]{\frac{kg}{m^3}} \cdot
\unit[9,81]{\frac{m}{s^2}}} \approx \unit[1,6 \cdot 10 ^{-3}]{m}](../../_images/math/af6331dd06e27fbdecd0faaf4a9eee11507c3547.png)
Der Höhenunterschied der Wasserstände im U-Rohr beträgt somit rund
![\unit[1,6]{mm}](../../_images/math/b59c8f5707c89ddd60c46fac767f221a58db6e61.png) .
.
Bei einer konstanten Sinkgeschwindigkeit müssen sich die wirkenden Kräfte – die nach unten gerichtete Gewichtskraft und die entgegengesetzt wirkende Luftwiderstands-Kraft – gegenseitig aufheben. Es muss also gelten:
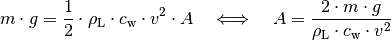
Für die (runde) Fallschirm-Fläche gilt
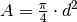 ;
für den Radius
;
für den Radius 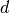 des Fallschirms ergibt sich somit:
des Fallschirms ergibt sich somit:![d = \sqrt{\frac{2 \cdot m \cdot g \cdot 4}{c_{\mathrm{w}} \cdot
\rho_{\mathrm{L}}\cdot \pi \cdot v^2 }} = \sqrt{\frac{8 \cdot
\unit[100]{kg} \cdot \unit[9,81]{\frac{N}{kg}}}{1,3 \cdot
\unit[1,2]{\frac{kg}{m^3}} \cdot \pi \cdot \left( \unit[8,0]{\frac{m}{s}}
\right)^2}} \approx \unit[5,0]{m}](../../_images/math/9babfa339ed03a1ac6208681b55ae1a4fe3ee8e6.png)
Die Einheit ergibt sich, wenn man
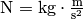 setzt:
setzt: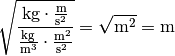
Der Fallschirm muss somit einen Durchmesser von rund
![\unit[5]{m}](../../_images/math/7f0402ed54213fe37ab62a24b9bd6191d76b2a9e.png) aufweisen.
aufweisen.
