Impuls und Drehimpuls¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Impuls und Drehimpuls.
Der Impuls
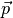 eines Körpers ist definiert als Produkt aus seiner Masse
eines Körpers ist definiert als Produkt aus seiner Masse
 und seiner Geschwindigkeit
und seiner Geschwindigkeit 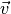 . Eine Taube mit einer
Masse von
. Eine Taube mit einer
Masse von ![m=\unit[20]{g} = \unit[0,02]{kg}](../_images/math/b934c32ba8be76004404c775791d4545a9f35d46.png) und einer Geschwindigkeit
von
und einer Geschwindigkeit
von ![v = \unit[75]{km/h} \approx \unit[20,8]{m/s}](../_images/math/7990cfffdd709f212c9d5ed8c7bd42e851eed414.png) hat somit folgenden
Impuls:
hat somit folgenden
Impuls:![p = m \cdot v = \unit[0,02]{kg} \cdot \unit[20,8]{\frac{m}{s}} \approx
\unit[0,42]{\frac{kg \cdot m}{s}}](../_images/math/0cc193257ac4ce111043e9eb51f5143643970ee2.png)
Der Impuls der Taube beträgt also rund
![\unit[0,42]{\frac{kg \cdot m}{s}}](../_images/math/13be68e0f0226be1b0d5a705b660ae993690b7f6.png)
Wenn der Eisenbahnwagen an die stehenden Wagen ankoppelt, bewegen sie sich, – wie bei jedem unelastischen Stoß – anschließend mit einer gemeinsamen Geschwindigkeit
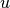 weiter. Diese kann mit Hilfe des
Impulserhaltungs-Satzes bestimmt werden.
weiter. Diese kann mit Hilfe des
Impulserhaltungs-Satzes bestimmt werden.Vor dem Stoß bewegt sich nur einer der Wagen mit einer Geschwindigkeit
![v_1=\unit[3]{m/s}](../_images/math/0a07a0d4495cfa7bd61f5786f23467d01e5d0335.png) und einer Masse
und einer Masse 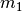 . Nach dem Stoß bewegen
sich alle vier Wagen der Geschwindigkeit Geschwindigkeit
. Nach dem Stoß bewegen
sich alle vier Wagen der Geschwindigkeit Geschwindigkeit 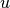 , ihre Masse
ist dabei
, ihre Masse
ist dabei 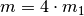 . Da der Gesamt-Impuls vor und nach dem Stoß
identisch ist, muss somit gelten:
. Da der Gesamt-Impuls vor und nach dem Stoß
identisch ist, muss somit gelten: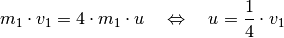
Die Wagen bewegen sich nach dem Ankoppeln also gemeinsam mit
![u =
\unit[0,75]{m/s}](../_images/math/319bbfe2a25606bbda3f60b80eb10ea9d9e35979.png) weiter.
weiter.
Vor dem (unelastischen) Zusammenprall haben die beiden Fahrzeuge mit den Massen
![m_1 = \unit[1000]{kg}](../_images/math/cf9acc4b9452b8da83a2b7f416d9ffe7917270c1.png) und
und ![m_2 = \unit[2000]{kg}](../_images/math/4293e4cc0b7f25952f3b9624b08ef9d32cd80fe8.png) und
den Geschwindigkeiten
und
den Geschwindigkeiten ![v_1 = \unitfrac[50]{km}{h} =
\unitfrac[13,9]{m}{s}](../_images/math/d6a46b05bafa3624622a62a330bfb841a7e26fb8.png) und
und ![v_2 = \unit[-50]{km}{h} =
\unit[-13,9]{m}{s}](../_images/math/4cb429f4ab8afd3d26912829114683772025041a.png) folgenden Gesamtimpuls:
folgenden Gesamtimpuls:![p = (m_1 \cdot v_2 + m_2 \cdot v_2) = \unit[1000]{kg} \cdot
\unit[13,9]{\frac{m}{s}} + \unit[2000]{kg} \cdot
(\unit[-13,9]{\frac{m}{s}}) = \unit[-13\,900]{\frac{kg \cdot m}{s}}](../_images/math/fd267070bcdb390c855b472ed6cb84ac220a3605.png)
Dieser Impuls bleibt nach dem Zusammenprall erhalten. Die Geschwindigkeit
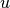 , mit der sich beide Fahrzeuge nach dem Stoß gemeinsam
weiterbewegen, kann berechnet werden, wenn man den Gesamtimpuls durch die
Gesamtmasse beider Fahrzeuge teilt:
, mit der sich beide Fahrzeuge nach dem Stoß gemeinsam
weiterbewegen, kann berechnet werden, wenn man den Gesamtimpuls durch die
Gesamtmasse beider Fahrzeuge teilt:![p = (m_1 + m_2) \cdot u \quad \Leftrightarrow \quad u = \frac{p}{m_1 +
m_2} \\[4pt]
\Rightarrow u = \frac{\unit[-13\,900]{\frac{kg \cdot
m}{s}}}{\unit[1000]{kg} + \unit[2000]{kg}} \approx
\unit[-4,63]{\frac{m}{s}}](../_images/math/87562eced5a3637bb004cf40e15a2adbe4f22698.png)
Die beiden Fahrzeuge bewegen sich unmittelbar nach dem Stoß also gemeinsam mit rund
![\unitfrac[-4,63]{m}{s} \approx \unitfrac[16,7]{km}{h}](../_images/math/7ee6d49e693071cb743322abcee5f8f5ebcdf390.png) in Richtung des
ersten (leichteren) Fahrzeugs.
in Richtung des
ersten (leichteren) Fahrzeugs.Der Fahrer des zweiten (schwereren) Fahrzeugs erfährt innerhalb des „Bremswegs“
![\Delta s = \unit[0,5]{m}](../_images/math/6d389f5edb382b4000481edaa47adb9e5080d830.png) (der Knautschzone) eine
Geschwindigkeitsänderung von
(der Knautschzone) eine
Geschwindigkeitsänderung von ![|v_1| = \unitfrac[13,9]{m}{s}](../_images/math/622565e7d12d5a4d01f0889352f21bcb3996e86c.png) auf
auf
![|v|=\unitfrac[4,93]{m}{s}](../_images/math/b1667552d2fd3d0058817e7cbdcb3ce49bf2dbc7.png) . Damit kann man mittels der Bremsformel die wirkende Beschleunigung folgendermaßen berechnen:
. Damit kann man mittels der Bremsformel die wirkende Beschleunigung folgendermaßen berechnen:![v^2 - v_2^2 = 2 \cdot a_2 \cdot \Delta s \quad \Longleftrightarrow \quad
a_2 = \frac{v^2 - v_2^2}{2 \cdot \Delta s}\\[6pt]
a_2 = \frac{\phantom{+}\unit[4,63^2]{\frac{m^2}{s^2}} -
\unit[13,9^2]{\frac{m^2}{s^2}}}{2 \cdot \unit[0,5]{m}} \approx
\unit[-171,5]{\frac{m}{s^2}}](../_images/math/7ffd98ed838de2f1566ba1f1f22dfab6175ea884.png)
Der Fahrer des ersten (leichteren) Fahrzeugs wird innerhalb des gleichen Bremswegs
![\Delta s = \unit[0,5]{m}](../_images/math/6d389f5edb382b4000481edaa47adb9e5080d830.png) (der Knautschzone des zweiten
Fahrzeugs) nicht nur von der Geschwindigkeit
(der Knautschzone des zweiten
Fahrzeugs) nicht nur von der Geschwindigkeit ![v_1 =
\unitfrac[+13,9]{m}{s}](../_images/math/33160681e6e14d9ddb80a115d6d8912f1da44f2b.png) bis zum Stillstand abgebremst, sondern zusätzlich
auf
bis zum Stillstand abgebremst, sondern zusätzlich
auf ![\unitfrac[-4,63]{m}{s}](../_images/math/3dd5b0025488c3d5de959bb56cc50aefef4e3c6d.png) beschleunigt. In der Bremsformel kann dies
explizit berücksichtigt werden, indem vor die Endgeschwindigkeit
beschleunigt. In der Bremsformel kann dies
explizit berücksichtigt werden, indem vor die Endgeschwindigkeit  ein
Minus-Zeichen gesetzt wird:
ein
Minus-Zeichen gesetzt wird:![a_1 = \frac{\unit[-4,63^2]{\frac{m^2}{s^2}} -
\unit[13,9^2]{\frac{m^2}{s^2}}}{2 \cdot \unit[0,5]{m}} \approx
\unit[-214,3]{\frac{m}{s^2}}](../_images/math/194e5ea94caaa53664a0ffc8ba857c6b451ea546.png)
Die Bremsformel berücksichtigt aufgrund der Quadrierung der Geschwindigkeitswerte nicht die ursprüngliche Richtung der Geschwindigkeiten, sondern vergleicht lediglich die Beträge der Start- und Endgeschwindigkeit: Ist die Endgeschwindigkeit geringer als die Startgeschwindigkeit, so ergibt sich ein negatives Vorzeichen. Dies bedeutet hierbei nur, dass die Beschleunigung entgegen der bisherigen Bewegungsrichtung verläuft; die physikalische Interpretation, ob die Beschleunigung „nach links“ oder „nach rechts“ gerichtet ist, muss man hingegen selbst treffen.
An den Beträgen der Beschleunigungen kann man erkennen, dass der Fahrer des schwereren Fahrzeugs beim Zusammenstoß eine geringere Bremsbeschleunigung erfährt der Fahrer des leichten Fahrzeugs; er hat also eine höhere Überlebenswahrscheinlichkeit.
Leichte Fahrzeuge gefährden zwar andere Verkehrsteilnehmer nur in geringerem Maße, sind aber bei Verkehrsunfällen gegenüber schweren Fahrzeugen benachteiligt. „Fair-Play“-Regelungen, wonach beispielsweise für schwere Fahrzeuge entsprechend striktere Regeln bezüglich Knautschzonen gelten müssten, konnten sich politisch bislang leider nicht durchsetzen.
