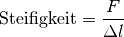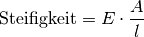Mechanik der Festkörper¶
Als Festkörper werden alle Körper bezeichnet, die im festen Aggregatzustand, also in einer kristallinen Struktur vorliegen. Hierzu gehören beispielsweise Metalle, Salze, Eis und zahlreiche organische Verbindungen. Bei Metallen und Salzen bestehen die einzelnen Bausteine des Kristallgitters aus Atomen, bei Eis und organischen Verbindungen aus Molekülen.
Die Festigkeit eines Kristalls hängt sowohl von den Bindungskräften zwischen den Atomen beziehungsweise Molekülen als auch von der räumlichen Anordnung ab:
- Diamant besteht beispielsweise ebenso wie Graphit aus reinem Kohlenstoff; die Kohlenstoffatome sind allerdings im Diamantkristall anders angeordnet.
- Salze bestehen aus positiv und negativ geladenen Ionen. Die starken Bindungskräfte des Ionengitters haben eine große Härte und Festigkeit der Salzkristalle zur Folge.
- In Metallen sind die einzelnen Kristalle mikroskopisch klein und unregelmäßig angeordnet; sie sind jedoch bei mikroskopischer Betrachtung der Bruchflächen eines Metallstücks deutlich erkennbar.
Bei polykristallinen Materialien, wie beispielsweise Metallen, sind die Größen und Strukturen der einzelnen Teilkristalle unterschiedlich; das Material im Ganzen besitzt daher üblicherweise in alle Raumrichtungen gleiche Eigenschaften. Im Vergleich dazu bestehen monokristalline Stoffe aus einer einzelnen Kristallstruktur, so dass sich die mechanischen, thermischen und elektrischen Eigenschaften in den verschiedenen Raumrichtungen unterscheiden.
Für alle Festkörper mit kristalliner Struktur gilt, dass sie bei einer ganz bestimmten Temperatur (der „Schmelztemperatur“) in den flüssigen Aggregatzustand übergehen. Bei manchen Stoffen, die umgangssprachlich ebenfalls als feste Stoffe bezeichnet werden, ist eine strikte Trennung zwischen festem und flüssigem Aggregatzustand nicht möglich. Diese Materialien – beispielsweise Glas, Wachs, Teer und viele Kunststoffe – haben keinen kristallinen Aufbau und werden daher als „amorphe“ Stoffe bezeichnet.[1]
Dehnung und Stauchung¶
In Festkörpern sind die Abstände zwischen den einzelnen Atomen sehr gering; sie haben daher ein bestimmtes Volumen und lassen sich kaum komprimieren. Allerdings lässt sich die Gestalt eines Festkörpers ändern, beispielsweise kann ein Metalldraht unter Verwendung durch Einwirken einer Zugkraft gedehnt werden. Ob die Gestalt des Festkörpers in ihre alte Form zurück geht, wenn die einwirkende Kraft nachlässt („elastische Verformung“) oder ob sie bestehen bleibt („plastische Verformung“), ist vom Material und der Größe der verformenden Kraft abhängig.[2]
Dehnung von Festkörpern
Im Allgemeinen kann jeder Festkörper zu einem gewissen Grad elastisch gedehnt
werden; dabei vergrößert sich seine Länge  um ein bestimmtes Stück
um ein bestimmtes Stück
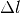 . Wird der Festkörper weiter gedehnt, so bildet sich die
Verformung bei einem Nachlassen der Zugkraft nur noch teilweise oder sogar
überhaupt nicht mehr zurück; die Verformung bleibt also bestehen („plastische
Verformung“).
. Wird der Festkörper weiter gedehnt, so bildet sich die
Verformung bei einem Nachlassen der Zugkraft nur noch teilweise oder sogar
überhaupt nicht mehr zurück; die Verformung bleibt also bestehen („plastische
Verformung“).
Im elastischen Bereich ist die relative Längenänderung 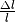 häufig proportional zur einwirkende Kraft
häufig proportional zur einwirkende Kraft  . In diesem Fall kann
das Hookesche Gesetz in einer allgemeinen Form
dargestellt werden:
. In diesem Fall kann
das Hookesche Gesetz in einer allgemeinen Form
dargestellt werden:
Formel:
Eine elastische Dehnung
ist proportional zur einwirkenden Zugspannung
:
(1)¶
Hierbei bezeichnet
die Größe der (senkrecht) einwirkenden Kraft und
die Fläche, auf welche die Kraft einwirkt. Der Proportionalitätsfaktor
wird als „Elastizitätsmodul“ bezeichnet und ist eine Materialkonstante. Die Zugspannung
sowie das Elastizitätsmodul
werden in der Einheit Pascal angegeben.[3]
Stellt man die von der Dehnung 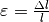 abhängige Zugspannung
abhängige Zugspannung  in einem Diagramm dar, so verläuft die
Kurve im Hookeschen Bereich linear. Die Steigung dieser Kurve ist
in einem Diagramm dar, so verläuft die
Kurve im Hookeschen Bereich linear. Die Steigung dieser Kurve ist
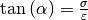 , was nach Gleichung
(1) gerade dem Elastizitätsmodul
, was nach Gleichung
(1) gerade dem Elastizitätsmodul 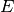 entspricht.
entspricht.

Diagramm der Dehnung eines metallischen Festkörpers in Abhängigigkeit von der einwirkenden Zugspannung.
In der Praxis wird die Grenze des elastischen Bereichs üblicherweise bestimmt,
indem geprüft wird, ab welcher Zugspannung eine 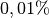 -ige Dehnung
bestehen bleibt. Viele Materialien, beispielsweise Metalldrähte, beginnen
schließlich bei einer ausreichend großen Krafteinwirkung zu „fließen“, bis sie
bei der so genannten Bruchspannung zerreißen. Spröde Materialien wie Glas
hingegen brechen bereits nach Überschreiten ihrer Elastizitätsgrenze.
-ige Dehnung
bestehen bleibt. Viele Materialien, beispielsweise Metalldrähte, beginnen
schließlich bei einer ausreichend großen Krafteinwirkung zu „fließen“, bis sie
bei der so genannten Bruchspannung zerreißen. Spröde Materialien wie Glas
hingegen brechen bereits nach Überschreiten ihrer Elastizitätsgrenze.
| Material | Elastizitätsmodul in 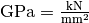 |
| Aluminium | 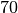 bis bis 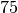 |
| Beton | 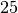 |
| Diamant | 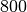 |
| Eisen | 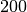 |
| Gusseisen | 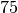 |
| Glas | 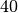 bis bis 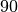 |
| Gummi | 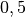 |
| Holz | 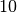 bis bis 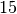 |
| Knochen | 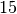 |
| Kupfer | 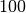 bis bis 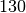 |
| Stahl | 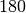 bis bis 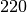 |
| Ziegel | 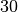 |
Wird ein Zugversuch sehr schnell durchgeführt, die Belastung also eher
schlagartig erfolgt, so zeigt die Kurve im 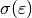 -Diagramm
sich oftmals erhebliche Abweichungen. Auch die Temperatur hat einen Einfluss auf
die Elastizität eines Materials: Beispielsweise ähneln die Eigenschaften eines
weichen Stahl unter tiefen Temperaturen denen eines härteren Stahls.
Üblicherweise wird der Elastizitätsmodul daher durch langsame Zugversuche bei
-Diagramm
sich oftmals erhebliche Abweichungen. Auch die Temperatur hat einen Einfluss auf
die Elastizität eines Materials: Beispielsweise ähneln die Eigenschaften eines
weichen Stahl unter tiefen Temperaturen denen eines härteren Stahls.
Üblicherweise wird der Elastizitätsmodul daher durch langsame Zugversuche bei
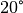 ermittelt.
ermittelt.
Querkontraktion
Mikroskopisch betrachtet sind die Veränderungen der Kristallstruktur bei einer Dehnung meist kompliziert; die Gitterstruktur von Festkörpern ist nicht perfekt, sondern weist immer einige Fehl- und Leerstellen auf. Diese Leerstellen können bei Krafteinwirkungen von benachbarten Gitteratomen aufgefüllt werden, wodurch anderer Stelle neue Lücken entstehen. Aus makroskopischer Sicht kann man bei einer Dehnung mit der Längenzunahme in den meisten Fällen auch eine Verringerung des Querschnitts feststellen; das Volumen des Festkörpers nimmt dabei geringfügig zu.
Diese so genannte Querkontraktion kann mittels der Querkontraktionszahl
(„Poisson-Zahl“) 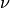 beschrieben werden, welche das Verhältnis der
Längenänderung in Querrichtung
beschrieben werden, welche das Verhältnis der
Längenänderung in Querrichtung 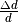 im Verhältnis zur
Längenänderung in Zugrichtung
im Verhältnis zur
Längenänderung in Zugrichtung 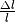 angibt:
angibt:
(2)¶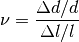
Die Querkontraktionszahl ist dimensionslos. Für die Volumenänderung bei einer Zugspannung in Längsrichtung gilt damit näherungsweise:
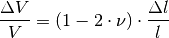
Die Werte der Querkontraktionszahl 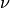 liegen üblicherweise zwischen
liegen üblicherweise zwischen
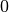 und
und 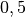 . Ist
. Ist 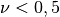 , so nimmt bei einer wirkenden
Zugspannung das Volumen zu, denn in diesem Fall ist
, so nimmt bei einer wirkenden
Zugspannung das Volumen zu, denn in diesem Fall ist 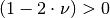 ,
und
,
und 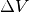 sowie
sowie 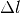 haben das gleiche Vorzeichen. Im
Fall
haben das gleiche Vorzeichen. Im
Fall 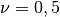 bleibt das Volumen bei einer Zugspannung unverändert.
bleibt das Volumen bei einer Zugspannung unverändert.
| Material | Querkontraktionszahl 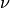 |
| Aluminium | 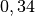 |
| Beton | 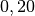 |
| Glas | 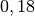 bis bis 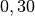 |
| Gummi | 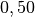 |
| Holz | 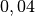 bis bis 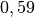 |
| Kupfer | 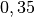 |
| Schaumstoff | 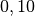 bis bis 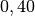 |
| Stahl | 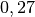 bis bis 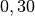 |
Bei manchen Materialien, beispielsweise bei Holz, sind die Werte des
Elastizitätsmoduls 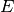 sowie der Querkontraktionszahl
sowie der Querkontraktionszahl 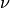 davon
abhängig, ob die Zugspannung in Faserrichtung oder quer zur Faserrichtung
wirkt. Bei Werten von
davon
abhängig, ob die Zugspannung in Faserrichtung oder quer zur Faserrichtung
wirkt. Bei Werten von 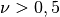 tritt bei einer Zugspannung eine Abnahme
des Volumens auf; dies ist bei diversen porösen Materialien der Fall.
tritt bei einer Zugspannung eine Abnahme
des Volumens auf; dies ist bei diversen porösen Materialien der Fall.
Stauchung von Festkörpern
Bei einer Stauchung wirken Kräfte senkrecht auf die Oberflächen eines Körpers ein. Dabei verkürzt sich die Länge des Materials, auf die der Druck einwirkt; bei ausreichend großen Drücken lässt sich auch eine geringfügige Abnahme des Volumens feststellen. Der Probekörper kann sich bei einer Stauchung – je nach Form und Festigkeit – auch verbiegen oder umknicken, wenn die maximale Belastbarkeit überschritten wird. Typische Beispiele für Stauchungen sind das Zusammenpressen einer Schuhsohle oder eines Brückenpfeilers unter der einwirkenden Gewichtskraft.
Auch bei einer Stauchung wird die Formänderung des Materials durch eine
(Druck-)Spannung beschrieben. Die Druckspannung ist ebenso wie die Zugspannung
definiert als Verhältnis der einwirkenden Kraft  zur Querschnittsfläche
zur Querschnittsfläche
 des Materials. Das Symbol für die stauchende Spannung ist wiederum
des Materials. Das Symbol für die stauchende Spannung ist wiederum
 , die Einheit ist ebenfalls Pascal. Für eine elastische Stauchung
gilt:
, die Einheit ist ebenfalls Pascal. Für eine elastische Stauchung
gilt:
(3)¶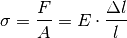
Die Druckspannung entspricht formal der Zugspannung, hat jedoch aufgrund der
entgegengesetzten Richtung der Kraft ein negatives Vorzeichen; ebenso ist in
diesem Fall die „Stauchung“ 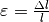 negativ.
In einem Spannungs-Dehnungs-Diagramm verläuft die Kurve einer Stauchung somit
im dritten Quadranten.
negativ.
In einem Spannungs-Dehnungs-Diagramm verläuft die Kurve einer Stauchung somit
im dritten Quadranten.
Bei einer elastischen Stauchung ist der Proportionalitätsfaktor 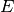 im
Hookeschen Bereich mit dem Elastizitätsmodul
im
Hookeschen Bereich mit dem Elastizitätsmodul
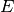 einer elastischen Dehnung identisch. Bei stärkeren Belastungen weicht
die Form der Stauchungs-Kurve meist deutlich von der Dehnungs-Kurve ab. Bei
manchen Materialien, beispielsweise Stein, Beton, Keramik oder Gusseisen sind
die maximalen Belastungen gegenüber Druckspannungen zudem wesentlich größer als
die gegenüber Zugspannungen.
einer elastischen Dehnung identisch. Bei stärkeren Belastungen weicht
die Form der Stauchungs-Kurve meist deutlich von der Dehnungs-Kurve ab. Bei
manchen Materialien, beispielsweise Stein, Beton, Keramik oder Gusseisen sind
die maximalen Belastungen gegenüber Druckspannungen zudem wesentlich größer als
die gegenüber Zugspannungen.
Biegung
Eine Biegung, beispielsweise eines Balkens, entsteht durch eine Krafteinwirkung
auf das eine Ende des Gegenstands, während das andere Ende fest eingespannt ist.
Das Produkt aus der Länge  des Gegenstands und der Kraft
des Gegenstands und der Kraft  entspricht dem wirkenden Drehmoment
entspricht dem wirkenden Drehmoment 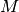 .
.
Kennzeichnend für eine Biegung ist eine „neutrale Faser“ in der Mitte des Gegenstands. Oberhalb dieser neutralen Faser steht der Gegenstand unter Zugspannung und wird gedehnt, unterhalb der neutralen Faser steht der Gegenstand unter Druckspannung und wird gestaucht.
Auf Höhe der neutralen Faser wechselt die Spannung und Dehnung das Vorzeichen von positiv (Zugspannung) zu negativ (Druckspannung). Wird die Elastizitätsgrenze des Materials auf der Zug- oder Druckseite überschritten, so geht die Biegung in eine Knickung über.
Scherung und Torsion¶
Bei Scherungen und Torsionen werden parallel zueinander liegende Oberflächen gegeneinander verschoben oder verdreht. Die Länge des Gegenstands sowie sein Querschnitt bleiben dabei unverändert.
Scherung von Festkörpern
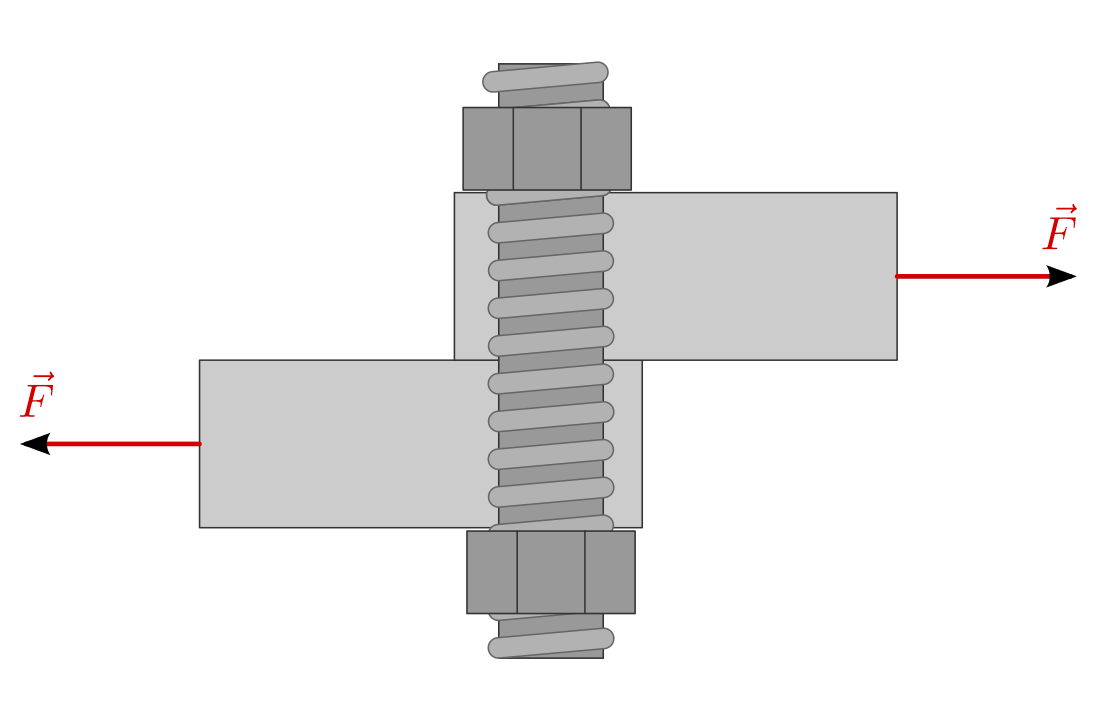
Bei einer Scherung wird durch Krafteinwirkung eine Seite eines Materials gegenüber einer gegenüber liegenden Seite verschoben; die scherenden Kräfte wirken dabei stets tangential zur Materialoberfläche. Eine scherende Kraft kann ein Material biegen, verschieben oder verdrehen. Ein typisches Beispiel für Scherungs-Beanspruchungen sind Kräfte, die auf Schrauben in Regalträgern einwirken. Ebenso können Zugkräfte auf Platten, die durch Nieten zusammengehalten werden, Scherspannungen hervorrufen. Auch die Schneidekanten von Scheren bewirken Scherungen im zu zerschneidenden Material.
Das Symbol für die Scherspannung ist 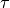 , die Einheit ebenfalls Pascal.
Die Scherspannung ist wiederum definiert als Verhältnis der einwirkenden Kraft
, die Einheit ebenfalls Pascal.
Die Scherspannung ist wiederum definiert als Verhältnis der einwirkenden Kraft
 zur Querschnittsfläche
zur Querschnittsfläche  des Materials. Für eine elastische
Scherung gilt:
des Materials. Für eine elastische
Scherung gilt:
(4)¶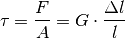
Der Proportionalitätsfaktor 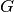 wird Gleit- oder Schubmodul genannt und
ist eine Materialkonstante. Die Einheit von
wird Gleit- oder Schubmodul genannt und
ist eine Materialkonstante. Die Einheit von 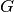 ist wiederum Pascal; je
größer der Wert des Schubmodul eines Materials ist, desto größer ist seine auch
Steifigkeit. Allgemein ist der Schubmodul eines Materials kleiner als der
Elastizitätsmodul, es gilt also
ist wiederum Pascal; je
größer der Wert des Schubmodul eines Materials ist, desto größer ist seine auch
Steifigkeit. Allgemein ist der Schubmodul eines Materials kleiner als der
Elastizitätsmodul, es gilt also 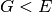 ; bei vielen Metallen beträgt der
Schubmodul etwa ein Drittel ihres Elastizitätsmoduls. Scherspannungen führen
somit schneller zu Brüchen als gleich große Zug- oder Druckspannungen.
; bei vielen Metallen beträgt der
Schubmodul etwa ein Drittel ihres Elastizitätsmoduls. Scherspannungen führen
somit schneller zu Brüchen als gleich große Zug- oder Druckspannungen.
Die Scherung 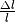 kann auch durch den Scherwinkel
kann auch durch den Scherwinkel
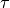 ausgedrückt werden, denn es gilt:
ausgedrückt werden, denn es gilt:
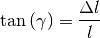
Ist der Scherwinkel klein 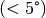 , so kann näherungsweise
, so kann näherungsweise
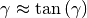 gesetzt werden.
gesetzt werden.
Torsion von Festkörpern
Als Torsion wird eine Verdrillung eines Körpers, beispielsweise eines
zylindrischen Stabes, bezeichnet. Bei dieser Art von Deformation handelt es sich
prinzipiell ebenfalls um eine Scherung.
Auch bei Torsionen gibt es einen elastischen Bereich, in dem die Verdrillung
proportional zur Schubspannung 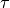 ist. Für eine elastische Torsion
eines Stabes mit Radius
ist. Für eine elastische Torsion
eines Stabes mit Radius  gilt:
gilt:
(5)¶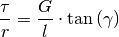
Hierbei bezeichnet  die Länge des Stabs und
die Länge des Stabs und 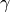 den
Torsionswinkel. Der Proportionalitätsfaktor
den
Torsionswinkel. Der Proportionalitätsfaktor 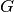 steht wiederum für der
Schubmodul des Materials.
steht wiederum für der
Schubmodul des Materials.
Kompression¶
Wird auf einen Körper zunehmend ein allseitiger Druck ausgeübt, beispielsweise
durch den hydrostatischen Druck in einer
Flüssigkeit, so verkleinert sich entsprechend sein Volumen. Der Zusammenhang
zwischen der auftretenden Druckänderung 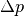 und der resultierenden
relativen Volumenänderung
und der resultierenden
relativen Volumenänderung 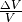 kann mittels des so
genannten Kompressionsmoduls
kann mittels des so
genannten Kompressionsmoduls 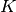 beschrieben werden:
beschrieben werden:
(6)¶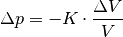
Die Einheit des Kompressionsmoduls 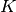 ist Pascal, wie auch die Einheit
des Drucks. Das negative Vorzeichen in der obigen Gleichung ergibt sich daraus,
dass bei einem von außen einwirkenden, positiven Druck das Volumen kleiner wird,
also in diesem Fall
ist Pascal, wie auch die Einheit
des Drucks. Das negative Vorzeichen in der obigen Gleichung ergibt sich daraus,
dass bei einem von außen einwirkenden, positiven Druck das Volumen kleiner wird,
also in diesem Fall 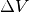 negativ ist.
negativ ist.
Eine Abnahme des Volumens  bei einer Kompression ist gleichbedeutend
mit einer Zunahme der Dichte
bei einer Kompression ist gleichbedeutend
mit einer Zunahme der Dichte 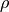 des Gegenstands. Dies kann man
folgendermaßen herleiten:
des Gegenstands. Dies kann man
folgendermaßen herleiten:
Die Masse
 des Objekts ändert sich während der Kompression nicht.
Somit ist die Änderung
des Objekts ändert sich während der Kompression nicht.
Somit ist die Änderung 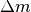 gleich Null:
gleich Null: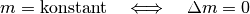
Für die Masse kann man
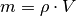 schreiben. Für die zeitliche
Änderung der Masse ergibt sich nach der Produktregel:
schreiben. Für die zeitliche
Änderung der Masse ergibt sich nach der Produktregel:
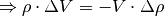
Die obige Gleichung kann folgendermaßen umgestellt werden:
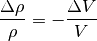
Man kann für die obige Gleichung (6) folglich auch schreiben:
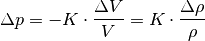
Während also das Volumen bei einer Kompression abnimmt (negatives Vorzeichen), nimmt die Dichte zu.
Je größer der Wert des Kompressionsmoduls 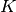 ist, desto größer ist der
nötige Druck, um eine bestimmte relative Volumenänderung zu erreichen. Die Werte
von
ist, desto größer ist der
nötige Druck, um eine bestimmte relative Volumenänderung zu erreichen. Die Werte
von 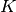 von Festkörpern und Flüssigkeiten sind üblicherweise um mehrere
Größenordnungen höher als die von Gasen.
von Festkörpern und Flüssigkeiten sind üblicherweise um mehrere
Größenordnungen höher als die von Gasen.
| Material | Kompressionsmodul 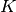 in in 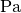 |
| Diamant | 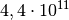 |
| Glas | 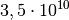 bis bis 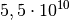 |
| Luft | 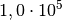 (isotherm) bis (isotherm) bis 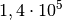 (adiabatisch) (adiabatisch) |
| Öl | 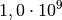 bis bis 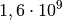 |
| Stahl | 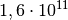 |
| Wasser | 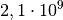 |
Ist der Kompressionsmodul eines Materials hoch, so bedeutet dies, dass das
Material einer Kompression einen hohen Widerstand entgegensetzt, sich also nur
schwer komprimieren lässt. Beispielsweise bei Gasen wird hingegen häufig der
Kehrwert des Kompressionsmoduls , die so genannte Kompressibilität 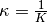 verwendet. Ein Material mit einer hohen Kompressibilität
verwendet. Ein Material mit einer hohen Kompressibilität
 ist also leicht zu komprimieren.
ist also leicht zu komprimieren.
Anmerkungen:
| [1] | Ist der Elastizitätsmodul eines Materials hoch, so sagt man, dass das
Material eine hohe „Steifigkeit“ besitzt. Diese ist formal definiert als
Verhältnis der aufzubringenden Kraft
Zwischen dem Elastizitätsmodul
Die Steifigkeit hängt somit nicht nur vom Material eines Gegenstands, sondern auch von seiner Form ab. |
| [2] | Streng genommen handelt es sich bei amorphen Stoffen um Flüssigkeiten mit einer sehr hohen inneren Reibung („Viskosität“). |
| [3] | Neben den elastischen und plastischen Verformungen sind auch so genannte viskoelastische Verformungen möglich, bei denen die elastische Verformung mit einer gewissen zeitlichen Verzögerung eintritt. In diesem Fall bildet sich die Verformung beim Nachlassen der Kraft erst nach einer gewissen Zeit zurück. Beispiele für solche viskoelastischen Stoffe sind hochpolymere Kunststoffe und die menschliche Haut. |
Hinweis
Zu diesem Abschnitt gibt es Übungsaufgaben.