Mechanik der Flüssigkeiten¶
In der Hydrodynamik werden die mechanischen Eigenschaften von Flüssigkeiten, insbesondere von Wasser, untersucht.
Druck in Flüssigkeiten¶
Flüssigkeiten lassen sich durch mechanische Belastung (fast) nicht zusammenpressen („komprimieren“). Dies gilt sowohl für von außen wirkende Kräfte wie auch für den so genannten „Schweredruck“, der sich aus dem Eigengewicht der Flüssigkeit ergibt.
Kolbendruck
Übt man mit einem Kolben eine Kraft auf eine Flüssigkeit aus, die sich in einem geschlossenen Behälter befindet, so bleibt das Volumen der Flüssigkeit unverändert; allerdings baut sich im Inneren der Flüssigkeit ein „Gegendruck“ auf, der die von außen einwirkende Kraft ausgleicht.
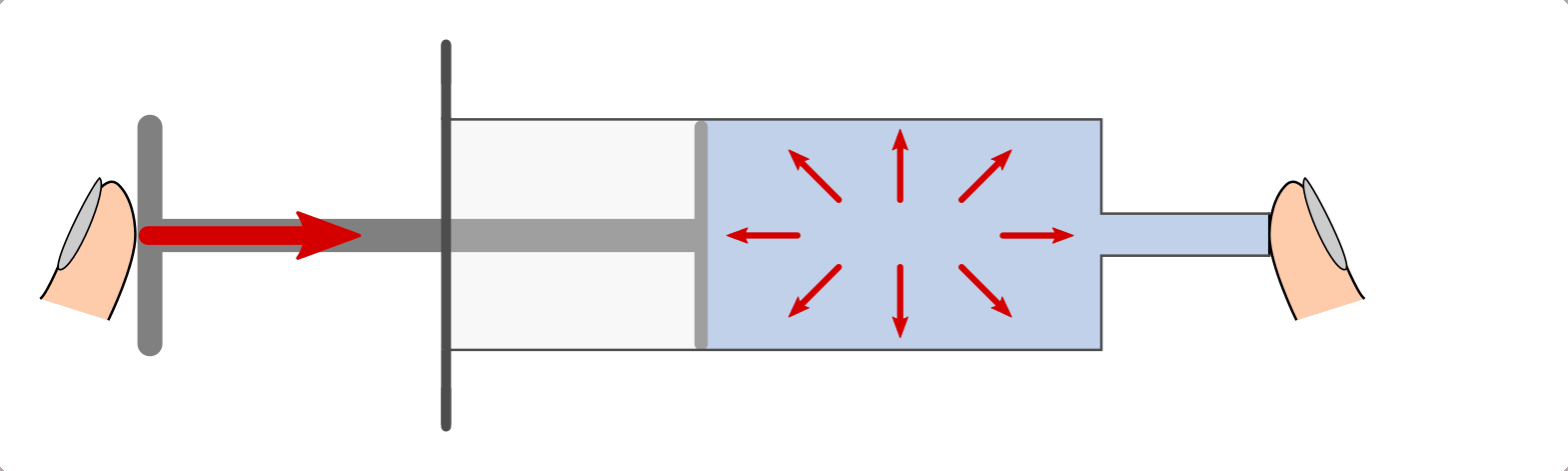
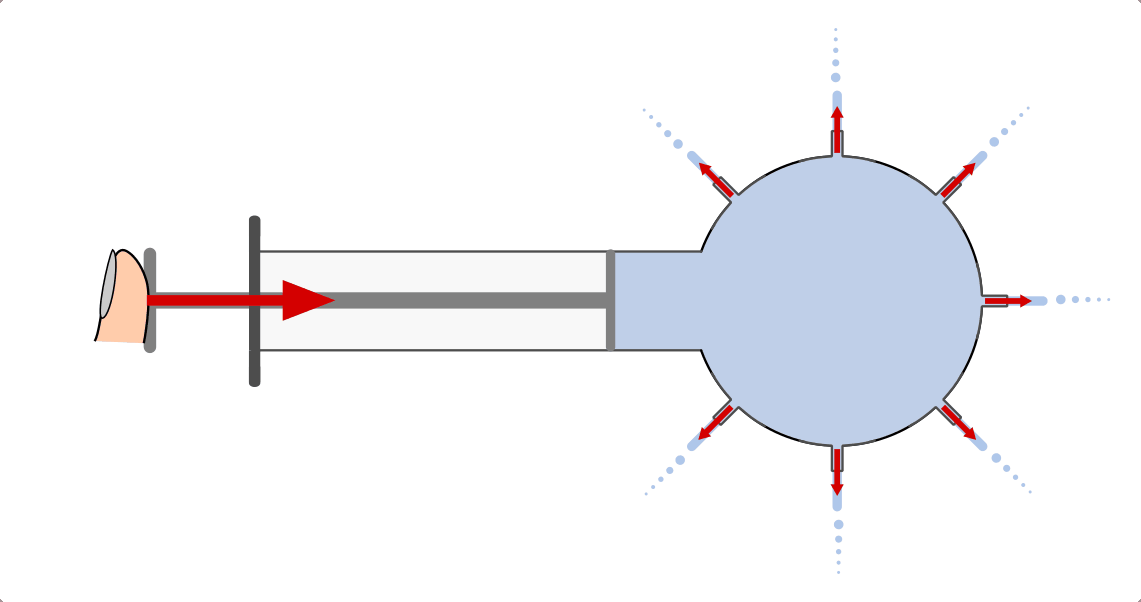
In einer Flüssigkeit oder in einem Gas wirkt der Kolbendruck stets in alle Raumrichtungen gleich stark („Pascalsches Prinzip“). Wird beispielsweise von links Druck auf Wasser ausgeübt, das sich in einem durchlöcherten Schlauch oder einem so genannten „Druckfortpflanzungs-Apparat“ befindet, so tritt das Wasser an den allen Öffnungen senkrecht zur Oberfläche aus.[1]
Definition:
Einheit:
Die Grundeinheit des Drucks, die sich aus der obigen Formel ergibt, ist nach Blaise Pascal benannt. Für ein Pascal
gilt folgender Zusammenhang:
Größere Drücke, wie sie in der alltäglichen Praxis des öfteren anzutreffen sind, werden häufig in der Einheit „Bar“
angegeben. Dabei gilt:
Ein Bar entspricht auf der Erde in etwa der Größe des Luftdrucks in Bodennähe.
Der gegebenenfalls auf ein Fluid einwirkende Kolbendruck sowie der im nächsten
Abschnitt behandelte Schweredruck werden in Summe auch als statischer Druck
 bezeichnet. Diese Druckformen treten sowohl in
ruhenden wie auch in sich bewegenden Fluiden auf und wirken an einer gegebenen
Stelle stets in alle Raumrichtungen gleichermaßen.
bezeichnet. Diese Druckformen treten sowohl in
ruhenden wie auch in sich bewegenden Fluiden auf und wirken an einer gegebenen
Stelle stets in alle Raumrichtungen gleichermaßen.
Schweredruck
Durch das Eigengewicht der Flüssigkeit wird innerhalb der Flüssigkeit ein mit zunehmender Tiefe immer größer werdender Schweredruck hervorgerufen; dieser wirkt in einer bestimmten Tiefe in alle Raumrichtungen gleich stark.
Die Größe 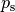 des Schweredrucks lässt sich berechnen, wenn man
das Volumen einer Flüssigkeitssäule mit einer Grundfläche
des Schweredrucks lässt sich berechnen, wenn man
das Volumen einer Flüssigkeitssäule mit einer Grundfläche  und einer
Gewichtskraft
und einer
Gewichtskraft 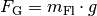 betrachtet.
betrachtet.
Am Boden der Flüssigkeitssäule gilt:
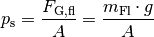
Die Masse  der Flüssigkeit kann auch als Produkt aus ihrer Dichte
der Flüssigkeit kann auch als Produkt aus ihrer Dichte 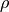 und ihrem Volumen
und ihrem Volumen  geschrieben werden. Das
Volumen
geschrieben werden. Das
Volumen  der Flüssigkeit wiederum entspricht dem Produkt aus der
Grundfläche
der Flüssigkeit wiederum entspricht dem Produkt aus der
Grundfläche  und der Höhe
und der Höhe 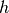 des betrachteten Quaders. Es
gilt also:
des betrachteten Quaders. Es
gilt also:
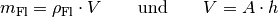
Setzt man 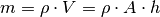 in die obere
Gleichung ein, so kann die Fläche
in die obere
Gleichung ein, so kann die Fläche  im Zähler und Nenner gekürzt
werden. Es ergibt sich damit folgende Formel:
im Zähler und Nenner gekürzt
werden. Es ergibt sich damit folgende Formel:
(2)¶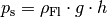
Der Schweredruck in einer Flüssigkeit hängt, da der Ortsfaktor 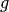 konstant ist, nur von der Dichte der Flüssigkeit und der Höhe der
Flüssigkeitssäule ab.
konstant ist, nur von der Dichte der Flüssigkeit und der Höhe der
Flüssigkeitssäule ab.
Beispiel:
Wie hoch ist der Schweredruck des Wassers in
![h=\unit[10]{m}](../../_images/math/03ecf0389944e9eeb526b0a2360fb1b7361e9bfb.png) unterhalb
der Wasseroberfläche?
unterhalb
der Wasseroberfläche?Für den Schweredruck gilt mit
![\rho_{\mathrm{Wasser}} =
\unit[1000]{\frac{kg}{m^3}}](../../_images/math/6e93b2c40a2e79feedeaa48be475e8ffcfc904e4.png) :
:![p_{\mathrm{s}} = \rho \cdot g \cdot h = \unit[1000]{\frac{kg}{m^3}} \cdot
\unit[9,81]{\frac{N}{kg}} \cdot \unit[10]{m} = \unit[98\,100]{Pa}](../../_images/math/dc1e38973ea90a0c692c401c5ef150dbbc3434e8.png)
Der Schweredruck des Wassers in
![h=\unit[10]{m}](../../_images/math/03ecf0389944e9eeb526b0a2360fb1b7361e9bfb.png) beträgt somit knapp
beträgt somit knapp
![\unit[100\,000]{Pa}](../../_images/math/71d86ff9f017f36d28b93e2fb50ab326c9a38a61.png) , also rund
, also rund ![\unit[1]{bar}](../../_images/math/6e104f5aba80ffafeaa668badd6fbfaa9bf2a2be.png) .
.
Um Verwechslungen zu vermeiden, wird die Angabe des Schweredrucks in einer
Flüssigkeit häufig um die Angabe 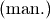 ergänzt. Dieses Kürzel
steht für „Manometer-Druck“ und soll darauf hindeuten, dass sich die Druckangabe
relativ zum Luftdruck bezieht. Addiert man beispielsweise zu dem Schweredruck
von
ergänzt. Dieses Kürzel
steht für „Manometer-Druck“ und soll darauf hindeuten, dass sich die Druckangabe
relativ zum Luftdruck bezieht. Addiert man beispielsweise zu dem Schweredruck
von ![p_{\mathrm{s}}=\unit[1]{bar} \text{ (man.)}](../../_images/math/eff8d18d0d6e7a8edc31771a1234f8129225e1dc.png) noch den Luftdruck dazu,
der ebenfalls
noch den Luftdruck dazu,
der ebenfalls ![p_{\mathrm{Luft}} = \unit[1]{bar}](../../_images/math/cee8f1a43fa1a1b1eaacb597c5e64004ff9d3815.png) groß ist, so erhält man
groß ist, so erhält man
![p = \unit[2]{bar} \text{ (abs.)}](../../_images/math/40a9d43f73bd6957453c5bbd4936d2258a05f4c3.png) als „absoluten“ Druck, der in dieser
Tiefe vorherrscht.
als „absoluten“ Druck, der in dieser
Tiefe vorherrscht.
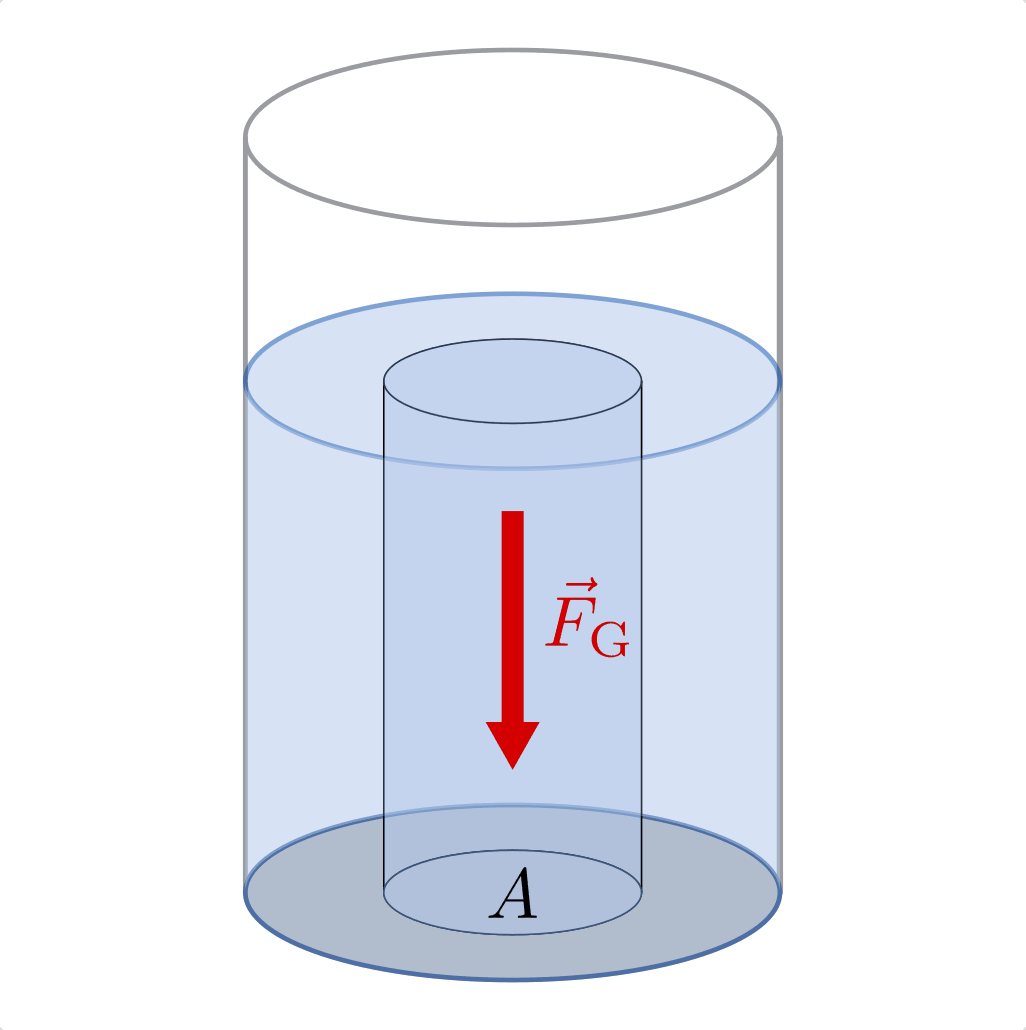
Die Zunahme des Schweredrucks mit der Tiefe ist unabhängig von der Form der darüber liegenden Wassersäule. Dieses als „hydrostatisches Paradoxon“ bekannte Prinzip kann man beispielsweise mittels einer Anordnung von unterschiedlich geformten Glasgefäßen zeigen, die untereinander durch Wasserleitungen verbunden sind („kommunizierende Gefäße“). Bei einer solchen Anordnung ist das Wasserniveau in allen Gefäßen gleich hoch – ein höheres Wasserniveau in einem der Gefäße hätte einen höheren Wasserdruck auf die unteren Wasserschichten in diesem Gefäß zur Folge, wodurch wiederum Wasser von dort in die übrigen Gefäße gepresst würde. Dieses Prinzip wird nicht nur zur Konstruktion von Siphons als „Geruchstopper“ verwendet (beispielsweise an Waschbecken), sondern ebenso, um mittels so genannter „Schlauchwaagen“ – ähnlich wie mit Wasserwaagen – über sehr große Entfernungen hinweg eine waagrechte Ausrichtung von Gegenständen zu erreichen.
Druckmessung¶
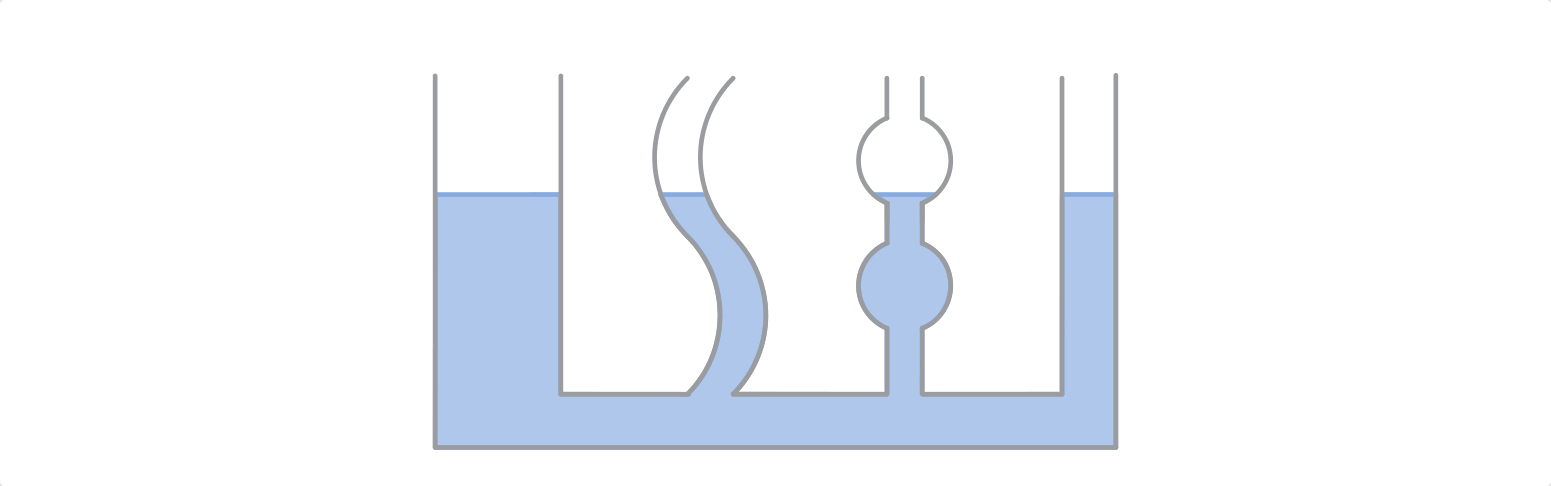
Die Zunahme des Schweredrucks mit der Höhe der Wassersäule wird bei so genannten
„U-Rohr-Manometern“ zur Druckmessung genutzt. Als „Manometer“ bezeichnet man
allgemein Druckmessgeräte, die einen externen, relativ zum Luftdruck
vorherrschenden Druck 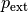 messen.
messen.
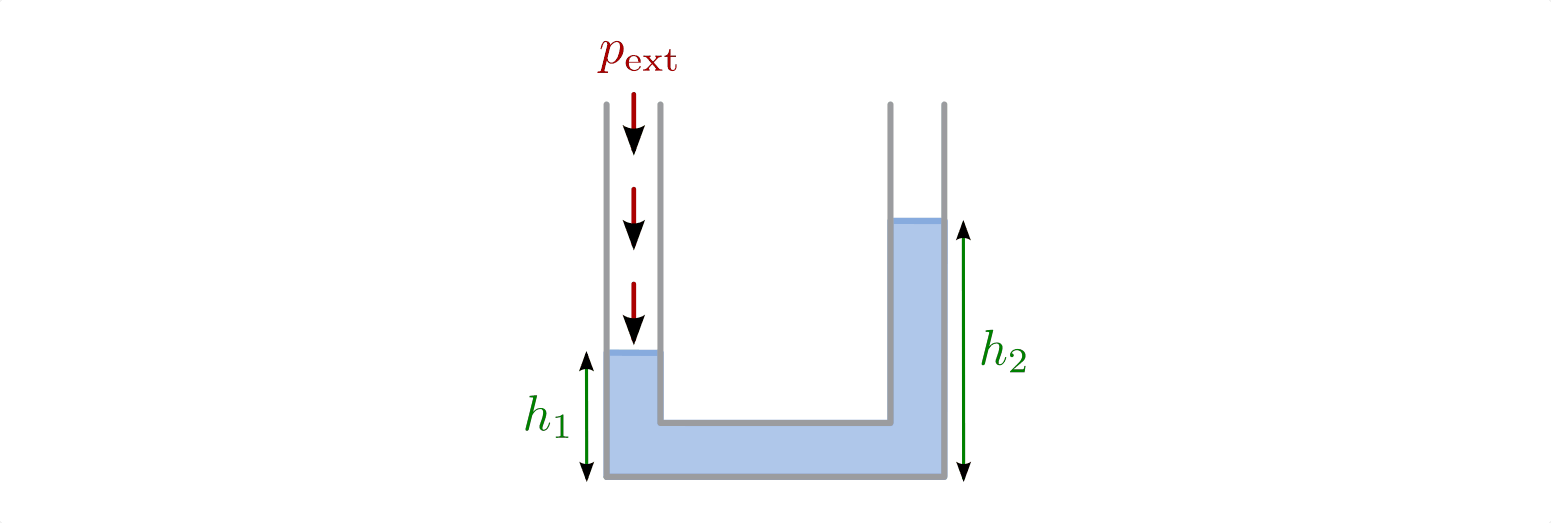
Wird auf ein Ende eines mit einer Flüssigkeit gefüllten U-Rohrs ein externer Druck
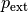 ausgeübt, so wird durch diesen die Flüssigkeit in die
andere Hälfte des U-Rohrs verdrängt. Dies erfolgt so lange, bis sich in der
anderen Hälfte durch die höhere Wassersäule ein hinreichend großer Schweredruck
aufgebaut hat, der dem externen Druck
ausgeübt, so wird durch diesen die Flüssigkeit in die
andere Hälfte des U-Rohrs verdrängt. Dies erfolgt so lange, bis sich in der
anderen Hälfte durch die höhere Wassersäule ein hinreichend großer Schweredruck
aufgebaut hat, der dem externen Druck 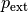 entgegenwirkt.
entgegenwirkt.
Im Gleichgewichtsfall gilt:
(3)¶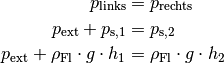
Durch diesen Zusammenhang kann unmittelbar die gesuchte Größe
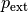 bestimmt werden. Schreibt man
bestimmt werden. Schreibt man 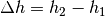 , so folgt:
, so folgt:
(4)¶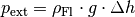
Zur Messung des externen Drucks 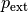 muss somit lediglich
der sich einstellende Unterschied der Füllhöhen, also eine Länge gemessen
werden. Da der Zusammenhang direkt proportional beziehungsweise linear ist, kann
durch eine Kalibrierung auf eine bestimmte Flüssigkeit auch eine entsprechende
Skala mit Druckwerten angebracht werden. Für kleine zu messende Druckwerte
verwendet man eine Flüssigkeit mit geringer Dichte, für hohe Drücke eine
Flüssigkeit mit hoher Dichte, damit ein entsprechend großer Gegendruck durch die
Schwere des Fluids zustande kommt.
muss somit lediglich
der sich einstellende Unterschied der Füllhöhen, also eine Länge gemessen
werden. Da der Zusammenhang direkt proportional beziehungsweise linear ist, kann
durch eine Kalibrierung auf eine bestimmte Flüssigkeit auch eine entsprechende
Skala mit Druckwerten angebracht werden. Für kleine zu messende Druckwerte
verwendet man eine Flüssigkeit mit geringer Dichte, für hohe Drücke eine
Flüssigkeit mit hoher Dichte, damit ein entsprechend großer Gegendruck durch die
Schwere des Fluids zustande kommt.
Genau genommen muss bei der Herleitung des Druck-Gleichgewichts in einem U-Rohr (Gleichung (3)) auch noch der Luftdruck berücksichtigt werden. Dieser wirkt allerdings gleichermaßen auf beide Seiten des U-Rohrs ein und hat daher keinen Einfluss auf das Gleichgewicht. Wäre allerdings das rechte Ende des U-Rohrs oben abgeschlossen und luftleer, so müsste man den dann nur auf die linke Seite einwirkenden Luftdruck berücksichtigen; in diesem Fall spricht man von einem Barometer, das üblicherweise zur Messung des Luftdrucks verwendet wird.
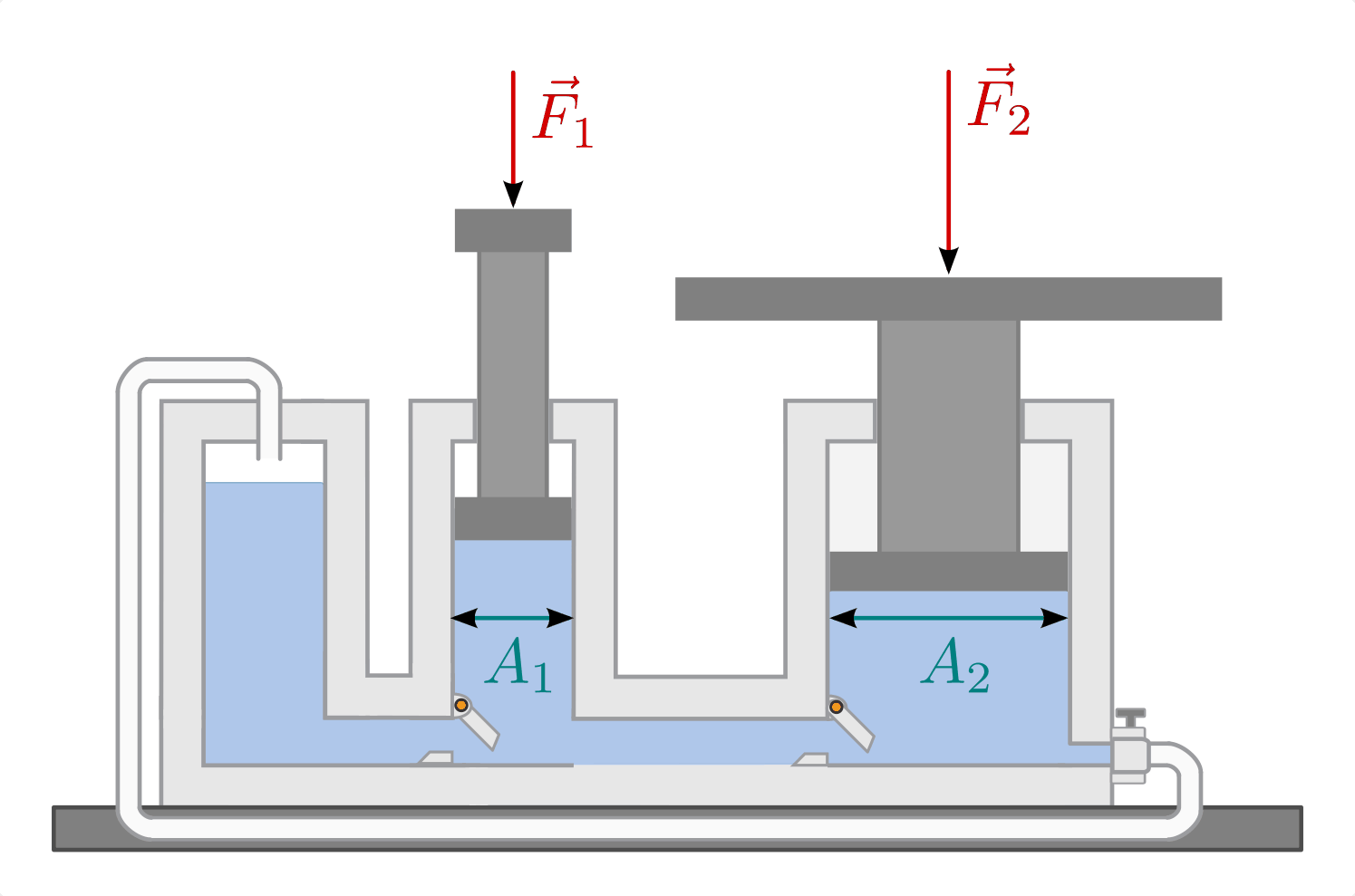
Hydraulische Anlagen und Druckwandler¶
Eine wichtige technische Anwendung der Inkompressibilität und gleichmäßigen
Druckausbreitung in Flüssigkeiten sind hydraulische Anlagen. Hierbei wird auf
der einen Seite eine (verhältnismäßig) schwache Kraft auf einen Kolben mit
möglichst geringem Durchmesser ausgeübt. Der durch den Kolben ausgeübte Druck
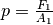 , also das Verhältnis aus der ausgeübten Kraft
, also das Verhältnis aus der ausgeübten Kraft
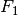 und der Querschnittsfläche
und der Querschnittsfläche 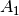 des Kolbens, entspricht in
guter Näherung dem insgesamt in der Flüssigkeit wirkenden Druck, da gegenüber
ihm der Schweredruck meist vernachlässigbar klein ist.
des Kolbens, entspricht in
guter Näherung dem insgesamt in der Flüssigkeit wirkenden Druck, da gegenüber
ihm der Schweredruck meist vernachlässigbar klein ist.
Auf der anderen Seite der hydraulischen Anlage befindet sich ein zweiter Kolben
mit (verhältnismäßig) großer Querschnittsfläche 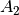 . Da
innerhalb der Flüssigkeit der Kolbendruck
. Da
innerhalb der Flüssigkeit der Kolbendruck 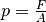 an allen
Stellen gleich groß ist, wird beim Hineinpressen des kleinen Kolbens eine Kraft
auf den großen Kolben ausgeübt, die um das Verhältnis der Kolbenflächen
verstärkt ist:
an allen
Stellen gleich groß ist, wird beim Hineinpressen des kleinen Kolbens eine Kraft
auf den großen Kolben ausgeübt, die um das Verhältnis der Kolbenflächen
verstärkt ist:
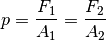
(5)¶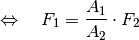
Diese zunächst unerwartete Tatsache, dass eine kleine schwache Kraft auf den kleinen Kolben eine große Kraft am großen Kolben bewirkt, kann man sich anschaulich damit erklären, dass am großen Kolben wesentlich mehr Flüssigkeits-Teilchen „anstoßen“ als am kleinen; die unter Druck gesetzte Flüssigkeit kann daher in Richtung des großen Kolbens auch leichter zusätzlichen Raum einnehmen. Vergleichsweise kann man sich als Merkhilfe auch vorstellen, dass man zum Abdichten eines kleinen Lochs in einer Wasserleitung weniger Kraft braucht als bei einem großen Loch, obwohl der Wasserdruck in beiden Fällen gleich ist.
Eine hydraulische Anlage stellt somit ebenfalls einen Kraftwandler dar. Die goldene Regel der Mechanik gilt unverändert: Um den großen Kolben um eine Höhe
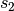 anzuheben, muss man den kleinen Kolben um eine entsprechend längere
Wegstrecke
anzuheben, muss man den kleinen Kolben um eine entsprechend längere
Wegstrecke 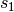 bewegen. Es gilt mit der obigen Gleichung
(5):
bewegen. Es gilt mit der obigen Gleichung
(5):
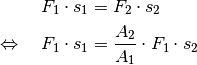
Hierbei kann man die Kraft 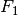 , die als gemeinsamer Faktor auf
beiden Seiten der Gleichung auftritt, kürzen. Für das Verhältnis der
zurückgelegten Wegstrecken folgt damit:
, die als gemeinsamer Faktor auf
beiden Seiten der Gleichung auftritt, kürzen. Für das Verhältnis der
zurückgelegten Wegstrecken folgt damit:
(6)¶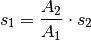
Um den großen Kolben nennenswert nach oben zu bringen, müsste der kleine Kolben wesentlich länger sein. Als Alternative hierzu kann ein Ventil-System und ein Reservoire mit Hydraulik-Flüssigkeit verwendet werden. Während des „Hochpumpens“ der Last wird aus dem Reservoire nachgetankt; zum Herablassen der Last muss hingegen ein Verschluss-Mechanismus geöffnet werden, so dass die Hydraulik-Flüssigkeit durch das Gewicht der Last wieder zurück in das Reservoire gedrückt wird. Hydraulische Anlagen werden in der Praxis unter anderem in Lastenhebern, in Münzpressen sowie in Bremsanlagen von Fahrzeugen eingesetzt.
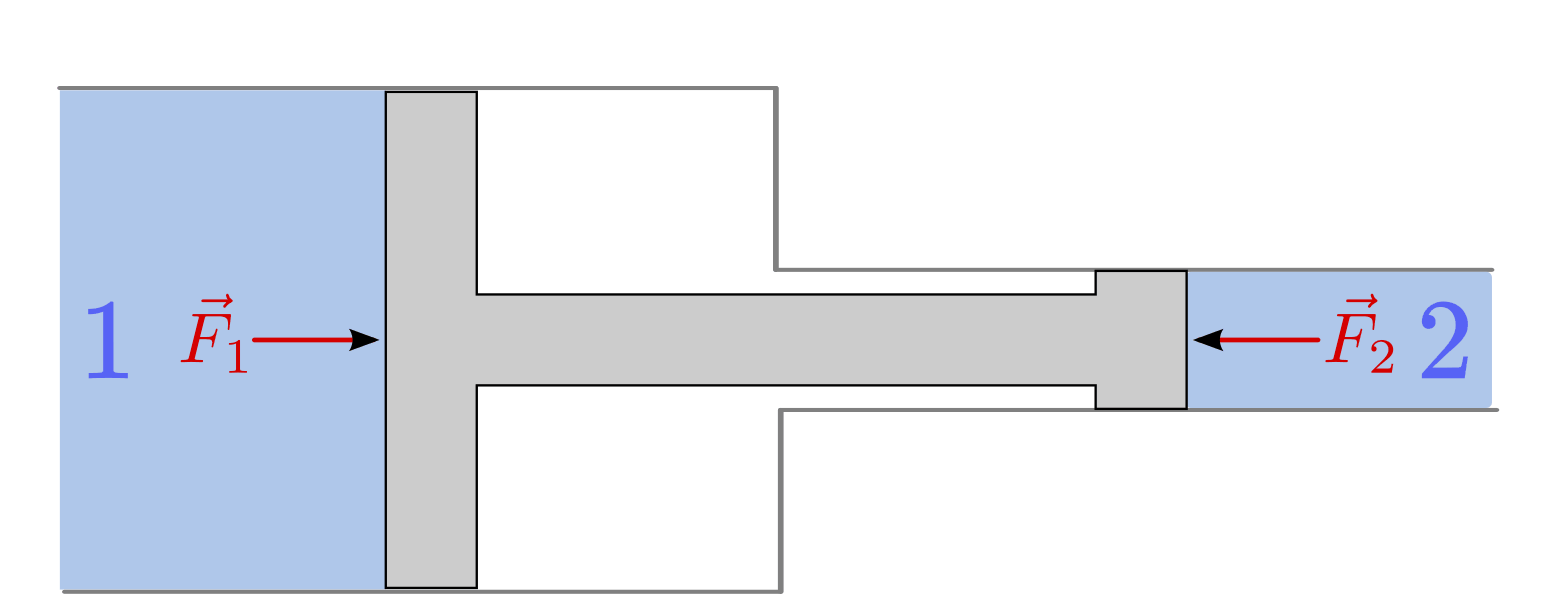
Ein zweites wichtiges Prinzip bei der technischen Verwendung von Fluiden sind so genannte Druckwandler. Diese bestehen im Wesentlichen aus zwei Rohren mit unterschiedlichem Durchmesser und einer sich zwischen den beiden Rohren befindenden Kolbenstange.
Von den beiden Fluiden 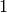 und
und 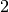 wird jeweils aufgrund der darin
vorherrschenden Drücke eine Kraft auf den Kolben ausgeübt. Im Gleichgewichtsfall
müssen diese beiden Kräfte
wird jeweils aufgrund der darin
vorherrschenden Drücke eine Kraft auf den Kolben ausgeübt. Im Gleichgewichtsfall
müssen diese beiden Kräfte 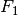 und
und 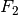 gleich groß sein:
gleich groß sein:
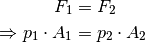
Die in den beiden Fluiden vorherrschenden Drücke sind im Gleichgewichtsfall
somit umgekehrt proportional zu den Querschnittsflächen 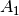 und
und
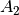 des Kolbens:
des Kolbens:
(7)¶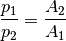
In der praktischen Anwendung wird dieses Prinzip beispielsweise folgendermaßen
verwendet: Auf der linken Seite wird die Druckluft eines Kompressors als Fluid
verwendet; der Druck 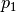 liegt dabei bei etwa
liegt dabei bei etwa ![\unit[10]{bar}](../../_images/math/475fa53c7e34d18f1647d19266e46d14c7e6b8a7.png) .
Durch den Druckwandler wird damit auf das Fluid der rechten Seite,
beispielsweise Hydraulik-Öl, ein wesentlich höhererer Druck
.
Durch den Druckwandler wird damit auf das Fluid der rechten Seite,
beispielsweise Hydraulik-Öl, ein wesentlich höhererer Druck 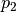 ausgeübt; mit diesem Druck kann wiederum eine hydraulische Anlage betrieben
werden. Dieses Prinzip wird unter anderem in industriellen Einspann-Vorrichtung
verwendet.
ausgeübt; mit diesem Druck kann wiederum eine hydraulische Anlage betrieben
werden. Dieses Prinzip wird unter anderem in industriellen Einspann-Vorrichtung
verwendet.
Statischer Auftrieb in Flüssigkeiten¶
Ist ein Körper mit einem Volumen  von einer Flüssigkeit umgeben, so
erfährt er durch diese eine Auftriebskraft
von einer Flüssigkeit umgeben, so
erfährt er durch diese eine Auftriebskraft 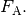 Diese resultiert
aus der Tatsache, dass der Schweredruck innerhalb einer Flüssigkeit mit der
Tiefe zunimmt.
Diese resultiert
aus der Tatsache, dass der Schweredruck innerhalb einer Flüssigkeit mit der
Tiefe zunimmt.
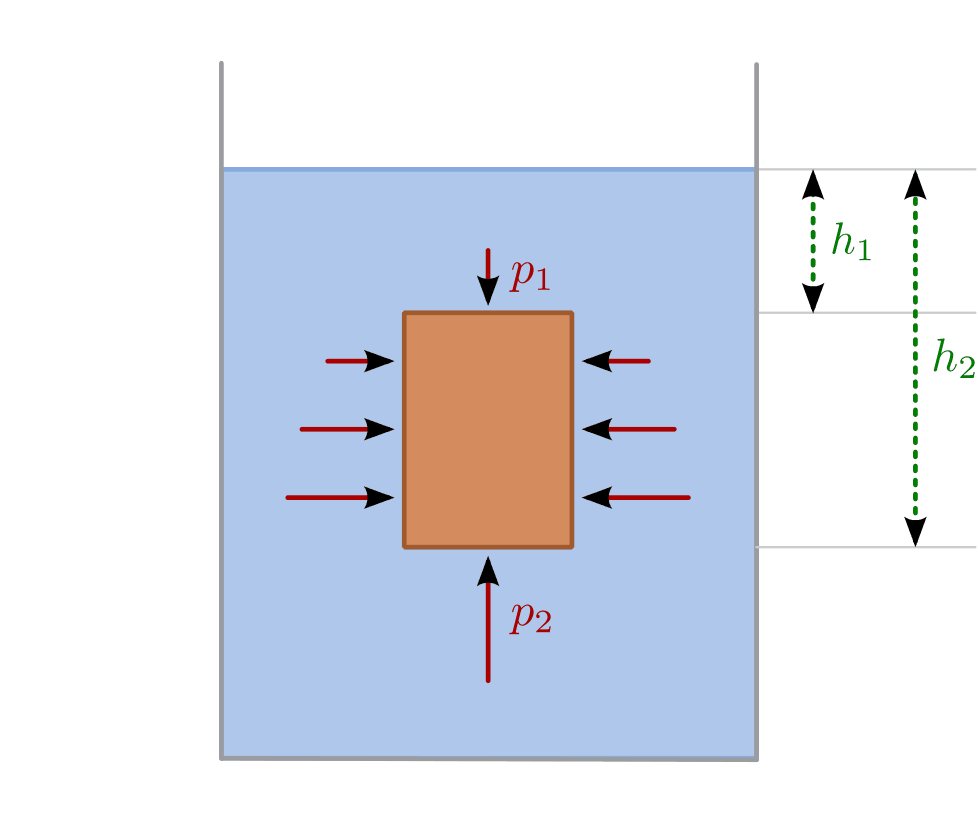
Die horizontalen Kräfte, die durch den Druck der umgebenden Flüssigkeit auf den
Körper einwirken, sind jeweils paarweise gleich groß und heben sich in ihrer
Wirkung gegenseitig auf (sofern der Körper nicht komprimierbar ist). Die nach
unten beziehungsweise oben gerichteten Kräfte 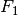 und
und 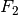 hingegen sind aufgrund der Druckdifferenz unterschiedlich groß.
hingegen sind aufgrund der Druckdifferenz unterschiedlich groß.
Bezeichnet man mit 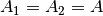 die Grund- beziehungsweise Deckfläche
des Körpers, so gilt:
die Grund- beziehungsweise Deckfläche
des Körpers, so gilt:
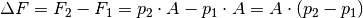
Die Auftriebskraft 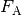 ist mit der Kraftdifferenz
ist mit der Kraftdifferenz
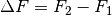 identisch. Zur Berechnung ihres Betrags kann nach
Gleichung (2) für den Schweredruck
identisch. Zur Berechnung ihres Betrags kann nach
Gleichung (2) für den Schweredruck 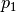 beziehungsweise
beziehungsweise 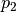 wiederum
wiederum 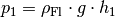 beziehungsweise
beziehungsweise 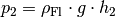 eingesetzt werden, wobei
eingesetzt werden, wobei 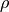 die Dichte der Flüssigkeit bezeichnet:
die Dichte der Flüssigkeit bezeichnet:
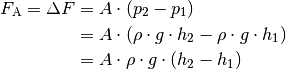
Hierbei bezeichnen 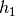 und
und 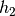 die Eintauchtiefen der Ober-
beziehungsweise Unterseite des Körpers, ihre Differenz
die Eintauchtiefen der Ober-
beziehungsweise Unterseite des Körpers, ihre Differenz 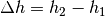 entspricht der Höhe
entspricht der Höhe 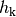 des Körpers. Mit
des Körpers. Mit
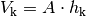 ergibt sich für die
Auftriebskraft folgende Formel:
ergibt sich für die
Auftriebskraft folgende Formel:
(8)¶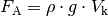
Der Betrag der Auftriebskraft hängt somit ausschließlich von der Dichte
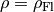 der Flüssigkeit und dem Volumen
der Flüssigkeit und dem Volumen 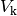 des eintauchenden Körpers ab.
des eintauchenden Körpers ab.
Archimedisches Prinzip und Dichtemessung
Jeder Festkörper verdrängt beim Eintauchen ebenso viel Volumen an Flüssigkeit
wie er selbst an Volumen besitzt; dieser empirisch gefundene Sachverhalt wird
nach seinem Entdecker Archimedes
auch als „Archimedisches Prinzip“ bezeichnet. Da folglich 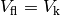 gilt, kann man auf den Index verzichten und einfach
gilt, kann man auf den Index verzichten und einfach  für das Volumen des eintauchenden Körpers beziehungsweise der verdrängten
Flüssigkeit schreiben. Die Auftriebskraft
für das Volumen des eintauchenden Körpers beziehungsweise der verdrängten
Flüssigkeit schreiben. Die Auftriebskraft 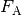 ist also gleich
der Gewichtskraft
ist also gleich
der Gewichtskraft 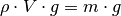 der verdrängten
Flüssigkeit:
der verdrängten
Flüssigkeit:
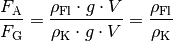
Dieser Zusammenhang kann genutzt werden, um mittels einer Messung der
Gewichtskraft 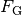 eines Körpers in Luft und der verringerten
Gewichtskraft
eines Körpers in Luft und der verringerten
Gewichtskraft 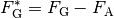 in
Wasser einerseits die Auftriebskraft
in
Wasser einerseits die Auftriebskraft 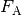 und gleichzeitig, da
die Dichte
und gleichzeitig, da
die Dichte ![\rho_{\mathrm{Wasser}} = \unit[1]{\frac{g}{cm^3}}](../../_images/math/9eda0311ab9f4c0b1bcb880ae8d6b0d822c64c2d.png) bekannt
ist, auch die Dichte
bekannt
ist, auch die Dichte 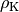 des Körpers zu berechnen:
des Körpers zu berechnen:
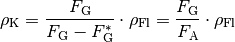
Eine andere Methode zur Bestimmung der Dichte von Festkörpern besteht darin, die Masse des jeweiligen Gegenstands mit Hilfe einer Waage zu ermitteln und mittels eines Messzylinders oder eines Überlaufgefäßes die scheinbare Volumenzunahme der Flüssigkeit beim Eintauchen des Festkörpers zu messen.
Schwimmen, Sinken und Schweben
Die Dichte 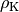 des Körpers hat keine Auswirkung auf die
Auftriebskraft, entscheidet aber darüber, ob er in der Flüssigkeit aufsteigt
(schwimmt), unverändert an gleicher Stelle bleibt (schwebt) oder sich nach unten
bewegt (sinkt).
des Körpers hat keine Auswirkung auf die
Auftriebskraft, entscheidet aber darüber, ob er in der Flüssigkeit aufsteigt
(schwimmt), unverändert an gleicher Stelle bleibt (schwebt) oder sich nach unten
bewegt (sinkt).
Ist
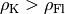 , so ist die Gewichtskraft
, so ist die Gewichtskraft
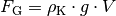 des Körpers größer als
die Auftriebskraft
des Körpers größer als
die Auftriebskraft 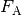 , die der Körper durch das Eintauchen in
die Flüssigkeit erfährt.
, die der Körper durch das Eintauchen in
die Flüssigkeit erfährt.In diesem Fall sinkt der Körper nach unten. Die resultierende Kraft (seine „scheinbare“ Gewichtskraft
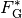 ) ist gleich der Differenz
aus Gewichts- und Auftriebskraft, also:
) ist gleich der Differenz
aus Gewichts- und Auftriebskraft, also: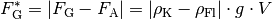
Ist
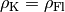 , so ist die Gewichtskraft
, so ist die Gewichtskraft
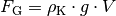 des Körpers gleich der
Auftriebskraft
des Körpers gleich der
Auftriebskraft 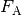 .
.In diesem Fall „schwebt“ der Körper, behält also seine Position bei.
Ist
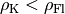 , so ist die Gewichtskraft
, so ist die Gewichtskraft
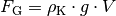 des Körpers kleiner als
die Auftriebskraft
des Körpers kleiner als
die Auftriebskraft 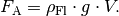
In diesem Fall schwimmt der Körper an der Oberfläche beziehungsweise steigt nach oben. Auch in diesem Fall ist die resultierende Kraft gleich der Differenz aus Gewichts- und Auftriebskraft. Taucht der Körper vollständig ein, so ist sie nach oben (zur Oberfläche der Flüssigkeit hin) gerichtet:
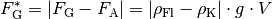
Ein schwimmender Körper befindet sich zum Teil über, zum Teil in der
Flüssigkeit. Er taucht soweit ein, bis sich ein Gleichgewicht zwischen seiner
Gewichtskraft 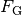 und der Auftriebskraft
und der Auftriebskraft
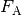 einstellt:
einstellt:
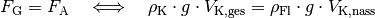
Hierbei kann man den Ortsfaktor 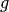 , der auf beiden Seiten der Gleichung
auftritt, kürzen. Löst man die verbleibende Gleichung nach dem eintauchenden
Volumen-Anteil
, der auf beiden Seiten der Gleichung
auftritt, kürzen. Löst man die verbleibende Gleichung nach dem eintauchenden
Volumen-Anteil 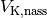 des Körpers auf, so folgt:
des Körpers auf, so folgt:
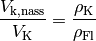
Der eintauchende Anteil des Körpervolumens 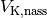 entspricht also dem Verhältnis
entspricht also dem Verhältnis
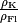 der Dichten des
schwimmenden Körpers und der Flüssigkeit.[3]
der Dichten des
schwimmenden Körpers und der Flüssigkeit.[3]
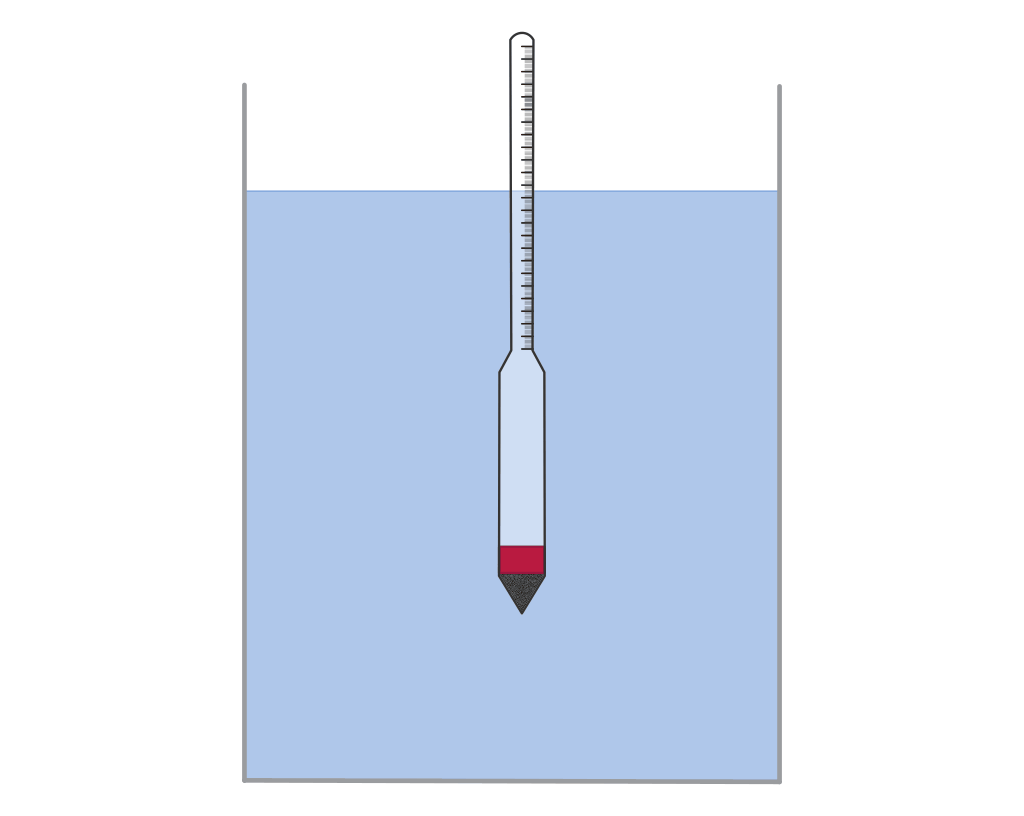
Dieses Prinzip wird beispielsweise bei so genannten Senkwaagen („Aräometer“)
genutzt. Diese bestehen aus einem hohlen Glaskörper mit einem Volumen
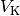 , der am unteren Ende mit Bleischrot gefüllt ist und am
oberen Ende eine Skala zum unmittelbaren Ablesen der Flüssigkeitsdichte
enthält. Je geringer die Dichte der Flüssigkeit ist, desto tiefer taucht das
Aräometer in die Flüssigkeit ein.
, der am unteren Ende mit Bleischrot gefüllt ist und am
oberen Ende eine Skala zum unmittelbaren Ablesen der Flüssigkeitsdichte
enthält. Je geringer die Dichte der Flüssigkeit ist, desto tiefer taucht das
Aräometer in die Flüssigkeit ein.
Die genannte Form des Auftriebs wird „statischer“ Auftrieb genannt. Es gilt sowohl, wenn sich der eintauchende Körper und die Flüssigkeit relativ zueinander bewegen als auch wenn sich Körper und Flüssigkeit in der Ruhelage befinden.
Kontinuitäts- und Bernoulli-Gleichung¶
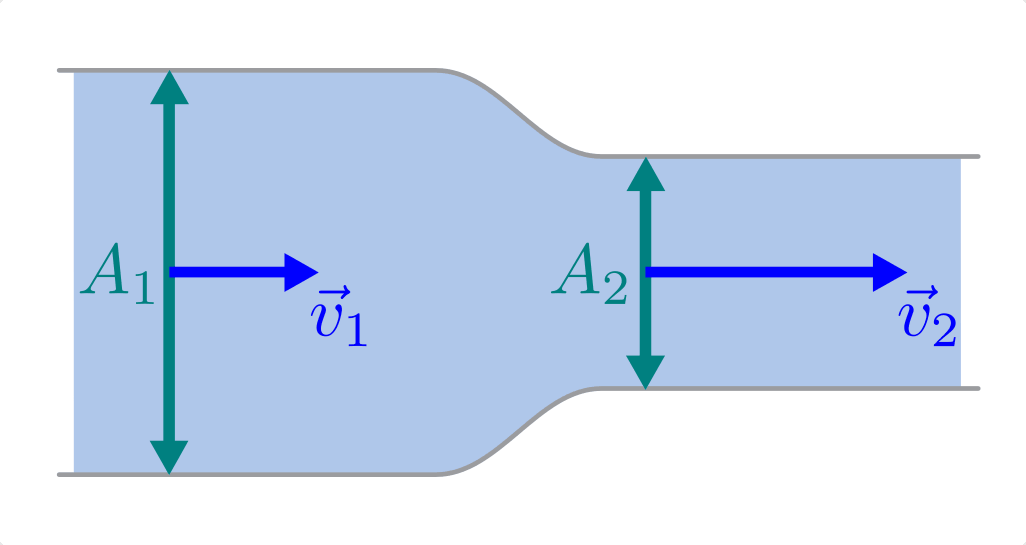
Fließt eine Flüssigkeit kontinuierlich durch ein Rohrleitungssystem ohne Speichermöglichkeiten, so strömt in jedes beliebige Volumenelement immer genauso viel Masse hinein wie auch wieder heraus strömt („Kontinuitätsbedingung“). Kann die Reibung vernachlässigt werden und ist die Flüssigkeit inkompressibel, so muss damit an engen Stellen des Rohrsystems eine höhere Strömungsgeschwindigkeit auftreten als an Bereichen mit weitem Rohrquerschnitt.
Die Kontinuistätsgleichung
Dieser Effekt lässt sich durch eine Formel auch quantitativ bestimmen. Ist die
Flüssigkeit inkompressibel, so ist ihre Dichte 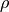 an allen Stellen
gleich. Wegen
an allen Stellen
gleich. Wegen 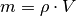 gilt für den fließenden Masse-Strom
gilt für den fließenden Masse-Strom
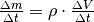 ; soll
der Masse-Strom konstant bleiben, so muss aufgrund der konstanten Dichte
folglich auch der Volumen-Strom
; soll
der Masse-Strom konstant bleiben, so muss aufgrund der konstanten Dichte
folglich auch der Volumen-Strom 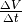 an allen
Stellen gleich sein:
an allen
Stellen gleich sein:
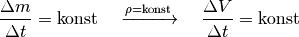
Das Volumen  der Flüssigkeit wiederum lässt sich als Produkt der
Querschnittsfläche
der Flüssigkeit wiederum lässt sich als Produkt der
Querschnittsfläche  des betrachteten Rohrstücks und der durchlaufenen
Strecke
des betrachteten Rohrstücks und der durchlaufenen
Strecke  beschreiben. Somit gilt:
beschreiben. Somit gilt:
Durch zwei benachbarte Rohrstücke mit den Querschnitten 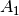 und
und
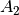 fließt aufgrund der Kontinuitätsbedingung stets ein gleicher Massen-
beziehungsweise Volumenstrom. Für die Strömungsgeschwindigkeiten
fließt aufgrund der Kontinuitätsbedingung stets ein gleicher Massen-
beziehungsweise Volumenstrom. Für die Strömungsgeschwindigkeiten 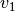 und
und
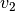 in den Rohrstücken gilt also:
in den Rohrstücken gilt also:
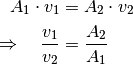
Bei einer reibungslosen Flüssigkeit verhalten sich die Strömungsgeschwindigkeiten somit umgekehrt proportional zum Rohrquerschnitt.
Die Bernoulli-Gleichung
Überprüft man mit einem Manometer an verschiedenen Stellen der Rohrleitung den
statischen Druck 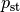 der Flüssigkeit, so zeigt sich, dass an
den engen Stellen mit größeren Geschwindigkeiten geringere statische
Druckwerte gemessen werden. Diese zunächst etwas verblüffend wirkende Tatsache
wird als „hydrodynamisches Paradoxon“ bezeichnet.
der Flüssigkeit, so zeigt sich, dass an
den engen Stellen mit größeren Geschwindigkeiten geringere statische
Druckwerte gemessen werden. Diese zunächst etwas verblüffend wirkende Tatsache
wird als „hydrodynamisches Paradoxon“ bezeichnet.
Man kann dieses Phänomen dadurch erklärt, dass an allen Stellen der Flüssigkeit
ein gleich großer Gesamtdruck 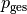 vorliegt. Dieser
Gesamtdruck wiederum ist gleich der Summe des statischen Drucks
vorliegt. Dieser
Gesamtdruck wiederum ist gleich der Summe des statischen Drucks
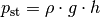 und des dynamischen Drucks
(„Staudruck“)
und des dynamischen Drucks
(„Staudruck“) 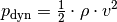 der
Flüssigkeit:[4]
der
Flüssigkeit:[4]
(9)¶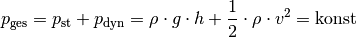
Dieser Zusammenhang wird als Bernoulli-Gleichung bezeichnet: Nimmt in einem geschlossenen Rohrsystem der dynamische Druck aufgrund einer zunehmenden Strömungsgeschwindigkeit zu, so muss gleichzeitig der statische Druck abnehmen.
Während der statische Druck 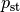 gleichmäßig in alle
Richtungen wirkt, wirkt der dynamische Druck
gleichmäßig in alle
Richtungen wirkt, wirkt der dynamische Druck 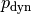 ausschließlich auf Flächen, die senkrecht zur Strömungsrichtung stehen.
ausschließlich auf Flächen, die senkrecht zur Strömungsrichtung stehen.
Formal hat die Bernoulli-Gleichung eine große Verwandschaft mit dem Energie-Erhaltungssatz der Mechanik: Dieser besagt, dass in einem isolierten System ohne Reibungseffekte die Summe aus potentieller und kinetischer Energie erhalten bleibt:
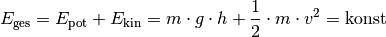
Tatsächlich erhält man die Bernoulli-Gleichung, wenn man in der obigen Gleichung
zunächst 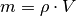 schreibt und anschließend die Gleichung durch
schreibt und anschließend die Gleichung durch
 dividiert. Der Gesamtdruck in einem geschlossenen Rohrsystem
entspricht somit einer Energiedichte.
dividiert. Der Gesamtdruck in einem geschlossenen Rohrsystem
entspricht somit einer Energiedichte.
Die Bernoulli-Gleichung wird in zahlreichen technischen Bereichen genutzt:
- Bei einer Wasserstrahlpumpe lässt man Wasser durch eine sich verengendes
Rohrstück strömen. Mit der zunehmenden Wassergeschwindigkeit an der offenen
Engstelle nimmt der ausschließlich in Strömungsrichtung wirkende dynamische
Druck
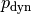 zu, der allseitig wirkende statische Druck
zu, der allseitig wirkende statische Druck
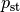 hingegen ab. Als Folge davon wird Luft (oder ein
anderes Fluid) durch den Seitenstutzen „angesaugt“.
hingegen ab. Als Folge davon wird Luft (oder ein
anderes Fluid) durch den Seitenstutzen „angesaugt“.
- Zerstäuber in Sprayflaschen funktionieren auf ähnliche Weise: Vor der Düse sorgt eine schnelle Luftströmung für eine Reduzierung des statischen Luftdrucks und damit für ein „Ansaugen“ der Flüssigkeit in dem Zerstäuberrohr.
- Mit einer so genannten Messblende kann die Strömungsgeschwindigkeit eines Fluids in einer Röhre bestimmt werden.
Das obige Bernoulli-Prinzip gilt nicht nur für Flüssigkeiten, sondern auch für Gase, wobei es für die Flugfähigkeit von Körpern von entscheidender Bedeutung ist („dynamischer Auftrieb“). In beiden Fällen müssen allerdings bei kleinen Rohrdurchmessern und/oder hohen Strömungsgeschwindigkeiten Reibungseffekte und Turbulenzen berücksichtigt werden.
Viskosität (innere Reibung)¶
Ist die Reibung innerhalb einer Flüssigkeit nicht vernachlässigbar, so ist eine Kraft beziehungsweise ein Druck nötig, um eine Flüssigkeit gegenüber einem Rohrsystem gleichmäßig zu bewegen. Wie groß die nötige Schubkraft ist, hängt von der Viskosität („Zähigkeit“) der Flüssigkeit ab.
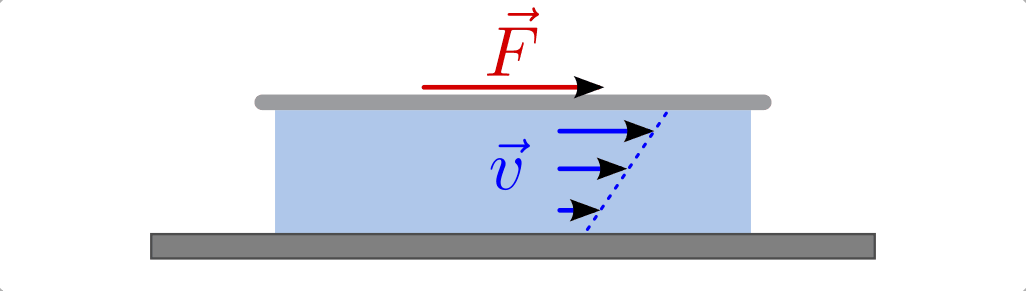
Geschwindigkeitsprofil zweier aneinander gleitender Platten mit einer dünnen, viskosen Flüssigkeitsschicht.
Legt man beispielsweise ein Deckglas auf einen Flüssigkeitstropfen und
verschiebt es auf der dünnen Flüssigkeitsschicht langsam und gleichmäßig
entlang der Grundfläche, so ist zum Aufrechthalten der Bewegung eine Kraft
 erforderlich. Diese Kraft ist proportional zur Fläche
erforderlich. Diese Kraft ist proportional zur Fläche  des
Glases, zur Geschwindigkeit
des
Glases, zur Geschwindigkeit  der Bewegung und zur Viskosität
der Bewegung und zur Viskosität
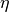 der Flüssigkeit; zudem ist die Kraft umgekehrt proportional zur
Dicke
der Flüssigkeit; zudem ist die Kraft umgekehrt proportional zur
Dicke  der Flüssigkeitsschicht. Insgesamt gilt also für diese zur
Überwindung der Reibung nötige Kraft
der Flüssigkeitsschicht. Insgesamt gilt also für diese zur
Überwindung der Reibung nötige Kraft 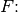
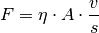
Die obige Gleichung kann auch umgeformt werden, um ein Maß für die Viskosität einer Flüssigkeit zu erhalten:
(10)¶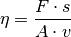
Die Einheit der Viskosität kann nach der obigen Formel als „Pascalsekunde“ ausgedrückt werden:
![[\eta] = \unit{\frac{N \cdot m}{m^2 \cdot \frac{m}{s}}} = \unit{\frac{N
\cdot s}{m^2}} = \unit{Pa \cdot s}](../../_images/math/0e63e247c807b545fabf1aa3d9e334a05078b5c1.png)
Viskositäten von Flüssigkeiten werden üblicherweise bei einer Temperatur von
![\unit[20]{\degree C}](../../_images/math/5306d44af8f7df91464b32ed64cda4ded46190b0.png) angegeben, da sie stark temperaturabhängig sind.
Bei den meisten Flüssigkeiten nimmt die Viskosität mit zunehmender Temperatur
stark ab, bei Gasen ist es umgekehrt.[5]
angegeben, da sie stark temperaturabhängig sind.
Bei den meisten Flüssigkeiten nimmt die Viskosität mit zunehmender Temperatur
stark ab, bei Gasen ist es umgekehrt.[5]
Wasser hat bei ![\unit[20]{\degree C}](../../_images/math/5306d44af8f7df91464b32ed64cda4ded46190b0.png) eine Viskosität von nahezu exakt
eine Viskosität von nahezu exakt
![\unit[\frac{1}{1000}]{Pa \cdot s} = \unit[1]{mPa \cdot s}](../../_images/math/acf9d8396548b6ba0e8ef307631ded14f3cedc8b.png) . Da viele
weitere Flüssigkeiten ähnliche Viskositätswerte aufweisen, wird die Viskosität
in Tabellen allgemein oft in Millipaskalsekunden angeben.[6]
. Da viele
weitere Flüssigkeiten ähnliche Viskositätswerte aufweisen, wird die Viskosität
in Tabellen allgemein oft in Millipaskalsekunden angeben.[6]
| Substanz | Viskosität 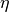 in in 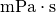 |
| Aceton | 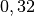 |
| Benzol | 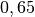 |
| Blut | 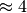 |
| Ethanol | 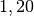 |
| Glycerin | 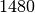 |
| Olivenöl | 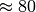 |
| Sirup | 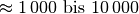 |
Wasser (![\unit[10]{\degree C}](../../_images/math/4a31ca78b8545be3309cc8a125648306158e1d61.png) ) ) |
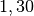 |
Wasser (![\unit[20]{\degree C}](../../_images/math/5306d44af8f7df91464b32ed64cda4ded46190b0.png) ) ) |
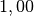 |
Wasser (![\unit[30]{\degree C}](../../_images/math/1bb5f6a9033ac83bafca20f9012dcdb9d6b9c294.png) ) ) |
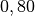 |
Messung der Viskosität einer Flüssigkeit
Experimentell kann die Viskosität einer Flüssigkeit mit folgenden Methoden bestimmt werden:
Bei Kugelfall-Viskosimetern lässt man eine Kugel mit einem Radius
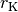 und einer Dichte
und einer Dichte 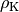 in einem
Behälter absinken, der mit der zu untersuchenden Flüssigkeit gefüllt ist.
in einem
Behälter absinken, der mit der zu untersuchenden Flüssigkeit gefüllt ist.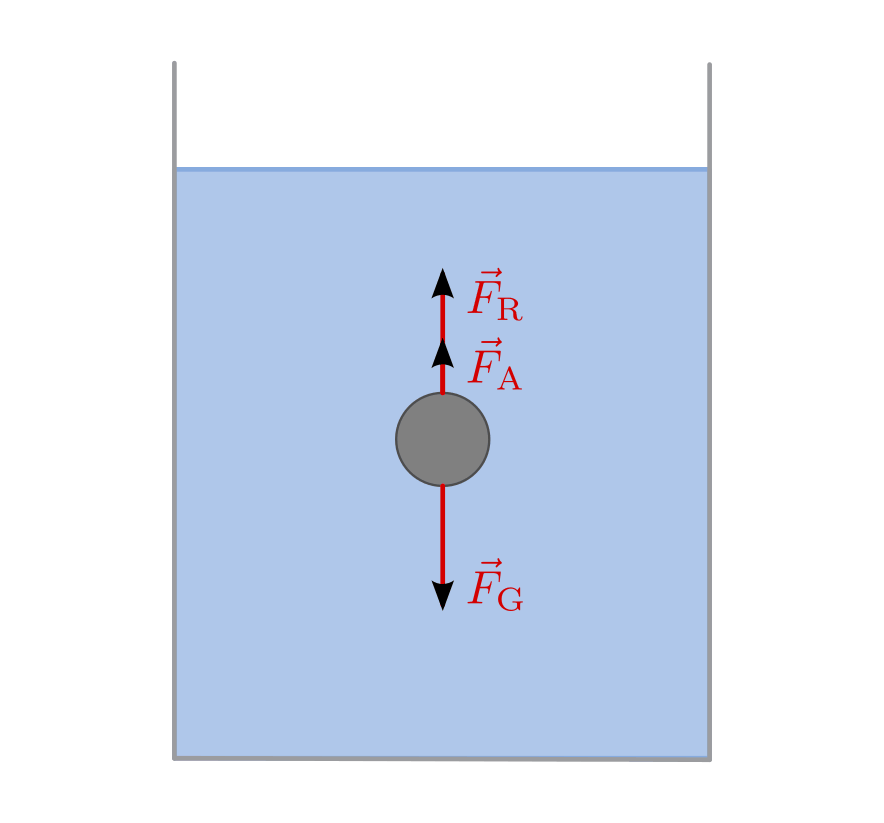
Prinzip eines Kugelfall-Viskosimeters: Die Kugel sinkt aufgrund des Kräfte-Gleichgewichts mit konstanter Geschwindigkeit
Die Kugel erfährt in diesem Fall eine von ihrer Geschwindigkeit
 abhängige Reibungskraft, für die George Stokes folgende Formel fand:
abhängige Reibungskraft, für die George Stokes folgende Formel fand: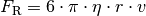
Mit einer zunehmenden Sink-Geschwindigkeit der Kugel wird auch die wirkende Reibungskraft größer, bis sich ein Kräfte-Gleichgewicht zwischen der Stokeschen Reibungskraft, der Gewichtskraft
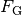 der Kugel
und der Auftriebskraft
der Kugel
und der Auftriebskraft 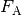 einstellt:
einstellt:![F_{\mathrm{R}} &= F_{\mathrm{G}} - F_{\mathrm{A}} \\[6pt]
6 \cdot \pi \cdot \eta \cdot r_{\mathrm{K}}\cdot v &= (\rho_{\mathrm{K}} -
\rho_{\mathrm{Fl}}) \cdot V_{\mathrm{K}} \cdot g \\[6pt]
\eta &= \frac{(\rho_{\mathrm{K}} - \rho_{\mathrm{Fl}}) \cdot
V_{\mathrm{K}} \cdot g}{6 \cdot \pi \cdot r_{\mathrm{K}} \cdot v}
\\[6pt]](../../_images/math/4764fff1fa8221ec2808b4a45614562ddd98ebb3.png)
Die Viskosität der Flüssigkeit kann also unmittelbar berechnet werden, wenn die Dichten der Flüssigkeit und der Kugel sowie der Kugelradius bekannt sind und die Geschwindigkeit der konstant sinkenden Kugel gemessen wird.
Bei Rotationsviskosimetern wird ein Zylinder in ein ebenfalls zylindrisches Messgefäß mit einem etwas größeren Durchmesser getaucht. Zwischen beide Zylinderoberflächen wird die zu prüfende Flüssigkeit gefüllt; dann wird mit einem Motor üblicherweise der innere Zylinder gleichmäßig gegen den äußeren gedreht und das dafür nötige Drehmoment als Maß für die wirkende Reibungskraft und somit – da die Zylindermasse bekannt sind – für die Viskosität gemessen. Bei professionellen Laborgeräten erfolgt die Auswertung automatisch über einen Mikroprozessor, der den berechneten Viskositätswert zugleich über ein Display ausgibt.
Bei Kapillarviskosimetern lässt man ein bestimmtes Volumen der zu prüfenden Flüssigkeit durch ein dünnes, senkrecht aufgehängtes Glasrohr fließen. Die Viskosität der Flüssigkeit kann durch Messung der Durchlaufzeit
 berechnet werden, indem man diese mit der Dichte
berechnet werden, indem man diese mit der Dichte 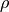 der Flüssigkeit
und einer für den Apparat angegebenen Konstanten
der Flüssigkeit
und einer für den Apparat angegebenen Konstanten 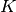 multipliziert.
multipliziert.
Laminare und turbulente Strömungen¶
Bei geringen Geschwindigkeiten treten häufig so genannte laminare Strömungen auf. Dabei bewegen sich die Flüssigkeitsteilchen, als würden sie sich in übereinander geschichteten Lamellen befinden. Das Geschwindigkeitsprofil in einem zylindrischen Rohr ist dabei parabelförmig und nimmt zur Mitte des Rohres hin zu.
Das Hagen-Poiseuillesche Gesetz
Für laminare Strömungen eines Fluids durch ein Rohr mit einem Radius  und einer Länge
und einer Länge  haben Gotthilf Hagen und Jean
Poiseuille
folgende Formel entdeckt, die auch die Viskosität
haben Gotthilf Hagen und Jean
Poiseuille
folgende Formel entdeckt, die auch die Viskosität 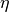 der Flüssigkeit
berücksichtigt:
der Flüssigkeit
berücksichtigt:
(11)¶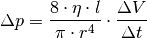
Berücksichtigt man die Viskosität 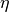 und somit Reibungseffekte
zwischen der Flüssigkeit und den Gefäßwänden, so bleibt der Gesamtdruck in einem
geschlossenen Rohrsystem nicht konstant, sondern sinkt mit zunehmender zur Länge
und somit Reibungseffekte
zwischen der Flüssigkeit und den Gefäßwänden, so bleibt der Gesamtdruck in einem
geschlossenen Rohrsystem nicht konstant, sondern sinkt mit zunehmender zur Länge
 des Rohrsystems ab. Die obige Formel beschreibt den zusätzlichen Druck
des Rohrsystems ab. Die obige Formel beschreibt den zusätzlichen Druck
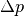 zwischen dem Anfang und dem Ende des Rohrsystems, der zum
Aufrechterhalten des Volumenstroms
zwischen dem Anfang und dem Ende des Rohrsystems, der zum
Aufrechterhalten des Volumenstroms 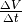 notwendig
ist.
notwendig
ist.
Das Hagen-Poiseuillesche Gesetz wurde unter Annahme der folgenden Bedingungen formuliert:
- Der Rohrdurchmesser
 ist konstant.
ist konstant. - Es wirken keine äußeren Kräfte durch die Rohrwand hindurch.
- Es treten ausschließlich Reibungskräfte, jedoch keine Trägheitskräfte auf. Dies ist der Fall, wenn die Flüssigkeit während der Bewegung im Rohr nicht beschleunigt wird. Man spricht in diesem Fall von einer „stationären“, also einer sich zeitlich nicht ändernden, Strömung.
- Die Flüssigkeitsteilchen an der Rohrwand sind in Ruhe, für sie gilt also
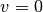 . Haftet die Flüssigkeit nicht an der Rohrwand, so wird dies
vom Hagen-Poiseuilleschen Gesetz nicht berücksichtigt.
. Haftet die Flüssigkeit nicht an der Rohrwand, so wird dies
vom Hagen-Poiseuilleschen Gesetz nicht berücksichtigt. - Die Dichte
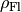 der Flüssigkeit ist konstant, sie ändert
sich also mit zunehmendem Druck nicht. Eine solche Inkompressibilität gilt in
sehr guter Näherung für Flüssigkeiten, bei Gasen nur bei nicht zu hohen
Strömungsgeschwindigkeiten.
der Flüssigkeit ist konstant, sie ändert
sich also mit zunehmendem Druck nicht. Eine solche Inkompressibilität gilt in
sehr guter Näherung für Flüssigkeiten, bei Gasen nur bei nicht zu hohen
Strömungsgeschwindigkeiten.
In der Praxis wird das Hagen-Poiseuillesche üblicherweise für die Beschreibung von zähflüssigen Fluiden in engen Rohrsystemen genutzt, in denen die obigen Bedingungen zumindest näherungsweise erfüllt sind. Von besonderer Bedeutung ist, dass der zum Aufrechterhalten des Volumenstroms benötigte Druck mit indirekt proportional zur vierten Potenz des Gefäß-Radius zunimmt; dies bedeutet beispielsweise für den menschlichen Körper, dass eine zunehmende Verengung der Blutgefäße – insbesondere durch zu viel Cholesterin bei der Nahrungsaufnahme – mit Bluthochdruck und der Gefahr von Herzkrankheiten einher geht.
Newtonsche Flüssigkeiten
Sind die Bedingungen für das Hagen-Poiseuillesche Gesetz erfüllt, so ist für
eine Vergrößerung des Volumenstroms 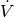 eine proportional größere
Druckdifferenz
eine proportional größere
Druckdifferenz 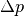 nötig. Trägt man die Volumenstromstärke als
Funktion der Druckdifferenz aus, so ergibt sich eine Gerade. Fluide, auf die
dieses Verhalten zutrifft, bezeichnet man als „Newtonsche Flüssigkeiten“.
nötig. Trägt man die Volumenstromstärke als
Funktion der Druckdifferenz aus, so ergibt sich eine Gerade. Fluide, auf die
dieses Verhalten zutrifft, bezeichnet man als „Newtonsche Flüssigkeiten“.
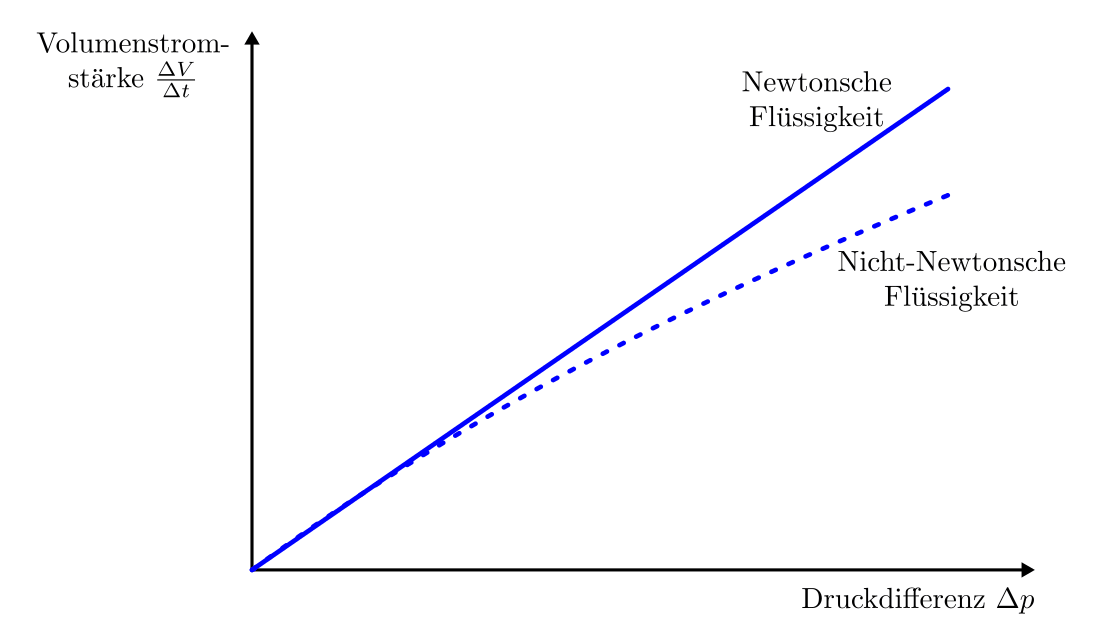
Volumenstromstärke-Druckdifferenz-Diagramm einer Newtonschen und einer Nicht-Newtonschen Flüssigkeit.
Da im Hagen-Poiseuillen Gesetz alle Größen bis auf 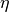 direkt messbar
sind, kann es auch zur experimentellen Bestimmung der Zähigkeit eines Fluids
genutzt werden.
direkt messbar
sind, kann es auch zur experimentellen Bestimmung der Zähigkeit eines Fluids
genutzt werden.
Strömungswiderstand
Setzt man die Druckdifferenz 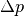 zwischen Anfang und Ende einer
Rohrleitung in Relation zum Volumenstrom
zwischen Anfang und Ende einer
Rohrleitung in Relation zum Volumenstrom 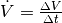 , so erhält man den so genannten Strömungswiderstand
, so erhält man den so genannten Strömungswiderstand 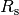 .
Es gilt also:
.
Es gilt also:
(12)¶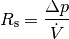
Der Strömungswiderstand ist nicht nur abhängig von der Geometrie des Rohres,
sondern auch noch von der Zähigkeit der durchströmenden Flüssigkeit; er wird in
der Einheit 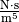 angegeben. Der Kehrwert des
Strömungswiderstands wird „Leitwert“ einer Kapillare genannt:
angegeben. Der Kehrwert des
Strömungswiderstands wird „Leitwert“ einer Kapillare genannt:
(13)¶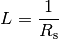
Setzt man das Hagen-Poiseuillesche Gesetz (11) in die
Definition des Strömungswiderstand ein, so ergibt sich mit 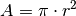 beziehungsweise
beziehungsweise 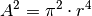 folgende Formel für den
Strömungswiderstand in einem Rohr mit runder Querschnittsfläche:
folgende Formel für den
Strömungswiderstand in einem Rohr mit runder Querschnittsfläche:
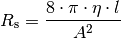
Je geringer der Strömungswiderstand einer Newtonschen Flüssigkeit in einem Gefäß
ist, desto steiler verläuft die Gerade im obigen
Volumenstromstärke-Druckdifferenz-Diagramm. Da der Strömungswiderstand sowohl
proportional zur Druckdifferenz 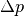 als auch proportional zur Länge
als auch proportional zur Länge
 des Rohres ist, ergibt sich auch ein direkt proportionaler
Zusammenhang zwischen
des Rohres ist, ergibt sich auch ein direkt proportionaler
Zusammenhang zwischen 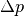 und
und 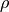 : Bei konstantem
Durchmesser nimmt der Druck linear mit der Länge
: Bei konstantem
Durchmesser nimmt der Druck linear mit der Länge  des Rohres ab.
des Rohres ab.
Muss eine Flüssigkeit mehrere Gefäße mit den Strömungswiderständen
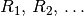 nacheinander durchlaufen, so ist der insgesamt
auftretende Strömungswiderstand
nacheinander durchlaufen, so ist der insgesamt
auftretende Strömungswiderstand 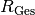 gleich der Summe aller
Teilwiderstände.
gleich der Summe aller
Teilwiderstände.
Für eine „Reihenschaltung“ mehrerer Strömungswiderstände gilt also:
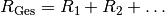
Können im umgekehrten Fall mehrere Kapillaren parallel durchlaufen werden, so
addieren sich die Kehrwerte der Strömungswiderstände zum Kehrwert des
Gesamtwiderstands. Da der Kehrwert des 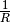 eines
Strömungswiderstands mit dem Leitwert
eines
Strömungswiderstands mit dem Leitwert 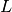 identisch ist, können in diesem
Fall also auch die Leitwerte addiert werden.
identisch ist, können in diesem
Fall also auch die Leitwerte addiert werden.
Für eine „Parallelschaltung“ mehrerer Strömungswiderstände gilt somit:
![{\color{white}bzw. \quad }\frac{1}{R_{\mathrm{Ges}}} &= \frac{1}{R_1} + \frac{1}{R_2} + \ldots \quad
\text{bzw.} \\[8pt] L_{\mathrm{Ges}} &= L_1 + L_2 + \ldots](../../_images/math/7ae627cdcc3c62e472d8726cae9178fd7dfe3004.png)
Bei einer Reihenschaltung ist der Gesamt-Strömungswiderstand somit größer als der größte Teilwiderstand, bei einer Parallelschaltung geringer als der kleinste Teilwiderstand.
Die Reynolds-Zahl
Bei höheren Geschwindigkeiten und ungleichen Wandformen (z.B. Ecken, vorstehende
Teile) können Wirbel entstehen, die von der Strömung mit transportiert werden;
der Strömungswiderstand steigt dabei erheblich an. Eine mathematische Berechnung
von derartigen „turbulenten“ Strömungen ist sehr aufwendig; mit Hilfe der von
Osborne Reynolds
beschriebenen und nach ihm benannten „Reynolds-Zahl“ kann jedoch grob
abgeschätzt werden, ob bei einer Strömung laminares oder turbulentes Verhalten
zu erwarten ist. Die Reynolds-Zahl 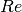 berechnet sich wie folgt:
berechnet sich wie folgt:
(14)¶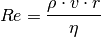
Dabei bezeichnet 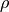 die Dichte des Fluids,
die Dichte des Fluids,  seine
Strömungsgeschwindigkeit,
seine
Strömungsgeschwindigkeit, 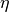 seine Viskosität und
seine Viskosität und  den Radius
des Rohres, durch den das Fluid strömt. Die Reynolds-Zahl selbst ist ein reiner
Zahlenwert ohne Einheit. Ist ihr Wert für eine Strömung kleiner als
den Radius
des Rohres, durch den das Fluid strömt. Die Reynolds-Zahl selbst ist ein reiner
Zahlenwert ohne Einheit. Ist ihr Wert für eine Strömung kleiner als
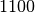 , so kann von einer laminaren Strömung ausgegangen werden, bei
größeren Werten ist mit Wirbelbildungen zu rechnen.
, so kann von einer laminaren Strömung ausgegangen werden, bei
größeren Werten ist mit Wirbelbildungen zu rechnen.
Im menschlichen Blutkreislauf tritt turbulente Strömung normalerweise nur in
der herznahen Aorta bei einer Strömungsgeschwindigkeit von ![\unit[50
\text{ bis } 70]{\frac{cm}{s}}](../../_images/math/b0a0a166124a21446f9ee4fa440bc82ff9561007.png) auf. Rauhe Stellen, beispielsweise bei
Venenentzündungen, können allerdings ebenfalls Wirbelbildungen begünstigen
und zur Entstehung von Thrombosen führen.
auf. Rauhe Stellen, beispielsweise bei
Venenentzündungen, können allerdings ebenfalls Wirbelbildungen begünstigen
und zur Entstehung von Thrombosen führen.
Oberflächenspannung und Kapillarität¶
Kräfte, die zwischen den Molekülen einer einzelnen Substanz wirken, bezeichnet man als Kohäsionskräfte.[7] Im Inneren einer Flüssigkeit heben sich durch das Zusammenwirken mehrerer Kräfte die einzelnen auf jedes Molekül wirkenden Kohäsionskräfte gegenseitig (weitgehend) auf. An der Oberfläche jedoch erfahren die Moleküle eine nach innen gerichtete resultierende Kraft, welche beispielsweise die Moleküle einer Flüssigkeit in einem Tropfen zusammenhält.
Durch die an der Oberfläche nach innen gerichteten Kohäsionskräfte ist die Oberfläche einer freien Flüssigkeit stets minimal. Einzelne Flüssigkeitstropfen besitzen eine Kugelform, da bei einem bestimmten Volumen die Kugel derjenige geometrische Körper mit der geringsten Oberfläche ist.
Möchte man ein Molekül von der Oberfläche einer Flüssigkeit „anheben“ oder
herauslösen, so muss Arbeit gegen die Kohäsionskräfte verrichtet werden. Das
Verhältnis aus der nötigen Arbeit 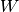 und der dadurch resultierenden
Vergrößerung
und der dadurch resultierenden
Vergrößerung 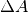 der Oberfläche wird spezifische Oberflächenenergie
oder kurz Oberflächenspannung
der Oberfläche wird spezifische Oberflächenenergie
oder kurz Oberflächenspannung  genannt:
genannt:
(15)¶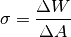
Die Einheit der Oberflächenspannung ist 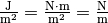 ; die Oberflächenspannung ist
also eigentlich eine Energiemenge je Fläche.
; die Oberflächenspannung ist
also eigentlich eine Energiemenge je Fläche.
| Substanz | Oberflächenspannung 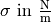 |
| Aceton | 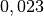 |
| Ethanol | 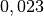 |
| Glycerin | 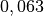 |
| Quecksilber | 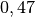 |
| Seifenlösung | 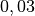 |
| Wasser | 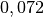 |
Die Oberflächenspannung eines Materials ist allgemein temperaturabhängig; am Gefrierpunkt ist sie am größten, mit zunehmender (absoluter) Temperatur wird sie geringer. Gelöste Stoffe oder Verunreinigungen können ebenfalls eine starke Verringerung der Oberflächenspannung bewirken, beispielsweise hat eine Seifenlösung eine deutlich geringere Oberflächenspannung als reines Wasser.
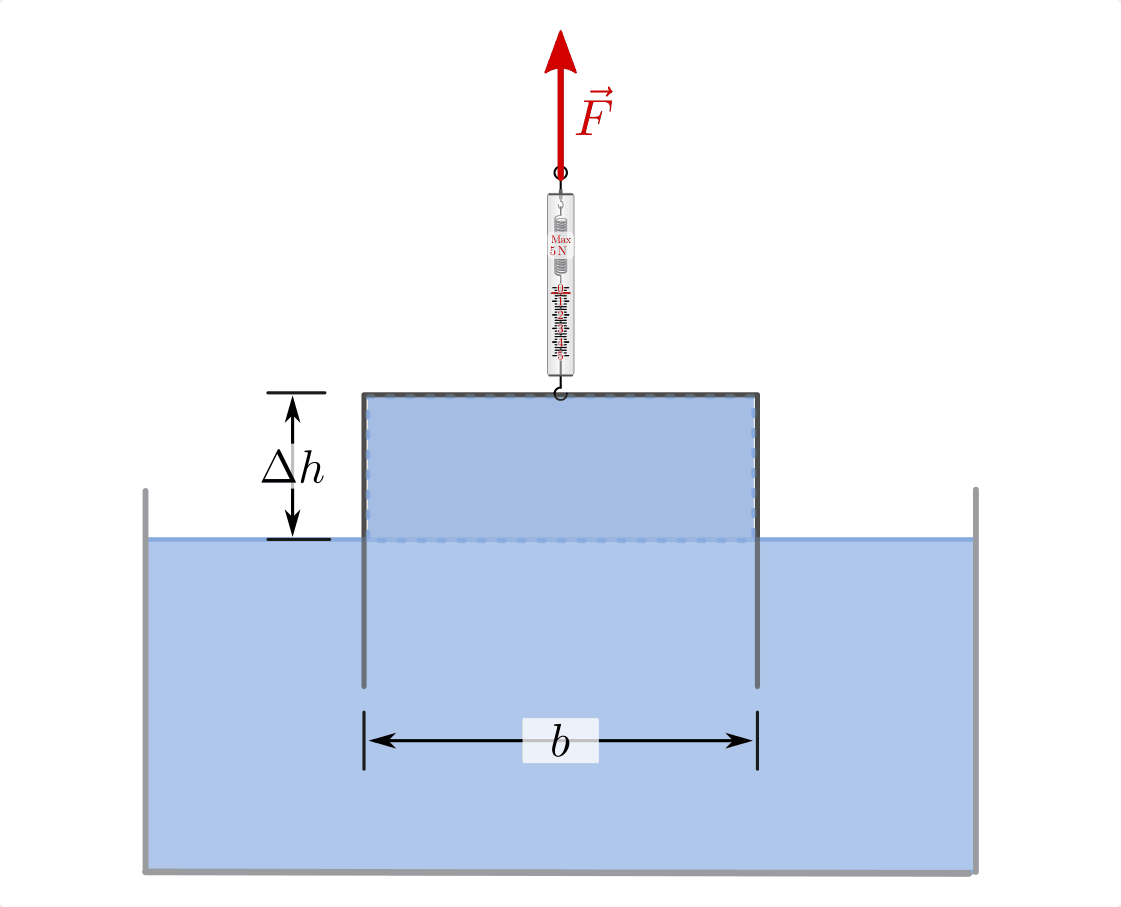
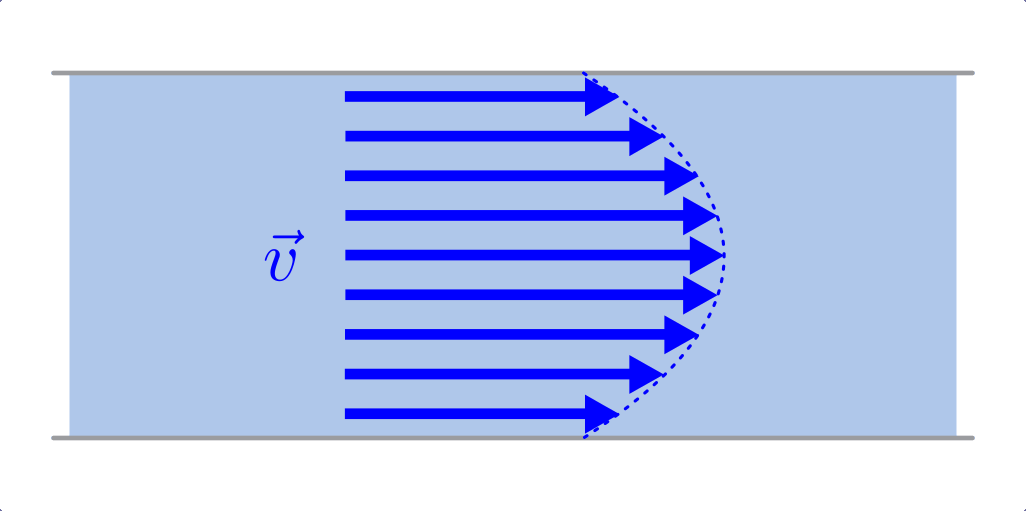
Experimentelle Bestimmung der Oberflächenspannung durch Herausziehen einer „Wasserhaut“ mittels eines Drahtbügels.
Um die Oberflächenspannung einer Flüssigkeit experimentell zu bestimmen, kann
man beispielsweise – ähnlich wie beim Seifenblasen-Machen – mittels eines
Drahtbügels eine dünne Schicht aus der Flüssigkeitsoberfläche „herausziehen“.
Hat der Drahtbügel die Breite 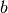 und wird dieser um eine Höhe
und wird dieser um eine Höhe
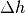 angehoben, so gilt für die verrichtete mechanische Arbeit:
angehoben, so gilt für die verrichtete mechanische Arbeit:
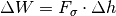
Mit 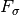 wird dabei die zum Herausziehen des Drahtes
notwendige Kraft bezeichnet. Für die Vergrößerung der Flüssigkeits-Oberfläche
wird dabei die zum Herausziehen des Drahtes
notwendige Kraft bezeichnet. Für die Vergrößerung der Flüssigkeits-Oberfläche
 gilt:
gilt:
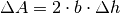
Der Faktor 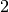 ergibt sich daraus, dass sowohl auf der Vorder- wie auch
auf der Hinterseite des Bügels eine zusätzliche Oberfläche mit einer Größe von
ergibt sich daraus, dass sowohl auf der Vorder- wie auch
auf der Hinterseite des Bügels eine zusätzliche Oberfläche mit einer Größe von
 hinzukommt. Für die Oberflächenspannung
hinzukommt. Für die Oberflächenspannung  ergibt sich damit:
ergibt sich damit:
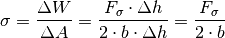
Anders als bei einer Schraubenfeder ist die zum Herausziehen des Drahtes
benötigte Zugkraft 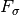 , wie man an der oberen Formel
erkennen kann, unabhängig von dem Betrag der „Dehnung“
, wie man an der oberen Formel
erkennen kann, unabhängig von dem Betrag der „Dehnung“ 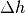 :
:
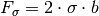
Ein wichtiger Sonderfall dieser Gleichung ergibt sich, wenn der Draht
zu einem Ring gebogen wird. Die Bogenlänge 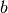 entspricht dann einem
ganzen Kreisumfang, also
entspricht dann einem
ganzen Kreisumfang, also 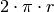 . Damit ergibt sich in
diesem Fall:
. Damit ergibt sich in
diesem Fall:
(16)¶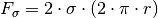
Anhand dieser Formel kann einerseits der „Binnendruck“ in Seifenblasen oder Flüssigkeitstropfen erklärt werden, andererseits lässt sich daraus ebenso eine Formel zur Bestimmung von Tropfengrößen herleiten.
Binnendruck
Betrachtet man eine Seifenblase im Querschnitt, so erkennt man, dass diese aus
aus einer kreisförmigen und sehr dünnen Flüssigkeitsschicht besteht. Sowohl nach
außen wie auch nach innen hin wird die Flüssigkeit durch eine Oberfläche
begrenzt. Im Querschnitt kann der Umfang dieser beiden kreisförmigen Oberflächen
jeweils mit 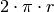 angegeben werden, da die Dicke der
Seifenblasen-Haut gegenüber dem Radius
angegeben werden, da die Dicke der
Seifenblasen-Haut gegenüber dem Radius  der Seifenblase selbst
vernachlässigbar gering ist.
der Seifenblase selbst
vernachlässigbar gering ist.
Die Oberflächenspannung wirkt kontraktiv, sie versucht also die Größe der
Oberfläche zu minimieren; ohne eine weitere Kraft würde die Seifenblase
kollabieren. Tatsächlich ist allerdings Luft in der Seifenblase enthalten, deren
Druck 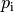 sich bei einer Kompression erhöht. Da dieser Druck
nach außen hin auf die Oberfläche der Seifenblase einwirkt, stellt sich ein
Gleichgewicht zwischen der durch den Druck auf die Oberfläche ausgeübten Kraft
sich bei einer Kompression erhöht. Da dieser Druck
nach außen hin auf die Oberfläche der Seifenblase einwirkt, stellt sich ein
Gleichgewicht zwischen der durch den Druck auf die Oberfläche ausgeübten Kraft
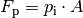 und der durch die
Oberflächenspannung hervorgerufenen kontraktiven Kraft
und der durch die
Oberflächenspannung hervorgerufenen kontraktiven Kraft
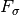 ein:
ein:
![p_{\mathrm{i}} \cdot A &= 2 \cdot \sigma \cdot (2 \cdot \pi \cdot r) \\[6pt]
p_{\mathrm{i}} &= \frac{2 \cdot \sigma \cdot (2 \cdot \pi \cdot r)}{A} \\
&= \frac{4 \cdot \pi \cdot \sigma \cdot r}{\pi \cdot r^2} \\[4pt]
&= \frac{4 \cdot \sigma}{r} \\](../../_images/math/1cea263b62ed39be5d2cc10e68f1cae798733502.png)
Der Druck 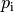 wird als „Binnendruck“ der Seifenblase
bezeichnet; er gibt an, um wie viel größer der Druck der eingeschlossenen Luft
gegenüber der Umgebungsluft ist. Der Binnendruck nimmt, wie sich aus der obigen
Formel erkennen lässt, mit zunehmendem Radius ab. In großen Seifenblasen
herrscht folglich ein kleinerer Binnendruck als in kleinen; treffen zwei
Seifenblasen so aufeinander, dass ein Druckausgleich zwischen den
eingeschlossenen Gasen möglich ist, so strömt die eingeschlossene Luft von der
kleineren zur größeren Blase.
wird als „Binnendruck“ der Seifenblase
bezeichnet; er gibt an, um wie viel größer der Druck der eingeschlossenen Luft
gegenüber der Umgebungsluft ist. Der Binnendruck nimmt, wie sich aus der obigen
Formel erkennen lässt, mit zunehmendem Radius ab. In großen Seifenblasen
herrscht folglich ein kleinerer Binnendruck als in kleinen; treffen zwei
Seifenblasen so aufeinander, dass ein Druckausgleich zwischen den
eingeschlossenen Gasen möglich ist, so strömt die eingeschlossene Luft von der
kleineren zur größeren Blase.
Für Flüssigkeitstropfen oder Luftblasen in einer Flüssigkeit gilt das gleiche Prinzip; da diese jedoch nur eine Oberfläche haben, ist der Binnendruck eines Tropfens nur halb so groß.
Beispiel:
Wie groß ist der Binnendruck
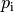 in einem Wassertropfen mit
einem Radius von
in einem Wassertropfen mit
einem Radius von ![\unit[1]{mm}](../../_images/math/d96fa97c6d890bf9efd0b11602b0de8767afb6d5.png) ?
?Für den Binnendruck im Wassertropfen gilt mit
![\sigma_{\mathrm{Wasser}}
\approx \unitfrac[0,072]{N}{m}](../../_images/math/9b9c6543d1b7f30e08cee1d4481232cf1b7a1924.png) :
:![p_{\mathrm{i}} = \frac{2 \cdot \sigma}{r} = \frac{2 \cdot
\unit[0,072]{\frac{N}{m}}}{\unit[0,001]{m}} = \unit[144]{Pa}](../../_images/math/35dc26ca3267c4d518105051cf8706b61d27b646.png)
Der Binnenendruck im Tropfen beträgt somit etwa
![\unit[144]{Pa} =
\unit[1,44]{mbar}](../../_images/math/f71e46dde7c51020059f59952f24a5f882c0c756.png) .
.
Arzneitropfen-Formel
Bei Tropf-Pipetten wird ebenfalls die durch die Oberflächenspannung bedingte Haltekraft ausgenutzt. Der untere, runde Glasrand der Pipette übernimmt dabei die Rolle des runden „Bügels“, mit dessen Hilfe die Oberfläche eines runden Tropfens vergrößert werden soll – allerdings wird hierbei nicht der Bügel gegen den Tropfen bewegt, sondern der am Pipettenrand hängende Tropfen bewegt sich aufgrund seiner während des Ausfließ-Vorgangs zunehmenden Gewichtskraft nach unten.
Im Grenzfall ist die durch die Oberflächenspannung bedingte Haltekraft
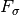 exakt gleich groß wie die Gewichtskraft
exakt gleich groß wie die Gewichtskraft
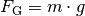 des Tropfens. Als Formel für die Haltekraft
kann auf Gleichung (16) zurückgegriffen werden;
da der Tropfen allerdings nur eine Oberfläche hat, entfällt der Faktor
des Tropfens. Als Formel für die Haltekraft
kann auf Gleichung (16) zurückgegriffen werden;
da der Tropfen allerdings nur eine Oberfläche hat, entfällt der Faktor
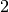 . Es ergibt sich somit:
. Es ergibt sich somit:
![m_{\mathrm{Tropfen}} \cdot g &= \sigma \cdot 2 \cdot \pi \cdot r \\[6pt]
\Rightarrow m_{\mathrm{Tropfen}} &= \frac{2 \cdot \pi \cdot \sigma \cdot
r}{g}](../../_images/math/e46ced71276a7d5e86f4186deb80162234e0ca0b.png)
Die Tropfenmasse ist somit nur durch die Oberflächenspannung  sowie den Radius
sowie den Radius  der Tropf-Pipette festgelegt. Da die
Oberflächenspannung temperaturabhängig ist, muss allerdings mit geringfügigen
Abweichungen vom Sollwert gerechnet werden.
der Tropf-Pipette festgelegt. Da die
Oberflächenspannung temperaturabhängig ist, muss allerdings mit geringfügigen
Abweichungen vom Sollwert gerechnet werden.
Adhäsionskräfte und Benetzbarkeit
Kräfte, die zwischen den Molekülen einer flüssigen und einer festen oder zweier flüssiger beziehungsweise fester Substanzen wirken, bezeichnet man als Adhäsionskräfte. In Flüssigkeiten sind Adhäsionskräfte insbesondere an den Rändern des jeweiligen Gefäßes wirksam.
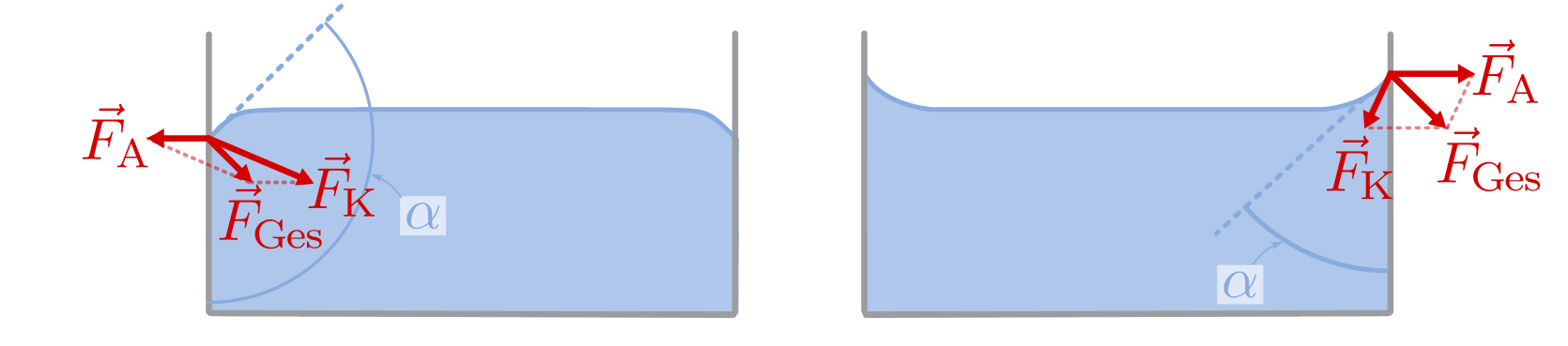
Je nachdem, ob die Kohäsions- oder die Adhäsionskräfte überwiegen, stellt sich zwischen der Gefäßwand und der Oberfläche der Flüssigkeit ein so genannter „Randwinkel“ ein:
- Ist der Randwinkel
 größer als
größer als 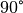 , so überwiegen
die Kohäsionskräfte; die Flüssigkeit ist schlecht benetzend.
, so überwiegen
die Kohäsionskräfte; die Flüssigkeit ist schlecht benetzend. - Ist der Randwinkel
 kleiner als
kleiner als 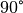 , so
überwiegen die Adhäsionskräfte, und man bezeichnet die Flüssigkeit als
benetzend.
, so
überwiegen die Adhäsionskräfte, und man bezeichnet die Flüssigkeit als
benetzend. - Bei einer ideal benetzenden Flüssigkeit ist
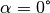 .
.

„Tropfenform“ bei einer schlecht benetzenden, einer gut benetzenden und einer ideal benetzenden Flüssigkeit.
Kapillarität
Je enger ein Gefäß ist, desto deutlicher lassen sich Adhäsionskräfte beobachten.
In sehr engen Röhren („Kapillaren“) kann der Effekt so stark sein, dass das
Flüssigkeitsniveau je nach Benetzbarkeit höher oder niedriger sein kann als es
bei miteinander verbundenen Gefäßen normalerweise der Fall wäre. Beispielsweise
kann Wasser in einer Glasröhre mit einem Radius von ![\unit[1,0]{mm}](../../_images/math/f0d8bb632a09a795d8730dd629b8bf38aa79cfc1.png) bis
zu
bis
zu ![\unit[15]{mm}](../../_images/math/6e89d08a2d9d16d211a80190416fc50ef330081c.png) nach oben gezogen werden, bei einem Radius von nur
nach oben gezogen werden, bei einem Radius von nur
![\unit[0,5]{mm}](../../_images/math/23550a3f97259057b26b349accf5f90b3fe0451a.png) sind sogar Steighöhen von bis zu
sind sogar Steighöhen von bis zu ![\unit[30]{mm}](../../_images/math/ed045d3767f16721558107d186562ea273689b43.png) möglich.
möglich.
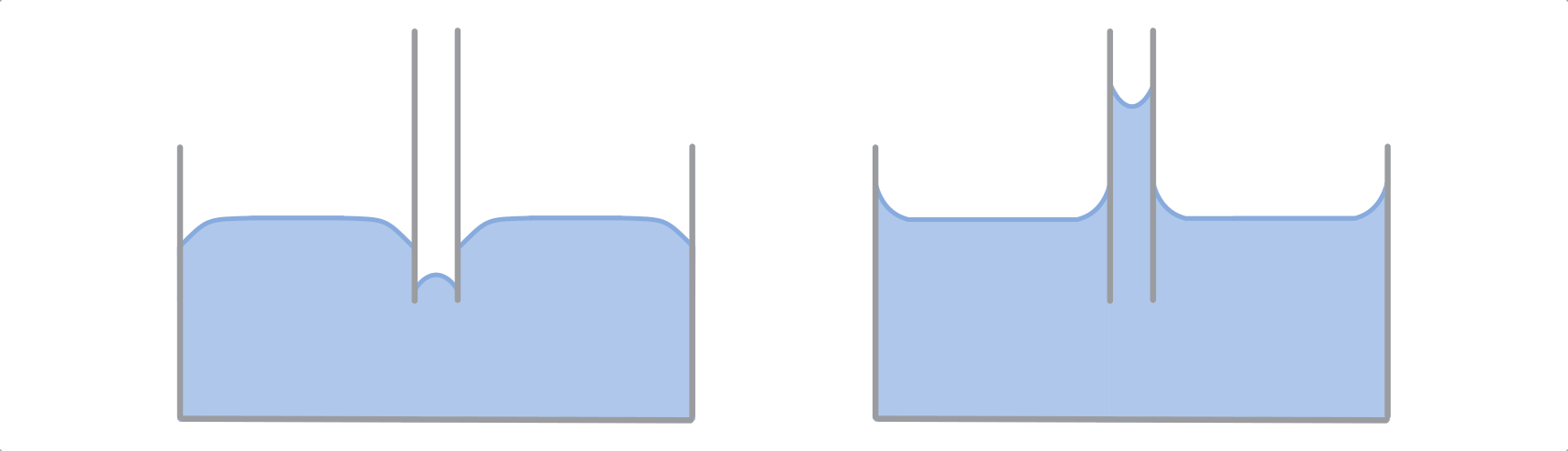
Kapillardepression und Kapillaraszension bei nicht benetzenden beziehungsweise benetzenden Flüssigkeiten.
Bei dieser so genannten „Kapillarität“ herrscht nach der Benetzung der
Randfläche durch die aufsteigende Flüssigkeit – ähnlich wie bei der
Arzneitropfen-Formel – ein Gleichgewicht zwischen der Haltekraft
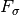 durch die Oberflächenspannung und der Gewichtskraft
durch die Oberflächenspannung und der Gewichtskraft
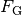 der zusätzlichen, zylinderförmigen Flüssigkeitssäule:
der zusätzlichen, zylinderförmigen Flüssigkeitssäule:
![F_{\mathrm{\sigma}} &= \sigma \cdot 2 \cdot \pi \cdot r \\[4pt]
F_{\mathrm{G}} = \rho _{\mathrm{Fl}} \cdot V_{\mathrm{Fl}} \cdot g &=
\rho_{\mathrm{Fl}} \cdot \pi \cdot r^2 \cdot h \cdot g\\](../../_images/math/d16f2e3275fa3848049afc4f9a7253e3fdb025b1.png)
Setzt man die Terme für diese beiden Kräfte gleich, so erhält man für die
kapillare Steighöhe 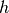 :
:
![\sigma \cdot 2 \cdot \pi \cdot r &= \rho_{\mathrm{Fl}} \cdot \pi \cdot r^2
\cdot h \cdot g \\[4pt]
\Rightarrow h &= \frac{2 \cdot \sigma}{\rho \cdot g \cdot r}](../../_images/math/21794872e503c5b78f40a2e61c2efa236b0d2f84.png)
Bei dieser Herleitung wurde eine ideale Benetzung der Kapillarwand
vorausgesetzt. Eine realistischere Formel für die kapillare Steighöhe erhält
man, wenn man im Zähler des Bruchs durch einen zusätzlichen Faktor
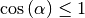 eine gegebenenfalls nicht ideale Benetzbarkeit
berücksichtigt:
eine gegebenenfalls nicht ideale Benetzbarkeit
berücksichtigt:
(17)¶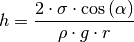
Die maximale Steighöhe ergibt sich genau dann, wenn 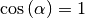 beziehungsweise
beziehungsweise ![\alpha = \unit[0]{\degree}](../../_images/math/ec7da4c6f976f807b80dc58935dba545a0528966.png) ist. Die Flüssigkeit ist in
diesem Grenzfall ideal benetzend und wird somit quasi senkrecht an der Gefäßwand
empor gezogen. Ist bei einer schlechten Benetzung der Randwinkel
ist. Die Flüssigkeit ist in
diesem Grenzfall ideal benetzend und wird somit quasi senkrecht an der Gefäßwand
empor gezogen. Ist bei einer schlechten Benetzung der Randwinkel  hingegen größer als
hingegen größer als ![\unit[90]{\degree}](../../_images/math/ed54e7e9d5b87af841837093aa90f760c14f9678.png) , so ist
, so ist
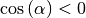 ; man erhält in diesem Fall folglich keine
Kapillaraszension, sondern eine Kapillardepression.
; man erhält in diesem Fall folglich keine
Kapillaraszension, sondern eine Kapillardepression.
Die kapillare Steighöhe ist neben der Oberflächenspannung und der Dichte als Materialkonstanten nur vom Radius der Gefäßröhre abhängig. Die obige Formel kann auch genutzt werden, um aus einer Messung der Steighöhe, des Röhrenradius und des Randwinkels die Oberflächenspannung einer Flüssigkeit zu bestimmen.
Anmerkungen:
| [1] | Das Wasser kann gegebenenfalls sogar „nach hinten losgehen“. Eine derartige Erfahrung hat vermutlich jedes Kind schon einmal gemacht, wenn es versucht hat, mit einem Finger die Öffnung eines Gartenschlauchs abzudichten… ;-) |
| [2] | Da der (Kolben-)Druck in einer ruhenden Flüssigkeit in alle Richtungen gleich groß ist, wird er durch eine skalare Größe angegeben. In Festkörpern wird ein mechanischer Druck stets senkrecht zu einer der Oberflächen angegeben. Die mechanischen Spannungen im Inneren des Festkörpers können in unterschiedlichen Richtungen verschieden groß sein. |
| [3] | Beispielsweise taucht Eis, das eine Dichte von Wird die Dichte in |
| [4] | Der umgangsprachliche Begriff „Staudruck“ sollte nicht verwendet werden,
da er irreführend ist. Beispielsweise müssen die Mauern von Staudämmen
aufgrund des (in alle Richtungen wirkenden) Schweredrucks
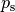 unten dicker sein als oben. Dies gilt auch, wenn sich
das gestaute Wasser nicht bewegt, also kein dynamischer Druck vorliegt. unten dicker sein als oben. Dies gilt auch, wenn sich
das gestaute Wasser nicht bewegt, also kein dynamischer Druck vorliegt. |
| [5] | Beispielsweise beträgt die Viskosität von Glycerin
Ein mathematisches Modell für die Beschreibung der Temperaturabhängigkeit der Viskosität ist folgendes:
Hierbei sind |
| [6] | Manchmal wird in Formelsammlungen und Tabellenwerken auch die so genannte
Fluidität Bisweilen wird auch zwischen der obigen „dynamischen“ Viskosität
|
| [7] | Kohäsionskräfte sind im Wesentlichen in Festkörpern und Flüssigkeiten von Bedeutung. In Gasen lassen sich Kohäsionskräfte nur bei sehr hohem Druck oder sehr tiefen Temperaturen beobachten, da die Abstände der Moleküle ansonsten zu groß und ihre Geschwindigkeiten zu hoch sind. |
Hinweis
Zu diesem Abschnitt gibt es Experimente und Übungsaufgaben.

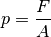
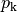 wird die Kraft
wird die Kraft ![\unit[1]{Pa} &= \unit[1]{\frac{N}{m^2}} \\[6pt]](../../_images/math/7ecac4c94f4a59f6390c2edff97ef1b1bad62418.png)
![\unit[1]{bar} &= \unit[100\,000]{Pa}](../../_images/math/bcbe884da202f2e3ba938193e7c83babab165545.png)
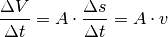
![\unit[20]{\degree C})](../../_images/math/a8fdb99e40d59d21bcbbd3cc109717cbfa5838d2.png)
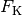 und Addhäsionskraft
und Addhäsionskraft
![\rho_{\mathrm{Eis}}
\approx \unit[910]{\frac{kg}{m^3}}](../../_images/math/1feeeb57bcc3bd2f1fa18ab2552aaa17f8ec76f6.png) hat, zu
hat, zu 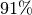 in Wasser (Dichte
in Wasser (Dichte
![\rho_{\mathrm{Fl}} = \unit[1000]{\frac{kg}{m^3}}](../../_images/math/72db8c1799c0ec7910ad2e4a585a74b4347b51aa.png) ) ein, nur die „Spitze
des Eisbergs“ (
) ein, nur die „Spitze
des Eisbergs“ (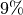 ) bleibt über Wasser sichtbar. Styropor hingegen
hat eine Dichte von etwa
) bleibt über Wasser sichtbar. Styropor hingegen
hat eine Dichte von etwa ![\rho \approx \unit[50]{\frac{kg}{m^3}}](../../_images/math/221c5351a89b25b5763325f8daea62c728fdc3f3.png) ; es
taucht somit nur zu
; es
taucht somit nur zu ![\frac{\rho_{\mathrm{K}}}{\rho_{\mathrm{Fl}}} =
\frac{\unit[50]{\frac{kg}{m^3}}}{\unit[1000]{\frac{kg}{m^3}}} = 0,05 = 5\%](../../_images/math/e34ef7d0019ade0daed290e198c11c717ef645ee.png) in Wasser ein;
in Wasser ein; 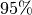 des Styropors schwimmen oberhalb der
Wasseroberfläche.
des Styropors schwimmen oberhalb der
Wasseroberfläche.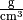 angegeben, so hat Wasser
eine Dichte von
angegeben, so hat Wasser
eine Dichte von ![\unit[1]{\frac{g}{cm^3}}](../../_images/math/bfffe1aa6d6b807d26bdf0f8484f026e7c18432b.png) . In diesem Fall kann man
bei Materialien mit
. In diesem Fall kann man
bei Materialien mit 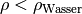 unmittelbar am
Dichtewert den Prozentsatz ablesen, der sich beim Schwimmen unterhalb der
Wasseroberfläche befindet.
unmittelbar am
Dichtewert den Prozentsatz ablesen, der sich beim Schwimmen unterhalb der
Wasseroberfläche befindet.![\unit[12\,100]{mPa \cdot s}](../../_images/math/b077b65c8241475c4325edf9bddec5fe89573820.png) bei einer Temperatur von
bei einer Temperatur von
![\unit[0]{\degree C}](../../_images/math/e8140660503109a1fb799efbf73f7c53ebdd405d.png) . Bei
. Bei ![\unit[1\,480]{mPa \cdot s}](../../_images/math/4b44ba6a868eb2393664f19a16cfce3ebc65f77e.png) , und bei
, und bei
![\unit[624]{mPa \cdot s}](../../_images/math/db221b84a473e48db41eea746b7bebf192b18215.png) .
.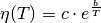
 experimentell zu bestimmende
Konstanten. Die Gleichung kann dann genutzt werden, um Viskositätswerte bei
anderen Temperaturen zu interpolieren.
experimentell zu bestimmende
Konstanten. Die Gleichung kann dann genutzt werden, um Viskositätswerte bei
anderen Temperaturen zu interpolieren.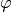 einer Flüssigkeit oder eines Gases angegeben.
Diese ist gleich dem Kehrwert der Fluidität, es gilt also
einer Flüssigkeit oder eines Gases angegeben.
Diese ist gleich dem Kehrwert der Fluidität, es gilt also 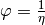 .
.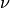 unterschieden. Letztere erhält man, indem man die dynamische Viskosität
durch die Dichte
unterschieden. Letztere erhält man, indem man die dynamische Viskosität
durch die Dichte