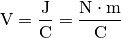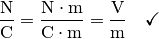Elektrische Felder¶
In ähnlicher Weise wie man das magnetische Feld eines Permanent- oder Elektromagneten zur Beschreibung der Kraftwirkung auf einen anderen Magneten nutzen kann, ist es auch möglich, das elektrische Feld einer Ladungsverteilung zur Beschreibung der Kraftwirkung auf andere elektrische Ladungen zu verwenden. Anders als Magnetfelder verlaufen elektrische Felder jedoch nicht auf geschlossenen Linien, sondern verlaufen von positiven elektrischen Ladungen hin zu negativen Ladungen.
Das Coulombsche Kraftgesetz
Die Grundlage für die Einführung eines elektrischen Felds bildet das so
genannte Colulomb-Gesetz, das
besagt, dass die Kraft zwischen zwei punktförmigen Ladungen proportional zu
Ladungsmengen 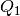 und
und 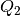 sowie indirekt proportional zum
Quadrat des Abstands
sowie indirekt proportional zum
Quadrat des Abstands  beider Ladungen ist:
beider Ladungen ist:
(1)¶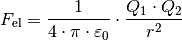
Hierbei ist ![\varepsilon_0 = \unit[8,854 \cdot 10 ^{-12}]{\frac{A \cdot
s}{V \cdot m}}](../_images/math/af3c86dfce90eaf216a357a495a28a1f54490ebd.png) die elektrische Feldkonstante des Vakuums. Die Einheit dieser
wichtigen Naturkonstanten kann wegen
die elektrische Feldkonstante des Vakuums. Die Einheit dieser
wichtigen Naturkonstanten kann wegen ![\unit[1]{V} = \unit[1]{\frac{J}{C}}
=](../_images/math/353bb74c4cb9ac50296e826aa72255de123ce497.png) auch folgendermaßen geschrieben werden:
auch folgendermaßen geschrieben werden:
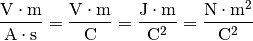
Mit Hilfe der elektrischen Feldkonstanten kann bei bekannten Ladungsmengen und
ihrem Abstand auf die Größe der wirkenden Kraft geschlossen werden; der gesamte
Vorfaktor ![\frac{1}{4 \cdot \pi \cdot \varepsilon_0} \approx \unit[8,99
\cdot 10^9]{\frac{N \cdot m^2}{C^2}}](../_images/math/dbf701babdf3a8f8ad094f3533afb999c19d7396.png) wird bisweilen auch als
„Coulomb-Konstante“ bezeichnet. Anschaulich bedeutet der Wert dieser Konstante,
dass zwei Ladungen von je einem Coulomb, die sich in einem Abstand von einem
Meter zueinander befinden, aufeinander eine Kraft von etwa
wird bisweilen auch als
„Coulomb-Konstante“ bezeichnet. Anschaulich bedeutet der Wert dieser Konstante,
dass zwei Ladungen von je einem Coulomb, die sich in einem Abstand von einem
Meter zueinander befinden, aufeinander eine Kraft von etwa ![\unit[9]{GN}](../_images/math/cf38ba439e727daece9046bd5ac3741d4ac7dbdb.png) ausüben würden – das entspräche einer Gewichtskraft von etwa
ausüben würden – das entspräche einer Gewichtskraft von etwa ![\unit[10
^6]{Tonnen}](../_images/math/acdc505fec9595ae48a39c26de0105b1c8e116e1.png) . Man erkennt an diesem Beispiel zum einen, dass bei vielen
Prozessen, etwa bei sich bewegenden Elektronen, die Gewichtskraft gegenüber der
Coulomb-Kraft meist völlig vernachlässigt werden kann. Andererseits zeigt sich,
dass 1 Coulomb eine sehr große Ladungsmenge darstellt; im Alltag treten
üblicherweise nur Bruchteile dieser Ladungsmenge auf.
. Man erkennt an diesem Beispiel zum einen, dass bei vielen
Prozessen, etwa bei sich bewegenden Elektronen, die Gewichtskraft gegenüber der
Coulomb-Kraft meist völlig vernachlässigt werden kann. Andererseits zeigt sich,
dass 1 Coulomb eine sehr große Ladungsmenge darstellt; im Alltag treten
üblicherweise nur Bruchteile dieser Ladungsmenge auf.
Für die Richtung der wirkenden Coulomb-Kraft gilt:
- Sind die Vorzeichen beider Ladungen gleich, so ist die wirkende Kraft positiv, und die Ladungen stoßen sich ab.
- Haben beide Ladungen hingegen unterschiedliche Vorzeichen, so ist die Coulomb-Kraft negativ, und die Ladungen ziehen einander an.
Sind mehrere Ladungen räumlich getrennt angeordnet, so kann man zunächst die Coulomb-Kräfte paarweise berechnen und anschließend die wirkenden Gesamt-Kräfte durch Addition der Teilkräfte ermitteln.
Elektrische Feldstärke¶
Liegt eine kontinuierliche Verteilung vieler einzelner Ladungen vor, so wäre es
zumindest sehr mühsam, die resultierende Wirkung auf eine weitere Probeladung
als Überlagerung der zahlreichen einzelnen Coulomb-Kräfte zu beschreiben.
Stattdessen verwendet man den Begriff der elektrischen Feldstärke
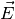 ; diese gibt an, welche Kraftwirkung
; diese gibt an, welche Kraftwirkung
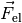 eine Probeladung
eine Probeladung 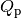 durch eine
bereits vorhandene Ladung oder Ladungsverteilung erfährt:
durch eine
bereits vorhandene Ladung oder Ladungsverteilung erfährt:
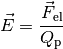
Die elektrische Feldstärke wird in der Einheit 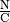 angegeben.[1] Als Vektor gibt die elektrische Feldstärke die Richtung der Kraft an,
die auf eine positive Probeladung wirkt. Die einzelnen Feldlinien gehen deshalb
senkrecht von positiven Ladungen aus und enden senkrecht auf negativen Ladungen.
Die Dichte der Feldlinien kann als Maß für die Stärke des elektrischen Felds
angesehen werden.
angegeben.[1] Als Vektor gibt die elektrische Feldstärke die Richtung der Kraft an,
die auf eine positive Probeladung wirkt. Die einzelnen Feldlinien gehen deshalb
senkrecht von positiven Ladungen aus und enden senkrecht auf negativen Ladungen.
Die Dichte der Feldlinien kann als Maß für die Stärke des elektrischen Felds
angesehen werden.
Die Kraftwirkung auf negative Probeladungen ergibt sich, indem man sich die Pfeilrichtung der Feldlinien vertauscht vorstellt.
Elektrisches Feld eines Plattenkondensators¶
Ein elektrisches Feld mit gleichmäßig verteilten und in die gleiche Richtung zeigenden Feldlinien erhält man, wenn man zwei metallische, zueinander parallel angeordnete Platten mit entgegengesetzten Ladungsträgern bestückt. Im Inneren eines solchen „Plattenkondensators“ ist die elektrische Feldstärke an allen stellen gleich („homogen“).[2]
Der Betrag der elektrischen Feldstärke eines Plattenkondensators ist davon
abhängig, wie viele zusätzliche Ladungen sich über den Plattenflächen
befinden. Das Verhältnis aus der gespeicherten Ladungsmenge 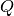 und der
Plattenfläche
und der
Plattenfläche  wird auch als „elektrische Flussdichte“
wird auch als „elektrische Flussdichte“ 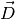 bezeichnet. Für ihren Betrag gilt:
bezeichnet. Für ihren Betrag gilt:
(2)¶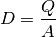
Die elektrische Flussdichte 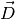 steht, wie auch die elektrische
Feldstärke
steht, wie auch die elektrische
Feldstärke 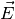 , senkrecht zu den Kondensatorplatten. Der
Zusammenhang zwischen der elektrischen Flussdichte
, senkrecht zu den Kondensatorplatten. Der
Zusammenhang zwischen der elektrischen Flussdichte 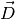 , welche die
Ladungsverteilung beschreibt, und der elektrischen Feldstärke
, welche die
Ladungsverteilung beschreibt, und der elektrischen Feldstärke 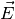 ,
welche die Kraftwirkung auf geladene Teilchen angibt, kann wiederum mittels der
elektrischen Feldkonstante
,
welche die Kraftwirkung auf geladene Teilchen angibt, kann wiederum mittels der
elektrischen Feldkonstante 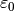 formuliert werden:
formuliert werden:
(3)¶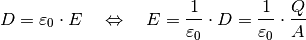
Um einen noch einfacheren Ausdruck für die Elektrische Feldstärke herzuleiten,
ist ein kurzes Gedankenexperiment hilfreich: Wird ein einzelne positive
Probeladung 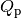 entgegen den Feldlinien von der negativen zur
positiv geladenen Platte verschoben, so muss dafür eine Arbeit
entgegen den Feldlinien von der negativen zur
positiv geladenen Platte verschoben, so muss dafür eine Arbeit 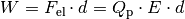 verrichtet werden, wobei
verrichtet werden, wobei
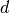 den Plattenabstand bezeichnet. Befindet sich die Ladung anschließend
an der positiven Seite, so besitzt sie eine ebenso große potentielle Energie
den Plattenabstand bezeichnet. Befindet sich die Ladung anschließend
an der positiven Seite, so besitzt sie eine ebenso große potentielle Energie
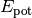 . Als elektrische Spannung
. Als elektrische Spannung  bezeichnet man eben
diese potentielle Energie gegenüber der negativen Plattenseite, bezogen auf die
Größe
bezeichnet man eben
diese potentielle Energie gegenüber der negativen Plattenseite, bezogen auf die
Größe 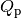 der Probeladung:
der Probeladung:
(4)¶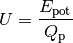
Setzt man 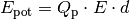 in die obige
Formel ein, so ergibt sich für das elektrische Feld
in die obige
Formel ein, so ergibt sich für das elektrische Feld 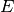 eines
Plattenkondensators folgender nützlicher Zusammenhang:
eines
Plattenkondensators folgender nützlicher Zusammenhang:
(5)¶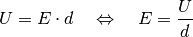
Da sowohl die elektrische Spannung  als auch der Abstand
als auch der Abstand 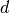 zwischen den geladenen Platten leicht messbare Größen sind, kann das elektrische
Feld eines Plattenkondensators sehr einfach bestimmt werden.
zwischen den geladenen Platten leicht messbare Größen sind, kann das elektrische
Feld eines Plattenkondensators sehr einfach bestimmt werden.
Während das elektrische Feld an allen Stellen im Plattenkondensator gleich ist, nimmt die elektrische Spannung im Kondensator von der positiven zur negativen Platte linear auf Null ab.
Elektrische Influenz und Faradayischer Käfig¶
In Metallen gibt es stets eine Vielzahl an frei beweglicher Elektronen. Im neutralen Zustand werden die negativen Ladungen der Elektronen durch die positiven Ladungen der Atomrümpfe ausgeglichen. Lädt man ein einzelnes Stück Metall mit weiteren Elektronen auf, so verteilen sich diese ausschließlich entlang der Oberfläche, da die zusätzlichen Elektronen ebenfalls frei beweglich sind und sich gegenseitig abstoßen.
Bringt am ein Stück Metall in ein elektrisches Feld ein, so bewirkt dieses eine Verschiebung der frei beweglichen Elektronen zur positiven Platte hin; an der zur negativen Platte hin orientierten Seite bleiben die positiv geladenen Atomrümpfe übrig. Dieser als „elektrische Influenz“ bezeichnete Effekt hält so lange an, bis sich im Metall durch die Ladungsverschiebung ein gleich starkes, aber entgegengesetzt gerichtetes Feld einstellt.
Im Inneren des Metalls überlagern sich das äußere und das induzierte elektrische Feld. Da beide Felder gleich groß, aber entgegengesetzt gerichtet sind, bleibt das Innere des Metalls somit feldfrei. Dies gilt nicht nur massive metallische Körper, sondern auch für metallische Hohlkörper. In der Technik stellen beispielsweise Autokarosserien so genannte „Faradayische Käfige“ dar (benannt nach Michael Faraday), welche die Insassen vor elektrischen Feldern und damit auch vor Stromflüssen, beispielsweise Blitzen, schützen.
Orientierungspolarisation¶
Befinden sich zwei Ladungen mit unterschiedlichem Vorzeichen, aber gleich
großer Ladungsmenge 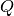 im Abstand
im Abstand  zueinander, so spricht man
von einem elektrischen Dipol. Ein solcher Dipol besitzt ein so genanntes
Dipolmoment
zueinander, so spricht man
von einem elektrischen Dipol. Ein solcher Dipol besitzt ein so genanntes
Dipolmoment 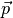 , das proportional zur Ladungsmenge und zum Abstand
der Ladungen ist und in Richtung der positiven Ladung zeigt:
, das proportional zur Ladungsmenge und zum Abstand
der Ladungen ist und in Richtung der positiven Ladung zeigt:
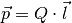
Die Einheit des Dipolmoments ist 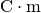 .
.
In der Realität existieren elektrische Dipole in Form von bestimmten Molekülen, die ein permanentes Dipolmoment besitzen, beispielsweise Wasser.
Bringt man einen elektrischen Dipol in ein homogenes elektrisches Feld ein, so
richtet er sich parallel zur Feldrichtung aus. Für das dabei wirkende
Drehmoment 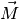 gilt:
gilt:
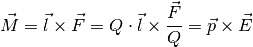
Das Drehmoment ist maximal, wenn der elektrische Dipol senkrecht zu den elektrischen Feldlinien ausgerichtet ist, und wird gleich Null, wenn beide Richtungen identisch sind.
Die Ausrichtung von elektrischen Dipolen durch elektrische Felder wird als Orientierungspolarisation bezeichnet. In realen Anwendungen verhindert die statistisch gleichmäßig verteilte Wärmebewegung der Teilchen eine vollständig Ausrichtung der Dipole; bei abnehmender Temperatur nimmt die Orientierungspolarisation daher zu. Bei Abschalten des elektrischen Felds verschwindet die Orientierungspolarisation wieder.
Verschiebunspolarisation und Dielektrikum¶
Bringt man ein nichtleitendes Material („Dielektrikum“) ohne elektrische Dipole in ein homogenes elektrisches Feld ein, so werden die Ladungsschwerpunkte in allen Atomen leicht verschoben, jeder Atomkern gerät etwas aus dem Zentrum seiner Elektronenhülle. Alle Atome werden somit zu elektrischen Dipolen, auch wenn sie ursprünglich keinen Dipolcharakter besessen haben. Diese Form der Polarisation wird Verschiebungspolarisation genannt.
Bei beiden Polarisationsformen erzeugen die Dipole im Dielektrikum selbst ein
vergleichsweise schwaches und dem äußeren Feld entgegengesetzt gerichtetes
elektrisches Feld. Füllt das Dielektrikum den gesamten Bereich zwischen den
Kondensatorplatten aus, so wird der Wert der elektrischen Feldstärke
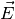 gegenüber dem ursprünglichen Wert um einen Faktor
gegenüber dem ursprünglichen Wert um einen Faktor
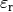 gesenkt. Für einen Plattenkondensator mit
Dielektrikum gilt also allgemein:
gesenkt. Für einen Plattenkondensator mit
Dielektrikum gilt also allgemein:
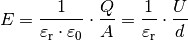
Der Zahlenwert 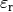 ist eine Materialkonstante, die als
relative Dielektrizitätszahl bezeichnet wird. Streng genommen muss bereits Luft
als Dielektrikum angesehen werden, ihr Wert ist jedoch nur geringfügig von der
Dielektrizitätszahl des Vakuums.
ist eine Materialkonstante, die als
relative Dielektrizitätszahl bezeichnet wird. Streng genommen muss bereits Luft
als Dielektrikum angesehen werden, ihr Wert ist jedoch nur geringfügig von der
Dielektrizitätszahl des Vakuums.
| Material | Dielektrizitätszahl 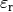 |
| Erde (feucht) | 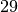 |
| Erde (trocken) | 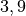 |
| Glas | 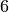 bis bis 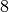 |
| Glimmer | 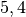 |
| Gummi | 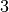 |
| Glycerin | 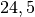 |
| Holz (trocken) | 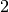 bis bis 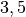 |
| Luft | 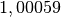 |
| Porzellan | 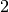 bis bis 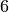 |
| Wasser | 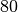 |
Wird ein Kondensator durch eine an die Platten angeschlossene Stromquelle
aufgeladen, so erfolgt dies so lange, bis die elektrische Spannung  zwischen den Kondensator-Platten genauso groß ist wie die anliegende äußere
Spannung. Durch ein Einbringen eines Dielektrikum wird allerdings das
elektrische Feld und somit auch die Spannung zwischen den Kondensator-Platten
gesenkt; somit fließt weitere Ladung auf die Kondensatorplatten nach, bis erneut
die Spannung innerhalb des Kondensators (mit Dielektrikum) so groß ist wie die
anliegende äußere Spannung. Ein Plattenkondensator kann also mit Dielektrikum
eine größere Ladungsmenge speichern als ohne.
zwischen den Kondensator-Platten genauso groß ist wie die anliegende äußere
Spannung. Durch ein Einbringen eines Dielektrikum wird allerdings das
elektrische Feld und somit auch die Spannung zwischen den Kondensator-Platten
gesenkt; somit fließt weitere Ladung auf die Kondensatorplatten nach, bis erneut
die Spannung innerhalb des Kondensators (mit Dielektrikum) so groß ist wie die
anliegende äußere Spannung. Ein Plattenkondensator kann also mit Dielektrikum
eine größere Ladungsmenge speichern als ohne.
Kapazität eines Plattenkondensators¶
Die Kapazität eines Plattenkondensators gibt an, wie viel die Ladungsmenge
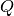 ist, die der Kondensator bei einer anliegenden Spannung
ist, die der Kondensator bei einer anliegenden Spannung  insgesamt aufnehmen kann:
insgesamt aufnehmen kann:
(6)¶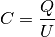
Die Einheit der Kapazität ist Farad ![(\unit[1]{F} =
\frac{\unit[1]{C}}{\unit[1]{V}})](../_images/math/41f5969b64b4b8b25348183ee344b871e67697ae.png) . Da ein Coulomb eine sehr große Ladungsmenge
darstellt, ist ebenso eine Kapazitätsmenge von einem Farad sehr groß. In der
Praxis übliche Kondensatoren werden daher in Pikofarad
. Da ein Coulomb eine sehr große Ladungsmenge
darstellt, ist ebenso eine Kapazitätsmenge von einem Farad sehr groß. In der
Praxis übliche Kondensatoren werden daher in Pikofarad 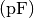 ,
,
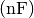 oder Mikrofarad
oder Mikrofarad 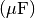 angegeben.
angegeben.
Die obige Formel (6) gilt allgemein für alle Bauarten von
Kondensatoren. Bei einem Plattenkondensator ist die
Kapazität abhängig von der Fläche  der beiden Kondensatorplatten, von
ihrem Abstand
der beiden Kondensatorplatten, von
ihrem Abstand 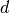 sowie vom Dielektrikum, das sich zwischen den beiden
Kondensatorplatten befindet. Handelt es sich beim Dielektrikum um Vakuum oder
Luft, so gilt für die Kapazität
sowie vom Dielektrikum, das sich zwischen den beiden
Kondensatorplatten befindet. Handelt es sich beim Dielektrikum um Vakuum oder
Luft, so gilt für die Kapazität 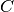 des Plattenkondensators:
des Plattenkondensators:
(7)¶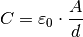
Hierbei bezeichnet ![\varepsilon_0= \unit[8,854 \cdot 10 ^{-12}]{\frac{A
\cdot s}{V \cdot m}}](../_images/math/c0d0beed54b4aa9be5f904bbe5140f75f07b4381.png) wiederum die elektrische Feldkonstante. Handelt es sich
beim Dielektrikum um ein anderes Material, so muss anstelle von
wiederum die elektrische Feldkonstante. Handelt es sich
beim Dielektrikum um ein anderes Material, so muss anstelle von
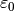 der Wert
der Wert 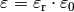 in die obige Gleichung eingesetzt werden, wobei
in die obige Gleichung eingesetzt werden, wobei
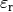 die Dielektrizitätszahl des jeweiligen Materials ist. Durch ein geeignetes
Dielektrikum zwischen den Kondensatorplatten kann somit die Kapazität des
Kondensators bei gleicher Baugröße um ein Vielfaches erhöht werden.
die Dielektrizitätszahl des jeweiligen Materials ist. Durch ein geeignetes
Dielektrikum zwischen den Kondensatorplatten kann somit die Kapazität des
Kondensators bei gleicher Baugröße um ein Vielfaches erhöht werden.
Elektrische Energie in einem Plattenkondensator
Wird in einem Plattenkondensator eine Ladung positive Ladung 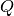 entgegen
der elektrischen Feldlinien bewegt, so muss Arbeit gegen die elektrische Kraft
entgegen
der elektrischen Feldlinien bewegt, so muss Arbeit gegen die elektrische Kraft
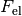 verrichtet werden. Bewegt man die Ladung von der
negativen zur positiven Platte, die voneinander den Plattenabstand
verrichtet werden. Bewegt man die Ladung von der
negativen zur positiven Platte, die voneinander den Plattenabstand 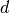 haben, so gilt für die verrichtete Arbeit
haben, so gilt für die verrichtete Arbeit 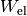 :
:
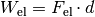
Wird ein Kondensator geladen, so kann man sich die dabei verrichtete elektrische Arbeit als schrittweisen Transport von elektrischer Ladung von einer Kondensatorplatte zur anderen vorstellen – nicht über die Luft zwischen den Kondensatorplatten, aber über die Anschlussdrähte. Als Folge der Ladungstrennung baut sich im Kondensator zunehmend eine elektrische Spannung auf.
Hat die Spannung zwischen den Kondensatorplatten den Wert  , so musste
während des Ladevorgangs schrittweise Spannungen zwischen Null und
, so musste
während des Ladevorgangs schrittweise Spannungen zwischen Null und  überwunden werden; die durchschnittliche Ladespannung hat also
überwunden werden; die durchschnittliche Ladespannung hat also 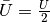 betragen.
betragen.
Mit 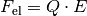 und
und 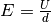 ergibt sich:
ergibt sich:
![W_{\mathrm{el}} = \bar{F}_{\mathrm{el}} \cdot d &= Q \cdot \bar{E} \cdot d
\\[8pt]
&= Q \cdot \frac{\bar{U}}{d} \cdot d = Q \cdot \bar{U} = \frac{1}{2} \cdot Q
\cdot U](../_images/math/6cc91587b67b59ca933a65da9c217b5f09aa961c.png)
Schreibt man zusätzlich 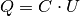 , so erhält man für die insgesamt
während des Ladens verrichtete elektrische Arbeit:
, so erhält man für die insgesamt
während des Ladens verrichtete elektrische Arbeit:
(8)¶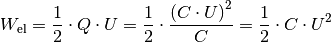
Diese Arbeitsmenge bleibt in Form von elektrischer Energie im Kondensator gespeichert.
Das Millikan-Experiment¶
Im Jahr 1910 konnte Robert Millikan erstmals mittels eines
Plattenkondensators die Größe der Elementarladung  experimentell
bestimmen. Die Grundidee seines Experiments war es, mittels eines Zerstäubers
winzige, durch Reibungseffekte zumindest teilweise elektrisch geladene
Öltröpfchen zwischen die Platten des Kondensators zu bringen.
experimentell
bestimmen. Die Grundidee seines Experiments war es, mittels eines Zerstäubers
winzige, durch Reibungseffekte zumindest teilweise elektrisch geladene
Öltröpfchen zwischen die Platten des Kondensators zu bringen.
Liegt am Kondensator keine elektrische Spannung an, so sinken die Tröpfchen
aufgrund ihrer Gewichtskraft 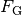 langsam nach unten; aufgrund
der kleinen Tröpfchengröße sind hierbei die statische Auftriebskraft
langsam nach unten; aufgrund
der kleinen Tröpfchengröße sind hierbei die statische Auftriebskraft
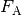 der Tröpfchen in Luft sowie die Reibungskraft
der Tröpfchen in Luft sowie die Reibungskraft
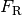 nicht zu vernachlässigen.
nicht zu vernachlässigen.
Wird hingegen ein elektrisches Feld angelegt, so kann die (nur auf elektrisch
geladene Öltröpfchen) wirkende elektrische Kraft 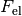 die
Gewichtskraft ausgleichen; bei einer ausreichend großen elektrischen Spannung
können die geladenen Teilchen sogar wieder nach oben steigen.
die
Gewichtskraft ausgleichen; bei einer ausreichend großen elektrischen Spannung
können die geladenen Teilchen sogar wieder nach oben steigen.
Für die wirkenden Kräfte gilt:
![F_{\mathrm{G}} &= m_{\text{\"Ol}} \cdot g = \rho_{\text{Öl}} \cdot V \cdot g
\\[4pt]
F_{\mathrm{A}} &= \; m_{\mathrm{L}} \cdot g = \; \rho_{\mathrm{L}} \cdot V
\cdot g \\[8pt]
F_{\mathrm{el}} &= Q \cdot E = Q \cdot \frac{U}{d}](../_images/math/4a6f8469a76bd53046e560af6d6480aa341c0779.png)
Hierbei bezeichnet ![g = \unit[9,81]{\frac{N}{kg}}](../_images/math/b110fbd8a63b132b1c9db4716ab6f929f5d8ecbc.png) den Ortsfaktor,
den Ortsfaktor,
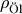 die Dichte des Öls und
die Dichte des Öls und 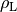 die
Dichte der Luft. Für das Volumen der kugelförmigen Öltröpfchen gilt
die
Dichte der Luft. Für das Volumen der kugelförmigen Öltröpfchen gilt
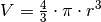 , wobei
, wobei  den Radius der
Öltröpfchen angibt.
den Radius der
Öltröpfchen angibt.
Schweben die Öltröpfchen in der Luft, so muss folgendes Gleichgewicht gelten:
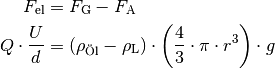
Für die Ladung 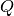 eines schwebenden Öltröpfchens muss somit gelten:
eines schwebenden Öltröpfchens muss somit gelten:
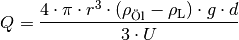
In dieser Gleichung sind, abgesehen vom Radius  der Öltröpfchen, alle
Größen konstant oder leicht messbar. Die größte Schwierigkeit besteht im exakten
Messen des Radius
der Öltröpfchen, alle
Größen konstant oder leicht messbar. Die größte Schwierigkeit besteht im exakten
Messen des Radius  (durch die Brownsche Molekularbewegung noch
zusätzlich erschwert), wobei Messfehler durch die dritte Potenz einen
erheblichen Einfluss auf das Ergebnis haben können. Millikan bestimmte daher
zusätzlich die Geschwindigkeiten einzelner Tröpfchen beim Sinken, was er durch
ein zwischenzeitliches Abschalten der anliegenden Spannung erreichte.
(durch die Brownsche Molekularbewegung noch
zusätzlich erschwert), wobei Messfehler durch die dritte Potenz einen
erheblichen Einfluss auf das Ergebnis haben können. Millikan bestimmte daher
zusätzlich die Geschwindigkeiten einzelner Tröpfchen beim Sinken, was er durch
ein zwischenzeitliches Abschalten der anliegenden Spannung erreichte.
Erreichen die Tröpfchen beim Sinken eine konstante Geschwindigkeit  , so
gilt folgendes Kräftegleichgewicht:
, so
gilt folgendes Kräftegleichgewicht:
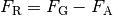
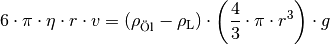
In der obigen Gleichung bezeichnet 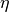 die Viskosität der Luft; bei
die Viskosität der Luft; bei ![\unit[20]{\degree C}](../_images/math/5306d44af8f7df91464b32ed64cda4ded46190b0.png) beträgt diese
beträgt diese
![\eta \approx \unit[0,0182]{mPa \cdot s}](../_images/math/79eeeb965c3e7a1ceb46950d72c39e6a47fbdb3e.png) . Löst man die Gleichung nach
. Löst man die Gleichung nach
 auf, so erhält man:
auf, so erhält man:
![6 \cdot \eta \cdot v &= (\rho_{\text{Öl}} - \rho_{\mathrm{L}}) \cdot
\frac{4}{3} \cdot g \cdot r^2 \\[6pt]
r^2 &= \frac{6 \cdot 3 \cdot \eta \cdot v}{4 \cdot g \cdot (\rho_{\text{Öl}}
- \rho_{\mathrm{L}})} \\[6pt]
r &= \sqrt{\frac{9 \cdot \eta \cdot v}{2 \cdot g \cdot (\rho_{\text{Öl}} -
\rho_{\mathrm{L}})}} \\[6pt]](../_images/math/16b6e9f0f343086890b2bd3e9a52c9f9375df244.png)
Durch Messung der Viskosität der Luft und der Sinkgeschwindigkeit  der
Tröpfchen ohne elektrisches Feld kann der Radius
der
Tröpfchen ohne elektrisches Feld kann der Radius  der Tröpfchen mit
guter Genauigkeit bestimmt werden.
der Tröpfchen mit
guter Genauigkeit bestimmt werden.
Millikan stellte fest, dass die sich ergebenden Ladungswerte stets ganzzahlige
Vielfache einer „Elementarladung“ waren. Er bestimmte den Wert dieser Ladung zu
![\unit[1,592 \cdot 10^{-19}]{C}](../_images/math/a82ff61a622ada00a0ee63b73665b03ca77f4a78.png) , was mit dem heute bekannten Wert von
, was mit dem heute bekannten Wert von
![q_{\mathrm{e}}=\unit[1,602 \cdot 10^{-19}]{C}](../_images/math/ba1acc5e0e23eafb5910d9fecaea83236e096b78.png) bereits sehr gut
übereinstimmte.
bereits sehr gut
übereinstimmte.
Bewegung von geladenen Teilchen in elektrischen Feldern¶
Bringt man ein Teilchen mit einer elektrischen Ladung 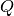 in ein
elektrisches Feld mit einer Feldstärke
in ein
elektrisches Feld mit einer Feldstärke 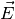 , so erfährt es gemäß
, so erfährt es gemäß
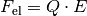 eine Kraftwirkung. Handelt es sich bei dem
Teilchen um ein Elektron oder Proton, so kann die Gewichtskraft des Teilchens
gegenüber der elektrischen Kraft
eine Kraftwirkung. Handelt es sich bei dem
Teilchen um ein Elektron oder Proton, so kann die Gewichtskraft des Teilchens
gegenüber der elektrischen Kraft 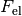 meist vernachlässigt
werden.
meist vernachlässigt
werden.
Für technische Anwendungen ist insbesondere die Bewegung von Elektronen in elektrischen Feldern von Bedeutung.
Bewegung in Richtung des elektrischen Feldes
Angenommen, ein frei bewegliches Elektron befindet sich zunächst in unmittelbarer Nähe der negativ geladenen Seite eines Plattenkondensators. Durch die elektrische Feldstärke wird es dann zur positiven geladenen Seite hin beschleunigt. Diese Bewegung ähnelt dem freien Fall eines Gegenstands im Gravitationsfeld der Erde: Es wird potentielle Energie in kinetische Energie umgewandelt.
Gemäß der Definition der Spannung (4) kann die potentielle Energie des Elektrons folgendermaßen ausgedrückt werden:[3]
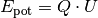
Die potentielle Energie des Elektrons ist also ausschließlich abhängig von der
im Plattenkondensator anliegenden Spannung  , da die Ladung
, da die Ladung
![Q_{\mathrm{el}} = \unit[1,602 \cdot 10^{-19}]{C}](../_images/math/e07d14f27179df80809051377d861ed99c9abd9d.png) des Elektrons konstant
ist.
des Elektrons konstant
ist.
Beispiel:
Liegen an den Platten eines Kondensators
![U=\unit[100]{V}](../_images/math/625155d44c735d34681b040fc8cb7c5735a3aa21.png) an, so ein
Elektron, das sich in unmittelbarer Nähe der negativen Platte befindet,
folgende Energiemenge:
an, so ein
Elektron, das sich in unmittelbarer Nähe der negativen Platte befindet,
folgende Energiemenge:![E_{\mathrm{pot}} = Q_{\mathrm{el}} \cdot U = \unit[1,602 \cdot
10^{-19}]{C} \cdot \unit[100]{V} = \unit[1,602 \cdot 10^{-17}]{J}](../_images/math/1b758fd549b77eaa940c56e869ece11749322597.png)
Die Einheit ergibt sich aus
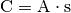 und
und
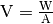 zu
zu 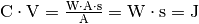 .
.
Da die Energiemengen bei einzelnen Elektronen ziemlich gering sind, ist es
üblich, diese in der Einheit „Elektronenvolt“ anzugeben. Hierbei wird mit
![e \equiv Q_{\mathrm{el}} = \unit[1,602 \cdot 10^{-19}]{C}](../_images/math/09d723ad3c77a2da658fa551ff4df7adc445b562.png) die Ladung
eines einzelnen Elektrons bezeichnet; multipliziert man diesen Wert mit dem Wert
der anliegenden Spannung, so erhält man unmittelbar die Energiemenge in
Elektronenvolt. Für das obige Beispiel würde entsprechend
die Ladung
eines einzelnen Elektrons bezeichnet; multipliziert man diesen Wert mit dem Wert
der anliegenden Spannung, so erhält man unmittelbar die Energiemenge in
Elektronenvolt. Für das obige Beispiel würde entsprechend
![E_{\mathrm{pot}} = 1 \, e \cdot \unit[100]{V} = \unit[100]{eV}](../_images/math/717d87be8817a2f58eb6f3a6aa2eb2ce3bdcf0a0.png) gelten.
gelten.
Erreicht das Elektron die positiv geladene Platte, so ist die gesamte potentielle Energie des Elektrons in kinetische Energie umgewandelt worden. Hierbei muss also gelten:
![E_{\mathrm{kin}} &= E_{\mathrm{pot}} \\[4pt]
\frac{1}{2} \cdot m_{\mathrm{el}} \cdot v^2 &= Q \cdot U \\[4pt]](../_images/math/c07825ed6fb0cae74286a6f1e5d425c1fad40bb7.png)
Das Elektron erreicht somit unmittelbar vor dem Aufprall auf der positiven Leiterplatte folgende Geschwindigkeit:
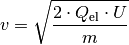
Diese Gleichung kann nicht nur für Elektronen, sondern ebenso für andere geladene Teilchen (beispielsweise Ionen) verwendet werden. Diese tragen meist ebenso nur eine einzelne Elementarladung oder ein geringzahliges Vielfaches davon, haben jedoch eine weitaus höhere Masse; somit ergeben sich wesentlich geringere Geschwindigkeitswerte als bei Elektronen.
Beispiel:
Liegt wie im obigen Beispiel eine Spannung von
![U=\unit[100]{V}](../_images/math/625155d44c735d34681b040fc8cb7c5735a3aa21.png) am
Kondensator an, so ergibt sich mit
am
Kondensator an, so ergibt sich mit ![m_{\mathrm{el}} = \unit[9,1 \cdot
10^{-31}]{kg}](../_images/math/ada504443d32cc5f0699801cd198405236f71f14.png) für ein Elektron folgende Aufprall-Geschwindigkeit:
für ein Elektron folgende Aufprall-Geschwindigkeit:![v = \sqrt{\frac{2 \cdot \unit[1,602 \cdot 10^{-19}]{C} \cdot
\unit[100]{V}}{\unit[9,1 \cdot 10^{-31}]{kg}}} \approx \unit[5,93 \cdot
10^{6}]{\frac{m}{s}}](../_images/math/c1567aebf58afa7bf40db1b40e06c1d29488aefa.png)
Die Einheit ergibt sich aus folgender Beziehung:
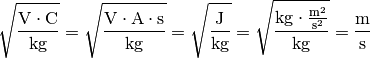
Trotz der scheinbar geringen Energiemenge von
![E_{\mathrm{pot}}=\unit[100]{eV} = \unit[1,602 \cdot 10^{-17}]{J}](../_images/math/570e9ecde04798c462ac9ede67d25c940f1fb6be.png) erreicht das Elektron bereits eine Geschwindigkeit von über
erreicht das Elektron bereits eine Geschwindigkeit von über
![\unit[5]{Mio.\; \frac{m}{s}}](../_images/math/bd4bd532b38d14074ce69152ae2e2eeb3c37f06b.png) ; dies entspricht bereits rund
; dies entspricht bereits rund 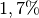 der Lichtgeschwindigkeit.[4] Wird die Spannung, wie beispielsweise in
Braunschen Röhren üblich, um einen Faktor
der Lichtgeschwindigkeit.[4] Wird die Spannung, wie beispielsweise in
Braunschen Röhren üblich, um einen Faktor 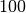 auf
auf
![\unit[10\,000]{V}](../_images/math/c17dd4860cf8f8b0fa26095b74902247010cf717.png) erhöht, so steigt die Geschwindigkeit beim Aufprall um
den Faktor
erhöht, so steigt die Geschwindigkeit beim Aufprall um
den Faktor 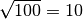 an.
an.
In klassischen Oszilloskopen und Braunschen Röhren werden die freien Elektronen von einem spiralförmig aufgewickelten Heizdraht ausgesendet („Glühelektrischer Effekt“). Ohne ein weiteres wirksames elektrisches Feld würde sich der Draht dabei aufgrund der verbleibenden Atomrümpfe positiv aufladen, und die Elektronen würden zurück in Richtung des Drahtes beschleunigt. Als Folge davon ergäbe sich eine nur wenige Millimeter dicke „Elektronenwolke“ um den Heizdraht herum. Wird hingegen mittels einer (positiv geladenen) Anode ein elektrisches Feld angelegt, so werden die Elektronen entlang der Feldlinien in Richtung der Anode beschleunigt.
Bewegung senkrecht zum elektrischen Feld
Erfolgt die Bewegung eines geladenen Teilchens, beispielsweise eines Elektrons, (zunächst) senkrecht zur Richtung des elektrischen Felds eines Plattenkondensators, so gleicht die vom geladenen Teilchen durchlaufene Bahn derjenigen, die ein waagrecht geworfener Gegenstand im Gravitationsfeld der Erde durchläuft.
Verläuft das elektrische Feld in vertikaler Richtung, so bleibt die horizontale
Komponente der Geschwindigkeit des geladenen Teilchens unverändert. Tritt das
Teilchen zur Zeit 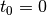 an der Stelle
an der Stelle 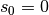 in das
elektrische Feld ein, so muss also gelten:
in das
elektrische Feld ein, so muss also gelten:
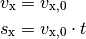
In Vertikaler Richtung hat das geladene Teilchen zunächst eine Geschwindigkeit
von 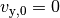 . Tritt das Teilchen mittig (in der Höhe
. Tritt das Teilchen mittig (in der Höhe
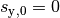 ) in das elektrische Feld ein, so wird es durch das
elektrische Feld konstant beschleunigt. Somit muss gelten:
) in das elektrische Feld ein, so wird es durch das
elektrische Feld konstant beschleunigt. Somit muss gelten:
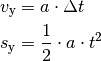
Die Beschleunigung  , die ein geladenes Teilchen im elektrischen Feld
erfährt, kann man wegen
, die ein geladenes Teilchen im elektrischen Feld
erfährt, kann man wegen 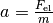 als
als 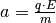 schreiben. Handelt es sich bei dem geladenen Teilchen um
ein freies Elektron, so ist
schreiben. Handelt es sich bei dem geladenen Teilchen um
ein freies Elektron, so ist 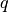 gleich der Elementarladung
gleich der Elementarladung
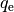 , so ergibt sich:
, so ergibt sich:
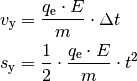
Um die Geschwindigkeit beziehungsweise die Position des Teilchens nicht
in Abhängigkeit von der Zeit, sondern in Abhängigkeit von der horizontalen
Entfernung 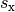 auszudrücken, kann man den Zusammenhang
auszudrücken, kann man den Zusammenhang
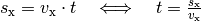 nutzen:
nutzen:
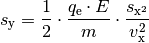
Bei einem Strahl aus freien Elektronen treten diese mit einer jeweils gleichen
Eintrittsgeschwindigkeit 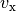 in das elektrische Feld ein.
Durch eine Variation der Spannung an den Kondensatorplatten und damit einer
Beeinflussung des elektrischen Feldes
in das elektrische Feld ein.
Durch eine Variation der Spannung an den Kondensatorplatten und damit einer
Beeinflussung des elektrischen Feldes 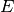 kann somit die Bahn der
Elektronen unmittelbar beeinflusst werden. Dieser Effekt wird beispielsweise in
Röhren-Oszilloskopen genutzt, um den zeitlichen Verlauf eines beziehungsweise
zweier Spannungssignale auf einem Schirm sichtbar zu machen.
kann somit die Bahn der
Elektronen unmittelbar beeinflusst werden. Dieser Effekt wird beispielsweise in
Röhren-Oszilloskopen genutzt, um den zeitlichen Verlauf eines beziehungsweise
zweier Spannungssignale auf einem Schirm sichtbar zu machen.
Anmerkungen:
| [1] | Eine weitere gebräuchliche Einheit für die elektrische Feldstärke ist
Damit lässt sich die Einheit der elektrischen Feldstärke folgendermaßen umformulieren:
|
| [2] | An den Rändern des Kondensators sind die Feldlinien zwar gekrümmt, doch im Inneren verlaufen die Feldlinien nahezu parallel. |
| [3] | Auf den Platten eines geladenen Kondensators befinden sich eine Vielzahl
an Ladungsträgern. Beim obigen Ansatz wird daher angenommen, dass ein
einzelnes Elektron, das von einer Seite des Kondensators auf die andere
gelangt, keinen Einfluss auf die Ladungsverteilung des Kondensators und
somit auf die anliegende Spannung hat. Wird die Spannung im Kondensator
durch eine äußere Spannungsquelle aufrecht erhalten, kann  während
des Vorgangs als konstant angesehen werden. während
des Vorgangs als konstant angesehen werden. |
| [4] | Auch die Bindungsenergien der Elektronen an den Atomkern werden in
Elektronenvolt angegeben. Beispielsweise genügt bei den meisten chemischen
Elementen bereits eine Energiemenge von etwa ![\unit[15]{eV}](../_images/math/bd2ba0e02076089fa8f346959fe4b1902e4c477b.png) , um ein
einzelnes Elektron aus der Atomhülle zu lösen („erste Ionisierungsenergie“). Um
weitere Elektronen aus der Atomhülle zu lösen, sind meist deutlich höhere
Energiemengen erforderlich (siehe folgende Tabelle auf Wikipedia). , um ein
einzelnes Elektron aus der Atomhülle zu lösen („erste Ionisierungsenergie“). Um
weitere Elektronen aus der Atomhülle zu lösen, sind meist deutlich höhere
Energiemengen erforderlich (siehe folgende Tabelle auf Wikipedia). |
Hinweis
Zu diesem Abschnitt gibt es Übungsaufgaben.







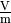 . Der Zusammenhang ergibt sich aus der Definition von der
Einheit Volt:
. Der Zusammenhang ergibt sich aus der Definition von der
Einheit Volt: