Aufgaben zur Mengenlehre¶
Mengenoperationen¶
Die folgenden Aufgaben beziehen sich auf den Abschnitt Mengenoperationen.
(*) Welche Ergebnismenge ergibt sich bei der Bildung der Vereinigungsmenge
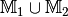, wenn 
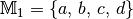und 
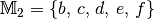ist?
(*) Welche Ergebnismenge ergibt sich bei der Bildung der Schnittmenge zweier Mengen
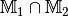, wenn diese folgende Elemente
beinhalten:![\begin{array}{>{\arraybackslash$}p{8cm}<{$} >{\arraybackslash$}p{8cm}<{$}}
\text{a) } \mathbb{M}_1 = \{ 1,\,2,\,3,\,4 \}\; ; &
\text{b) } \mathbb{M}_1 = \{ a,\,b,\,c,\,d \}\; ;\\[4pt]
\phantom{\text{a) }} \mathbb{M}_2 = \{ 2,\,4,\,6,\,8,\,10 \} &
\phantom{\text{b) }} \mathbb{M}_2 = \{ m,\,n,\,o,\,p,\,q \} \\[12pt]
\text{c) } \mathbb{M}_1 = \{ \frac{9}{3},\, 4,\, 5^2 \} \; ; \; \mathbb{M}_2 = \{ 3^3,\, \sqrt{9},\, 7 \}&
\text{d) } \mathbb{M}_1 = \{ x \, | \; x < 5 \} \; ; \; \mathbb{M}_2 = \{ x \, | \; x \ge 3 \}\\[12pt]
\end{array}](../_images/math/1314d855986d380bc1887a7f1ec2eb368e8bd308.png)
(*) Wie lässt sich anhand der beiden Mengen
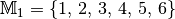und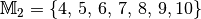 
zeigen, dass bei einer Differenzmenge 
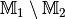die Mengen 
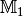und 
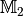im
Allgemeinen nicht vertauscht werden können?
Abbildungen und Funktionen¶
Die folgenden Aufgaben beziehen sich auf den Abschnitt Abbildungen, Funktionen, Relationen und Operationen.
(*) In folgender Abbildung ist eine Abbildung von Elementen der Menge
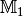auf Elemente der Menge 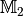dargestellt.
SVG: Venn-Diagramm einer Abbildung (Aufgabe)Wie lässt sich diese Abbildung als Menge darstellen? Kann die Abbildung auch als Funktion aufgefasst werden?
