Integralrechnung¶
Die folgenden Aufgaben beziehen sich auf den Abschnitt Integralrechnung.
Integrationsmethoden
Ein zunächst leeres Waschbecken wird bis zu einem Zeitpunkt von
![t_1 =
\unit[30]{s}](../_images/math/6ab84c82ef893ccf1bd6966d1ec4f9f31d48c22f.png)
mit Wasser gefüllt, wobei der Volumenstrom in diesem Zeitabschnitt konstant ![\dot{V} =
\frac{\Delta V_1}{\Delta t_1} = \unit[0,3]{\frac{l}{s}}](../_images/math/7642e0fcd9b940cbd74afdbe8dd62c7a2bd10e6d.png)
beträgt. Anschließend
wird der Wasserzufluss gestoppt.Ab dem Zeitpunkt
![t_2 = \unit[45]{s}](../_images/math/a06f3a46005336f9ef1054f7b523cfe29bed742e.png)
wird dann der Ablauf des
Waschbeckens geöffnet, wobei das Wasser mit einem konstanten Volumenstrom von
![\dot{V} = \frac{\Delta V_2}{\Delta t_2} = \unit[1,2]{\frac{l}{s}}](../_images/math/77c6c60dbf79b0da14ac7069dffd9de0479b79b6.png)
ausfließt.Wieviel Wasser wird zum Zeitpunkt
![t_3=\unit[50]{s}](../_images/math/8a800da35993c3208f89ebf80d38f4b2d17f2005.png)
noch im Waschbecken
enthalten sein?
Welchen Wert hat das Integral
?
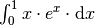