Integralrechnung¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Integralrechnung.
Integrationsmethoden
Bei dieser Aufgabe entspricht die Variable
 der Zeit
der Zeit 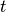 . Dies
kommt bei physikalischen Aufgaben so häufig vor, dass eigens die Notation
. Dies
kommt bei physikalischen Aufgaben so häufig vor, dass eigens die Notation
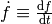 anstelle von
anstelle von  eingeführt wurde.
eingeführt wurde.Da die Zu- beziehungsweise Abflussmenge in den jeweiligen Zeitabschnitten konstant ist, kann die im Waschbecken enthaltene Wassermenge sehr einfach berechnet werden. Hierbei wird folgende Integralregel verwendet:
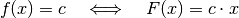
Wendet man diese Regel an (mit
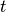 anstelle von
anstelle von  als Variable)
auf den konstanten Volumenstrom
als Variable)
auf den konstanten Volumenstrom 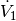 an, so ergibt sich mit
an, so ergibt sich mit
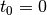 für die im Waschbecken enthaltene Wassermenge am Ende des ersten
Zeitabschnitts:
für die im Waschbecken enthaltene Wassermenge am Ende des ersten
Zeitabschnitts:![\int_{t_0}^{t_1} \dot{V}_1 \cdot \mathrm{d}t = \big( \dot{V}_1 \cdot t
\big) \Big | _{\mathrm{t_1}} ^{t_2} = \dot{V}_1 \cdot t_1 - \dot{V}_1
\cdot t_0 = \unit[0,3]{\frac{l}{s}} \cdot \unit[30]{s} = \unit[9,0]{l}](../_images/math/5616780c8c3c5a097110135e18efcb46510dbada.png)
Der zweite Term
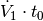 ergibt hierbei den Wert Null, da
ergibt hierbei den Wert Null, da
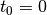 ist. Zum Zeitpunkt
ist. Zum Zeitpunkt 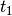 sind somit neun Liter Wasser im
Waschbecken enthalten.
sind somit neun Liter Wasser im
Waschbecken enthalten.Im Zeitraum zwischen
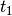 und
und 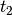 ist der Zu- beziehungsweise
Ablauf verschlossen und somit der fließende Volumenstrom gleich Null. Die im
Zeitraum zwischen
ist der Zu- beziehungsweise
Ablauf verschlossen und somit der fließende Volumenstrom gleich Null. Die im
Zeitraum zwischen 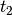 und
und 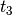 abfließende Wassermenge kann
wiederum nach dem obigen Prinzip berechnet werden; es muss lediglich das
negative Vorzeichen des Volumenstroms berücksichtigt werden.
abfließende Wassermenge kann
wiederum nach dem obigen Prinzip berechnet werden; es muss lediglich das
negative Vorzeichen des Volumenstroms berücksichtigt werden.![\int_{t_2}^{t_3} \dot{V}_2 \cdot \mathrm{d}t = \big( \dot{V}_2 \cdot t
\big) \Big | _{\mathrm{t_2}} ^{t_3} = \dot{V}_2 \cdot t_3 - \dot{V}_3
\cdot t_2 = \dot{V}_2 \cdot (t_3 - t_2) = \unit[-1,2]{\frac{l}{s}} \cdot
\unit[(50-45)]{s} = \unit[-6,0]{l}](../_images/math/c5201bb60b2924dfbaa127c53b315264bae55f0d.png)
Die resultierende Wassermenge ergibt sich aus der Addition beider Integrale:
![V_{\mathrm{ges}} = \int_{t_0}^{t_1} \dot{V}_1 \cdot \mathrm{d}t +
\int_{t_2}^{t_3} \dot{V}_2 \cdot \mathrm{d}t = \unit[(9,0-6,0)]{l} =
\unit[3,0]{l}](../_images/math/e3a229ada676afff5e3c4d31f3483df39cbc6bdc.png)
Unter den angegebenen Bedingungen werden zum Zeitpunkt
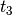 somit drei
Liter Wasser im Waschbecken sein.
somit drei
Liter Wasser im Waschbecken sein.
Das Integral
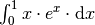 kann am
Einfachsten mittels einer partiellen Integration berechnet werden, indem man sich die gegebene Funktion in der
Gestalt
kann am
Einfachsten mittels einer partiellen Integration berechnet werden, indem man sich die gegebene Funktion in der
Gestalt 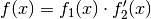 denkt; hierbei soll
denkt; hierbei soll 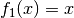 und
und 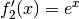 gesetzt werden.
gesetzt werden.Für eine partielle Integration gilt allgemein:
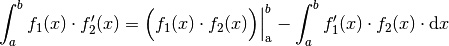
Zur Berechnung des Integrals muss somit die Ableitung der Funktion
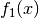 sowie die Stammfunktion der Funktion
sowie die Stammfunktion der Funktion 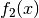 gefunden
werden:
gefunden
werden:
Somit ergibt sich:
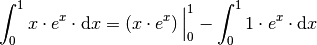
Das Integral
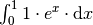 kann
unmittelbar als
kann
unmittelbar als 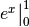 geschrieben werden, da die Stammfunktion
zu
geschrieben werden, da die Stammfunktion
zu 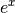 wiederum
wiederum 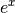 ist. Damit erhält man für die obige
Gleichung:
ist. Damit erhält man für die obige
Gleichung: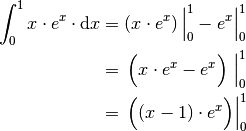
Die beiden Terme dürfen in der zweiten Zeile zusammen gezogen werden, da für beide die gleichen Integrationsgrenzen gelten. Zur Auswertung müssen diese nun noch eingesetzt werden. Damit erhält man:
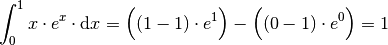
Das Integral ergibt wegen
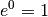 somit den Wert
somit den Wert 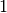 .
.
