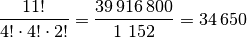Kombinatorik¶
In der Kombinatorik wird untersucht, wie viele unterschiedliche Möglichkeiten sich bei der Anordnung einer bestimmten Anzahl an Objekten ergeben, je nachdem, ob dabei die Reihenfolge der Objekte berücksichtigt wird und/oder die Objekte wiederholt auftreten können.
Permutationen¶
Eine Menge mit  Elementen soll unter Berücksichtigung der Reihenfolge
angeordnet werden, wobei jedes Element nur einmal vorkommen darf. Wie viele
verschiedene Anordnungen sind dabei möglich?
Elementen soll unter Berücksichtigung der Reihenfolge
angeordnet werden, wobei jedes Element nur einmal vorkommen darf. Wie viele
verschiedene Anordnungen sind dabei möglich?
Diese Grundfrage lässt sich beantworten, indem Schritt für Schritt geprüft wird,
wie viele Möglichkeiten sich bei der Besetzung jeder einzelnen Stelle ergeben.
Für die Besetzung der ersten Stelle gibt es  Möglichkeiten, da noch
kein Element vergeben wurde. Für die Besetzung der zweiten Stelle bleiben nur
noch
Möglichkeiten, da noch
kein Element vergeben wurde. Für die Besetzung der zweiten Stelle bleiben nur
noch 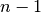 Möglichkeiten, da ein Element bereits an der ersten Stelle
vergeben wurde. Für die Besetzung der dritten Stelle bleiben entsprechend noch
Möglichkeiten, da ein Element bereits an der ersten Stelle
vergeben wurde. Für die Besetzung der dritten Stelle bleiben entsprechend noch
 Möglichkeiten, und so weiter. Für die letzte Stelle bleibt nur noch
ein Element übrig, somit gibt es auch nur eine Möglichkeit die Stelle zu
besetzen.
Möglichkeiten, und so weiter. Für die letzte Stelle bleibt nur noch
ein Element übrig, somit gibt es auch nur eine Möglichkeit die Stelle zu
besetzen.
Jede Besetzung einer einzelnen Stelle kann mit jeder Besetzung einer anderen
Stelle kombiniert werden. Damit entspricht die Anzahl an
 -Permutationen, d.h. an Anordnungen mit Berücksichtigung der
Reihenfolge und ohne Wiederholung der Elemente, dem Produkt aller Möglichkeiten
für die einzelnen Stellen:
-Permutationen, d.h. an Anordnungen mit Berücksichtigung der
Reihenfolge und ohne Wiederholung der Elemente, dem Produkt aller Möglichkeiten
für die einzelnen Stellen:
(1)¶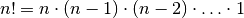
Dabei wird mit 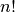 (gelesen:
(gelesen:  Fakultät) die Produktfolge von
Fakultät) die Produktfolge von 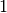 bis
bis  bezeichnet.
bezeichnet.
Beispiel:
Auf wie viele verschiedene Arten lassen sich ein roter, ein grüner, ein blauer, ein gelber und ein weißer Ball in einer Reihe hintereinander legen?
Da es sich insgesamt um fünf Bälle handelt und jeder Ball die erste Position in der Reihe einnehmen kann, gibt es für die Besetzung der ersten Stelle
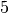 Möglichkeiten. Für jede mögliche Besetzung der ersten Stelle gibt
es
Möglichkeiten. Für jede mögliche Besetzung der ersten Stelle gibt
es 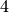 Möglichkeiten, die zweite Stelle zu besetzen, und für jede dieser
Anordnungen existieren wiederum
Möglichkeiten, die zweite Stelle zu besetzen, und für jede dieser
Anordnungen existieren wiederum 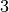 Möglichkeiten zur Besetzung der
dritten Stelle. Schließlich gibt es für jede dieser Anordnungen dreier Bälle
Möglichkeiten zur Besetzung der
dritten Stelle. Schließlich gibt es für jede dieser Anordnungen dreier Bälle
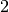 Möglichkeiten zur Besetzung der vierten Stelle. Die fünfte Stelle
ist automatisch festgelegt, da jeweils nur
Möglichkeiten zur Besetzung der vierten Stelle. Die fünfte Stelle
ist automatisch festgelegt, da jeweils nur 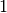 Besetzungsmöglichkeit
vorliegt. Insgesamt ergibt sich damit folgende Anzahl an Möglichkeiten:
Besetzungsmöglichkeit
vorliegt. Insgesamt ergibt sich damit folgende Anzahl an Möglichkeiten: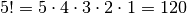
Es gibt somit
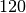 verschiedene Möglichkeiten, die fünf Bälle der Reihe
nach anzuordnen.
verschiedene Möglichkeiten, die fünf Bälle der Reihe
nach anzuordnen.
Permutationen mit nicht unterscheidbaren Objekten
Sind 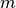 von den insgesamt
von den insgesamt  Objekten nicht unterscheidbar, so
können diese auf
Objekten nicht unterscheidbar, so
können diese auf 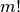 verschiedene Arten auf ihre Positionen verteilt
werden. Da alle diese Möglichkeiten nur eine einzige Anordnung liefern,
würden sie in der Permutations-Gleichung (1)
fälschlicherweise zu einem
verschiedene Arten auf ihre Positionen verteilt
werden. Da alle diese Möglichkeiten nur eine einzige Anordnung liefern,
würden sie in der Permutations-Gleichung (1)
fälschlicherweise zu einem 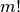 -fachen an Kombinationsmöglichkeiten
führen.
-fachen an Kombinationsmöglichkeiten
führen.
Um die Einschränkung an unterschiedlichen Anordnungen zu berücksichtigen, muss
Gleichung (1) durch 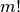 dividiert werden. Die
Anzahl an
dividiert werden. Die
Anzahl an  -Permutationen mit
-Permutationen mit 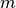 identischen Objekten ist somit
gleich
identischen Objekten ist somit
gleich 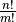 .
.
Sind allgemein jeweils 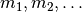 der insgesamt
der insgesamt
 Objekte identisch, so lässt sich die Anzahl an Permutationen
(unterschiedlichen Anordnungen) folgendermaßen berechnen:
Objekte identisch, so lässt sich die Anzahl an Permutationen
(unterschiedlichen Anordnungen) folgendermaßen berechnen:
(2)¶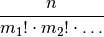
Beispiele:
Auf wie viele verschiedene Arten lassen sich die Ziffern
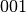 anordnen?
anordnen?In diesem Fall treten zwei gleichartige Objekte (die zwei Nullen) auf. Für die Anzahl der möglichen Permutationen gilt somit:
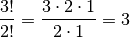
Es sind somit drei verschiedene Permutationen
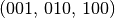 möglich.
möglich.Auf wie viele verschiedene Arten lassen sich die Buchstaben des Wortes „Mississippi“ anordnen?
Wären alle elf Buchstaben voneinander verschieden, so gäbe es
unterschiedliche Anordnungsmöglichkeiten. Von diesen Anordnungen sind allerdings
identisch, da es sich bei den vier Buchstaben „i“, den vier Buchstaben „s“ und den zwei Buchstaben „p“ um nicht unterscheidbare Objekte handelt, und die verschiedenen Anordnungsmöglichkeiten der gleichen Buchstaben jeweils zu nur einer einzigen zusammenfallen. Insgesamt ergibt sich somit folgende Anzahl an möglichen Anordnungen:
Es gibt also
verschiedene Möglichkeiten, die elf Buchstaben unter Berücksichtigung der Reihenfolge anzuordnen.
Variationen¶
Bei einer Variation wird aus einer Menge von  -Elementen eine Auswahl an
-Elementen eine Auswahl an
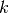 Elementen entnommen; dabei wird die Reihenfolge der entnommenen
Elemente berücksichtigt.
Elementen entnommen; dabei wird die Reihenfolge der entnommenen
Elemente berücksichtigt.
Variationen ohne Wiederholung
Wird aus einer Menge mit  Elementen eine Anzahl an
Elementen eine Anzahl an 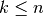 Elementen entnommen, wobei kein Element mehrfach vorkommen darf, so ergibt sich
(unter Berücksichtigung der Reihenfolge) eine bestimmte Anordnung der
Elementen entnommen, wobei kein Element mehrfach vorkommen darf, so ergibt sich
(unter Berücksichtigung der Reihenfolge) eine bestimmte Anordnung der 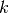 Elemente. Mathematisch wird eine solche Anordnung
Elemente. Mathematisch wird eine solche Anordnung 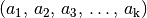 als „Tupel“ bezeichnet.[1]
als „Tupel“ bezeichnet.[1]
An der ersten Stelle des Tupels kann jedes der  Elemente auftreten.
Für die Besetzung der zweiten Stelle sind nur noch
Elemente auftreten.
Für die Besetzung der zweiten Stelle sind nur noch  Möglichkeiten
vorhanden, für die Besetzung der dritten Stelle
Möglichkeiten
vorhanden, für die Besetzung der dritten Stelle  Möglichkeiten.
Für die Besetzung
Möglichkeiten.
Für die Besetzung 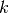 -ten Stelle gibt es schließlich
-ten Stelle gibt es schließlich 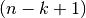 verschiedene Möglichkeiten. Die Anzahl an möglichen Tupeln ist
somit insgesamt gleich:
verschiedene Möglichkeiten. Die Anzahl an möglichen Tupeln ist
somit insgesamt gleich:
(3)¶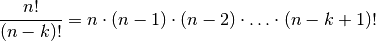
Da 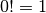 gilt, kann im Fall
gilt, kann im Fall 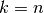 die obige Formel
(3) als
die obige Formel
(3) als 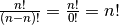 geschrieben werden. Dieser Fall entspricht somit einer
Permutation der
geschrieben werden. Dieser Fall entspricht somit einer
Permutation der  Elemente beziehungsweise der Gleichung
(1). Im Fall
Elemente beziehungsweise der Gleichung
(1). Im Fall 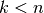 wird die Produktreihe vorzeitig
„abgeschnitten“.
wird die Produktreihe vorzeitig
„abgeschnitten“.
Variationen mit Wiederholung
Wird aus einer Menge mit  Elementen eine Anzahl an
Elementen eine Anzahl an 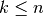 Elementen entnommen, wobei jedes Element mehrfach vorkommen darf, so spricht man
von einer Variation mit Wiederholung. Jedes Ergebnis ist wiederum ein Tupel
Elementen entnommen, wobei jedes Element mehrfach vorkommen darf, so spricht man
von einer Variation mit Wiederholung. Jedes Ergebnis ist wiederum ein Tupel
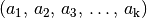 .
.
An jeder Stelle des Tupels kann, wenn eine Wiederholung der Elemente möglich
ist, jedes der  Elemente auftreten. Die Anzahl an möglichen Tupeln ist
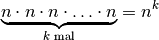
somit gleich:
Elemente auftreten. Die Anzahl an möglichen Tupeln ist
somit gleich:
(4)¶
Beispiel:
Aus einer Liste mit
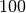 verschiedenen Zitaten wird jeden Tag nach
einem Zufallsprinzip ein Zitat ausgewählt, um als „Zitat des Tages“ auf einer
Homepage eingeblendet zu werden. Wie viele verschiedene Variationen der Zitate
können in
verschiedenen Zitaten wird jeden Tag nach
einem Zufallsprinzip ein Zitat ausgewählt, um als „Zitat des Tages“ auf einer
Homepage eingeblendet zu werden. Wie viele verschiedene Variationen der Zitate
können in 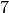 Tagen auftreten?
Tagen auftreten?An jedem der Tage sind
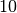 verschiedene Zitate möglich, denn es kann
auch an zwei oder mehreren aufeinander folgenden Tagen das gleiche Zitat
erscheinen. Innerhalb einer Woche gilt damit für die Anzahl an möglichen
Zitatefolgen:
verschiedene Zitate möglich, denn es kann
auch an zwei oder mehreren aufeinander folgenden Tagen das gleiche Zitat
erscheinen. Innerhalb einer Woche gilt damit für die Anzahl an möglichen
Zitatefolgen: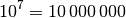
Innerhalb einer Woche können somit zehn Millionen verschiedene Anordnungen der Zitate auftreten.
Kombinationen¶
Bei einer Kombination wird aus einer Menge von  -Elementen eine Auswahl
an
-Elementen eine Auswahl
an 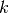 Elementen entnommen; dabei wird die Reihenfolge der entnommenen
Elemente nicht berücksichtigt.
Elementen entnommen; dabei wird die Reihenfolge der entnommenen
Elemente nicht berücksichtigt.
Kombinationen ohne Wiederholung
Um 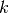 Elemente in einer bestimmten Reihenfolge aus einer Menge mit
Elemente in einer bestimmten Reihenfolge aus einer Menge mit
 Elementen auszuwählen, gibt es, wie im Abschnitt Variationen
ohne Wiederholung besprochen,
Elementen auszuwählen, gibt es, wie im Abschnitt Variationen
ohne Wiederholung besprochen,
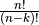 Möglichkeiten. Hierbei wurde allerdings jede
Reihenfolge der
Möglichkeiten. Hierbei wurde allerdings jede
Reihenfolge der 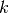 Elemente als eigene Möglichkeit angesehen. Soll die
Reihenfolge der entnommenen Elemente nicht berücksichtigt werden, so muss die
Gesamtzahl
Elemente als eigene Möglichkeit angesehen. Soll die
Reihenfolge der entnommenen Elemente nicht berücksichtigt werden, so muss die
Gesamtzahl 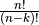 durch die Anzahl der möglichen Anordnungen der
durch die Anzahl der möglichen Anordnungen der
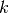 Elemente dividiert werden (also durch
Elemente dividiert werden (also durch 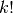 ).
).
Die sich ergebende Größe heißt Binomialkoeffizient und wird folgendermaßen dargestellt:
(5)¶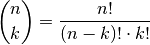
Die Werte der Binomialkoeffizienten lassen sich als so genanntes „Pascalsches
Dreieck“ anordnen. Da bei der Nummerierung der Zeilen und Spalten mit
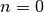 beziehungsweise
beziehungsweise 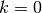 begonnen wird, befindet sich der
Koeffizient
begonnen wird, befindet sich der
Koeffizient 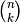 in der
in der 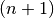 -ten Zeile an der
-ten Zeile an der
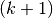 -ten Stelle.
-ten Stelle.
Jede Zahl ist die Summe der beiden darüber liegenden Zahlen. Die Werte Binomialkoeefizienten können somit rekursiv nach folgender Formel berechnet werden:
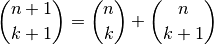
Beispiel:
Wie viele Möglichkeiten gibt es,
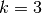 Kugeln aus einer Schale mit
Kugeln aus einer Schale mit
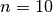 durchnummerierten Kugeln zu entnehmen, wenn die Reihenfolge keine
Rolle spielt?
durchnummerierten Kugeln zu entnehmen, wenn die Reihenfolge keine
Rolle spielt?Durch Einsetzen von
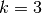 und
und 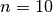 in Gleichung
(5) erhält man:
in Gleichung
(5) erhält man: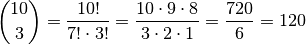
Es gibt somit
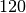 verschiedene Möglichkeiten, aus zehn nummerierten
Kugeln drei Stück auszuwählen.
verschiedene Möglichkeiten, aus zehn nummerierten
Kugeln drei Stück auszuwählen.
Kombinationen mit Wiederholung
Wird aus einer Menge mit  Elementen eine Anzahl an
Elementen eine Anzahl an 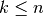 Elementen entnommen, wobei jedes Element mehrfach vorkommen darf und die
Reihenfolge der entnommenen Elemente nicht berücksichtigt wird, so spricht man
von einer Kombination mit Wiederholung.[2] Hierfür gibt es folgende Anzahl an
Möglichkeiten:
Elementen entnommen, wobei jedes Element mehrfach vorkommen darf und die
Reihenfolge der entnommenen Elemente nicht berücksichtigt wird, so spricht man
von einer Kombination mit Wiederholung.[2] Hierfür gibt es folgende Anzahl an
Möglichkeiten:
(6)¶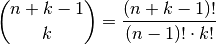
Formal ist diese Formel mit der Binomialkoeffizienten-Gleichung
(5) identisch, wenn man  durch
den Wert
durch
den Wert 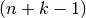 ersetzt.
ersetzt.
Beispiel:
Wie viele Möglichkeiten gibt es bei einem
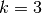 -fachen Werfen eines
Würfels mit
-fachen Werfen eines
Würfels mit 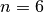 verschiedenen Seiten, wenn die Reihenfolge keine Rolle
spielt?
verschiedenen Seiten, wenn die Reihenfolge keine Rolle
spielt?Durch Einsetzen von
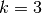 und
und 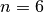 in Gleichung
(6) erhält man:
in Gleichung
(6) erhält man: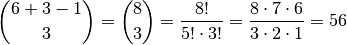
Es gibt bei dreimaligem Werfen des Würfels somit
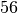 verschiedene
Kombinationen an erhaltenen Werten.
verschiedene
Kombinationen an erhaltenen Werten.
Anmerkungen:
| [1] | Auch geordnete Paare zweier Zahlen, beispielsweise die Koordinaten
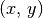 eines Punktes in einem zweidimensionalen
Koordinatensystem, können somit als Tupel bezeichnet werden. eines Punktes in einem zweidimensionalen
Koordinatensystem, können somit als Tupel bezeichnet werden. |
| [2] | Da jedes Element mehrfach vorkommen darf, ist bei Kombinationen mit
Wiederholung auch 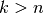 möglich. möglich. |