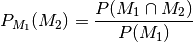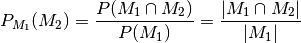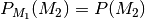Bedingte Wahrscheinlichkeit

Definition:

Bei einem Zufallsexperiment mit der Ergebnismenge werden zwei Ereignisse und mit betrachtet. Dann bezeichnet man folgenden Ausdruck als bedingte Wahrscheinlichkeit von unter der Bedingung :

Handelt es sich bei und um Laplace-Wahrscheinlichkeiten, so gilt:

Die obige Definition lässt sich auch, insbesondere bei der Nutzung von Baumdiagrammen, als Produktsatz formulieren. Es gilt für die Wahrscheinlichkeit, dass sowohl 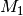als auch 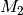eintreten:

Für bedingte Wahrscheinlichkeiten gelten zudem folgende Regeln:

• Multiplikationsregel: In einem Ergebnisbaum stellt jeder Knoten ein Elementarereignis dar. Die Wahrscheinlichkeit eines bestimmten Ereignisses entspricht dabei dem Produkt der Wahrscheinlichkeiten aller Elementarereignisse längs des zugehörigen Weges.
• Additionsregel: Besteht ein Ereignis in einem Ereignisbaum aus mehreren Wegen, so ist die zugehörige Wahrscheinlichkeit gleich der Summe der Wahrscheinlichkeiten für die einzelnen Wege.

Stochatisch unabhängige Ereignisse

Ein Ereignis 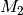ist von einem Ereignis 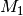unabhängig, wenn 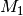auf die Wahrscheinlichkeit von 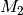keinen Einfluss hat.

Definition:

Ist die Ergebnismenge eines Zufallsexperiments und und zwei Ereignisse mit , so nennt man stochastisch unabhängig von , wenn gilt:

Andernfalls heißt stochastisch abhängig von .

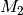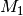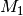Ist ein Ereignis stochastisch unabhängig vom Ereignis , so ist umgekehrt auch stochastisch unabhängig von 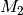, denn in diesem Fall gilt:

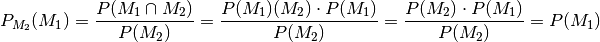
Als Sonderfall von stochastischer Unabhängigkeit gilt 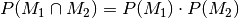stets auch dann, wenn die Wahrscheinlichkeit von mindestens einem der beiden Ereignisse gleich Null ist. Allgemein gilt für alle stochastisch unabhängigen Ereignisse:

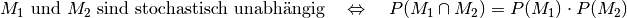
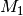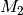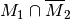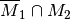Sind zwei Ereignisse und stochastisch unabhängig, so gilt dies auch für die Gegenereignisse. In diesem Fall sind somit auch die Ereignisse , sowie 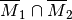stochastisch unabhängig.