Wahrscheinlichkeitsmaße¶
Die relative Häufigkeit¶
Um die relative Häufigkeit eines Ereignisses 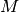 bei einem
Zufallsexperiment zu bestimmen, wird dieses
bei einem
Zufallsexperiment zu bestimmen, wird dieses  mal durchgeführt und
gezählt, wie oft das Ereignis
mal durchgeführt und
gezählt, wie oft das Ereignis 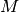 eintritt. Die relative Häufigkeit
eintritt. Die relative Häufigkeit
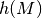 ist dabei folgendermaßen definiert:
ist dabei folgendermaßen definiert:
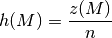
Die Größe 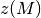 wird dabei „absolute“ Häufigkeit des Ereignisses
wird dabei „absolute“ Häufigkeit des Ereignisses
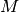 genannt und gibt an, wie häufig das Ereignis
genannt und gibt an, wie häufig das Ereignis 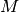 bei dem
Zufallsexperiment insgesamt eingetreten ist.
bei dem
Zufallsexperiment insgesamt eingetreten ist.
Bei großen Versuchszahlen gilt für die relative Häufigkeit das so genannte
Gesetz der großen Zahlen: Die relative Häufigkeit 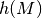 eines
Ereignisses
eines
Ereignisses 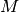 weicht bei einem genügend großen Wert von
weicht bei einem genügend großen Wert von  nur
wenig von einem bestimmten, für das Ereignis charakteristischen Wert ab.
nur
wenig von einem bestimmten, für das Ereignis charakteristischen Wert ab.
Besteht die Menge 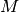 aus den Elementen
aus den Elementen  , so gilt für die relative Häufigkeit bei einer Reihe von
, so gilt für die relative Häufigkeit bei einer Reihe von  Versuchen:
Versuchen:
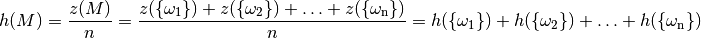
Die relative Häufigkeit von 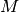 ist also gleich der Summe der relativen
Häufigkeiten aller Elementarereignisse, die in
ist also gleich der Summe der relativen
Häufigkeiten aller Elementarereignisse, die in 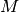 enthalten sind.
enthalten sind.
Allgemein gilt für die relative Häufigkeit stets 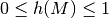 ,
wobei
,
wobei 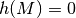 für ein unmögliches und
für ein unmögliches und 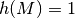 für ein
sicheres Ereignis gilt. Sind zudem zwei Ereignisse
für ein
sicheres Ereignis gilt. Sind zudem zwei Ereignisse 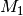 und
und 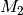 unvereinbar, d.h. gilt
unvereinbar, d.h. gilt 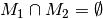 , so gilt
, so gilt 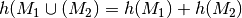 .
.
Die Wahrscheinlichkeit¶
Als Wahrscheinlichkeit bezeichnet man ein Maß für das Eintreten eines
Ereignisses 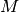 .
.
Prinzipiell kann nach dem empirischen Gesetz der großen Zahlen für die Wahrscheinlichkeit folgende Festsetzung genutzt werden:
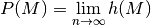
In der Praxis lassen sich jedoch stets nur eine begrenzte Zahl  an
Versuchen durchführen. Man definiert den Wahrscheinlichkeitsbegriff daher
über folgende Axiome:
an
Versuchen durchführen. Man definiert den Wahrscheinlichkeitsbegriff daher
über folgende Axiome:
Definition:
Eine Abbildung der Form
heißt Wahrscheinlichkeitsmaß, wenn folgende Eigenschaften („Axiome von Kolmogoroff“) erfüllt sind:
Nichtnegativität: Für alle
gilt:
Normiertheit: Ist
, so gilt:
Additivität: Für
gilt:
Die Additivität gilt auch für mehrere Ereignisse
, wenn diese paarweise unvereinbar sind, d.h. wenn
für
gilt.
Die Zahl 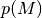 wird dabei als Wahrscheinlichkeit des Ereignisses
wird dabei als Wahrscheinlichkeit des Ereignisses
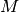 bezeichnet.
bezeichnet.
Zu einem Zufallsexperiment sind beliebig viele unterschiedliche
Wahrscheinlichkeitsmaße denkbar. Welches Maß dabei das „Richtige“ ist, hängt
von den physikalischen Gegebenheiten des Experiments ab. Bei einem „normalen“
Würfel erwartet man beispielsweise, dass die Wahrscheinlichkeit 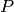 für
jede Augenzahl gleich
für
jede Augenzahl gleich 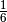 ist; hat der Würfel jedoch kleine
Unregelmäßigkeiten, so können diese zur Folge haben, dass nicht mehr alle
Elementarereignisse gleich wahrscheinlich sind.
ist; hat der Würfel jedoch kleine
Unregelmäßigkeiten, so können diese zur Folge haben, dass nicht mehr alle
Elementarereignisse gleich wahrscheinlich sind.
Zusätzlich zu den obigen Axiomen gelten als Folgerungen einige weitere Eigenschaften für Wahrscheinlichkeitsmaße:
- Ist
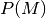 die Wahrscheinlichkeit eines Ereignisses
die Wahrscheinlichkeit eines Ereignisses 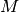 , so ist
, so ist
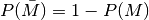 die Wahrscheinlichkeit des Gegenereignisses
die Wahrscheinlichkeit des Gegenereignisses
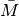 .[1]
.[1] - Ist
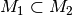 , so gilt
, so gilt 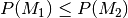 .
Diese Eigenschaft wird auch „Monotonieregel“ genannt.[2]
.
Diese Eigenschaft wird auch „Monotonieregel“ genannt.[2] - Es gilt stets:
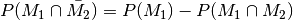 .
Diese Eigenschaft wird auch „Zerlegungsregel“ genannt.[3]
.
Diese Eigenschaft wird auch „Zerlegungsregel“ genannt.[3] - Es gilt stets:
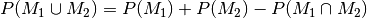 Diese Eigenschaft wird auch „Additionsregel“ genannt.[4]
Diese Eigenschaft wird auch „Additionsregel“ genannt.[4]
Wahrscheinlichkeit bei Laplace-Experimenten
Sind alle Elementarereignisse gleich wahrscheinlich, so bezeichnet man das Zufallsexperiment als „Laplace-Experiment“. Wahrscheinlichkeiten, die unter dieser Annahme berechnet werden, nennt man entsprechend „Laplace-Wahrscheinlichkeiten“.
Hat ein Laplace-Experiment  Elementarereignisse, d.h. ist
Elementarereignisse, d.h. ist
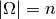 , so gilt
, so gilt 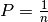 für jedes
Elementarereignis
für jedes
Elementarereignis 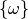 . Für ein Ereignis
. Für ein Ereignis 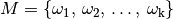 mit
mit  gilt
entsprechend:
gilt
entsprechend:
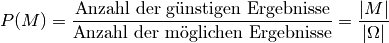
Um die Anzahl der günstigen und der möglichen Ergebnisse zu bestimmen, werden üblicherweise Methoden aus der Kombinatorik genutzt.
Anmerkungen:
| [1] | Dass diese Gleichung gilt, folgt aus 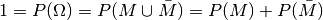 . . |
| [2] | Dass diese Gleichung gilt, lässt sich wegen
Wegen |
| [3] | Diese Eigenschaft ergibt sich aus 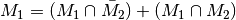 . Damit gilt ebenfalls . Damit gilt ebenfalls 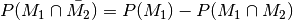 . . |
| [4] | Diese Eigenschaft gilt wegen 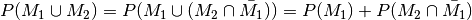 . Aufgrund der obigen
Beziehung gilt zudem . Aufgrund der obigen
Beziehung gilt zudem 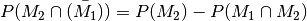 . Ein Einsetzen der zweiten Gleichung in die erste liefert die
Additionsregel. . Ein Einsetzen der zweiten Gleichung in die erste liefert die
Additionsregel. |

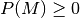
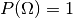
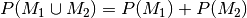
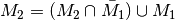 zeigen:
zeigen: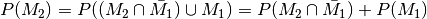
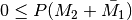 folgt
folgt