Trigonometrische Funktionen¶
Die trigonometrischen Funktionen, auch „Winkelfunktionen“ genannt, weisen jedem Winkel eine bestimmte Zahl zu, die das Längenverhältnis der entsprechenden Seiten in einem rechtwinkligen Dreieck angibt.
Die Winkelfunktionen am Einheitskreis¶
Die beiden Winkelfunktionen Sinus und Cosinus lassen sich nicht nur als
Längenverhältnisse in einem rechtwinkligen Dreieck, sondern auch als Streckenanteile interpretieren.
Zeichnet man in ein Koordinatensystem einen Kreis mit Radius eins um den
Koordinatenursprung 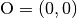 und verbindet den Koordinatenursprung
mit einem auf dem Kreis entlang wandernden Punkt
und verbindet den Koordinatenursprung
mit einem auf dem Kreis entlang wandernden Punkt  , so stellen
Cosinus und Sinus die senkrechten Projektionen der Verbindungslinie auf die
, so stellen
Cosinus und Sinus die senkrechten Projektionen der Verbindungslinie auf die
 - bzw.
- bzw.  -Achse dar. Der Tangens entspricht der Steigung, welche
die Verbindungslinie
-Achse dar. Der Tangens entspricht der Steigung, welche
die Verbindungslinie 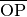 bei einem Winkel
bei einem Winkel 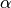 hat.
hat.

Sinus und Cosinus am Einheitskreis. Die Verbindungslinie
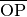 besitzt die Länge eins, so dass
besitzt die Länge eins, so dass
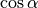 und
und 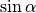 den Längen des
den Längen des  -
bzw.
-
bzw.  -Anteils von
-Anteils von 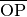 entsprechen.
entsprechen.
Der entscheidende Vorteil dieser Darstellung liegt darin, dass der Winkel
hierbei beliebig große Werte annehmen kann: Gilt für den Winkel 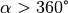 , so wiederholen sich auch die entsprechenden Werte von
, so wiederholen sich auch die entsprechenden Werte von
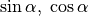 und
und 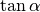 mit einer Periode
von
mit einer Periode
von 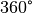 von neuem.[1]
von neuem.[1]
Damit sich die Winkelfunktionen in einem üblichen Koordinatensystem darstellen
lassen, wird der Winkel als Argument meist nicht im Gradmaß, sondern im
Bogenmaß angegeben. Damit kann, da sich die
trigonometrischen Funktionen für beliebig große Winkelwerte gelten, kann
beispielsweise auch 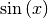 anstelle von
anstelle von 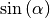 für
jedes
für
jedes 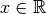 geschrieben werden.
Die Vorzeichen der Winkelfunktionen wiederum richten sich danach, in welchem
Quadranten des Koordinatensystems sich der „Kreisvektor“
geschrieben werden.
Die Vorzeichen der Winkelfunktionen wiederum richten sich danach, in welchem
Quadranten des Koordinatensystems sich der „Kreisvektor“ 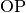 gerade
befindet.
gerade
befindet.
Anhand des Einheitskreises lässt sich auch der so genannte „trigonometrische
Pythagoras“ ableiten; Mit der Hypotenusenlänge 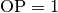 und den
Kathetenlängen
und den
Kathetenlängen 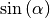 und
und 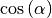 lautet der
Satz des Pythagoras hierbei:
lautet der
Satz des Pythagoras hierbei:
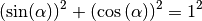
Gewöhnlich wird 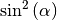 anstelle von
anstelle von
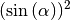 und
und 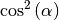 anstelle von
anstelle von
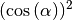 geschrieben. Für beliebige Winkelwerte
geschrieben. Für beliebige Winkelwerte 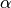 bzw.
bzw.  ergibt sich damit die folgende wichtige Beziehung:
ergibt sich damit die folgende wichtige Beziehung:
(1)¶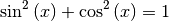
Eigenschaften und Funktionsgraphen der Winkelfunktionen
Für einige besondere Winkel 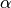 lassen sich die Werte der
Winkelfunktionen als (verhältnismäßig) einfache Bruch- bzw. Wurzelzahlen
angeben – für die übrigen Winkelmaße ergeben
lassen sich die Werte der
Winkelfunktionen als (verhältnismäßig) einfache Bruch- bzw. Wurzelzahlen
angeben – für die übrigen Winkelmaße ergeben 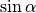 und
und
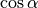 Werte mit unendlich vielen Nachkommastellen, die sich
periodisch stets zwischen
Werte mit unendlich vielen Nachkommastellen, die sich
periodisch stets zwischen 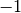 und
und 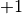 bewegen. Die Werte von
bewegen. Die Werte von
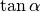 als dem Verhältnis von
als dem Verhältnis von 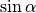 zu
zu
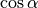 reichen von
reichen von 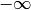 bis
bis 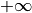 und sind nicht definiert, wenn
und sind nicht definiert, wenn 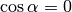 gilt.
gilt.
 |
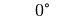 |
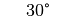 |
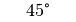 |
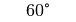 |
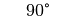 |
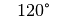 |
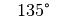 |
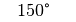 |
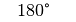 |
 |
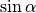 |
 |
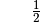 |
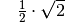 |
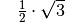 |
 |
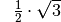 |
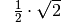 |
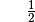 |
 |
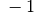 |
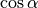 |
 |
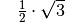 |
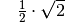 |
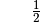 |
 |
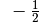 |
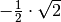 |
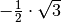 |
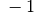 |
 |
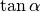 |
 |
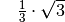 |
 |
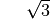 |
 |
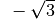 |
 |
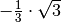 |
 |
 |
Die Werte der Winkelfunktionen 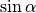 und
und 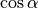 lassen sich auch als (wellenartige) Funktionsgraphen darstellen.
lassen sich auch als (wellenartige) Funktionsgraphen darstellen.
Die beiden Funktionen 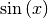 und
und 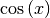 nehmen regelmäßig
wiederkehrend die gleichen Werte aus dem Wertebereich
nehmen regelmäßig
wiederkehrend die gleichen Werte aus dem Wertebereich ![\mathbb{W} =
[-1;1]](../../_images/math/4854bbc7d39efe498da9f3ac86d684996dcacb66.png) an. Sie werden daher als „periodisch“ bezeichnet, mit einer
Periodenlänge von
an. Sie werden daher als „periodisch“ bezeichnet, mit einer
Periodenlänge von 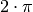 . Es gilt damit für jede natürliche Zahl
. Es gilt damit für jede natürliche Zahl
 :
:
(2)¶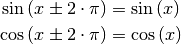
Führt man die Funktionsgraphen der Sinus- und Cosinusfunktion für negative
 -Werte fort, so kann man erkennen, dass es sich bei der Sinusfunktion
um eine ungerade (punktsymmetrische) Funktion und bei der Cosinusfunktion um
eine gerade (achsensymmetrische) Funktion handelt. Es gilt also:
-Werte fort, so kann man erkennen, dass es sich bei der Sinusfunktion
um eine ungerade (punktsymmetrische) Funktion und bei der Cosinusfunktion um
eine gerade (achsensymmetrische) Funktion handelt. Es gilt also:
(3)¶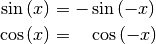
Zudem kann man den Funktionsgraphen der Cosinus-Funktion erhalten, indem man den
Funktionsgraphen der Sinus-Funktion um 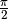 nach links (in
negative
nach links (in
negative  -Richtung) verschiebt; entsprechend ergibt sich die
Sinus-Funktion aus einer Verschiebung der Cosinusfunktion um
-Richtung) verschiebt; entsprechend ergibt sich die
Sinus-Funktion aus einer Verschiebung der Cosinusfunktion um
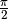 nach rechts. Es gilt somit unter Berücksichtigung der
Symmetrie der Cosinus-Funktion:
nach rechts. Es gilt somit unter Berücksichtigung der
Symmetrie der Cosinus-Funktion:
(4)¶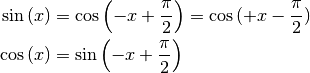
Da die Funktionswerte der Sinus- und Cosinusfunktion periodisch sind, sind auch
ihre Nullstellen periodisch. Sie lassen sich mit einer beliebigen natürlichen
Zahl  in folgender Form angeben:
in folgender Form angeben:
(5)¶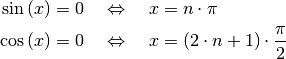
Die Tangensfunktion
Für die Tangens-Funktion 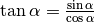 ergeben sich Vorzeichenwechsel an den Definitionslücken (den Stellen, an
denen
ergeben sich Vorzeichenwechsel an den Definitionslücken (den Stellen, an
denen 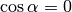 gilt). Je nachdem, von welcher Seite aus man
sich diesen „Polstellen“ nähert, nehmen die Funktionswerte des Tangens –
entsprechend der Vorzeichen von
gilt). Je nachdem, von welcher Seite aus man
sich diesen „Polstellen“ nähert, nehmen die Funktionswerte des Tangens –
entsprechend der Vorzeichen von 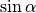 und
und 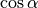 –
unendlich große negative bzw. positive Werte an.
–
unendlich große negative bzw. positive Werte an.
Die Nullstellen 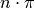 der Tangensfunktion sind mit denen der
Sinusfunktion identisch, die Polstellen entsprechen den Nullstellen
der Tangensfunktion sind mit denen der
Sinusfunktion identisch, die Polstellen entsprechen den Nullstellen  der Cosinusfunktion.
der Cosinusfunktion.
Additionstheoreme¶
Bisweilen treten in mathematischen und technischen Aufgaben Sinus- und Cosinusfunktionen auf, deren Argument eine Summe zweier Winkel ist. Oft ist es dabei hilfreich, diese als Verknüpfung mehrerer Sinus- bzw. Cosinusfunktionen mit nur einem Winkel als Argument angeben zu können. Die folgenden Rechenregeln, die eine derartige Umrechnung ermöglichen, werden üblicherweise als „Additionstheoreme“ bezeichnet.
Für beliebige Winkelwerte  und
und 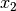 gilt:
gilt:
(6)¶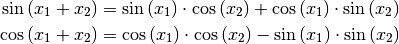
Ist  , so gilt wegen Gleichung (3):
, so gilt wegen Gleichung (3):
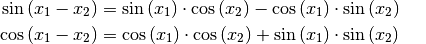
Ist 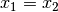 , so gelten folgende Rechenregeln für „doppelte“
Winkelwerte:
, so gelten folgende Rechenregeln für „doppelte“
Winkelwerte:
(7)¶![\sin{(2 \cdot x)} &= 2 \cdot \sin{(x)} \cdot \cos{(x)}\\[4pt]
\cos{(2 \cdot x)} &= \cos^2{(x)} -
\sin ^2{(x)} \\ &= 2 \cdot \cos^2{(x)} - 1 = 1 - 2 \cdot \sin ^2{(x)} {\color{white}\;\, 1}](../../_images/math/4dd2b09dd8f0ffb067b31d4803b13869c6e7b607.png)
Umgekehrt lassen sich Sinus und Cosinus auch umformen, indem man in den obigen
Gleichungen  durch
durch 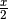 ersetzt. Es gilt dabei:
ersetzt. Es gilt dabei:
(8)¶![{\color{white}1 \;\;}\sin{(x)} &= 2 \cdot \sin{\left(\frac{x}{2}\right)} \cdot
\cos{\left(\frac{x}{2}\right)} \\[6pt]
\cos{(x)} &= \cos^2{\left(\frac{x}{2}\right)} - \sin
^2{\left(\frac{x}{2}\right)} \\[2pt]
&= 2 \cdot \cos^2{\left(\frac{x}{2}\right)} - 1 = 1 -2 \cdot \sin ^2{\left(\frac{x}{2}\right)}](../../_images/math/c54eaa895ffe7264bc393731b4d7bd0be61debb0.png)
Zudem gibt es (eher zum Nachschlagen) auch zwei Formeln, mit denen Summen oder Differenzen von gleichartigen Winkelfunktionen in Produkte verwandelt werden können, was insbesondere bei der Vereinfachung von Brüchen hilfreich sein kann:
(9)¶![\sin{(x_1)} + \sin{(x_2)} = 2 \cdot \sin{\left(
\frac{x_1+x_2}{2}\right)} \cdot \cos{\left(\frac{x_1-x_2}{2} \right)}{\color{white}\qquad\quad 1} \\[6pt]
\sin{(x_1)} - \sin{(x_2)} = 2 \cdot \cos{\left(
\frac{x_1+x_2}{2}\right)} \cdot \sin{\left(\frac{x_1-x_2}{2} \right)}{\color{white}\qquad\quad 1} \\](../../_images/math/c343f9ef252b97d2986c7349fbe379cba36d95d9.png)
Schließlich gibt es noch zwei Additionsregeln für die Summe bzw. die Differenz von Winkelargumenten bei Tangensfunktionen:
(10)¶![\tan{(x_1 + x_2)} &= \frac{\tan{(x_1)} + \tan{(x_2)}}{1 - \tan{(x_1)} \cdot \tan{(x_2)}}{\color{white}\qquad\qquad\qquad 1} \\[6pt]
\tan{(x_1 - x_2)} &= \frac{\tan{(x_1)} - \tan{(x_2)}}{1 + \tan{(x_1)} \cdot \tan{(x_2)}} \\](../../_images/math/deb702887228ada74ac60e52ed62efaeb6069c25.png)
Die Arcus-Funktionen¶
Die Arcus-Funktionen 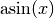 ,
, 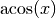 und
und
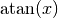 geben zu einem gegebenen Wert
geben zu einem gegebenen Wert  den zugehörigen
Winkel
den zugehörigen
Winkel 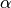 an; sie sind damit die Umkehrfunktionen der
trigonometrischen Funktionen
an; sie sind damit die Umkehrfunktionen der
trigonometrischen Funktionen 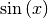 ,
, 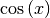 und
und
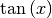 . Beispielsweise ist
. Beispielsweise ist 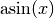 der Winkel im
Einheitskreis, dessen Sinus gleich
der Winkel im
Einheitskreis, dessen Sinus gleich  ist.
ist.
Da die Sinus-, Cosinus- und Tangensfunktionen aufgrund ihrer Periodizität nicht bijektiv sind, muss ihr Definitionsbereich bei der Bildung der jeweiligen Umkehrfunktion eingeschränkt werden. Die Arcus-Funktionen werden dabei üblicherweise mit folgenden Definitionsbereichen festgelegt:
- Die Umkehrfunktion zu
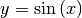 mit
mit ![x \in [-
\frac{\pi}{2};\frac{\pi}{2}]](../../_images/math/da97aa6690f7654b249c72c57e50f93398dc6ed8.png) ist die Funktion
ist die Funktion 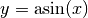 mit
mit
![x \in [1;1]](../../_images/math/b59a8d61b7c5e60402dbdacb390e5ea8de7940a7.png) .
.
- Die Umkehrfunktion zu
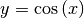 mit
mit ![x \in
[\phantom{-}\!0;\pi]](../../_images/math/5e4b83e3c12c587fc6a8688504f9620bd4b8427f.png) ist die Funktion
ist die Funktion 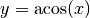 mit
mit ![x
\in [1;1]](../../_images/math/f440f7e49bbbf240d2bf933dd1e6f9e49a8589e0.png) .
.
- Die Umkehrfunktion zu
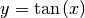 mit
mit ![x \in
[-\frac{\pi}{2};\frac{\pi}{2}]](../../_images/math/66e588eed64678dc7c87cbb50efd8c59a5a9779e.png) ist die Funktion
ist die Funktion 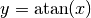 mit
mit
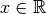 .
.
Die Wertebereiche der Arcus-Funktionen stimmen dabei mit den obigen Definitionsbereichen der ursprünglichen Winkelfunktionen überein.
Anmerkungen:
| [1] | Unter einer periodischen Funktion versteht man allgemein eine Funktion,
für die 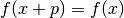 gilt; dabei wird gilt; dabei wird 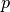 als Periode der
Funktion bezeichnet. als Periode der
Funktion bezeichnet. |



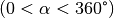 .
.
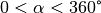 .
.

