Eigenschaften von Funktionen¶
Funktionen lassen sich anhand verschiedener Eigenschaften unterteilen. Wichtige Eigenschaften, die dabei von Bedeutung sind, werden im folgenden Abschnitt kurz zusammengefasst.[1]
Definitions- und Wertemenge¶
Die Menge an möglichen Werten, welche die Ausgangsgröße („Variable“)  annehmen kann, nennt man Definitionsmenge
annehmen kann, nennt man Definitionsmenge 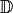 . Entsprechend
bezeichnet man die Menge an Werten, welche die Funktion
. Entsprechend
bezeichnet man die Menge an Werten, welche die Funktion 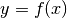 als
Ergebnisse liefert, als Wertemenge
als
Ergebnisse liefert, als Wertemenge 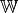 .
.
Bisweilen müssen einzelne Werte oder Intervalle aus der Definitionsmenge ausgeschlossen werden, um ein stets eindeutiges Verhalten der Funktion zu gewährleisten.
Beispiele:
- Bei der gebrochen-rationalen Funktion
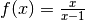 muss der Wert
muss der Wert 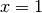 aus der Definitionsmenge ausgeschlossen werden, da
hierbei ansonsten durch Null dividiert würde.
aus der Definitionsmenge ausgeschlossen werden, da
hierbei ansonsten durch Null dividiert würde. - Bei der Wurzelfunktion
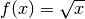 müssen alle Werte von
müssen alle Werte von
![]-\infty ;\; 0[](../_images/math/37f44905662e5c8dbc90d961fd6707bd8e92fcb6.png) ausgeschlossen werden, da die Wurzel nur für
positive
ausgeschlossen werden, da die Wurzel nur für
positive  -Werte definiert ist.
-Werte definiert ist.
Einzelne aus der Definitionsmenge ausgeschlossenen Werte nennt man Definitionslücken. Müssen hingegen Intervalle aus der Definitionsmenge ausgeschlossen werden, so bezeichnet man die verbleibende Definitionsmenge häufig als Definitionsbereich und gibt sie ebenfalls als Vereinigungsmenge von Intervallen an.
Im Folgenden werden ausschließlich „reellwertige“ Funktionen untersucht, das
heißt Vorschriften, die den reellen Werten einer (unabhängigen) Variablen
 ebenfalls reelle Werte der (von
ebenfalls reelle Werte der (von  abhängigen) Variablen
abhängigen) Variablen
 zuweisen. Hierbei gilt, sofern keine weiteren Einschränkungen zu
beachten sind, somit
zuweisen. Hierbei gilt, sofern keine weiteren Einschränkungen zu
beachten sind, somit 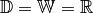 .[2]
.[2]
Darstellungen von Funktionen¶
Funktionen lassen sich im Allgemeinen auf drei verschiedene Arten darstellen:
- als Wertetabelle,
- als Graph in einem Koordinatensystem, und
- in Form einer Funktionsgleichung.
Wertetabellen sind dann sinnvoll, wenn einzelne Wertepaare 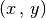 vorliegen, was insbesondere bei empirisch ermittelten (Mess-)Daten häufig der
Fall ist. Bei einer großen Anzahl von Wertepaaren können tabellarische
Darstellungen jedoch – ohne die Verwendung von Computern – schnell
unübersichtlich werden. Ein zweiter Nachteil liegt darin, dass fehlende
Funktionswerte zwischen zwei Wertepaaren nur durch Mittelwertbildung
(„Interpolation“) abgeschätzt werden können.
vorliegen, was insbesondere bei empirisch ermittelten (Mess-)Daten häufig der
Fall ist. Bei einer großen Anzahl von Wertepaaren können tabellarische
Darstellungen jedoch – ohne die Verwendung von Computern – schnell
unübersichtlich werden. Ein zweiter Nachteil liegt darin, dass fehlende
Funktionswerte zwischen zwei Wertepaaren nur durch Mittelwertbildung
(„Interpolation“) abgeschätzt werden können.
Bei graphischen Darstellungen werden die einzelnen Wertepaare 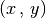 in eindeutiger Weise auf Punkte eines Koordinatensystems abgebildet.[3]
Sind die Abstände zwischen den Wertepaaren nur sehr gering, so kann der
funktionale Zusammenhang graphisch durch eine Kurve veranschaulicht werden. Dies
ermöglicht oftmals ein schnelles Ablesen der Funktionswerte (zumindest
näherungsweise). Beispielsweise kann auf diese Weise an Oszilloskopen oder
Kardiogrammen der zeitliche Verlauf eines elektrischen Spannungssignals direkt
beobachtet werden.[4]
in eindeutiger Weise auf Punkte eines Koordinatensystems abgebildet.[3]
Sind die Abstände zwischen den Wertepaaren nur sehr gering, so kann der
funktionale Zusammenhang graphisch durch eine Kurve veranschaulicht werden. Dies
ermöglicht oftmals ein schnelles Ablesen der Funktionswerte (zumindest
näherungsweise). Beispielsweise kann auf diese Weise an Oszilloskopen oder
Kardiogrammen der zeitliche Verlauf eines elektrischen Spannungssignals direkt
beobachtet werden.[4]
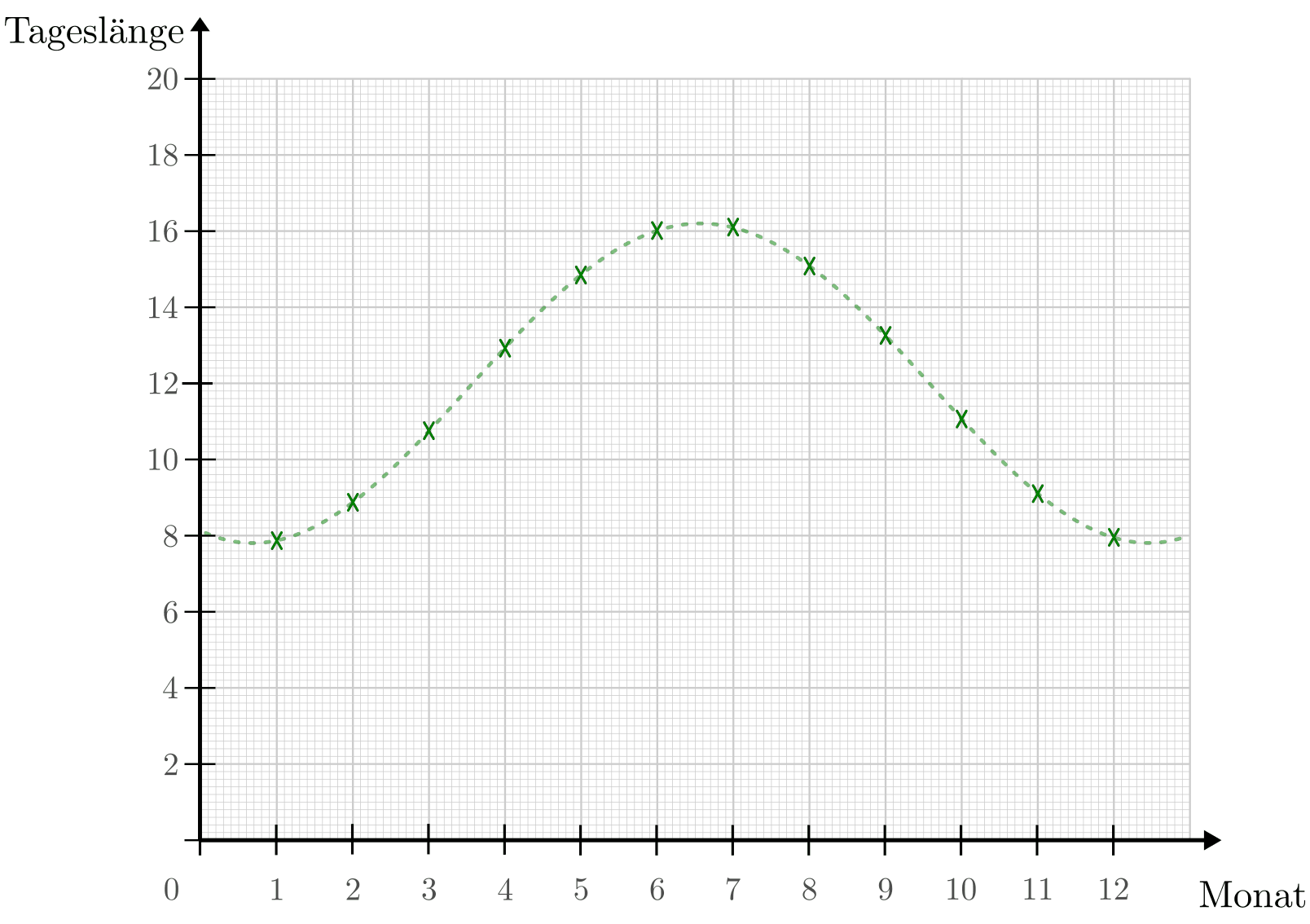
Darstellung von Wertepaaren mittels eines Diagramms (Beispiel: Tageslänge im Jahresverlauf am 50. Breitengrad).
Wie das Bild einer Funktion bei einer graphischen Darstellung konkret aussieht,
hängt auch von der Wahl des Koordinatensystems, insbesondere von der Skalierung
der Achsen ab. Weisen beispielsweise die  - und die
- und die  -Achse
unterschiedliche Skalierungen auf, so erscheint das Funktionsbild verzerrt.
-Achse
unterschiedliche Skalierungen auf, so erscheint das Funktionsbild verzerrt.
Zur rechnerischen Untersuchung einer Funktion wird die „analytische“ Form, also eine Darstellung als Funktionsgleichung bevorzugt. Eine Funktionsgleichung kann wiederum bei Bedarf jederzeit in eine Wertetabelle oder eine graphische Form gebracht werden. Man unterscheidet zwischen zwei Arten von Funktionsgleichungen:
Bei der expliziten Form ist die Funktionsgleichung nach der (abhängigen) Variablen
 aufgelöst.
aufgelöst.Beispiel:

Bei einer impliziten Form treten die unabhängige Variable
 und die
abhängige Variable
und die
abhängige Variable  auf der gleichen Seite der Gleichung auf; die
Gleichung hat damit die Form
auf der gleichen Seite der Gleichung auf; die
Gleichung hat damit die Form 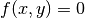 .
.Beispiel:
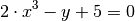
Nicht jede Funktion kann in einer nach  aufgelösten Form dargestellt
werden, beispielsweise
aufgelösten Form dargestellt
werden, beispielsweise 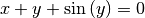 . Sofern möglich, wird im
Allgemeinen die explizite Darstellungsform
. Sofern möglich, wird im
Allgemeinen die explizite Darstellungsform 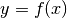 bevorzugt.[5]
bevorzugt.[5]
Surjektivität, Injektivität und Bijektivität¶
Die Unterscheidung von surjektiven, injektiven und bijektiven Funktionen ermöglicht eine wichtige Einteilung von Funktionen.
Eine Funktion heißt surjektiv, wenn jedes Element ihrer Wertemenge
 mindestens einmal als Funktionswert auftritt, also jedes
Element der Wertemenge mindestens einem Element der Definitionsmenge
zugeordnet ist.
mindestens einmal als Funktionswert auftritt, also jedes
Element der Wertemenge mindestens einem Element der Definitionsmenge
zugeordnet ist.Am Diagramm einer Funktion lässt sich diese Eigenschaft daran erkennen, dass jede beliebige, zur
 -Achse parallele Gerade den Funktionsgraph im
gesamten Wertebereich mindestens einmal schneidet.
-Achse parallele Gerade den Funktionsgraph im
gesamten Wertebereich mindestens einmal schneidet.Beispiel:
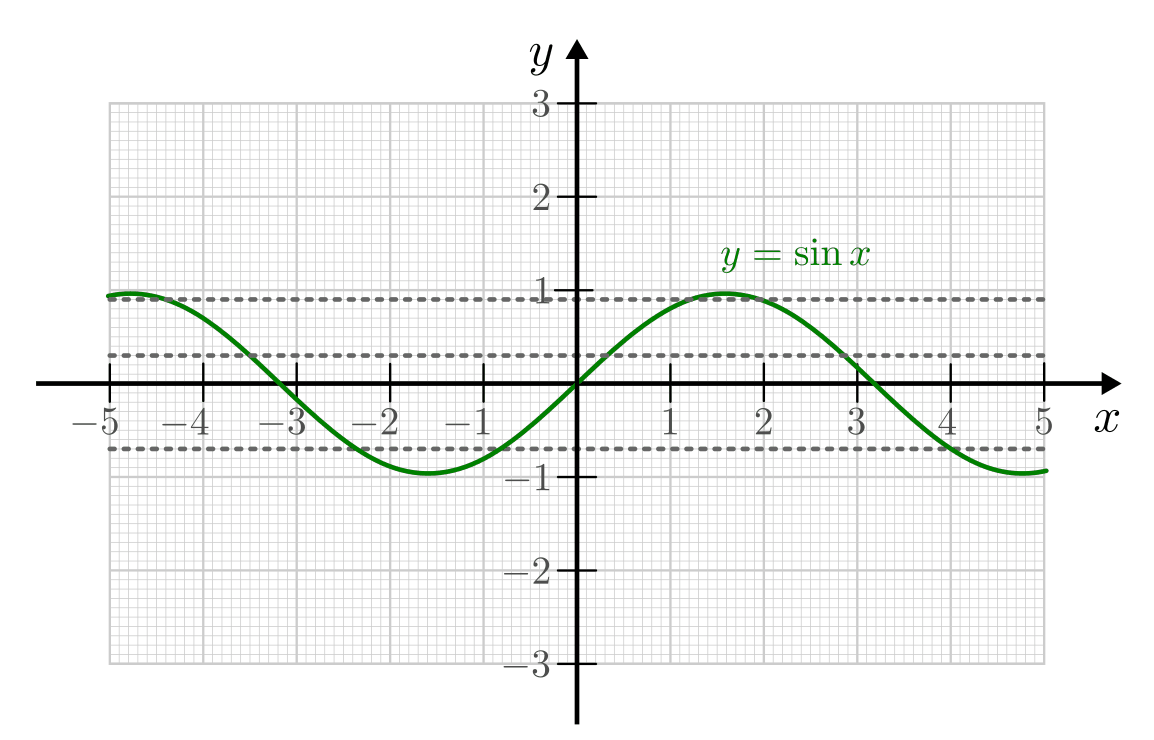
Die Sinus-Funktion
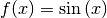 mit der Definitionsmenge
mit der Definitionsmenge
 und der Wertemenge
und der Wertemenge ![\mathbb{W} = [-1 ;\;
+1]](../_images/math/2700b9a66559985fbd3f8c40245305ab8befef31.png) ist surjektiv. Der Funktionsgraph wird von jeder zur
ist surjektiv. Der Funktionsgraph wird von jeder zur  -Achse
parallelen Geraden zwischen
-Achse
parallelen Geraden zwischen 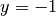 und
und  mindestens einmal
geschnitten.
mindestens einmal
geschnitten.
Eine Funktion heißt injektiv, wenn jedes Element ihrer Wertemenge
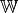 höchstens einmal als Funktionswert auftritt, also jedes
Element der Wertemenge maximal einem Element der Definitionsmenge zugeordnet
ist.
höchstens einmal als Funktionswert auftritt, also jedes
Element der Wertemenge maximal einem Element der Definitionsmenge zugeordnet
ist.Am Diagramm einer Funktion lässt sich diese Eigenschaft daran erkennen, dass jede beliebige, zur
 -Achse parallele Gerade den Funktionsgraph im
gesamten Wertebereich höchstens einmal schneidet.
-Achse parallele Gerade den Funktionsgraph im
gesamten Wertebereich höchstens einmal schneidet.Beispiel:
Die Funktion
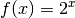 mit der Definitionsmenge
mit der Definitionsmenge 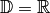 und der Wertemenge
und der Wertemenge 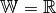 ist injektiv.
Der Funktionsgraph wird von jeder zur
ist injektiv.
Der Funktionsgraph wird von jeder zur  -Achse parallelen Geraden im
positiven Wertebereich
-Achse parallelen Geraden im
positiven Wertebereich 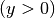 genau einmal, im negativen Wertebereich
genau einmal, im negativen Wertebereich
 überhaupt nicht geschnitten.
überhaupt nicht geschnitten.
Eine Funktion heißt bijektiv, wenn jedes Element ihrer Wertemenge
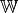 genau einmal als Funktionswert auftritt, also jedes
Element der Wertemenge genau einem Element der Definitionsmenge zugeordnet
ist.[6]
genau einmal als Funktionswert auftritt, also jedes
Element der Wertemenge genau einem Element der Definitionsmenge zugeordnet
ist.[6]Am Diagramm einer Funktion lässt sich diese Eigenschaft daran erkennen, dass jede beliebige, zur
 -Achse parallele Gerade den Funktionsgraph im
gesamten Wertebereich genau einmal schneidet.
-Achse parallele Gerade den Funktionsgraph im
gesamten Wertebereich genau einmal schneidet.Beispiel:
Die Funktion
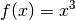 mit der Definitionsmenge
mit der Definitionsmenge 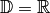 und der Wertemenge
und der Wertemenge 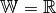 ist bijektiv;
der Funktionsgraph wird von jeder zur
ist bijektiv;
der Funktionsgraph wird von jeder zur  -Achse parallelen Geraden im
gesamten Wertebereich genau einmal geschnitten.
-Achse parallelen Geraden im
gesamten Wertebereich genau einmal geschnitten.
Jede surjektive oder injektive Funktion kann durch eine geeignete Einschränkung der Definitions- beziehungsweise Wertemenge zu einer entsprechenden bijektiven Funktion gemacht werden.[7]
Umkehrbarkeit einer Funktion¶
Eine Funktion ist eine mathematische Beschreibung dafür, welche „Ursache“
 innerhalb eines Prozesses eine bestimmte Wirkung
innerhalb eines Prozesses eine bestimmte Wirkung  hervorruft.
Ein derartiger Zusammenhang ist nur dann sinnvoll, wenn die Zuweisung eines
beliebigen Wertes der Ausgangsgröße
hervorruft.
Ein derartiger Zusammenhang ist nur dann sinnvoll, wenn die Zuweisung eines
beliebigen Wertes der Ausgangsgröße  zu einem Ergebniswert
zu einem Ergebniswert 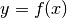 stets eindeutig ist, ein
stets eindeutig ist, ein  -Wert also nicht zwei verschiedene
-Wert also nicht zwei verschiedene
 -Werte als Ergebnis liefern kann.
-Werte als Ergebnis liefern kann.
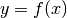
Umgekehrt ist es jedoch möglich, dass verschiedene  -Werte den gleichen
-Werte den gleichen
 -Wert als Ergebnis liefern.
-Wert als Ergebnis liefern.
Beispiele:
- Unterschiedliche Körper können eine gleich große Masse besitzen. Ein einzelner Körper hingegen besitzt stets nur einen einzigen, eindeutigen Wert für die Größe seiner Masse.
- In einem Obstladen kostet eine bestimmte Sorte Äpfel (zu einem bestimmten Zeitpunkt) einen eindeutigen Preis je Menge. Unabhängig davon, wie viele Äpfel ein Kunde tatsächlich kauft, ist der zu zahlende Gesamtbetrag dadurch eindeutig festgelegt. Der gleiche Preis je Menge kann gleichzeitig allerdings auch für eine andere Obstsorte gelten.
Im Allgemeinen sind Funktionen somit nicht „umkehrbar“, es lässt sich also nicht
für jede Funktion eine Zuordnung finden, die jedem beliebigen  -Wert auf
eindeutige Weise einen
-Wert auf
eindeutige Weise einen  -Wert zuweist. Eine Funktion besitzt diese
Eigenschaft genau dann, wenn sie bijektiv ist. Ist eine
Funktion nicht bijektiv, so muss sie zuerst durch Einschränkung ihrer
Definitions- beziehungsweise Wertemenge zu einer bijektiven Funktion gemacht werden.
-Wert zuweist. Eine Funktion besitzt diese
Eigenschaft genau dann, wenn sie bijektiv ist. Ist eine
Funktion nicht bijektiv, so muss sie zuerst durch Einschränkung ihrer
Definitions- beziehungsweise Wertemenge zu einer bijektiven Funktion gemacht werden.
Bestimmung der Umkehrfunktion
Die Umkehrfunktion 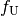 einer Funktion
einer Funktion 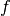 findet man,
indem man die ursprüngliche Funktionsgleichung
findet man,
indem man die ursprüngliche Funktionsgleichung 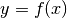 nach
nach  auflöst und anschließend die Variablen
auflöst und anschließend die Variablen  und
und  vertauscht.
vertauscht.
Beispiel:
Die Umkehrfunktion
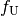 der Funktion
der Funktion 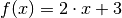 lässt sich berechnen, indem zunächst die Funktionsgleichung nach
lässt sich berechnen, indem zunächst die Funktionsgleichung nach  aufgelöst wird:
aufgelöst wird: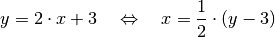
Multipliziert man in der rechten Gleichung die Klammer aus und vertauscht die Bezeichnungen der Variablen
 und
und  , so folgt für die
Umkehrfunktion
, so folgt für die
Umkehrfunktion 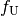 :
: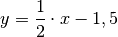
Bildet man nach dem gleichen Prinzip erneut die Umkehrfunktion einer Umkehrfunktion, so erhält man wieder die ursprüngliche Funktion zurück.
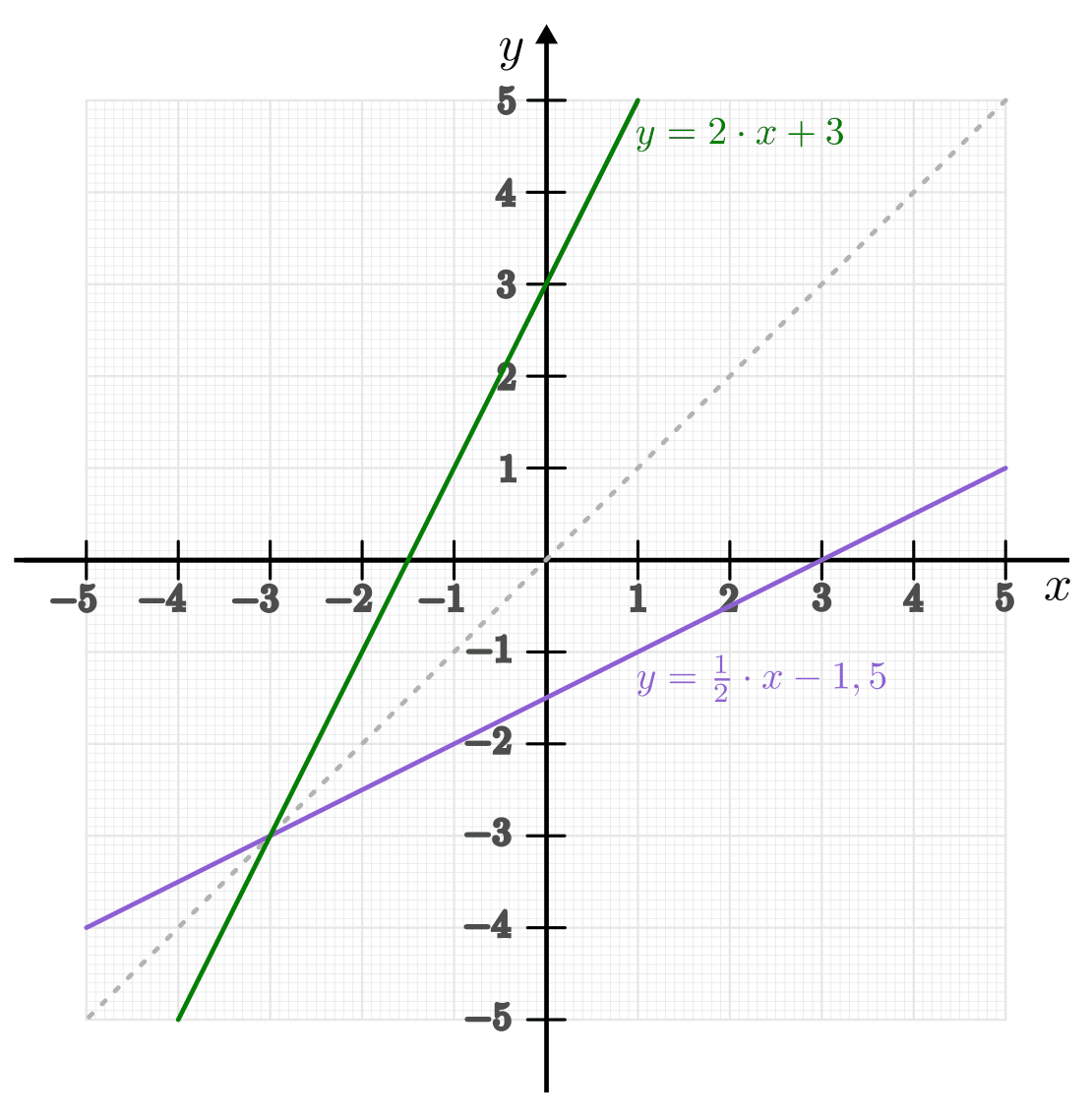
Im gleichen Koordinatensystem werden eine Funktion 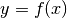 und ihre
Umkehrfunktion
und ihre
Umkehrfunktion  durch einen gleichen Funktionsgraphen
dargestellt, wenn lediglich die Benennung der
durch einen gleichen Funktionsgraphen
dargestellt, wenn lediglich die Benennung der  - und
- und  -Achse
(Argument- und Funktionswerte) ausgetauscht werden. Sollen die Bezeichnungen der
-Achse
(Argument- und Funktionswerte) ausgetauscht werden. Sollen die Bezeichnungen der
 - und
- und  -Achse hingegen bestehen bleiben, so sind die Graphen
einer Funktion und ihrer Umkehrfunktion stets achsensymmetrisch zur
Winkelhalbierenden des ersten und dritten Quadranten.
-Achse hingegen bestehen bleiben, so sind die Graphen
einer Funktion und ihrer Umkehrfunktion stets achsensymmetrisch zur
Winkelhalbierenden des ersten und dritten Quadranten.
Monotonie und Beschränktheit¶
Die Untersuchung einer Funktion auf Monotonie, Beschränktheit, Grenzwerte und Stetigkeit ermöglicht es im Bereich der Analysis, weiter reichende Aussagen über die Funktion, beispielsweise das Aussehen des Funktionsgraphen, zu treffen.
Monotonie
In gleicher Weise wie bei Zahlenfolgen stellt auch bei Funktionen die Monotonie eine wichtige charakteristische Eigenschaft einer Funktion dar.
Gilt für alle Elemente 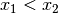 aus dem Definitionsbereich einer
Funktion auch
aus dem Definitionsbereich einer
Funktion auch 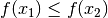 , so heißt die Funktion monoton steigend.
Entsprechend heißt eine Funktion monoton fallend, wenn für die Funktionswerte
aller
, so heißt die Funktion monoton steigend.
Entsprechend heißt eine Funktion monoton fallend, wenn für die Funktionswerte
aller 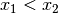 die Bedingung
die Bedingung 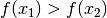 gilt. Bei einer
konstanten Funktion sind die Funktionswerte
gilt. Bei einer
konstanten Funktion sind die Funktionswerte  für alle
für alle  konstant.
konstant.
Es gilt somit für jede Funktion  und
und 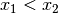 :
:
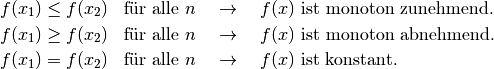
Gilt bei der obigen Unterscheidung anstelle der Kleiner-Gleich-Relation
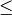 die Kleiner-Relation
die Kleiner-Relation 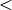 beziehungsweise anstelle der
Größer-Gleich-Relation
beziehungsweise anstelle der
Größer-Gleich-Relation 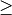 die Größer-Relation
die Größer-Relation 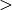 , so nennt man
die Funktion streng monoton ab- beziehungsweise zunehmend. Jede streng monoton
steigende Funktion ist bijektiv und somit umkehrbar; die Umkehrfunktion hat
dabei die gleiche Monotonie wie die ursprüngliche Funktion.
, so nennt man
die Funktion streng monoton ab- beziehungsweise zunehmend. Jede streng monoton
steigende Funktion ist bijektiv und somit umkehrbar; die Umkehrfunktion hat
dabei die gleiche Monotonie wie die ursprüngliche Funktion.
Beschränktheit
Eine Funktion  wird beschränkt genannt, wenn es zwei reelle Zahlen
wird beschränkt genannt, wenn es zwei reelle Zahlen
 und
und 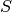 gibt, so dass alle Funktionswerte
gibt, so dass alle Funktionswerte 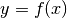 zwischen beiden begrenzenden Zahlen liegen, wenn also gilt:
zwischen beiden begrenzenden Zahlen liegen, wenn also gilt:

Hierbei wird  als untere Schranke und
als untere Schranke und  als obere Schranke
der Funktion bezeichnet.
als obere Schranke
der Funktion bezeichnet.
Eine Funktion kann in einem bestimmten Bereich auch nur einseitig eine untere
oder eine obere Schranke aufweisen. Beispielsweise gilt für alle Werte der
Funktion 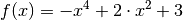 die Ungleichung
die Ungleichung 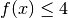 , so dass jede Zahl
, so dass jede Zahl  eine obere Schranke der Funktion darstellt.
Es lässt sich jedoch keine untere Schranke für die gleiche Funktion definieren,
da sie im negativen Bereich betraglich unendlich große Werte annimmt.
eine obere Schranke der Funktion darstellt.
Es lässt sich jedoch keine untere Schranke für die gleiche Funktion definieren,
da sie im negativen Bereich betraglich unendlich große Werte annimmt.
Hat eine Funktion in einem bestimmten Bereich weder eine obere noch eine untere Schranke, so heißt die Funktion in diesem Bereich unbeschränkt.
Grenzwerte einer Funktion¶
Die Werte einer Funktion können sich – abhängig vom Funktionstyp – ebenso wie
die Werte einer Zahlenfolge mit zunehmenden  -Werten einem bestimmten
Zahlenwert annähern. Eine Funktion besitzt genau dann einen solchen Grenzwert,
wenn sie monoton und beschränkt ist.
-Werten einem bestimmten
Zahlenwert annähern. Eine Funktion besitzt genau dann einen solchen Grenzwert,
wenn sie monoton und beschränkt ist.
Grenzwerte für 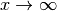 und
und 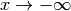
Grenzwerte von Funktionen werden ebenfalls in sehr ähnlicher Weise wie
Grenzwerte von Folgen definiert. Während
jedoch der „Definitionsbereich“ von Folgen auf die natürlichen Zahlen beschränkt
ist und somit nur ein Grenzwert für 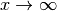 existieren kann,
können die
existieren kann,
können die  -Werte von Funktionen sowohl im positiven wie auch im
negativen Zahlenbereich unendlich groß werden; es lässt sich daher ein Grenzwert
sowohl für
-Werte von Funktionen sowohl im positiven wie auch im
negativen Zahlenbereich unendlich groß werden; es lässt sich daher ein Grenzwert
sowohl für 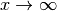 wie auch für
wie auch für 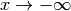 definieren.
definieren.
Ein Grenzwert einer Funktion für 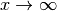 existiert genau dann, wenn
sich für immer größere
existiert genau dann, wenn
sich für immer größere  -Werte die zugehörigen
-Werte die zugehörigen  -Werte immer
mehr an einen bestimmten Wert
-Werte immer
mehr an einen bestimmten Wert 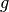 annähern. Dies ist genau dann der Fall,
wenn für alle
annähern. Dies ist genau dann der Fall,
wenn für alle  -Werte ab einer gewissen Zahl
-Werte ab einer gewissen Zahl  das
Konvergenzkriterium erfüllt ist, also die
Differenz von
das
Konvergenzkriterium erfüllt ist, also die
Differenz von 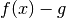 beliebig klein wird. Für jeden noch so kleinen
Wert
beliebig klein wird. Für jeden noch so kleinen
Wert  muss also gelten:
muss also gelten:
(1)¶
Anschaulich besagt diese Bedingung, dass man sich einen beliebig dünnen
„Schlauch“ (eine so genannte  -Umgebung) um den Grenzwert
-Umgebung) um den Grenzwert
 herum denken kann und dann alle Funktionswerte ab einem bestimmten
herum denken kann und dann alle Funktionswerte ab einem bestimmten
 -Wert innerhalb dieser Umgebung liegen müssen.[8]
-Wert innerhalb dieser Umgebung liegen müssen.[8]
Existiert ein Grenzwert 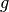 einer Funktion für beliebig große
negative beziehungsweise positive
einer Funktion für beliebig große
negative beziehungsweise positive  -Werte, so schreibt man:
-Werte, so schreibt man:
(2)¶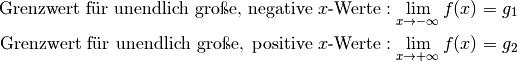
Existiert für eine Funktion  einer der beiden obigen Grenzwerte, so
nennt man die Funktion „konvergent“ für
einer der beiden obigen Grenzwerte, so
nennt man die Funktion „konvergent“ für 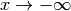 beziehungsweise
beziehungsweise
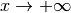 . Ebenso ist es möglich, dass eine Funktion keinen
Grenzwert für
. Ebenso ist es möglich, dass eine Funktion keinen
Grenzwert für  besitzt; in diesem Fall nennt man
sie divergent.
besitzt; in diesem Fall nennt man
sie divergent.
Beispiele:
Die Funktion
 (eine so genannte „Hyperbelfunktion“)
ist für
(eine so genannte „Hyperbelfunktion“)
ist für 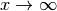 konvergent zum Grenzwert Null. Für
konvergent zum Grenzwert Null. Für
 ist der Grenzwert ebenfalls gleich Null. Es gilt
also:
ist der Grenzwert ebenfalls gleich Null. Es gilt
also: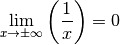
Die Funktion
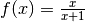 ist für
ist für 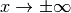 konvergent zum Grenzwert
konvergent zum Grenzwert 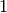 . Es gilt also:
. Es gilt also: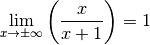
Die Funktion
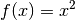 (eine „Parabel“) ist divergent, sie hat keinen
Grenzwert.
(eine „Parabel“) ist divergent, sie hat keinen
Grenzwert.
Werden die Funktionswerte einer divergierenden Funktion mit zunehmenden
 -Werten unendlich groß, so bezeichnet man
-Werten unendlich groß, so bezeichnet man 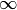 als
„uneigentlichen“ Grenzwert – tatsächlich existiert in diesem Fall keine
bestimmte Zahl
als
„uneigentlichen“ Grenzwert – tatsächlich existiert in diesem Fall keine
bestimmte Zahl 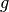 als obere Schranke, wie sie für einen Grenzwert
eigentlich existieren muss.
als obere Schranke, wie sie für einen Grenzwert
eigentlich existieren muss.
Grenzwert für 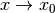
Grenzwerte von Funktionen können nicht nur für unendlich große negative
beziehungsweise positive  -Werte betrachtet werden; es ist ebenso
möglich zu prüfen, ob ein Grenzwert existiert, wenn sich die
-Werte betrachtet werden; es ist ebenso
möglich zu prüfen, ob ein Grenzwert existiert, wenn sich die  -Werte
einem frei wählbaren Wert
-Werte
einem frei wählbaren Wert  annähern. Existiert ein solcher Grenzwert
annähern. Existiert ein solcher Grenzwert
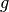 , so schreibt man:
, so schreibt man:
(3)¶
Ist die Funktion  an der Stelle
an der Stelle  definiert, so ist ihr
Grenzwert an dieser Stelle gleich ihrem Funktionswert, es gilt also
definiert, so ist ihr
Grenzwert an dieser Stelle gleich ihrem Funktionswert, es gilt also
 für
für 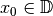 . Der obige Grenzwert kann
allerdings auch dann existieren, wenn die Funktion an der Stelle
. Der obige Grenzwert kann
allerdings auch dann existieren, wenn die Funktion an der Stelle  nicht definiert ist. Vor allem an den Grenzen des Definitionsbereichs
nicht definiert ist. Vor allem an den Grenzen des Definitionsbereichs
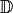 (beispielsweise an Definitionslücken) werden Funktionen
deshalb häufig auf mögliche Grenzwerte untersucht.
(beispielsweise an Definitionslücken) werden Funktionen
deshalb häufig auf mögliche Grenzwerte untersucht.
Sofern möglich, nähert man dazu die  -Werte der Stelle
-Werte der Stelle  sowohl von links als auch von rechts an; man untersucht also das Verhalten der
Funktion an den Stellen
sowohl von links als auch von rechts an; man untersucht also das Verhalten der
Funktion an den Stellen 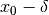 und
und  , wobei
, wobei
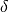 eine möglichst kleine Zahl ist. Man bildet also folgende
Grenzwerte:
eine möglichst kleine Zahl ist. Man bildet also folgende
Grenzwerte:
![g_{\mathrm{-}} = \lim_{\substack{x \to (x_0-h), \\ h \to 0}} \big(f(x)\big)
\\[4pt]
g_{\mathrm{+}} = \lim_{\substack{x \to (x_0+h), \\ h \to 0}} \big(f(x)\big)](../_images/math/b8f0dd144a7bac84c4c1caa19df2b2286d8e761f.png)
Entsprechend bezeichnet man die beiden zugehörigen Grenzwerte 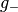 und
und
 als „linksseitig“ beziehungsweise „rechtsseitig“.
als „linksseitig“ beziehungsweise „rechtsseitig“.
Rechenregeln für Grenzwerte
Für das Rechnen mit Grenzwerten gibt es folgende Rechenregeln:
(4)¶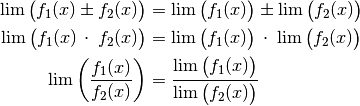
Bei der Division zweier Funktionen beziehungsweise Grenzwerte muss dabei darauf
geachtet werden, dass nicht durch Null dividiert wird, es muss also
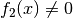 für alle
für alle  sowie
sowie 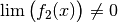 gelten. Ist im Speziellen
gelten. Ist im Speziellen 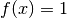 und
und 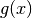 eine Funktion mit
dem Grenzwert
eine Funktion mit
dem Grenzwert  für
für 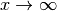 , so gilt:
, so gilt:
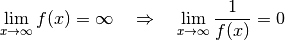
Gilt zudem für drei Funktionen 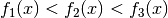 und sind die
Grenzwerte
und sind die
Grenzwerte 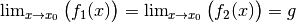 der kleinsten und größten Funktion identisch, so gilt
dies auch für den Grenzwert der „mittleren“ Funktion.
der kleinsten und größten Funktion identisch, so gilt
dies auch für den Grenzwert der „mittleren“ Funktion.
Stetigkeit¶
Man bezeichnet eine Funktion an einer Stelle 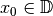 als
stetig, wenn an dieser Stelle der linksseitige Grenzwert
als
stetig, wenn an dieser Stelle der linksseitige Grenzwert 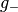 , der
rechtsseitige Grenzwert
, der
rechtsseitige Grenzwert 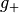 und der Funktionswert
und der Funktionswert 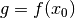 übereinstimmen. Eine Funktion wird (global) stetig genannt, wenn die
Stetigkeitsbedingung für alle
übereinstimmen. Eine Funktion wird (global) stetig genannt, wenn die
Stetigkeitsbedingung für alle  -Werte des Definitionsbereichs erfüllt
ist.
-Werte des Definitionsbereichs erfüllt
ist.
Anschaulich bedeutet Stetigkeit, dass der Graph einer Funktion keine „Sprünge“
macht, also entlang des Definitionsbereichs als eine durchgezogene Linie (ohne
Absetzen des Schreibstifts) gezeichnet werden kann. Dies ist bei sehr vielen
Funktionen der Fall, beispielsweise bei allen ganz-rationalen Funktionen, der
Sinus- beziehungsweise Cosinusfunktion. Auch die Tangens- und Hyperbelfunktion
 sind stetig, da sich ihre Funktionswerte nur an den
jeweils nicht definierten Stellen (Definitionslücken) sprunghaft ändern. Auch
die Kombination zweier oder mehrerer stetiger Funktionen mittels den
Grundrechenarten Addition, Subtraktion, Multiplikation oder Division ungleich
Null ergibt wieder eine stetige Funktion.
sind stetig, da sich ihre Funktionswerte nur an den
jeweils nicht definierten Stellen (Definitionslücken) sprunghaft ändern. Auch
die Kombination zweier oder mehrerer stetiger Funktionen mittels den
Grundrechenarten Addition, Subtraktion, Multiplikation oder Division ungleich
Null ergibt wieder eine stetige Funktion.
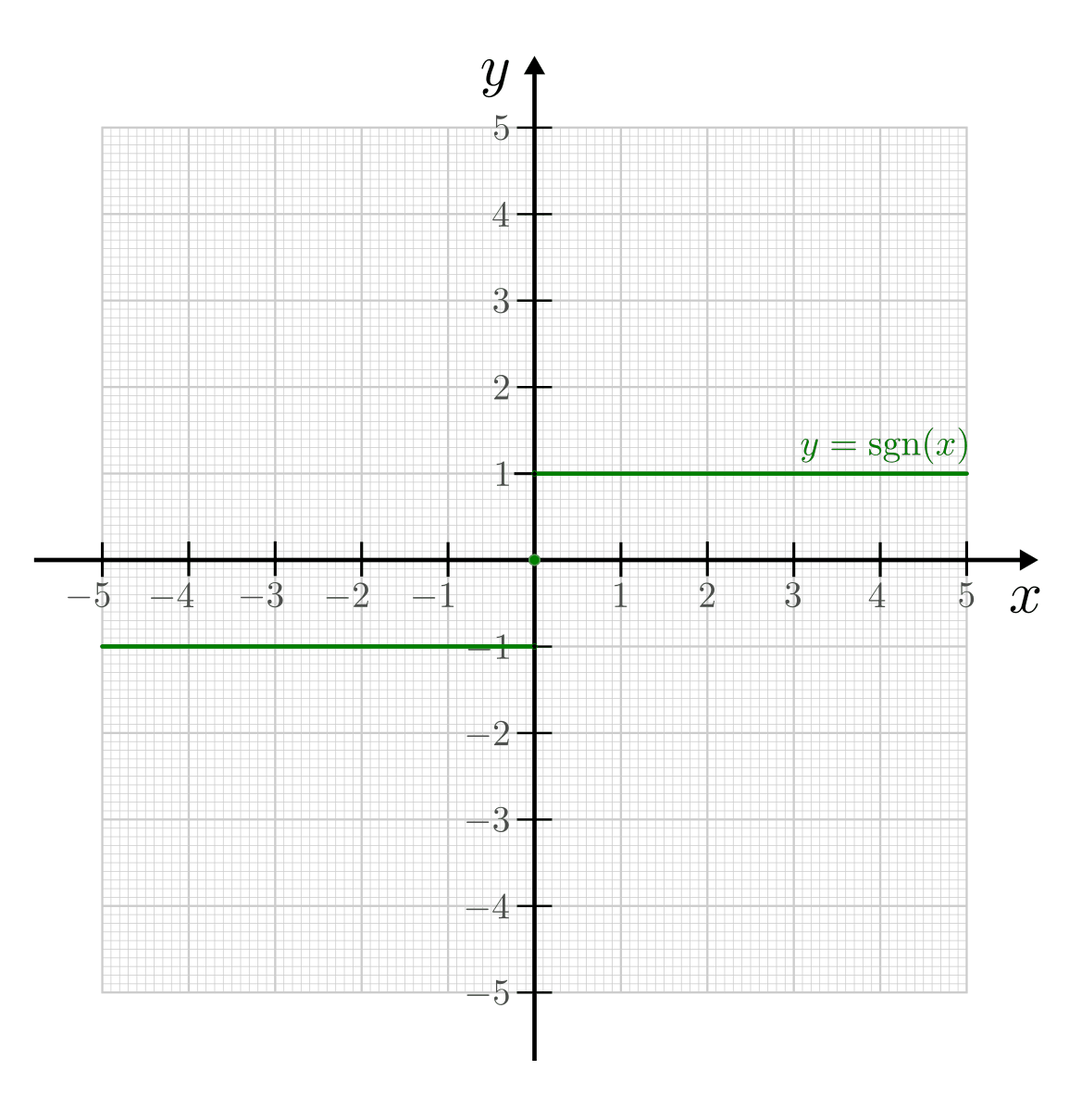
Ein anschauliches Beispiel für eine lokal, aber nicht global stetige Funktion ist die so genannte Signum-Funktion (auch Vorzeichenfunktion genannt). Sie ist abschnittsweise folgendermaßen definiert:
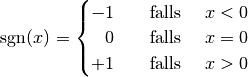
Die Signum-Funktion ist an allen Stellen bis auf  (lokal) stetig.
An dieser Stelle jedoch stimmen ihr linksseitiger Grenzwert
(lokal) stetig.
An dieser Stelle jedoch stimmen ihr linksseitiger Grenzwert
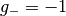 , ihr Funktionswert
, ihr Funktionswert 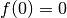 und ihr
rechtsseitiger Grenzwert
und ihr
rechtsseitiger Grenzwert  nicht überein.
nicht überein.
Zwischenwertsatz und Extremwertsatz
Ist eine Funktion 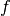 in einem Intervall stetig, so ist sie dort auch
begrenzt. Es existieren also eine untere Schranke
in einem Intervall stetig, so ist sie dort auch
begrenzt. Es existieren also eine untere Schranke  und eine obere
Schranke
und eine obere
Schranke 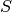 , so dass
, so dass  für alle
für alle  -Werte
des Intervalls gilt.
-Werte
des Intervalls gilt.
Ist eine Funktion 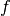 in einem abgeschlossenen Intervall
in einem abgeschlossenen Intervall ![[a\,;\,b]](../_images/math/b974d65e037edcf47dc94c7cf2b98d55e7b855bb.png) stetig, so gilt der so genannte Extremwertsatz: In diesem Fall lassen sich stets
zwei Funktionswerte
stetig, so gilt der so genannte Extremwertsatz: In diesem Fall lassen sich stets
zwei Funktionswerte 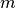 und
und 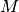 finden, so dass
finden, so dass 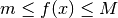 gilt. Der Wert
gilt. Der Wert 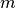 wird dabei als Minimum, der Wert
wird dabei als Minimum, der Wert 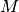 als
Maximum der Funktion
als
Maximum der Funktion 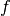 im Intervall
im Intervall ![[a\,;\,b]](../_images/math/b974d65e037edcf47dc94c7cf2b98d55e7b855bb.png) bezeichnet.
bezeichnet.
Eine in einem abgeschlossenen Intervall ![[a\,;\,b]](../_images/math/b974d65e037edcf47dc94c7cf2b98d55e7b855bb.png) stetige Funktion
stetige Funktion
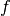 nimmt zudem jeden Wert zwischen
nimmt zudem jeden Wert zwischen 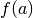 und
und 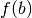 mindestens einmal an. Diese insbesondere für die numerische Berechnung von
Nullstellen wichtige Tatsache wird „Zwischenwertsatz“ genannt.
mindestens einmal an. Diese insbesondere für die numerische Berechnung von
Nullstellen wichtige Tatsache wird „Zwischenwertsatz“ genannt.
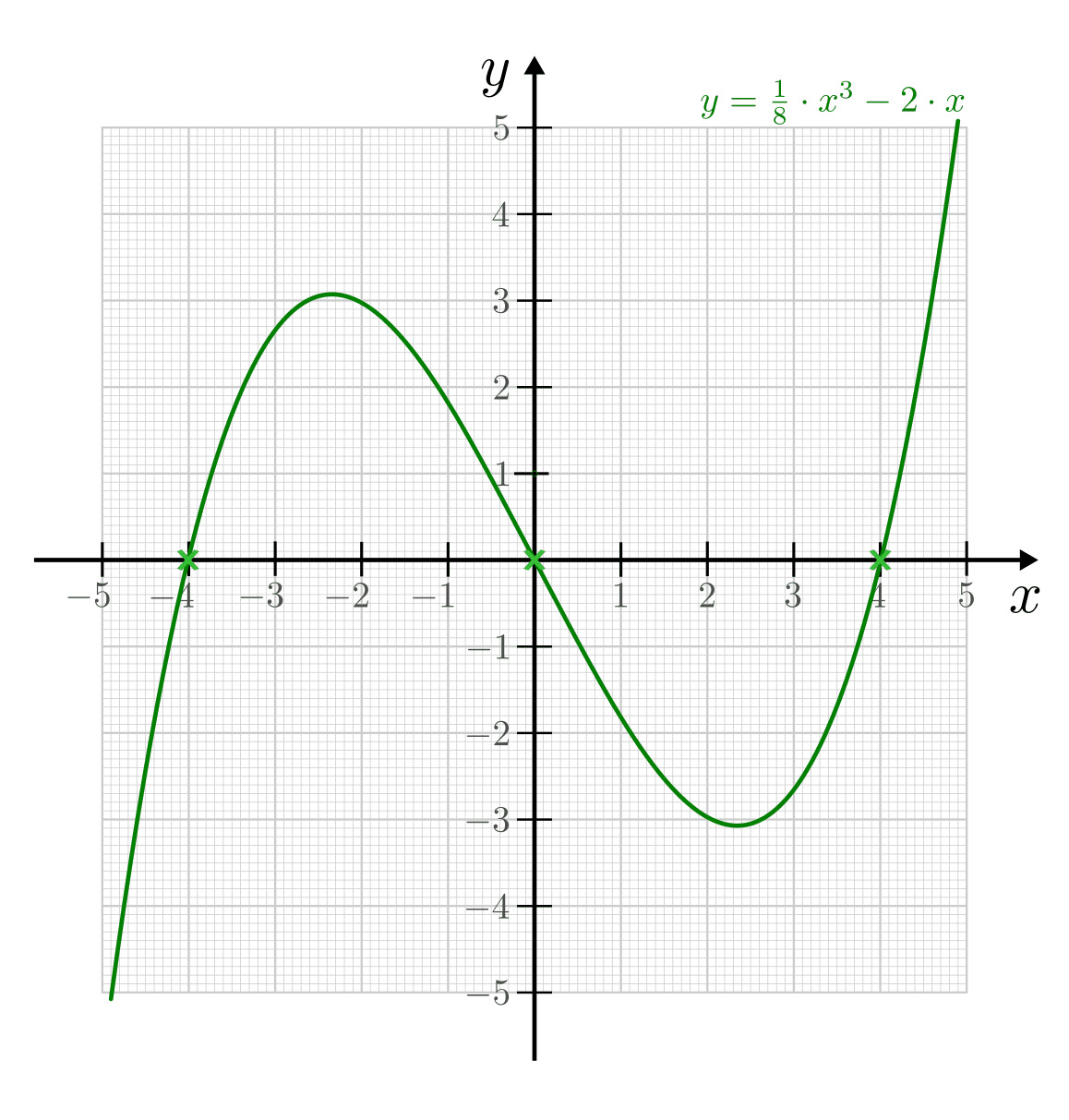
Nullstellen¶
Als eine Nullstelle wird ein Ausgangswert  einer Funktion bezeichnet,
für den der zugehörige Funktionswert
einer Funktion bezeichnet,
für den der zugehörige Funktionswert 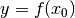 den Wert Null annimmt:
den Wert Null annimmt:

Die Nullstellen einer Funktion lassen sich bestimmen, indem man in die implizite
oder explizite Darstellung der Funktion für  den Wert Null einsetzt
und die sich ergebende Gleichung mit algebraischen Methoden nach
den Wert Null einsetzt
und die sich ergebende Gleichung mit algebraischen Methoden nach  auflöst. Je nach Art der Funktion ist es möglich, dass diese mehrere, eine
oder auch keine Nullstelle besitzt.
auflöst. Je nach Art der Funktion ist es möglich, dass diese mehrere, eine
oder auch keine Nullstelle besitzt.
Zeichnet man eine Funktion als Graph in einem Koordinatensystem ein, so stellen
Nullstellen Schnitt- oder Berührungspunkte mit der  -Achse dar.
-Achse dar.
Schnittpunkte zweier Funktionen
Eng verbunden mit der Bestimmung von Nullstellen ist die Bestimmung von
Schnittstellen zweier oder mehrerer Funktionen. Betrachtet man zwei Funktionen
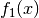 und
und  , so kann man prüfen, für welche
, so kann man prüfen, für welche
 -Werte aus dem gemeinsamen Definitionsbereich
-Werte aus dem gemeinsamen Definitionsbereich 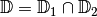 die Werte der Funktionen übereinstimmen, für
welche Ausgangswerte
die Werte der Funktionen übereinstimmen, für
welche Ausgangswerte 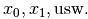 also die
Bedingung
also die
Bedingung  gilt. Das Lösen dieser Gleichung stimmt formal
mit der Bestimmung der Nullstelle von
gilt. Das Lösen dieser Gleichung stimmt formal
mit der Bestimmung der Nullstelle von  überein:
überein:
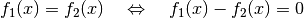
Existieren ein oder mehrere Schnittpunkte, so sind an den entsprechenden Stellen
die Funktionswerte von 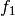 und
und 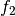 üblicherweise nicht gleich
Null. Man erhält die zugehörigen
üblicherweise nicht gleich
Null. Man erhält die zugehörigen  -Werte der Schnittpunkte, indem man
die beim Lösen der obigen Gleichung gefundenen
-Werte der Schnittpunkte, indem man
die beim Lösen der obigen Gleichung gefundenen  -Werte in eine der
beiden Funktionen einsetzt.
-Werte in eine der
beiden Funktionen einsetzt.
Verknüpfung und Verkettung von Funktionen¶
Aus den elementaren Funktionen, die in den nächsten Abschnitten näher beschrieben werden, lassen sich weitere Funktionen zusammensetzen. Dies ist auf zweierlei Arten möglich:
Bei einer so genannten Verknüpfung werden zwei Funktionen durch eine der vier Grundrechenarten miteinander verbunden. Das Ergebnis einer so zusammengesetzten Funktion erhält man, indem man zunächst die Werte der beiden Funktionen berechnet und diese dann mit der entsprechenden Grundrechenart verknüpft. Schrittweise lassen sich so auch mehrere Funktionen miteinander verknüpfen, wobei auf die Auswertungsreihenfolge der Verknüpfungen (Multiplikation beziehungsweise Division vor Addition beziehungsweise Subtraktion) zu achten ist.
Allgemein hat eine verknüpfte Funktion somit folgende Form:
(5)¶
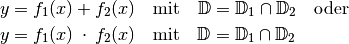
Einfache Sonderfälle von Gleichung (5) ergeben sich hierbei, wenn eine der beiden Funktionen konstant ist. Hierbei entstehen folgende Funktionen:
(6)¶
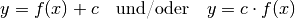
Im ersten Fall wird zu jedem Funktionswert die Konstante
 addiert
(beziehungsweise subtrahiert, wenn
addiert
(beziehungsweise subtrahiert, wenn 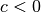 ist). Bei einer graphischen
Darstellung wird der Funktionsgraph dadurch um
ist). Bei einer graphischen
Darstellung wird der Funktionsgraph dadurch um  Einheiten in
vertikaler Richtung verschoben (nach oben für
Einheiten in
vertikaler Richtung verschoben (nach oben für 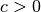 , nach unten für
, nach unten für
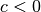 ).
).Im zweiten Fall wird der Funktionswert mit einer Konstanten
 multipliziert. Dadurch wird der Funktionsgraph im Fall
multipliziert. Dadurch wird der Funktionsgraph im Fall  vertikal gestaucht, im Fall
vertikal gestaucht, im Fall 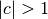 vertikal gestreckt. Ist
vertikal gestreckt. Ist 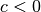 ,
so wird der Funktionsgraph (wie bei einer zentrischen Streckung) an der
,
so wird der Funktionsgraph (wie bei einer zentrischen Streckung) an der  -Achse gespiegelt.
-Achse gespiegelt.Bei einer so genannten Verkettung werden zwei Funktionen „hintereinander“ ausgeführt, der Funktionswert der ersten Funktion wird also als Ausgangswert der zweiten Funktion verwendet. Dies ist im Allgemeinen nur dann möglich, wenn der Wertebereich der ersten Funktion eine Teilmenge des Definitionsbereichs der zweiten Funktion ist.
Allgemein hat eine verkettete Funktion somit folgende Form:
(7)¶
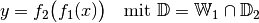
Dabei wird
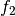 als äußere und
als äußere und 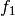 als innere Funktion
bezeichnet. Ähnlich wie bei der Auswertung von Termen in Klammern wird
zunächst der Wert der inneren Funktion
als innere Funktion
bezeichnet. Ähnlich wie bei der Auswertung von Termen in Klammern wird
zunächst der Wert der inneren Funktion 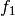 berechnet, und dieser
anschließend, sofern erlaubt, als Argument für die äußere Funktion
berechnet, und dieser
anschließend, sofern erlaubt, als Argument für die äußere Funktion
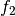 eingesetzt.
eingesetzt.
Bei der Verkettung zweier Funktionen ist die Reihenfolge der Verkettung zu
beachten: Ist beispielsweise 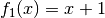 und
und 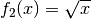 , so ist
, so ist 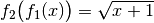 , während
, während
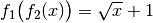 ergibt.
ergibt.
Anmerkungen:
| [1] | In den folgenden Abschnitten werden nur Funktionen untersucht, deren
Werte von nur einer (unabhängigen) Variablen  abhängig sind. Bei
der Analysis von Funktionen mit mehreren Veränderlichen kann, sofern alle
Variablen unabhängig voneinander sind, der Einfluss jeder Größe einzeln
untersucht werden. abhängig sind. Bei
der Analysis von Funktionen mit mehreren Veränderlichen kann, sofern alle
Variablen unabhängig voneinander sind, der Einfluss jeder Größe einzeln
untersucht werden. |
| [2] | Die Untersuchung komplexwertiger Funktionen, die erst im Mathematik-Studium behandelt wird, bezeichnet man als „Funktionentheorie“. |
| [3] | Konkret liegt ein Punkt somit genau dann auf der Kurve einer Funktion,
wenn seine Koordinaten die Funktionsgleichung erfüllen. Erfüllen das
Zahlenpaar  eines Punktes die Funktionsgleichung nicht, so
liegt er entsprechend außerhalb des Funktionsgraphen. eines Punktes die Funktionsgleichung nicht, so
liegt er entsprechend außerhalb des Funktionsgraphen. |
| [4] | Hierbei entspricht die Zeit  der Variablen. Für zeitabhängige
Funktionswerte wird daher häufig auch der Variablen. Für zeitabhängige
Funktionswerte wird daher häufig auch 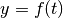 geschrieben. geschrieben. |
| [5] | Bisweilen wird anstelle der Schreibweise 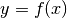 auch die Kurzform auch die Kurzform
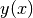 verwendet, um die Abhängigkeit der Variablen verwendet, um die Abhängigkeit der Variablen  von der
Variablen von der
Variablen  zum Ausdruck zu bringen. zum Ausdruck zu bringen. |
| [6] | Somit ist jede bijektive Funktion sowohl surjektiv als auch injektiv. |
| [7] | Beispielsweise kann die (surjektive) Funktion Entsprechend kann die (injektive) Funktion |
| [8] | Ebenso kann man für jede monotone Zahlenfolge 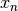 aus den Werten
des Definitionsbereichs die Folge der zugehörigen Funktionswerte betrachten.
Hat eine Funktion beispielsweise für aus den Werten
des Definitionsbereichs die Folge der zugehörigen Funktionswerte betrachten.
Hat eine Funktion beispielsweise für 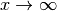 den Grenzwert den Grenzwert
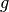 , so hat auch jede frei wählbare Folge , so hat auch jede frei wählbare Folge 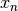 die Folge die Folge
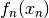 der zugehörigen Funktionswerte den gleichen Grenzwert der zugehörigen Funktionswerte den gleichen Grenzwert
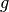 . . |
Hinweis
Zu diesem Abschnitt gibt es Übungsaufgaben.


 .
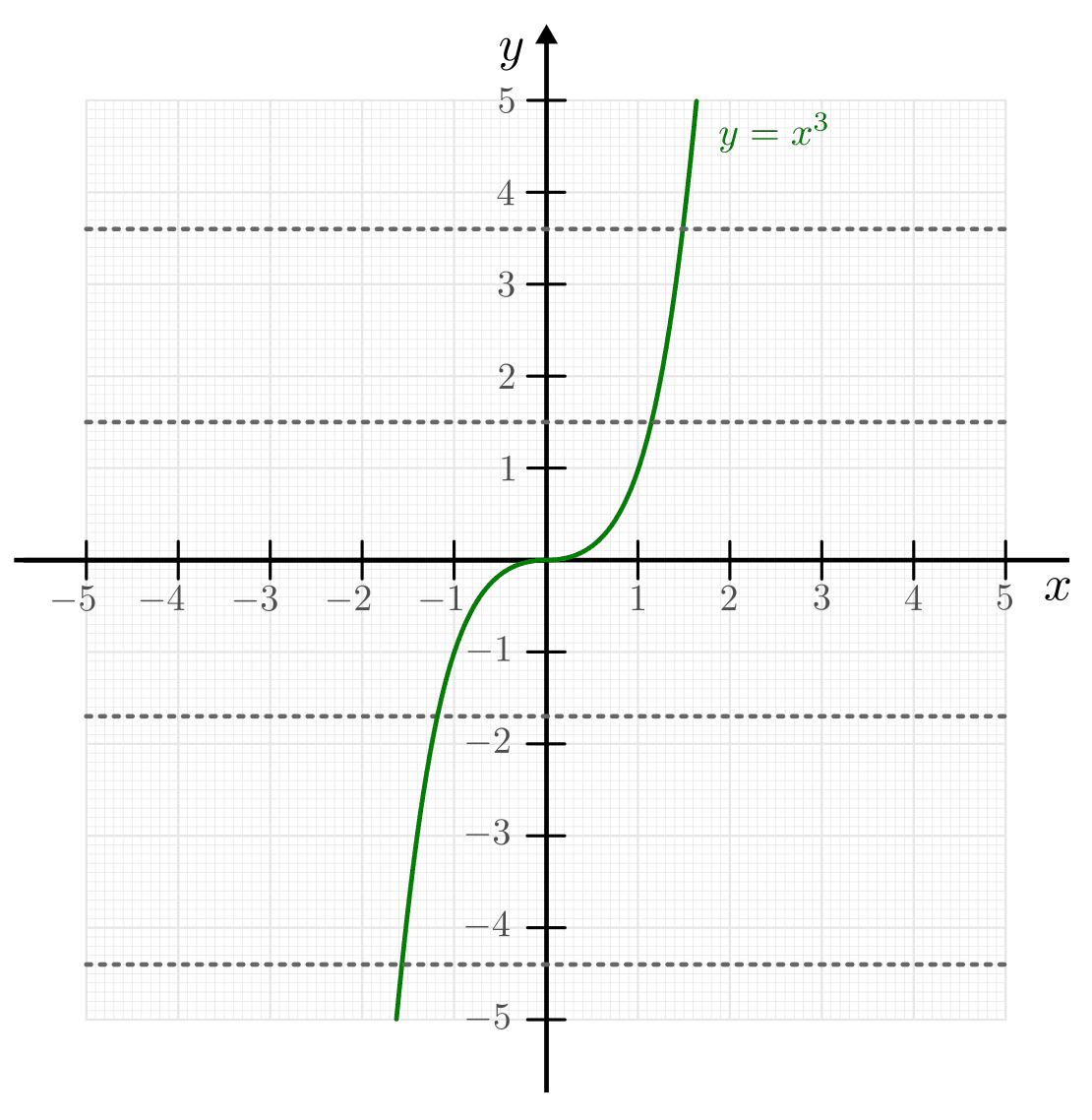
.
 .
.
 und ihrer Umkehrfunktion
und ihrer Umkehrfunktion
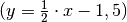 .
.
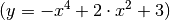 .
.
 .
.
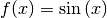 mit
mit ![\mathbb{W} =
[-1 ;\; +1]](../_images/math/adfed1c45fcda927696eed51fbc1528375c6de29.png) durch eine Einschränkung des Definitionsbereichs auf
durch eine Einschränkung des Definitionsbereichs auf
![\mathbb{D} = [-\pi ;\; +\pi]](../_images/math/603ef7f38c7baf4d7e11f787bedcf797c232d4e8.png) zu einer bijektiven Funktion
gemacht werden.
zu einer bijektiven Funktion
gemacht werden.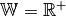 zu einer bijektiven Funktion gemacht werden.
zu einer bijektiven Funktion gemacht werden.