Rationale Funktionen¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Rationale Funktionen.
Lineare Funktionen
Als Wertetabelle für die Funktion
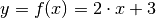 erhält man:
erhält man:
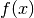
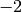
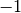
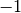
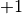
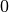
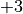
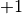
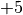
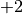
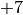
Zeichnet man diese Werte in ein kartesisches Koordinatensystem ein, so ergibt sich folgender Funktionsgraph:
Ist der Definitions- beziehungsweise Wertebereich der Funktion
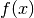 gleich der Menge
gleich der Menge 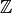 der ganzen Zahlen, so erhält man nur die
einzelnen Punkte als Funktionsgraph; sind der Definitions- beziehungsweise
Wertebereich hingegen gleich der Menge
der ganzen Zahlen, so erhält man nur die
einzelnen Punkte als Funktionsgraph; sind der Definitions- beziehungsweise
Wertebereich hingegen gleich der Menge 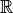 der reellen Zahlen,
so erhält man als Funktionsgraph eine Gerade.
der reellen Zahlen,
so erhält man als Funktionsgraph eine Gerade.
Der Steigungsfaktor
 einer linearen Funktion gibt an, um wie viele
Längeneinheiten
einer linearen Funktion gibt an, um wie viele
Längeneinheiten 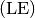 sich der Funktionswert
sich der Funktionswert 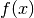 ändert,
wenn der
ändert,
wenn der  -Wert um
-Wert um ![\unit[1]{LE}](../../_images/math/8bef92f629f47c9ac4abf6ccd6c9a8e35dacbbff.png) erhöht wird.
erhöht wird.Im konkreten Fall verbindet die Gerade die Punkte
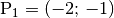 und
und 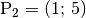 . Der Funktionswert von
. Der Funktionswert von 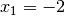 beträgt also
beträgt also 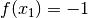 , der Funktionswert von
, der Funktionswert von 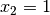 hingegen
hingegen
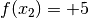 :
:
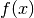
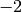
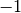


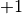
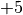
Zwischen
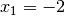 und
und 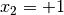 liegen insgesamt
liegen insgesamt
![\unit[3]{LE}](../../_images/math/15d166f46271eacfe39bf81e1a66e1ab542cef2b.png) ; zwischen
; zwischen 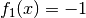 und
und 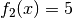 hingegen
hingegen
![\unit[6]{LE}](../../_images/math/db0a4cbac6973957974a58da76f0530275b87c04.png) . Für den Steigungsfaktor
. Für den Steigungsfaktor  ergibt sich damit:
ergibt sich damit: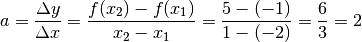
Die zur Geraden gehörende lineare Funktion hat somit den Steigungsfaktor
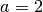 .
.
