Volumen bei Rotation um die 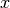 -Achse¶
-Achse¶
Bei dieser Aufgabe geht es um eine Volumensberechnung beziehungsweise um die Berechnung eines bestimmten Integrals
Aufgabe:
Das Volumen eines Rotationskörpers soll berechnet werden. Gegeben sind die
erzeugende Funktion, die Untergrenze und die Obergrenze des Intervalls. Die
Rotation soll um die 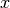 -Achse erfolgen. Die Aufgabe soll für die
Funktion
-Achse erfolgen. Die Aufgabe soll für die
Funktion  gelöst werden, wobei die
Untergrenze bei
gelöst werden, wobei die
Untergrenze bei  und die Obergrenze bei
und die Obergrenze bei  liegen soll.
liegen soll.
Lösung:
Der Graph der Funktion  kann mit Hilfe von
numpy und der matplotlib geplottet werden:
kann mit Hilfe von
numpy und der matplotlib geplottet werden:
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
# Wertereihen erzeugen:
x = np.arange(start=1,stop=5, step=0.01)
y = x**2 + x + 1/x
# Funktion plotten:
plt.plot(x,y)
# Layout anpassen:
plt.axis([0,6,0,35])
plt.xlabel("$x$")
plt.ylabel("$y$")
plt.grid(True)
plt.text(3.5, 30, "$f(x)=x^2 + x + 1/x$")
plt.show()
Das Ergebnis sieht folgendermaßen aus:
Um das Volumen des aus  bei Rotation um die
bei Rotation um die 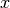 -Achse
entstehenden Rotionskörpers zu berechnen, kann man sich diesen aus lauter
winzig schmalen (Zylinder-)Scheiben zusammengesetzt denken. Jede dieser Scheiben
hat als Radius den Wert
-Achse
entstehenden Rotionskörpers zu berechnen, kann man sich diesen aus lauter
winzig schmalen (Zylinder-)Scheiben zusammengesetzt denken. Jede dieser Scheiben
hat als Radius den Wert  , als Höhe den Wert
, als Höhe den Wert  und als Volumen somit
und als Volumen somit  . Alle diese infinitesimalen Volumina müssen aufsummiert werden,
was folgendem Integral entspricht:
. Alle diese infinitesimalen Volumina müssen aufsummiert werden,
was folgendem Integral entspricht:

Dieses Integral kann mittels Sympy berechnet werden. Der Code dazu lautet folgendermaßen:
import sympy as sy
# Sympy-Variablen initiieren:
x = sy.S( 'x' )
a, b = sy.S( [1, 5] )
# Bestimmtes Integral berechnen:
sy.integrate( sy.pi * (x**2 + x + 1/x) , (x,a,b) )
# Ergebnis: 15164*pi/15
# Alternativ: Ergebnis als Fließkommazahl ausgeben:
sy.integrate( sy.pi * (x**2 + x + 1/x) , (x,a,b) ).evalf()
# Ergebnis: 3175.94073326904
Das Volumen des Rotationskörpers beträgt somit rund  Volumeneinheiten.
Volumeneinheiten.

