Geradliniger Flug¶
Bei dieser Aufgabe geht es darum, eine physikalische Bewegungsgleichung zu lösen.
Aufgabe:
Zwei Flugzeuge verlassen einen Flughafen zur selben Zeit in entgegengesetzte
Richtungen mit den Geschwindigkeiten ![v_1 = \unit[490]{km/h}](../../_images/math/d98a29b3e22ffbc83f4f85455f9d7a94ac010a06.png) beziehungsweise
beziehungsweise ![v_2 = \unit[368]{km/h}](../../_images/math/7b7a8b4c84956d8811d626c66a0f4e676240e93c.png) . Nach welcher Zeit
. Nach welcher Zeit  haben sie einen Abstand von
haben sie einen Abstand von ![s=\unit[3805]{km}](../../_images/math/9469d2b98aac86f0c43aa58c111bc4f31df95b8f.png) erreicht?
erreicht?
Lösung:
Die beiden Flugzeuge bewegen sich mit der Summe ihrer Geschwindigkeiten, also
mit ![v=v_1 + v_2 = \unit[858]{km/h}](../../_images/math/b86dd119e5f8bc00aaefcce9c1675459ba84588a.png) auseinander. Aus der Weg-Zeig-Formel
auseinander. Aus der Weg-Zeig-Formel
 für Bewegungen mit konstanter Geschwindigkeit lässt sich
die gesuchte Größe
für Bewegungen mit konstanter Geschwindigkeit lässt sich
die gesuchte Größe  berechnen. Der Sympy-Code dazu lautet:
berechnen. Der Sympy-Code dazu lautet:
import sympy as sy
# Sympy-Variablen initiieren:
s = sy.S( 3805 )
v = sy.S( 858 )
t = sy.S( 't' )
# Gleichung formulieren:
equation = sy.Eq( s , v * t )
# Gleichung lösen:
result = sy.solve(equation)
# Ergebnis: [3805/858]
# Ergebnis als Fließkommazahl ausgeben:
float(result[0])
# Ergebnis: 4.434731934731935
Die gesuchte Zeit beträgt somit rund ![\unit[4,435]{Stunden}](../../_images/math/3d739904cf69d072032a9e7cf88f1a0924a0068e.png) . Etwas
eleganter ist allerdings die Angabe in Stunden und Minuten. Sie kann
aus dem obigen Ergebnis folgendermaßen berechnet werden:
. Etwas
eleganter ist allerdings die Angabe in Stunden und Minuten. Sie kann
aus dem obigen Ergebnis folgendermaßen berechnet werden:
import math
result_f = float(result[0])
hours = math.floor(result_f)
# Ergebnis: 4.0
minutes = (result_f - math.floor(result_f)) * 60
# Ergebnis: 26.083916083916083
Die gesuchte Zeit beträgt somit rund  Stunden und
Stunden und  Minuten.
Minuten.

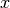 -Achse
-Achse