sympy – ein Computer-Algebra-System¶
Sympy ist ein Modul, das ein
Computer-Algebra-System für Python bereitstellt. Es kann, wenn bei der
Python-Installation das Paket python3-setuptools mit
installiert wurde, in einer Shell folgendermaßen heruntergeladen installiert
werden:
sudo easy_install3 sympy
Anschließend kann es beispielsweise mittels import sympy oder import
sympy as sy importiert werden. Im folgenden wird von letzterer Variante
ausgegangen, um Schreibarbeit zu sparen.
Im folgenden werden nur einige häufig vorkommende Funktionen von Sympy beschrieben. Eine vollständige Dokumentation findet man auf der Sympy-Projektseite.
Konstanten und mathematische Funktionen¶
Ähnlich wie im math-Modul sind auch in Sympy einige mathematische Konstanten
definiert:
sy.E |
Eulersche Zahl | 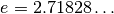 |
sy.pi |
Kreiszahl | 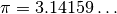 |
sy.GoldenRatio |
Goldener Schnitt | 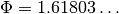 |
sy.oo |
Unendlich | 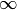 |
Ebenso sind in Sympy alle elementaren Funktionen wie sin(), cos(),
exp() usw. definiert und können in gleicher Weise wie im math-Modul
verwendet werden. Weitere hilfreiche Funktionen sind beispielsweise:
sy.Abs(x) |
Betragsfunktion |
sy.binomial(n,k) |
Binomialkoeffizient |
sy.factorial(num) |
Fakultät |
sy.fibonacci(n) |
Fibonacci-Folge (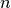 -tes Element) -tes Element) |
sy.log(x) |
Natürlicher Logarithmus (Basis  ) ) |
sy.log(x, a) |
Logarithmus zur Basis  |
Das besondere an den Sympy-Funktionen ist, dass diese nicht nur eine einzelne
Zahl bzw. eine Variable als Argument akzeptieren, sondern auch auf so genannte
„Symbole“ angewendet werden können. Mit diesem Datentyp werden in Sympy die in
der Mathematik für Variablennamen genutzten Buchstaben dargestellt.
Beispielsweise kann eine in der Mathematik typischerweise mit 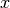 bezeichnete Variable folgendermaßen als Sympy-Symbol definiert werden:
bezeichnete Variable folgendermaßen als Sympy-Symbol definiert werden:
x = sy.S('x')
type(x)
# Ergebnis: sympy.core.symbol.Symbol
Möchte man mehrere „Symbole“ – also mehrere „mathematische“ Variablen – auf
einmal definieren, so kann die symbols()-Funktion genutzt werden, um eine
durch Leerzeichen getrennte Zeichenkette als Liste von Symbol-Bezeichnungen
zu interpretieren:
x,y,z = sy.symbols('x y z')
Bei der Festlegung von Symbolen mittels sy.S() oder sy.symbols() kann
auch als Option positive=True angegeben werden, um nicht-negative
mathematische Variablen zu definieren.
Mit diesen Symbolen kann nun gerechnet werden, ohne ihnen einen expliziten Wert zuweisen zu müssen.
Ausmultiplizieren und Vereinfachen¶
Um mathematische Terme umzuformen oder zu vereinfachen, gibt es in Sympy unter
anderem die Funktionen expand(), factor(), ratsimp() und
simplify().
Mit Hilfe der expand()-Funktion lassen sich beispielsweise binomische
Formeln explizit berechnen:
x = sy.S('x')
sy.expand( (x + 2)**5 )
# Ergebnis: x**5 + 10*x**4 + 40*x**3 + 80*x**2 + 80*x + 32
Die expand()-Funktion kann mittels der Optionen frac=True, log=True
oder trig=True auch zum Erweitern von Bruchtermen, Logarithmen oder
trigonometrischen Ausdrücken verwendet werden:
x = sy.S('x')
x1, x2 = sy.symbols('x1 x2')
sy.expand( ((x+3)/x) / (x+1) , frac=True)
# Ergebnis: (x + 3)/(x**2 + x)
sy.expand( sy.log(x**5) , log=True, force=True)
# Ergebnis: 5*log(x)
sy.expand( sy.sin(x1+x2) , trig=True)
# Ergebnis: sin(x1)*cos(x2) + sin(x2)*cos(x1)
Im letzten Beispiel wurde die Erweiterung durch die Option force=True
erzwungen, da Sympy in diesem Fall die angegebene Umformung des Terms als
ungünstig einstuft.
Umgekehrt können beispielsweise Polynome mittels der Funktion factor() in
einzelne Faktoren oder Binome zerlegt werden:
x = sy.S('x')
sy.factor( 3*x**5 + 7*x**2 )
# Ergebnis: x**2*(3*x**3 + 7)
sy.factor( x**2 + 2*x + 1 )
# Ergebnis: (x + 1)**2
Bruchterme lassen sich mittels der Funktion ratsimp() vereinfachen:
x = sy.S('x')
x1, x2 = sy.symbols('x1 x2')
sy.ratsimp( (x**2 - 9) / (x-3) )
# Ergebnis: x + 3
sy.ratsimp( 1/x1 + 1/x2 )
# Ergebnis: (x1 + x2) / (x1 * x2)
Weitere Vereinfachungen von Termen sind mit der Funktion simplify() möglich:
x = sy.S('x')
sy.simplify( sy.sin(x)**2 + sy.cos(x)**2 )
# Ergebnis: 1
sy.simplify( 3*sy.log(x) + 2 * sy.log(5*x) )
# Ergebnis: 5*log(x) + log(25)
Die Funktion simpify() kann auch genutzt werden, um die Äquivalenz zweier
Terme 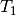 und
und 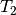 zu überprüfen. Dies ist nicht zuletzt
deshalb von Bedeutung, da die mathematische Äquivalenz in Sympy nicht mit dem
Vergleichsoperator als
zu überprüfen. Dies ist nicht zuletzt
deshalb von Bedeutung, da die mathematische Äquivalenz in Sympy nicht mit dem
Vergleichsoperator als T1 == T2 geprüft werden kann. Stattdessen kann aber
geprüft werden, ob simplify(T1 - T2) den Wert Null ergibt:
x1, x2 = sy.symbols('x1 x2')
sy.sin(x1 + x2) == sy.sin(x1) * sy.cos(x2) + sy.cos(x1) * sy.sin(x2)
# Ergebnis: False
sy.simplify(
sy.sin(x1 + x2) - ( sy.sin(x1) * sy.cos(x2) + sy.cos(x1) * sy.sin(x2) )
)
# Ergebnis: 0
Für trigonometrische Vereinfachungen kann zudem die Funktion trigsimp()
genutzt werden.
Gleichungen und Ungleichungen¶
Sympy kann insbesondere zum Lösen von Gleichungen, Gleichungssystemen und
Ungleichungen genutzt werden. Eine Gleichung kann in
Sympy folgendermaßen mittels der Funktion Equation() beziehungsweise der
Kurzform Eq() definiert werden:
x = sy.S('x')
sy.Eq(x**2 +1, 3*x -1)
# Ergebnis: x**2 + 1 == 3*x - 1
Das Ergebnis von Eq() ist ein Gleichungs-Objekt. Dieses kann wahlweise in
eine Variable gespeichert oder an die Funktion solve() übergeben werden, um
die Lösung(en) der Gleichung zu bestimmen:
sy.solve( sy.Eq(x**2 +1, 3*x -1) )
# Ergebnis: [1, 2]
Gleichungen lassen sich auch mit mehreren Parametern 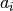 formulieren,
die bei Bedarf mittels der Funktion
formulieren,
die bei Bedarf mittels der Funktion subs() durch konkrete Werte ersetzt
werden können:
x = sy.S('x')
a, b, c = sy.symbols("a b c")
eq = sy.Eq( a*x**2 + b*x + c, 0)
# Gleichung allgemein mit x als Variable lösen:
sy.solve( eq, x )
# Ergebnis: (-b + sqrt(-4*a*c + b**2))/(2*a), -(b + sqrt(-4*a*c + b**2))/(2*a)]
# Gleichung mit Parametern a=1, b=3, c=2 lösen:
sy.solve( eq.subs( {a:1, b:-3, c:2} ) )
# Ergebnis: [1, 2]
Die Funktion solve() kann auch verwendet werden, um Gleichungssysteme zu lösen. Hierzu empfiehlt es sich, die einzelnen
Gleichungen zunächst zu einer Liste zusammenzufassen:
x1, x2, x3 = sy.symbols("x1 x2 x3")
equations = [
sy.Eq( 8*x1 + 2*x2 + 3*x3 , 15 ),
sy.Eq( 6*x1 - 1*x2 + 7*x3 , -13 ),
sy.Eq(-4*x1 + 5*x2 - 3*x3 , 21 ),
]
sy.solve(equations)
# Ergebnis: {x2: 4, x1: 2, x3: -3}
Zum Formulieren von Ungleichungen mit einer einzelnen
Variablen zu formulieren, können die folgenden Funktionen in gleicher Weise wie
die Funktion Eq() genutzt werden:
Ne() |
Ungleich | („not equal“) |
Lt() |
Kleiner als | („less than“) |
Le() |
Kleiner gleich | („less or equal“) |
Gt() |
Größer als | („greater than“) |
Ge() |
Größer gleich | („greater or equal“) |
Gegeben sei beispielsweise folgende Ungleichung:
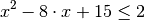
In Sympy lautet die Ungleichung etwa so:
sy.Le(x**2 - 8*x + 15, 2)
Um die Ungleichung zu lösen, wird der obige Ausdruck wiederum an die Funktion
solve() übergeben:
sy.solve( sy.Le(x**2 - 8*x + 15, 2) )
# Ergebnis: And(-sqrt(3) + 4 <= re(x), im(x) == 0, re(x) <= sqrt(3) + 4)
Man erhält also die Schnittmenge („And“) von 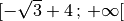 und
und ![]-\infty \,;\, \sqrt{3}+4]](../_images/math/e1059281a84d660025cf69d303215e6723cfb114.png) als Ergebnis, also das
Intervall
als Ergebnis, also das
Intervall ![[-\sqrt{3}+ 4 \,;\, +\sqrt{3}+ 4]](../_images/math/fc94aae691d8b9218d3e69741118093f7fc9fa24.png) . Die zusätzliche Angabe von
. Die zusätzliche Angabe von im(x) ==
0 bedeutet lediglich, dass es sich bei der Lösung um eine reellwertige Lösung
handelt. [1]
… to be continued …
Links
Anmerkungen:
| [1] | Eine komplexe Zahl Eine andere Möglichkeit Polynom-Ungleichungen zu lösen, bietet übrigens die
Funktion from sympy.solvers.inequalities import solve_poly_inequality
solve_poly_inequality( sy.Poly( 8*x - 13 ) , "<" )
# Ergebnis: [(-oo, 13/8)]
|

 , deren Imaginärteil
, deren Imaginärteil 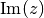 gleich Null ist, hat nur einen Realteil
gleich Null ist, hat nur einen Realteil 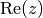 . Sie ist damit
mit einer reellen Zahl
. Sie ist damit
mit einer reellen Zahl 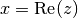 gilt.
gilt.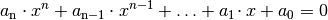 , dann kann die Ungleichung folgendermaßen gelöst werden:
, dann kann die Ungleichung folgendermaßen gelöst werden: