Zahlenrätsel (Division)

Hinweis

Das Original dieser Maxima-Beispielaufgabe kann im Original hier heruntergeladen werden. Die wxmx-Datei kann mit WxMaxima geöffnet werden.

Bei dieser Aufgabe handelt es sich um eine Knobelaufgabe bzw. um eine einfache Übungsaufgabe für lineare Gleichungssysteme.

Aufgabe:

Die Problemstellung lautet eine Zahl 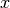zu finden, die, wenn sie durch geteilt wird, eine gegebene Zahl 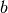ergibt ( sei ebenfalls ein bekannter, konstanter Wert). Die Aufgabe soll für und gelöst werden.

Lösung:

Es muss prinzipiell folgende Gleichung gelöst werden:

Für und lautet die Gleichung konkret:

Diese Gleichung kann bereits ohne weitere Vereinfachungen mittels Sympy gelöst werden. Der Code dazu lautet folgendermaßen:

import sympy as sy

# Sympy-Variablen initiieren:
x    = sy.S( 'x' )
a, b = sy.S( [10, 1+5/21] )

# Gleichung formulieren:
equation = sy.Eq( x/(x-a) , b )

# Gleichung lösen:
sy.solve(equation)

# Ergebnis: [52.0000000000000]

Das Ergebnis der Aufgabe lautet somit .