Quadratfläche aus Diagonale

Hinweis

Das Original dieser Maxima-Beispielaufgabe kann im Original hier heruntergeladen werden. Die wxmx-Datei kann mit WxMaxima geöffnet werden.

Bei dieser Aufgabe geht es um die Formulierung und das Lösung einer geometrischen Funktionsgleichung.

Aufgabe:

Gegeben ist die Diagonale d = 3 \cdot \sqrt{2} eines Quadrats. Wie lässt sich daraus die Fläche A des Quadrats berechnen?

Lösung:

Allgemein gilt für die Diagonale d eines Quadrats in Abhängigkeit von der Seitenlänge a:

d = \sqrt{2} \cdot a

Umgekehrt gilt somit für die Seitenlänge a in Abhängigkeit von d:

a = \frac{d}{\sqrt{2}}

Somit lässt sich aus d die Seitenlänge a und damit die Fläche A = a^2 des Quadrats berechnen. Ein Beispielcode mit Sympy kann beispielsweise so aussehen:

import sympy as sy

# Sympy-Variablen initiieren:
d = sy.S( 3 * sy.sqrt(2) )
a = sy.S( 'a' )

# Seitenlänge berechnen:
a = d / sy.sqrt(2)

# Fläche berechnen:
A = a**2

# Ergebnis: 9

Die Fläche des Quadrats beträgt somit 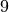9 Flächeneinheiten.