Diskriminante¶
Bei dieser Aufgabe geht es darum, die Diskriminante einer quadratischen Gleichung zu bestimmen.
Aufgabe:
Gegeben sei die quadratische Gleichung  . Wie
lautet die Diskriminante dieser Gleichung?
. Wie
lautet die Diskriminante dieser Gleichung?
Lösung:
Die Diskriminante  einer quadratischen Gleichung
einer quadratischen Gleichung  lässt sich in Abhängigkeit der Parameter
lässt sich in Abhängigkeit der Parameter  ,
,
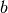 und
und  folgendermaßen bestimmen:
folgendermaßen bestimmen:

Die Aufgabe kann folgendermaßen mit Sympy gelöst werden:
import sympy as sy
# Sympy-Variable initiieren:
x = sy.S( 'x' )
# Gleichung formulieren:
f = x**2 - 8*x - 15
# Koeffizienten a, b und c bestimmen:
a = f.coeff(x, n=2)
b = f.coeff(x, n=1)
c = f.coeff(x, n=0)
D = b**2 - 4*a*c
# Ergebnis: 124
Die Diskriminante ist positiv, somit hat die Gleichung die zwei Lösungen
 :
:
x1 = ( -b + sy.sqrt(D) ) / (2 * a)
x2 = ( -b - sy.sqrt(D) ) / (2 * a)
x1.evalf()
# Ergebnis: 9.56776436283002
x2.evalf()
# Ergebnis: -1.56776436283002
Der Funktionsgraph als Ganzes kann mittels numpy und matplotlib folgendermaßen erzeugt werden:
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
# Wertereihen erzeugen:
x = np.arange(-3,11,0.01)
y = x**2 - 8*x - 15
# Funktion plotten:
plt.plot(x,y)
# Layout anpassen:
plt.axis([-3,11,-35,35])
plt.xlabel("$x$")
plt.ylabel("$y$")
plt.grid(True)
plt.text(7, 15, "$f(x)=x^2 - 8x - 15$")
plt.show()
Das Ergebnis sieht so aus:


 .
.