Quaderliste – Volumen und Oberfläche¶
Diese Aufgabe war im Original dafür vorgesehen, um in Maxima die Iteration
über Listenelemente zu demonstrieren. Bei der Verwendung von python und
sympy als Computer-Algebra-System hingegen genügt dafür bereits die
Python-Standardbibliothek.
Aufgabe:
Gegeben ist die Liste [(3,4,5), (10,8,6), (25,21,12)], deren Einträge
jeweils die Maße eines Quaders angeben (Länge, Breite und Höhe). Berechne das
Volumen sowie die Oberfläche der einzelnen Quader.
Lösung:
Das Volumen eines Quaders ist gleich dem Produkt aus Länge  , Breite
, Breite
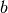 und Höhe
und Höhe  ; seine Oberfläche ist gleich der doppelten Summe
aller Flächen, die sich aus je zwei der drei Größenangaben berechnen lassen:
; seine Oberfläche ist gleich der doppelten Summe
aller Flächen, die sich aus je zwei der drei Größenangaben berechnen lassen:
![V _{\rm{Quader}} &= h \cdot b \cdot l \\[4pt]
A _{\rm{Quader}} &= 2 \cdot (h \cdot b + b \cdot l + l \cdot h)](../../_images/math/f7049da46161b53c9cf5aca7595d5c26e0575892.png)
In Python können die gesuchten Größen (auch ohne sympy) beispielsweise
durch Definition von geeigneten Funktionen berechnet werden:
# Variablen initiieren:
cuboid_dimensions = [(3,4,5), (10,8,6), (25,21,12)]
cuboid_surfaces = []
cuboid_volumes = []
# Funktionen definieren:
def get_cuboid_surface(length, width, height):
""" Calculate the surface of a cuboid."""
return 2 * (height * width + width * length + length * height)
def get_cuboid_volume(length, width, height):
""" Calculate the volume of a cuboid."""
return length * width * height
# Funktionen auf Liste anwenden:
for c in cuboid_dimensions:
cuboid_surfaces.append( get_cuboid_surface(*c) )
cuboid_volumes.append( get_cuboid_volume(*c) )
# Ergebnis:
# cuboid_surfaces: [94, 376, 2154]
# cuboid_volumes: [60, 400, 6300]
In der Hauptschleife werden beide Funktionen für die jeweiligen Größenangaben
aufgerufen; die Hilfsvariable c wird dabei, da es sich um ein um eine
Sequenz handelt, mit einem davor stehenden * an die Funktion übergeben.
Dies bewirkt, dass nicht das Zahlentripel als eigenes Objekt verwendet wird,
sondern vielmehr dessen Inhalte „ausgepackt“ und der Reihenfolge nach an die
Funktion übergeben werden.
