Lösungen zur Optik¶
Ausbreitung des Lichts¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Ausbreitung des Lichts.
Licht breitet sich von der Sonne geradlinig in alle Richtungen unseres Sonnensystems aus. Nur der schmale Lichtkegel, der dabei auf die Erde trifft, wird von uns direkt wahrgenommen. Zusätzlich können wir das Sonnenlicht wahrnehmen, wenn es auf andere Himmelskörper (vor allem Planeten und Kometen) trifft.
Da das übrige Sonnenlicht unser Auge nicht erreicht, erscheint uns das restliche Weltall als dunkel.
Die Zeit, die Licht zum Durchqueren eines Zimmers benötigt, beträgt weniger als
![\unit[\frac{1}{10\,000\,000}]{s}](../_images/math/473d8ca16a2bac6965eac7dbc3dd3ccae635cc6d.png) . Zwar wird Licht beim Durchqueren von
verschiedenen „optisch dichten“ Stoffen (beispielsweise Wasser) etwas abgebremst, doch
ist es stets so schnell, dass es für eine konstante Beleuchtung ständig
von einer Lichtquelle neu erzeugt werden muss.
. Zwar wird Licht beim Durchqueren von
verschiedenen „optisch dichten“ Stoffen (beispielsweise Wasser) etwas abgebremst, doch
ist es stets so schnell, dass es für eine konstante Beleuchtung ständig
von einer Lichtquelle neu erzeugt werden muss.Das „Einfangen“ von winzigen Lichtmengen in einem lichtundurchlässigen Behältnis ist zwar möglich, doch können wir es dann nicht sehen – dafür müsste das Licht ja aus dem Behältnis entweichen und in unsere Augen gelangen..
Reflexion von Licht¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Reflexion von Licht.
Nur diejenigen Stoffe, die eine glatte Oberfläche besitzen, können Licht direkt reflektieren – beispielsweise Diamant, Fensterglas, Flüssigkeiten, Metalle und Kunststoffe (geschliffen und poliert), Salz, Zucker, Wasser, Schnee und Eis, Hochglanzpapier, etc.
Stoffe mit rauhen Oberflächen können Licht diffus, d.h. in alle Richtungen streuend, reflektieren. Das reflektierte Licht erscheint dann als „matt“, d.h. es treten keine Glanzstellen auf.
Das Licht, das von Sternen zur Erde gelangt, trifft auf seinem Weg durch das Weltall auf kein Hindernis; es breitet sich daher geradlinig und „verlustfrei“ über beliebig lange Strecken aus. Nachts können wir, wenn der Himmel nicht zu bewölkt oder neblig ist, dieses Licht daher auch auf der Erde beobachten. Die besten Beobachtungen können allerdings von Satelliten aus gemacht werden, denn entlang des Weges durch die Atmosphäre trifft einfallende Licht auf kleine Wasser-Tröpfchen und wird von diesen aus gleichmäßig in alle Richtungen reflektiert („gestreut“). Diese Streuung findet vor allem in den erdnahen Atmosphären-Schichten statt, da dort eine höhere Gas- und Feuchtigkeitsdichte vorherrscht.
Aus dem gleichen Grund können wir auch Lichtquellen auf der Erde nur bedingt weit sehen; bei nebligem Wetter wird die Sichtweite nochmals erheblich verkürzt.
Lichtbrechung¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Lichtbrechung.
Die Lichtgeschwindigkeit
 in dem optischen Medium lässt sich
berechnen, indem man die Lichtgeschwindigkeit
in dem optischen Medium lässt sich
berechnen, indem man die Lichtgeschwindigkeit ![c_0 = \unit[3,0 \cdot
10^8]{m/s}](../_images/math/7db920d24bc55ed28e70638edf366bbac05bee47.png) im Vakuum durch die Brechzahl
im Vakuum durch die Brechzahl 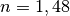 des optischen Mediums
teilt:
des optischen Mediums
teilt:![c = \frac{c_0}{n} = \frac{\unit[3,0 \cdot 10^8]{m/s}}{1,48} \approx
\unit[2,03 \cdot 10^8]{m/s}](../_images/math/ab10b0268c6e0da488e3268da34341bc9e177a7e.png)
Die Lichtgeschwindigkeit in dem optischen Medium beträgt somit rund
![\unit[2,03 \cdot 10^8]{m/s}](../_images/math/0603b4ce41a3ea04caf74edbfd63b0dc6e6b2d94.png) .
.
Die (absolute) Brechzahl
 des optischen Mediums lässt sich mittels
der angegebenen Lichtgeschwindigkeit
des optischen Mediums lässt sich mittels
der angegebenen Lichtgeschwindigkeit ![c=\unit[2,29 \cdot 10^8]{m/s}](../_images/math/a95efea9e542f1e228fa838d7dafcfffce2b8bbe.png) berechnen, indem das Verhältnis aus der Lichtgeschwindigkeit im Vakuum und
der Lichtgeschwindigkeit im Medium gebildet wird:
berechnen, indem das Verhältnis aus der Lichtgeschwindigkeit im Vakuum und
der Lichtgeschwindigkeit im Medium gebildet wird:![n = \frac{c_0}{c} = \frac{\unit[3,0 \cdot 10^8]{m/s}}{\unit[2,29 \cdot
10^8]{m/s}} = 1,31](../_images/math/afc02751cd0ca02e649a873fb07ac42c3a97769c.png)
Die Brechzahl des optischen Mediums beträgt somit
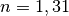 . (Ein
Vergleich mit tabellarischen Werten lässt vermuten, dass es sich bei dem
Medium um Eis handelt.)
. (Ein
Vergleich mit tabellarischen Werten lässt vermuten, dass es sich bei dem
Medium um Eis handelt.)
Trifft ein Lichtstrahl von einem optisch dünnen Medium (Luft,
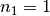 )
auf ein optisch dichteres Medium (beispielsweise Glycerin,
)
auf ein optisch dichteres Medium (beispielsweise Glycerin, 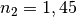 ), so wird er zur Senkrechten hin gebrochen. Als Zusammenhang zwischen
den Winkeln des einfallenden und gebrochenen Strahls gilt folgende Formel:
), so wird er zur Senkrechten hin gebrochen. Als Zusammenhang zwischen
den Winkeln des einfallenden und gebrochenen Strahls gilt folgende Formel: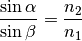
Im gegebenen Fall ist
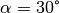 und
und 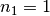 , gesucht ist
der Winkel
, gesucht ist
der Winkel 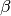 . Löst man die Formel nach der gesuchten Größe auf, so
folgt:
. Löst man die Formel nach der gesuchten Größe auf, so
folgt: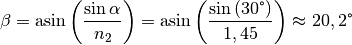
Der Winkel des gebrochenen Strahls beträgt etwa
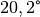 .
.
Die relative Brechzahl
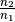 für den Übergang eines
Lichtsrahls von Medium 1 (Quarzglas,
für den Übergang eines
Lichtsrahls von Medium 1 (Quarzglas, 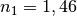 ) in Medium 2
(Flintglas,
) in Medium 2
(Flintglas, 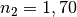 ) lässt sich als Quotient der Brechzahlen
beider Medien berechnen:
) lässt sich als Quotient der Brechzahlen
beider Medien berechnen: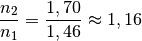
Die Lichtbrechung erfolgt so, als würde ein sich zunächst in Luft ausbreitender Lichtstrahl auf ein optisches Medium mit einer Brechzahl von
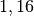 treffen: Der Lichtstrahl wird zur Senkrechten hin gebrochen,
der Sinus des Brechungswinkels
treffen: Der Lichtstrahl wird zur Senkrechten hin gebrochen,
der Sinus des Brechungswinkels 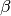 ist um das
ist um das 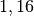 -fache
kleiner als der Sinus des Einfallswinkels
-fache
kleiner als der Sinus des Einfallswinkels  .
.Ist der Einfallswinkel
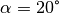 , so beträgt der
Brechungswinkel
, so beträgt der
Brechungswinkel 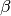 folglich:
folglich:![\sin{\beta} &= \frac{\sin{(\alpha)} \cdot n_1}{n_2} \quad \Leftrightarrow
\quad \beta = \text{asin}\left( \frac{\sin{(\alpha)} \cdot n_1}{n_2}
\right) \\[4pt]
\beta &= \text{asin}\left( \frac{\sin{(20 \degree)}}{1,16}\right) \approx
17\degree](../_images/math/b1db16b1497060abb411613e14a28a71758ae38f.png)
Der Winkel
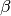 des gebrochenen Lichtstrahls beträgt somit rund
des gebrochenen Lichtstrahls beträgt somit rund
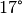 .
.
Da der im Winkel
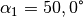 einfallende Lichtstrahl an der
Grenzfläche zur Senkrechten hin gebrochen wird (
einfallende Lichtstrahl an der
Grenzfläche zur Senkrechten hin gebrochen wird (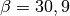 ), muss
für die Brechzahlen beider Medien
), muss
für die Brechzahlen beider Medien 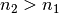 gelten. Mit
gelten. Mit 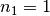 folgt aus dem Brechungsgesetz:
folgt aus dem Brechungsgesetz: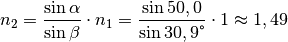
Beim zweiten Übergang
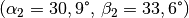 wird der Lichtstrahl von der Senkrechten weg gebrochen, folglich
muss
wird der Lichtstrahl von der Senkrechten weg gebrochen, folglich
muss 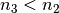 gelten. Mit
gelten. Mit 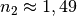 folgt:
folgt: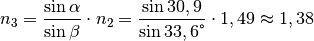
Die Brechzahlen betragen somit näherungsweise
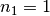 (Luft),
(Luft),
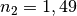 (beispielsweise Plexiglas oder Leinöl) und
(beispielsweise Plexiglas oder Leinöl) und 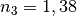 (beispielsweise Wasser mit 1 mol/l Saccharose).
(beispielsweise Wasser mit 1 mol/l Saccharose).
Geht ein Lichtstrahl von Diamant
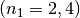 in Luft
in Luft 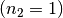 über, so gilt für den Grenzwinkel
über, so gilt für den Grenzwinkel 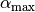 :
:![\sin{\alpha_{\mathrm{max}}} &= \frac{n_2}{n_1} \quad \Leftrightarrow \quad
\alpha_{\mathrm{max}} = \text{asin}\left( \frac{n_2}{n_1}\right) \\[4pt]
\alpha_{\mathrm{max}} &= \text{asin}\left( \frac{1}{2,4}\right) \approx
24,6\degree](../_images/math/0a3de13dca1edd8c2a517fe38801807b113fe550.png)
Der Grenzwinkel
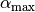 beim Übergang eines Lichtstrahls
von Diamant in Luft beträgt somit rund
beim Übergang eines Lichtstrahls
von Diamant in Luft beträgt somit rund 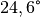 . Trifft ein Lichstrahl
mit einem größeren Winkel auf die Grenzfläche, so tritt Totalreflexion ein.
Der Lichtstrahl kann den Diamanten (an dieser Stelle) also nicht mehr
verlassen, sondern wird anstelle dessen gemäß des Reflexionsgesetzes in den
Diamanten zurück reflektiert.
. Trifft ein Lichstrahl
mit einem größeren Winkel auf die Grenzfläche, so tritt Totalreflexion ein.
Der Lichtstrahl kann den Diamanten (an dieser Stelle) also nicht mehr
verlassen, sondern wird anstelle dessen gemäß des Reflexionsgesetzes in den
Diamanten zurück reflektiert.
Die zwei möglichen Fälle, in denen Licht beim Übergang von einem transparenten Medium in ein anderes nicht gebrochen wird, lassen sich gut erkennen, indem man die Gleichung für das Brechungsgesetz folgendermaßen umstellt:
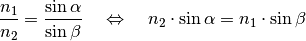
Soll keine Lichtbrechung stattfinden, so muss
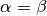 gelten.
Dies ist einerseits der Fall, wenn
gelten.
Dies ist einerseits der Fall, wenn 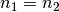 gilt, also die
Brechungsindizes der beiden Medien gleich sind. Andererseits gilt auch
gilt, also die
Brechungsindizes der beiden Medien gleich sind. Andererseits gilt auch
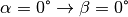 und damit
und damit
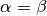 , wenn der eintretende Lichtstrahl senkrecht zur
Oberfläche der Grenzschicht verläuft. In allen anderen Fällen tritt
Lichtbrechung auf.
, wenn der eintretende Lichtstrahl senkrecht zur
Oberfläche der Grenzschicht verläuft. In allen anderen Fällen tritt
Lichtbrechung auf.
Linsensysteme¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Linsensysteme.
Die Brechkraft
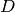 einer Sammellinse mit einer Brennweite von
einer Sammellinse mit einer Brennweite von ![f =
\unit[150]{mm} = \unit[0,150]{m}](../_images/math/8d6a3e3bdaf2b97d8dd5d55218f6ef4b07356421.png) beträgt:
beträgt:![D = \frac{1}{f} = \frac{1}{\unit[0,150]{m}} = \unit[6,67]{dpt}](../_images/math/a0a7b372e5ee38c5b588a024397b2b208250f4d4.png)
Die Linse hat also eine Brechkraft von rund
.
Die Brennweite
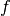 einer Zerstreuungslinse mit einer Brechkraft von
einer Zerstreuungslinse mit einer Brechkraft von
![D = \unit[-4,0]{dpt}](../_images/math/9006416c7cc88e71f5b234a5ab26fa54db4b6c0d.png) lässt sich folgendermaßen berechnen:
lässt sich folgendermaßen berechnen:
![D = \frac{1}{f} = \frac{1}{\unit[-4]{dpt}} =
\frac{1}{\unit[-4]{\frac{1}{m}}} = \unit[-0,25]{m}](../_images/math/8bcc5d8e0503520654b71266783a31ad9c4535a5.png)
Die Brennweite der Zerstreuungslinse beträgt also rund
![\unit[-25]{cm}](../_images/math/4d0baa6a1b5843c77fd285114587778fece27c9f.png) .
.
Die Brennweite
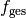 des Linsensystems erhält man, indem
man die Kehrwerte der Brennweiten beider Linsen addiert und anschließend den
Kehrwert von diesem Ergebnis bildet. Mit
des Linsensystems erhält man, indem
man die Kehrwerte der Brennweiten beider Linsen addiert und anschließend den
Kehrwert von diesem Ergebnis bildet. Mit ![f_1 = \unit[50]{mm} =
\unit[0,050]{m}](../_images/math/18475470ee2607accce2c3954e6c52ad5ca53fb7.png) und
und ![f_2 = \unit[75]{mm}= \unit[0,075]{m}](../_images/math/f59faeccf72f1c3f3c4a70ebbd7ebadd76f3d448.png) folgt:
folgt: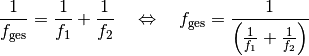
![f_{\mathrm{ges}} = \frac{1}{\frac{1}{\unit[0,050]{m}} +
\frac{1}{\unit[0,075]{m}}} = \unit[0,03]{m}](../_images/math/8fb1687ddd0719a63891c8196ab8143353b3498d.png)
Die Brennweite des Linsensystems beträgt somit insgesamt
![\unit[30]{mm}](../_images/math/ed045d3767f16721558107d186562ea273689b43.png) . Das gleiche Ergebnis kann man erhalten, indem man
zunächst beide Brennweiten mittels der Formel
. Das gleiche Ergebnis kann man erhalten, indem man
zunächst beide Brennweiten mittels der Formel 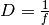 in
Dioptrien umrechnet, die Dioptrienzahlen addiert, und von der
Gesamt-Dioptrienzahl wiederum auf die zugehörige Brennweite umrechnet:
in
Dioptrien umrechnet, die Dioptrienzahlen addiert, und von der
Gesamt-Dioptrienzahl wiederum auf die zugehörige Brennweite umrechnet:![D_1 &= \frac{1}{f_1} = \frac{1}{\unit[0,050]{m}} = \unit[20,0]{dpt} \\
D_2 &= \frac{1}{f_2} = \frac{1}{\unit[0,075]{m}} = \unit[13,3]{dpt} \\
D_{\mathrm{ges}} &= D_1 + D_2 = \unit[20,0]{dpt} + \unit[13,3]{dpt} =
\unit[33,3]{dpt} \\
f_{\mathrm{ges}} &= \frac{1}{D_{\mathrm{ges}}} =
\frac{1}{\unit[33,3]{dpt}} = \frac{1}{\unit[33,3]{\frac{1}{m}}} =
\unit[0,03]{m}](../_images/math/67947742245329c02deedca662cd2d5061e61cf8.png)
Auch mit diesem Rechenweg erhält man eine Gesamt-Brennweite von
![\unit[30]{mm}](../_images/math/ed045d3767f16721558107d186562ea273689b43.png) .
.
Um die Entfernung
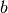 des Bildes von der Linse zu berechnen, muss man
die gegebenen Größen
des Bildes von der Linse zu berechnen, muss man
die gegebenen Größen ![D = \frac{1}{f} = \unit[5,0]{dpt} =
\frac{5,0}{\unit{\frac{1}{m}}}](../_images/math/d86e448511a509ed193d6c16d7f694a2e99a2dce.png) und
und ![g = \unit[60]{cm} = \unit[0,6]{m}](../_images/math/2e86cadccf881abad2fadd68369343baadf2eedf.png) in die Linsengleichung einsetzen:
in die Linsengleichung einsetzen: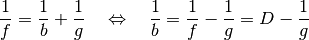
![b = \frac{1}{D - \frac{1}{g}} = \frac{1}{\unit[5]{\frac{1}{m}} -
\frac{1}{\unit[0,6]{m}}} = \frac{1}{\unit[3,33]{\frac{1}{m}}} =
\unit[0,3]{m}](../_images/math/731fa2b8fa1c0535f485f750a63872a0c4274235.png)
Das Bild befindet sich also im Abstand von
![\unit[30]{cm}](../_images/math/9a0de1927088ad2e327a09827f41a8916d697d0e.png) hinter der
Linse. Für den Abbildungsmaßstab
hinter der
Linse. Für den Abbildungsmaßstab 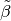 folgt somit:
folgt somit:![\tilde{\beta} = \frac{b}{g} = \frac{\unit[0,3]{m}}{\unit[0,6]{m}} =
\frac{1}{2}](../_images/math/816269c27d22aedd3dc18e2d7b04bdd654adae4a.png)
Der Gegenstand wird durch die Linse somit um die Hälfte verkleinert abgebildet.
Wenn die Brechkraft einer Zerstreuungslinse
![D = \unit[-8,0]{dpt}](../_images/math/59e6fed41559dbcb0c0ec9d8a84b976260a3e80f.png) beträgt, so entspricht dies einer Brennweite von
beträgt, so entspricht dies einer Brennweite von ![f = \frac{1}{D} =
\frac{1}{\unit[-8]{dpt}} = \unit[0,125]{m}](../_images/math/46729258f349b23908dcf7eb27a2ef3358e08199.png) . Setzt man diese Größe sowie die
Entfernung
. Setzt man diese Größe sowie die
Entfernung ![g=\unit[9,0]{cm} = \unit[0,090]{m}](../_images/math/9cae8b4c9234286284653a2f047bbdaa3a2c361f.png) des Gegenstands von der
Linse in die Linsengleichung ein, so erhält man:
des Gegenstands von der
Linse in die Linsengleichung ein, so erhält man: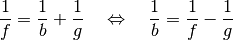
![b = \frac{1}{\left(\frac{1}{f} - \frac{1}{g}\right)} = \frac{1}{\left(
\frac{1}{\unit[-0,125]{m}} - \frac{1}{\unit[0,090]{m}}\right)} =
\unit[-0,052]{m}](../_images/math/8942e718b311cae34b90f4864ffb27b37ca6fda3.png)
Das Bild des Gegenstands befindet sich somit in einem Abstand von
![\unit[5,2]{cm}](../_images/math/02e5e24be0480a2ebecec6179e39aa9cb919d109.png) vor (!) der Zerstreuungslinse.
vor (!) der Zerstreuungslinse.
Optische Geräte¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Optische Geräte.
Die Vergrößerung
 des Kepler-Fernrohrs entspricht dem Verhältnis der
Brennweiten
des Kepler-Fernrohrs entspricht dem Verhältnis der
Brennweiten ![f_{\mathrm{Obj}} = \unit[0,32]{m}](../_images/math/72cb4b31079045d407b47728ea8ac02ad4c79cc8.png) des Objektivs und
des Objektivs und
![f_{\mathrm{Ok}} = \unit[0,04]{m}](../_images/math/079b02dcbe48d49f8f54cd068477d3323fc87bea.png) des Okulars:
des Okulars:![V = \frac{f_{\mathrm{Obj}}}{f_{\mathrm{Ok}}} =
\frac{\unit[0,32]{m}}{\unit[0,04]{m}} = 8](../_images/math/1a89e0c69e09f58b34b51d136ed1c4c20f513527.png)
Das Kepler-Fernrohr hat somit eine
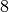 -fache Vergrößerung.
-fache Vergrößerung.
