Linsensysteme¶
Häufig wird in optischen Geräten nicht nur eine einzelne, sondern vielmehr eine Kombination mehrerer Sammel- beziehungsweise Zerstreuungslinsen genutzt. Einige wichtige Eigenschaften, die sich bei derartigen Anordnungen auftreten, werden im folgenden Abschnitt näher beschrieben.
Brennweite und Brechkraft eines Linsensystems¶
Soll die Brennweite 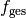 eines solchen Systems mehrerer Linsen
bestimmt werden, so kann man die Kehrwerte der Brennweiten aller Linsen
addieren, um den Kehrwert der Gesamtbrennweite zu erhalten:
eines solchen Systems mehrerer Linsen
bestimmt werden, so kann man die Kehrwerte der Brennweiten aller Linsen
addieren, um den Kehrwert der Gesamtbrennweite zu erhalten:
(1)¶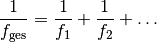
Die Brennweiten von Sammellinsen werden dabei positiv, die von Zerstreuungslinsen negativ gezählt.
Beispiele:
Eine Kombination zweier Sammellinsen mit den Brennweiten
![f_1 =
\unit[10]{cm}](../_images/math/0c5eb49903dcf6ceea3eaeeaae946a8caaa8950c.png) und
und ![f_2 = \unit[15]{cm}](../_images/math/883ae29ec191c68c815f62e219688cf4d075a342.png) hat insgesamt folgende
Brennweite:
hat insgesamt folgende
Brennweite:![\frac{1}{f_{\mathrm{ges}}} = \frac{1}{\unit[0,1]{m}} +
\frac{1}{\unit[0,15]{m}} \quad \Leftrightarrow \quad f_{\mathrm{ges}} =
\frac{1}{\frac{1}{\unit[0,1]{m}} + \frac{1}{\unit[0,15]{m}}} =
\unit[0,06]{m}](../_images/math/567fd9a192c5fea4914610c8ed66bfb09b381c82.png)
Die beiden Linsen haben zusammen somit die gleiche Brechkraft wie eine einzelne (Sammel-)Linse mit
![f = \unit[6]{cm}](../_images/math/57bab1c1b2b649f6b5276cd76e2d1e99c639d93b.png) Brennweite.
Brennweite.Eine Kombination einer Sammellinse mit einer Brennweite von
![f_1 =
\unit[30]{cm}](../_images/math/bc319a3dbbcb52dd6063e4898a5827860dbfa920.png) und einer Zerstreuungslinse mit einer Brennweite von
und einer Zerstreuungslinse mit einer Brennweite von
![f_2 = \unit[-10]{cm}](../_images/math/195cfb517e060da54271b1d11ce29b9d66260c21.png) hat insgesamt folgende Brennweite:
hat insgesamt folgende Brennweite:![\frac{1}{f_{\mathrm{ges}}} = \frac{1}{\unit[0,3]{m}} -
\frac{1}{\unit[0,1]{m}} \quad \Leftrightarrow \quad f_{\mathrm{ges}} =
\frac{1}{\frac{1}{\unit[0,3]{m}} - \frac{1}{\unit[0,1]{m}}} =
-\unit[0,15]{m}](../_images/math/3e9cfe85ba02d20c48c951b398461eaa2d6a91ac.png)
Die beiden Linsen haben zusammen somit die gleiche Brechkraft wie eine einzelne (Zerstreuungs-)Linse mit
![f = -\unit[15]{cm}](../_images/math/c59f811d7ae61ae46023ec65d5556e84f0236ac8.png) Brennweite.
Brennweite.
Kombiniert man eine Sammellinse mit einer Zerstreuungslinse (betragsweise)
gleicher Brennweite, so ergibt sich 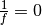 beziehungsweise
beziehungsweise
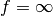 . Ein solches System hat eine unendliche Brennweite, d.h.
einfallende Lichtstrahlen werden durch diese Linsenkombination quasi nicht
gebrochen, sondern durchlaufen es ohne Ablenkung.
. Ein solches System hat eine unendliche Brennweite, d.h.
einfallende Lichtstrahlen werden durch diese Linsenkombination quasi nicht
gebrochen, sondern durchlaufen es ohne Ablenkung.
Die Brennweiten von Linsen lassen sich, wie im letzten Abschnitt gezeigt, nicht
direkt addieren, sondern nur ihre Brennwerte. Aus diesem Grund wurde als
physikalische Größe die so genannte Brechkraft 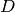 eingeführt, die als
Kehrwert der Brennweite
eingeführt, die als
Kehrwert der Brennweite 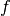 definiert ist:
definiert ist:
(2)¶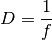
Die Brechkraft einer Linse wird in Dioptrien ![(\unit[]{dpt})](../_images/math/3898071d2403311b5060f390c8eecb03093ed661.png) angegeben.
Eine Dioptrie entspricht der Brechkraft einer Sammellinse, die eine Brennweite
von einem Meter hat:
angegeben.
Eine Dioptrie entspricht der Brechkraft einer Sammellinse, die eine Brennweite
von einem Meter hat:
![\unit[1]{dpt} = \unit[1]{\frac{1}{m}}](../_images/math/ac5d80ecaeffd4b0088556a82509e4135d54f7ac.png)
Je kleiner die Brennweite einer Linse ist, desto größer ist ihre Brechkraft
und somit auch ihre Dioptrienzahl; beispielsweise entspricht eine Brennweite von
![\unit[\frac{1}{2}]{m}](../_images/math/3ecb8c99967e79d27145a30276470c513cc0a333.png) einer Brechkraft von
einer Brechkraft von ![\unit[2]{dpt}](../_images/math/8eca0fbbd4f8127604e2bbb81ab375cdfb5b98c2.png) oder
eine Brennweite von
oder
eine Brennweite von ![\unit[\frac{1}{4}]{m}](../_images/math/6d0f46cd2ed448f36ba111ce3a13579bd91098cd.png) einer Brechkraft von
einer Brechkraft von
![\unit[4]{dpt}](../_images/math/045b75198d98f71414412bb61b3f94622d93ef0e.png) .
.
Die Dioptrienzahl 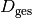 eines Linsensystems ist gleich der
Summe der Dioptrienzahlen der einzelnen Linsen; die Brechkraft von Sammellinsen
erhält dabei wiederum ein positives, die von Zerstreuungslinsen ein negatives
Vorzeichen. Es gilt also:
eines Linsensystems ist gleich der
Summe der Dioptrienzahlen der einzelnen Linsen; die Brechkraft von Sammellinsen
erhält dabei wiederum ein positives, die von Zerstreuungslinsen ein negatives
Vorzeichen. Es gilt also:
(3)¶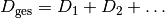
Linsenfehler und Abhilfen¶
Die Brechkraft einer Sammel- beziehungsweise Zerstreuungslinse wird üblicherweise für Lichtstrahlen angegeben, die nahe der optischen Achse auf die Linse treffen. Strahlen, die auf den Randbereich der Linse treffen („Randstrahlen“), werden stärker gebrochen. Einfallende Parallelstrahlen durchlaufen also keine gemeinsamen Brennpunkt und können somit durch die Linse nicht gemeinsam mit den achsennah einfallenden Strahlen in einem einzigen Punkt scharf abgebildet werden. Es gilt:
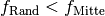
Die Verschiebung des Brennpunkts bei Randstrahlen wird als sphärische Aberration bezeichnet. Um diesen Linsenfehler zu verhindern, gibt es grundsätzlich zwei Möglichkeiten:
- Durch eine Blende kann verhindert werden, dass Lichtstrahlen auf den Rand der Linse treffen. Hierdurch werden jedoch der Bildausschnitt und die einfallende Lichtstärke reduziert.
- Durch eine Kombination einer Sammel- und einer Zerstreuungslinse mit unterschiedlichen Brechkräften kann gemäß Gleichung (1) ein Linsensystem mit der gewünschten Brechkraft erzeugt werden, das zugleich die sphärische Aberration (nahezu) auf Null reduziert. Derartige Linsensysteme werden beispielsweise in Objektiven von Fotokameras eingesetzt.
Ein weiterer Linsenfehler entsteht dadurch, dass verschieden farbiges Licht beim Durchgang durch die Linse ungleich stark gebrochen wird; in der Regel wird rotes Licht am schwächsten, violettes Licht am stärksten gebrochen. Dieser Effekt wird als chromatische Aberration bezeichnet. Es gilt:
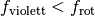
Im Gegensatz zur sphärischen chromatische Aberration kann die chromatische Aberration nie vollständig durch geschickte Linsen-Kombinationen beseitigt werden.
Der Abbildungsmaßstab und die Linsengleichung¶
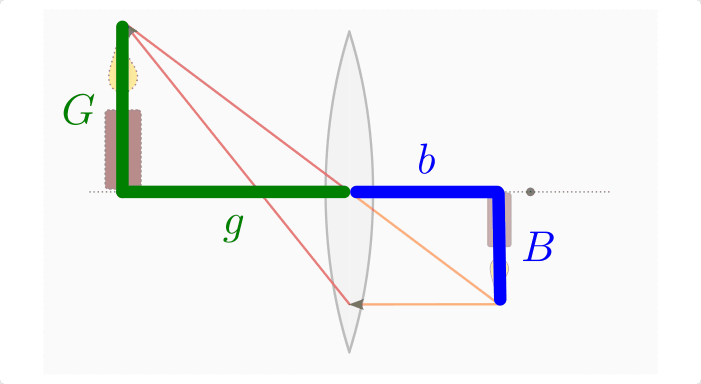
Das vergrößerte beziehungsweise verkleinerte Bild, das sich bei einer Abbildung durch eine optische Linse ergibt, kann nicht nur durch geometrische Konstruktion sondern auch rechnerisch bestimmt werden.
Wendet man den 2. Strahlensatz auf die obige
Abbildung an, so erkennt man, dass die Größe 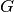 des Gegenstands im
gleichen Verhältnis zur Entfernung
des Gegenstands im
gleichen Verhältnis zur Entfernung 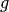 des Gegenstands von der Linse steht
wie die Größe des Bildes
des Gegenstands von der Linse steht
wie die Größe des Bildes 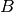 zu seiner Entfernung
zu seiner Entfernung 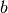 von der Linse:
von der Linse:
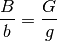
Formt man diese für Sammel- wie für Zerstreuungslinsen gleichermaßen gültige
Gleichung um, so erhält man den Maßstab 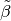 , der sich bei der
Abbildung durch die Linse ergibt:
, der sich bei der
Abbildung durch die Linse ergibt:
(4)¶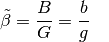
Der Abbildungsmaßstab 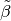 hat keine Einheit, sondern ist ein
reines Zahlenverhältnis. Sein Wert ist kleiner als Eins im Fall einer
Verkleinerung und größer als Eins im Fall einer Vergrößerung.
hat keine Einheit, sondern ist ein
reines Zahlenverhältnis. Sein Wert ist kleiner als Eins im Fall einer
Verkleinerung und größer als Eins im Fall einer Vergrößerung.
Häufig lassen sich im praktischen Anwendungsfall die Gegenstandsgröße 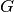 sowie die Gegenstandsweite
sowie die Gegenstandsweite 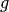 durch eine gewöhnliche Längenmessung
ermitteln. Um damit jedoch mittels Gleichung (4) auf die
Bildgröße
durch eine gewöhnliche Längenmessung
ermitteln. Um damit jedoch mittels Gleichung (4) auf die
Bildgröße 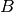 und die Bildweite
und die Bildweite 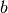 schließen zu können, ist neben
der eine zusätzliche Gleichung nötig.
schließen zu können, ist neben
der eine zusätzliche Gleichung nötig.
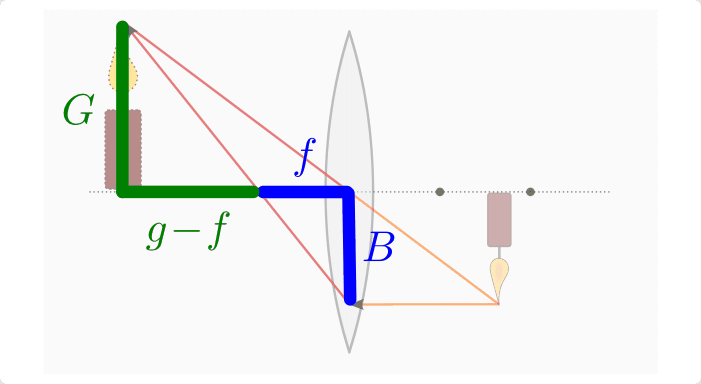
Wendet man den 2. Strahlensatz auf die obige
Abbildung an, so erkennt man, dass die Größe 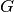 des Gegenstands im
gleichen Verhältnis zur Größe
des Gegenstands im
gleichen Verhältnis zur Größe 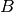 des Bildes steht wie die Entfernung
des Bildes steht wie die Entfernung
 des Gegenstands vom Brennpunkt zur Brennweite
des Gegenstands vom Brennpunkt zur Brennweite 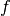 der Linse:
der Linse:
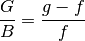
Die rechte Seite dieser Gleichung kann in zwei Terme aufgeteilt werden:
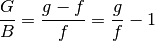
Das Verhältnis 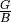 der Gegenstands- zur Bildgröße ist nach
Gleichung (4) mit dem Verhältnis
der Gegenstands- zur Bildgröße ist nach
Gleichung (4) mit dem Verhältnis 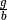 der Gegenstands- zur Bildweite identisch. Somit gilt:
der Gegenstands- zur Bildweite identisch. Somit gilt:
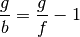
Dividiert man diese Gleichung durch 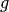 und sortiert die Terme, so erhält
man die so genannte „Linsengleichung“, die üblicherweise in folgender Form
angegeben wird:
und sortiert die Terme, so erhält
man die so genannte „Linsengleichung“, die üblicherweise in folgender Form
angegeben wird:
(5)¶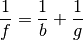
Bei einer bekannten Brennweite kann mittels dieser Gleichung anhand der
Gegenstandsweite 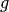 unmittelbar die Bildweite
unmittelbar die Bildweite 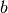 berechnet werden.
Setzt man den erhaltenen Wert von
berechnet werden.
Setzt man den erhaltenen Wert von 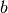 in die Abbildungsgleichung
(4) ein, so erhält man schließlich auch die gesuchte
Bildgröße
in die Abbildungsgleichung
(4) ein, so erhält man schließlich auch die gesuchte
Bildgröße 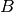 und damit den Abbildungsmaßstab.
und damit den Abbildungsmaßstab.
Hinweis
Zu diesem Abschnitt gibt es Übungsaufgaben.