Mechanische Wellen¶
Bestehen Wechselwirkungen zwischen einzelnen schwingenden Objekten, so kann sich der Schwingungszustand eines Oszillators jeweils auf die benachbarten Oszillatoren ausbreiten. Eine solche räumliche Ausbreitung eines Schwingungszustands infolge von Kopplungseffekten bezeichnet man als (mechanische) Welle. Durch Wellen wird also ausschließlich Energie, jedoch keine Materie übertragen.
Beispiele:
- Seilwellen entstehen, wenn ein Seil periodisch in Querrichtung hin- und herbewegt wird.
- Schallwellen entstehen durch schnelle Schwingungen eines elastischen Körpers, beispielsweise einer Lautsprechermembran oder einer Stimmgabel.
- Wasserwellen entstehen meist dadurch, dass Wind über die ansonsten glatte Wasseroberfläche streift. Die Wasseroberfläche hebt und senkt sich dadurch in periodischen Abständen.
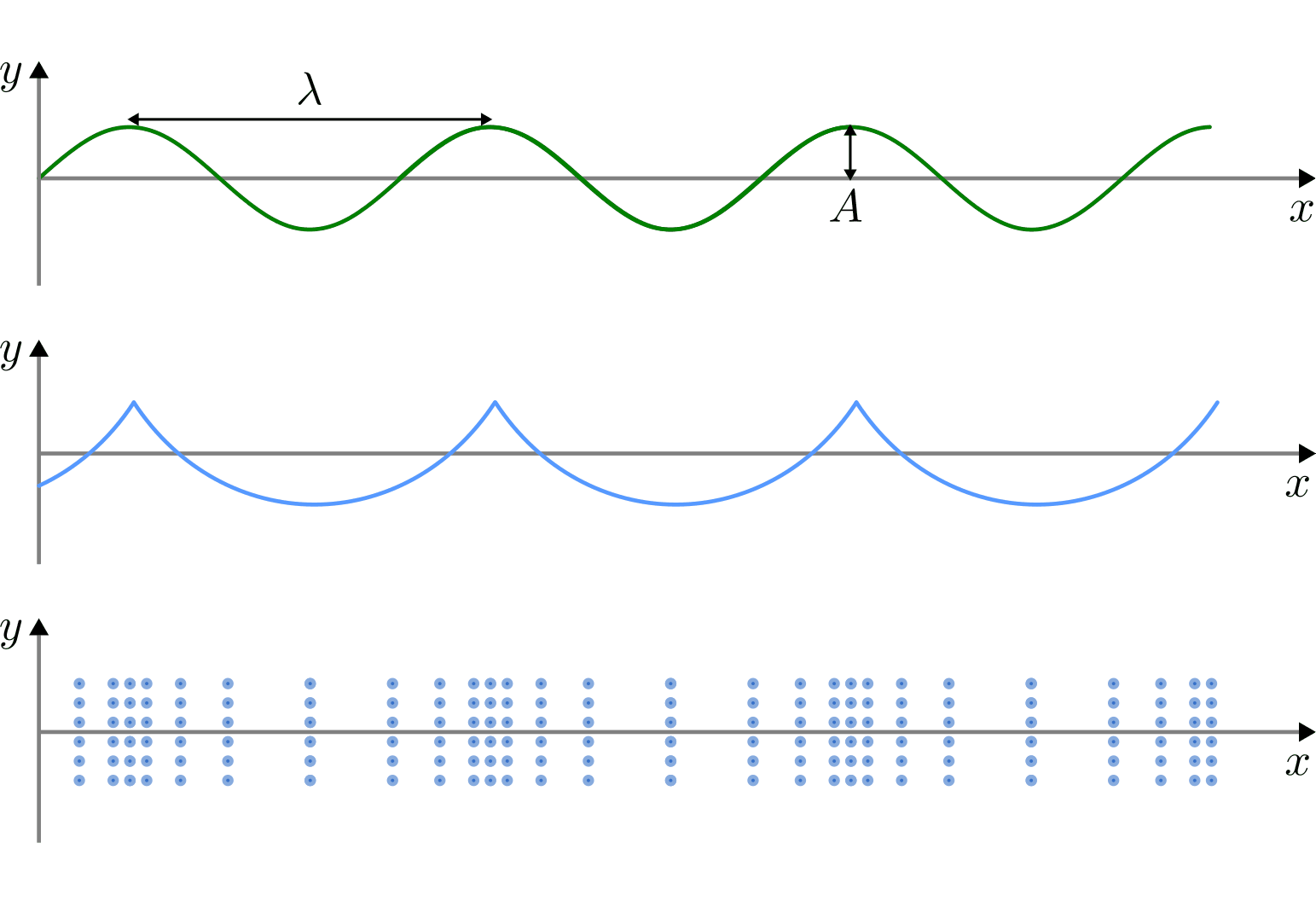
In Diagrammen wird bei Wellen – anders als Schwingungen – meistens nicht der zeitliche, sondern der räumliche Verlauf dargestellt. Fällt ein Stein ins Wasser, so entstehen um die Eintauchstelle kreisförmige Wellen, die sich nach allen Seiten ausbreiten. Von oben betrachtet ergeben sich sich in diesem Fall konzentrische Kreise mit zunehmendem Radius; in der Seitenansicht haben die Wellen näherungsweise einen räumlich periodischen Verlauf. Ist die Wellenform sinusförmig (beispielsweise bei Seilwellen), so nennt man die Welle harmonisch, andernfalls nennt man sie anharmonisch (beispielsweise Wasserwellen).
Längswellen und Querwellen
Allgemein werden Wellen in so genannte Längs- und Querwellen unterteilt:
- Bei Längswellen verlaufen die Schwingungen parallel zur Ausbreitungsrichtung der Welle. Dies ist beispielsweise bei Druck- oder Schallwellen in Luft der Fall.
- Bei Querwellen verlaufen die Schwingungen senkrecht zur Ausbreitungsrichtung der Welle. Dies ist beispielsweise bei Seilwellen oder Schwingungen von Instrumentensaiten sowie bei elektromagnetischen Wellen bzw. Lichtwellen der Fall.
Längswellen sind grundsätzlich mit einer Ausbreitung von Verdünnungen und Verdichtungen des Trägermediums verbunden, so dass sie sich nur in komprimierbaren Materialien ausbreiten können. In manchen Fällen, beispielsweise bei Erdbebenwellen oder bei Schallwellen in Flüssigkeiten und Festkörpern, treten Längs- und Querwellen gleichzeitig auf.
Ausbreitung von Wellen¶
Zur physikalischen Beschreibung einer Welle werden die gleichen Größen wie zur Beschreibung von Schwingungen verwendet. Zusätzlich sind zwei weitere Begriffe für die Beschreibung von Wellen nützlich:
- Alle Punkte, die vom Ausgangspunkt einer Welle den jeweils gleichen zeitlichen Abstand haben, werden „Wellenfront“ genannt. Bei periodischen Wellen haben alle Punkte einer Wellenfront den gleichen Schwingungszustand („Phase“).
- Die so genannte Wellenlänge
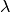 gibt die räumliche Periode einer
Welle an, das heißt den räumlichen Abstand zweier Wellenfronten. Die
Wellenlänge wird in Metern angegeben.
gibt die räumliche Periode einer
Welle an, das heißt den räumlichen Abstand zweier Wellenfronten. Die
Wellenlänge wird in Metern angegeben. - Die Ausbreitungsrichtung von Wellen ist stets senkrecht zu den einzelnen Wellenfronten.
Die Geschwindigkeit, mit der sich die einzelnen Wellenfronten ausbreiten, wird
als Ausbreitungs- oder Phasengeschwindigkeit  der Welle bezeichnet.[1] Die Richtung von
der Welle bezeichnet.[1] Die Richtung von  ist dabei stets senkrecht zur Wellenfront. In
vielen Materialien, insbesondere in Luft, breiten sich die einzelnen
Wellenfronten – nahezu unabhängig von der Frequenz der Wellen – mit der
gleichen Ausbreitungsgeschwindigkeit fort. Zwischen der Frequenz
ist dabei stets senkrecht zur Wellenfront. In
vielen Materialien, insbesondere in Luft, breiten sich die einzelnen
Wellenfronten – nahezu unabhängig von der Frequenz der Wellen – mit der
gleichen Ausbreitungsgeschwindigkeit fort. Zwischen der Frequenz 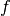 der
Welle und der Wellenlänge
der
Welle und der Wellenlänge 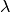 gilt dabei folgender wichtiger
Zusammenhang, der bisweilen auch „Wellenformel“ genannt wird:
gilt dabei folgender wichtiger
Zusammenhang, der bisweilen auch „Wellenformel“ genannt wird:
(1)¶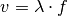
Anschaulich kann man sich diese Gleichung vorstellen, wenn man sich die
Wellenfronten unterschiedlicher Frequenz als zwei gemeinsam wandernde
Spaziergänger mit unterschiedlicher Schrittlänge vorstellt. Da sich beide mit
der gleichen Geschwindigkeit 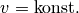 fortbewegen, muss der
Spaziergänger mit der kürzeren Schrittlänge eine entsprechend höhere
Schrittfrequenz haben.
fortbewegen, muss der
Spaziergänger mit der kürzeren Schrittlänge eine entsprechend höhere
Schrittfrequenz haben.
In der Akustik breiten sich entsprechend alle Schallwellen mit unterschiedlicher
Frequenz (Tonhöhe) in den meisten Materialien gleich schnell aus, in der Optik
breiten gilt das gleiche für Lichtwellen unterschiedlicher Frequenz (Farbe).
Für die Schallgeschwindigkeit in Luft gilt dabei ![c_0 = v_{\mathrm{Schall}}
\approx \unit[330]{\frac{m}{s}}](../../_images/math/725626744287d072c7298d446059927c729d9781.png) , für die Lichtgeschwindigkeit gilt
, für die Lichtgeschwindigkeit gilt ![c_0
= v_{\mathrm{Licht}} \approx \unit[3 \cdot 10^8]{\frac{m}{s}}](../../_images/math/fd5394a6c00396b32a43a6f1fec7e7ac7510334a.png) . Kennt man
die Frequenz oder die Wellenlänge einer Licht- oder Schallwelle, so kann man
mittels Gleichung (1) unmittelbar die
zugehörige fehlende Größe berechnen:
. Kennt man
die Frequenz oder die Wellenlänge einer Licht- oder Schallwelle, so kann man
mittels Gleichung (1) unmittelbar die
zugehörige fehlende Größe berechnen:
Beispiele:
Eine Schallwelle mit einer Frequenz von
![\unit[100]{Hz}](../../_images/math/ae4fe7d418b057a3daf664255c50b58d9373f3ed.png) (entspricht
einem Brummen von alten Lautsprechern) hat folgende Wellenlänge:
(entspricht
einem Brummen von alten Lautsprechern) hat folgende Wellenlänge:![v_{\mathrm{Schall}} = \lambda \cdot f \quad \Leftrightarrow \quad \lambda =
\frac{v_{\mathrm{Schall}}}{f} =
\frac{\unit[330]{\frac{m}{s}}}{\unit[100]{\frac{1}{s}}} = \unit[3,3]{m}
{\color{white}\qquad \qquad \qquad \qquad \quad 1}](../../_images/math/7ab748b4ddcbd29b7d3d00b9f9ea6df341b97f93.png)
Die Frequenzen von hörbarem Schall liegen etwa zwischen
![\unit[20]{Hz}](../../_images/math/5ff46f521f2f1b108af21f4ccea98cd215bebcc6.png) und
und ![\unit[20]{kHz}](../../_images/math/db4b1a43d004af08e2e75499105cb98714bbe03d.png) ; dies entspricht Wellenlängen von
; dies entspricht Wellenlängen von
![\unit[16,5]{m}](../../_images/math/9a35ded1b41dd9ba2041e6147a8a03dd6fb98501.png) bis rund
bis rund ![\unit[2]{cm}](../../_images/math/ba6e4780636db45f8cb56a7b28ed5f52b9f14ac2.png) .
.Eine Lichtwelle mit einer Wellenlänge von
![\unit[500]{nm} = \unit[500
\cdot 10 ^{-9}]{m}](../../_images/math/3cfb11b2dc091f48698bf933a35de9ef29d8e734.png) hat folgende Frequenz:
hat folgende Frequenz:![v_{\mathrm{Licht}} = \lambda \cdot f \quad \Leftrightarrow \quad f = \frac{v
_{\mathrm{Licht}}}{\lambda} = \frac{\unit[\;\;\;3 \cdot 10
^{+8}]{\frac{m}{s}}}{\unit[500 \cdot 10 ^{-9}]{m}} = \unit[600 \cdot 10
^{12}]{\frac{1}{s}} = \unit[600]{THz}](../../_images/math/3e13770596cd8f09aed702d2e78bde3063c55515.png)
Die Wellenlängen von sichtbarem Licht liegen zwischen etwa
![\unit[380]{nm}](../../_images/math/f74eb891904614de9c20f1895a79e28d12451ab7.png) und
und ![\unit[780]{nm}](../../_images/math/f7e1f13139927681e222fc9f39efb4a288237a49.png) ; dies entspricht Frequenzen
von etwa
; dies entspricht Frequenzen
von etwa ![\unit[789]{THz}](../../_images/math/d3d888590d55cdc9c1bbaa6ca4f6cfd4020b5d15.png) bis
bis ![\unit[384]{THz}](../../_images/math/66b27b112dc6b1ff3821d4f955d79a8740e4d32a.png) .
.
Die Ausbreitungsgeschwindigkeit  von Wellen hängt Materialeigenschaften
des Wellenträgers ab. Beispielsweise gelten folgende Zusammenhänge:
von Wellen hängt Materialeigenschaften
des Wellenträgers ab. Beispielsweise gelten folgende Zusammenhänge:
- Bei Longitudinalwellen in Flüssigkeiten gilt
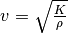 ,
wobei
,
wobei 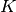 für den Kompressionsmodul der Flüssigkeit und
für den Kompressionsmodul der Flüssigkeit und 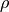 für
ihre Dichte steht.
für
ihre Dichte steht. - Bei Longitudinalwellen in Gasen gilt
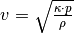 , wobei
, wobei  für den Adiabatenexponenten,
für den Adiabatenexponenten,  für
den Druck im Gas und
für
den Druck im Gas und 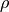 für dessen Dichte steht.
für dessen Dichte steht. - Bei Longitudinalwellen in festen Stäben gilt
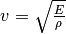 , wobei
, wobei 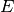 für den Elastizitätsmodul des
Festkörpers und
für den Elastizitätsmodul des
Festkörpers und 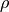 für dessen Dichte steht.
für dessen Dichte steht. - Bei Transversalwellen in festen Stäben gilt
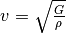 ,
wobei
,
wobei 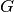 für den Schubmodul des Festkörpers und
für den Schubmodul des Festkörpers und 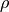 für dessen
Dichte steht.
für dessen
Dichte steht. - Bei Transversalwellen in dünnen Drähten gilt
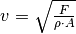 , wobei
, wobei  für die Spannkraft im Draht,
für die Spannkraft im Draht, 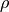 für dessen
Dichte und
für dessen
Dichte und  für dessen Querschnittsfläche steht.
für dessen Querschnittsfläche steht.
Aus den obigen Formeln folgt beispielsweise, dass die Schallgeschwindigkeit in Luft mit zunehmender Temperatur ebenfalls zunimmt, da die Dichte von Gasen bei gleichem Druck und steigender Temperatur abnimmt. Bei Musikinstrumenten hingegen ist vor allem die Spannkraft und die Querschnittsfläche der Seiten von Bedeutung: Tief klingende Saiten sind oftmals dicker, aus Materialien mit einer höheren Dichte gefertigt und/oder weniger stark gespannt.
In manchen Materialien ist die Ausbreitungsgeschwindigkeit  zudem
abhängig von der Frequenz
zudem
abhängig von der Frequenz 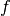 der Wellen. In diesem Fall laufen die
einzelnen Wellen auseinander, man spricht von Dispersion. Dieser Effekt wird
beispielsweise in der Optik zur Aufspaltung von weißem
Licht in Spektralfarben mittels eines Prismas genutzt.
der Wellen. In diesem Fall laufen die
einzelnen Wellen auseinander, man spricht von Dispersion. Dieser Effekt wird
beispielsweise in der Optik zur Aufspaltung von weißem
Licht in Spektralfarben mittels eines Prismas genutzt.
Superpositionsprinzip¶
Wellen können sich, ohne sich gegenseitig zu stören, zu einer resultierenden Welle überlagern. Sind die Frequenzen und Amplituden der einzelnen (Teil-)Wellen bekannt, so kann man daraus die resultierende Welle bestimmen.
Überlagern sich zwei sinusförmige Wellen mit gleicher Ausbreitungsrichtung und gleicher Frequenz, so entsteht wiederum eine sinusförmige Welle mit der gleichen Frequenz. Die Amplitude und Phase der resultierenden Schwingung ist von denen der einzelnen Wellen abhängig.
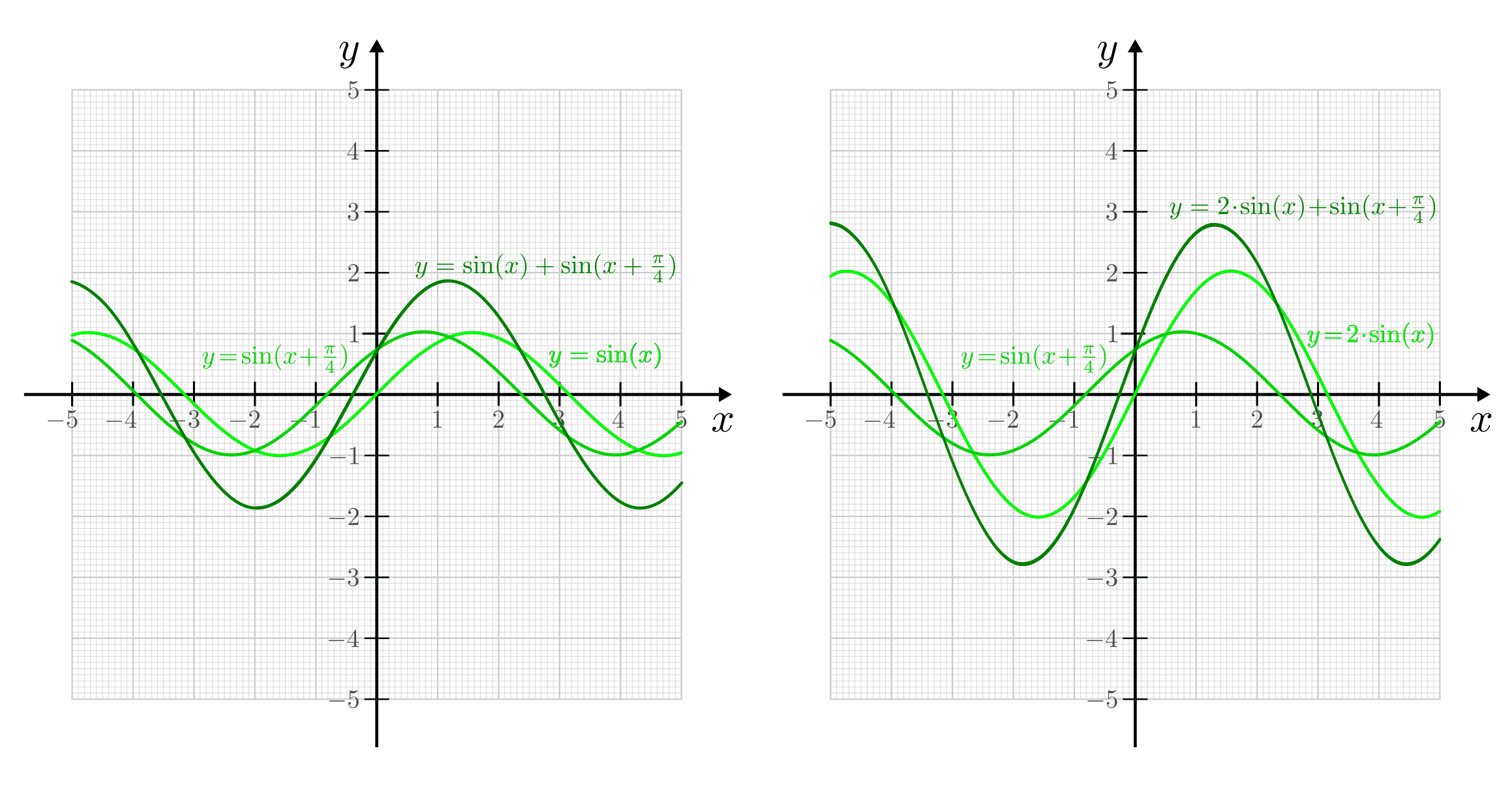
Überlagerung zweier sinusförmiger Wellen gleicher Frequenz und gleichen bzw. unterschiedlichen Amplituden.
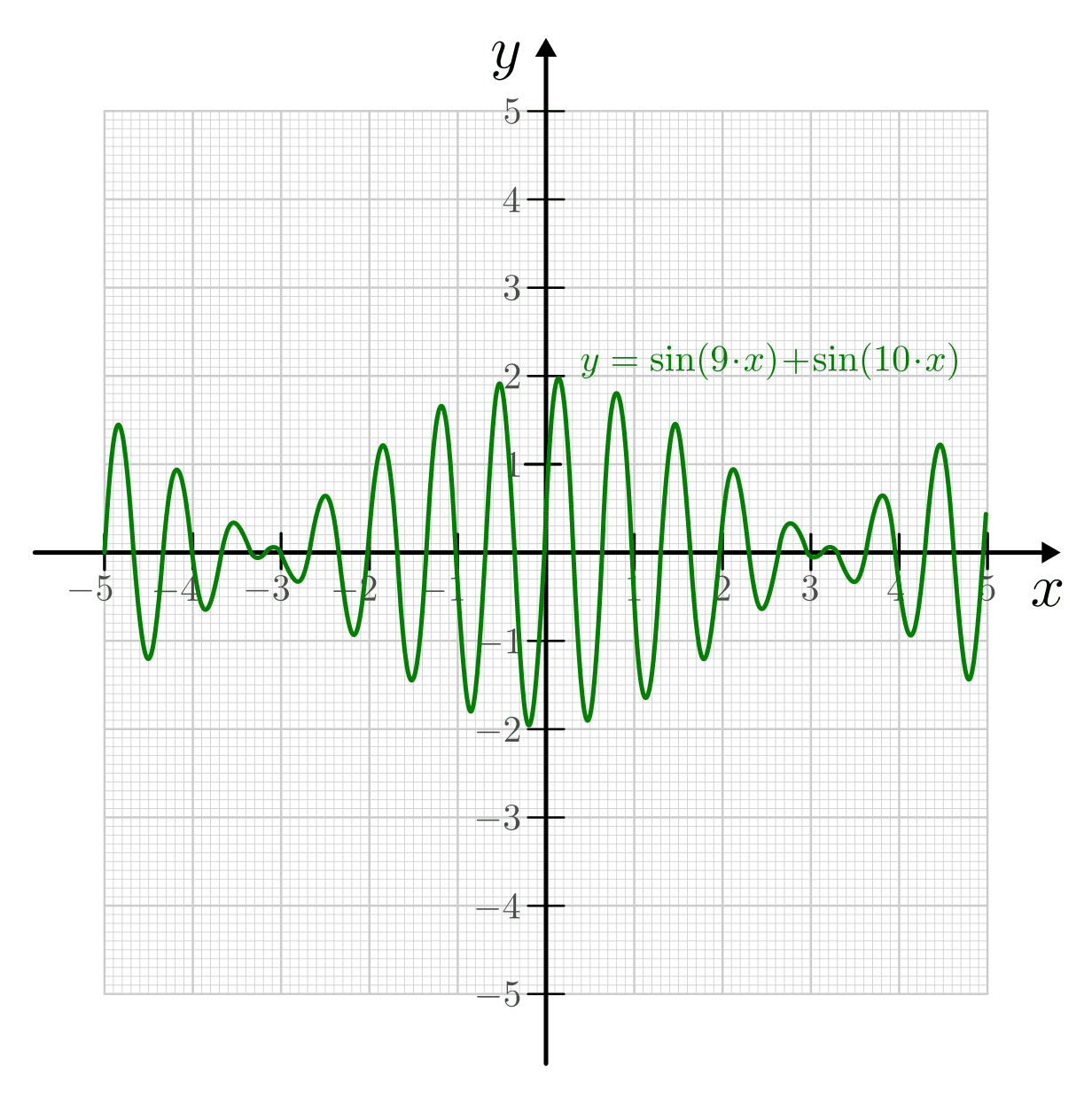
Überlagern sich zwei sinusförmige Wellen mit gleicher Ausbreitungsrichtung, aber unterschiedlicher Frequenz, so entsteht eine nicht-sinusförmige Welle. Die Amplitude und Form der resultierenden Schwingung ist wiederum von denen der einzelnen Wellen abhängig.
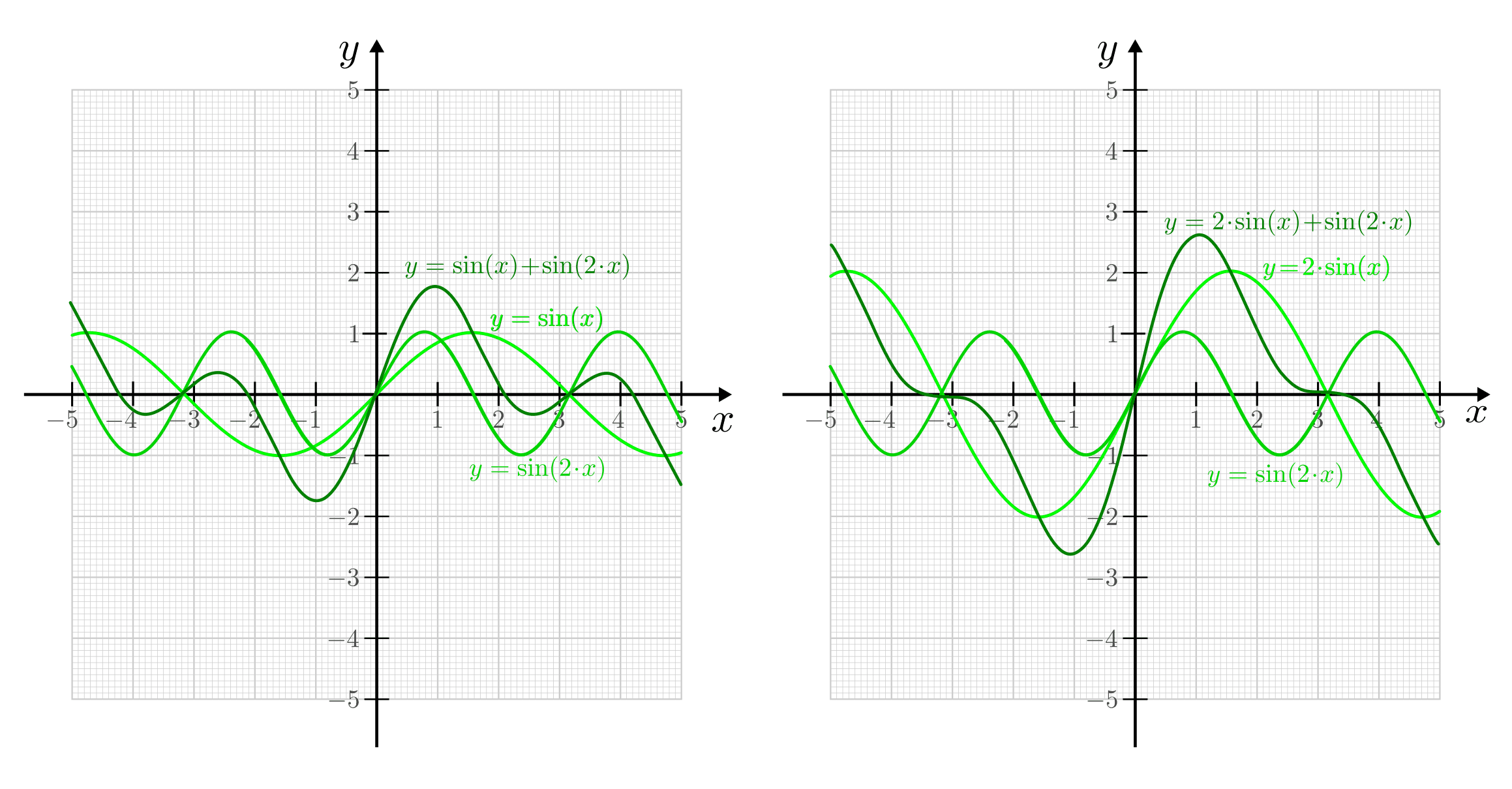
Überlagerung zweier sinusförmiger Wellen unterschiedlicher Frequenz und gleichen bzw. unterschiedlichen Amplituden.
Unterscheiden sich zwei Wellen mit gleicher Phase und gleicher Amplitude nur
geringfügig in ihrer Frequenz, so ergibt sich bei der Überlagerung beider Wellen
eine so genannte Schwebung. Hierbei handelt es sich um eine Welle mit der
mittleren Frequenz 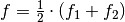 der beiden
Einzelschwingungen, deren Amplitude periodisch zwischen Null und der maximalen
Amplitude schwankt.
der beiden
Einzelschwingungen, deren Amplitude periodisch zwischen Null und der maximalen
Amplitude schwankt.
Je geringer der Frequenzunterschied der Teilwellen ist, desto länger wird die Dauer der Schwebung. Für die Frequenz der Schwebung gilt:
(2)¶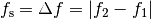
Schwebungen werden beispielsweise genutzt, um Klaviere oder Gitarren zu stimmen: Verklingt die Schwebung nicht schneller als die angeschlagenen Töne des Instruments, die in Übereinstimmung gebracht werden sollen, so ist das Instrument gut gestimmt.
Interferenz-Effekte¶
Treffen an einer Stelle zwei oder mehrere Wellen aus unterschiedlichen Richtungen aufeinander, so findet dort wiederum eine Überlagerung der einzelnen Wellenamplituden statt:
- Haben die einzelnen Wellen eine gleiche momentane Auslenkung (beide in positive oder beide in negative Auslenkungsrichtung), so überlagern sich die Wellen „konstruktiv“, das heißt die resultierende Amplitude ist größer als die Amplituden der einzelnen Wellen.
- Haben die einzelnen Wellen hingegen unterschiedliche Auslenkungsrichtungen, so überlagern sich die Wellen „destruktiv“; die resultierende Amplitude ist hierbei geringer als die Beträge der einzelnen Amplituden. Auch eine völlige Auslöschung zweier Teilwellen ist in diesem Fall möglich.
An jeder Stelle der Welle sind somit die Auslenkungszustände der Teilwellen unter Berücksichtigung des Vorzeichens zu addieren. Vereinfacht gesagt: Trifft ein „Wellenberg“ auf einen anderen „Wellenberg“, so ergibt sich ein höherer Wellenberg, trifft ein „Wellenberg“ auf ein „Wellental“, so löschen sich die Amplituden an dieser Stelle zumindest teilweise aus.
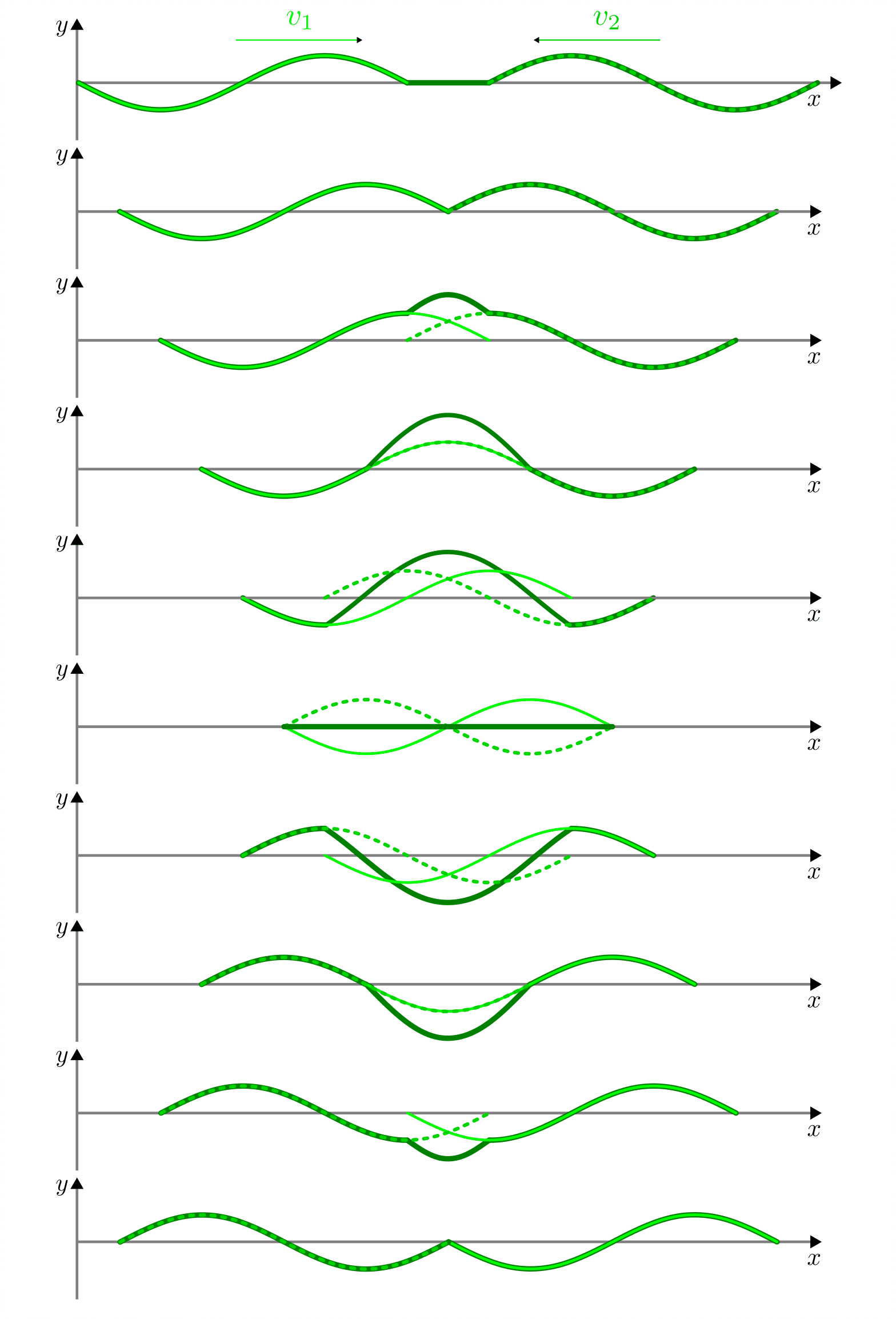
Interferenz zweier Wellen mit gleich großer Amplitude und entgegengesetzt
gleich großer Ausbreitungsgeschwindigkeit  .
.
Handelt es sich bei den aufeinander treffenden Wellen nicht nur um einen einzelnen Auslenkungszustand (Wellenberg bzw. Wellental, manchmal allgemein auch „Wellenpaket“ genannt), sondern um einen kontinuierlichen, nicht abbrechenden „Wellenzug“, so bezeichnet man das Ergebnis der Überlagerungen der Teilwellen als Interferenz.
Kohärenz und Gangunterschied
Dauerhaft bilden sich Interferenz-Effekte nur dann aus, wenn die sich überlagernden Wellen eine gleiche Frequenz und eine feste Phasenbeziehung zueinander haben. Die Wellen müssen also von gleich schnell schwingenden Erregern ausgehen, die sich relativ zueinander in Ruhe befinden, sich also nicht voneinander entfernen oder aufeinander zubewegen. Erfüllen zwei oder mehrere Wellenzüge diese beiden Bedingungen, so bezeichnet man sie als kohärent.
Werden beispielsweise, wie in der obigen Abbildung dargestellt, Wasserwellen durch zwei im gleichen Rhythmus eintauchende Stangen erzeugt, so kommen beide Teilwellen stets gleichzeitig an der Mittelsenkrechten zwischen den beiden Eintauchstellen an. Entlang dieser Linie überlagern sich beide Wellen somit stets konstruktiv, es treten dort also hohe Wellenberge auf, gefolgt von tiefen Wellentälern. Zusätzlich zur Mittelsenkrechten existieren noch weitere Linien, an denen es stets zu konstruktiver (oder auch destruktiver) Interferenz kommt.
Entscheidend dafür, ob es an einer Stelle zu konstruktiver oder destruktiver
Interferenz kommt, sind die beiden Weglängen 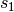 und
und 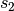 von den
beiden Ausgangspunkten der Welle zur betreffenden Stelle. Haben beide Wellen zu
Beginn den gleichen Auslenkungszustand (die gleiche Phase), so ergibt sich genau
dann ein Interferenz-Maximum, wenn sich die beiden Weglänge um ein Vielfaches
einer ganzen Wellenlänge unterscheiden. Es muss in diesem Fall also für den so
genannten „Gangunterschied“
von den
beiden Ausgangspunkten der Welle zur betreffenden Stelle. Haben beide Wellen zu
Beginn den gleichen Auslenkungszustand (die gleiche Phase), so ergibt sich genau
dann ein Interferenz-Maximum, wenn sich die beiden Weglänge um ein Vielfaches
einer ganzen Wellenlänge unterscheiden. Es muss in diesem Fall also für den so
genannten „Gangunterschied“ 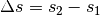 folgendes gelten:
folgendes gelten:
(3)¶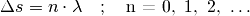
Diese Bedingung besagt anschaulich, dass beide Wellen exakt mit dem gleichen
Auslenkungszustand ankommen, auch wenn die eine Welle bis zum Ankunftsort
bereits ein paar Wellenberge und Wellentäler mehr durchlaufen hat. Beträgt der
Gangunterschied hingegen genau eine halbe Wellenlänge, so treffen die
Wellenberge der einen Welle auf die Wellentäler der anderen Welle, und man
erhält destruktive Interferenz. An einem Interferenz-Minimum muss also für den
Gangunterschied 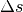 gelten:
gelten:
(4)¶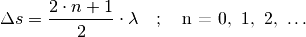
Durch 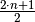 wird hierbei ein ungerades Vielfaches
einer halben Wellenlänge bezeichnet, also
wird hierbei ein ungerades Vielfaches
einer halben Wellenlänge bezeichnet, also 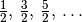 .
.
Stehende Wellen
Ein Sonderfall von Interferenz ergibt sich, wenn eine Welle auf ein festes Hindernis oder das Ende des Wellenträgers trifft. Kann sich die Welle nicht weiter ausbreiten, so wird sie reflektiert und läuft mit gleicher Ausbreitungsgeschwindigkeit in die entgegengesetzte Richtung. Dabei überlagert sich die reflektierte mit weiteren Wellen, die sich noch in der ursprünglichen Richtung bewegen.
Da die Frequenz der reflektierten Welle mit der Frequenz des ursprünglichen
Wellenzugs identisch ist, kann es wiederum zu konstruktiver Interferenz kommen,
wenn der Wellenträger eine zur Wellenlänge 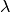 passende Wellenlänge
hat:
passende Wellenlänge
hat:
Ist der Wellenträger, beispielsweise ein Seil oder eine Saite eines Musikinstrumens, an beiden Enden fest eingespannt, so ergibt sich genau dann eine konstruktive Interferenz, wenn die Seillänge
 einem ganzzahligen
Vielfachen von einem Halben der Wellenlänge entspricht. Es muss also folgende
Bedingung gelten:
einem ganzzahligen
Vielfachen von einem Halben der Wellenlänge entspricht. Es muss also folgende
Bedingung gelten:(5)¶
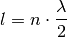
Schwingende Saiten haben also, im Gegensatz zu normalen Pendeln, nicht nur eine einzige Eigenfrequenz. Zusätzlich zur so genannten „Grundschwingung“ mit
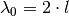 können weitere „Oberschwingungen“ auftreten,
wobei für die erste Oberschwingung
können weitere „Oberschwingungen“ auftreten,
wobei für die erste Oberschwingung 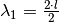 gilt, für die zweite
gilt, für die zweite 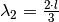 , für die dritte
, für die dritte
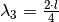 , usw.
, usw.Die Grundschwingung hat stets die größte Amplitude und ist ausschlaggebend für die Frequenz der sich ausbreitenden Welle. Die zusätzlich auftretenden Oberschwingungen hingegen modifizieren die Wellenkurve, so dass sich beispielsweise bei verschiedenen Musikinstrumenten auch dann unterschiedliche Klänge ergeben, wenn die Instrumente perfekt gestimmt sind und der gleiche „Ton“ gespielt wird.
Ist der Wellenträger, beispielsweise eine Stimmgabel oder ein schwingendes Metallplättchen, an einem Ende fest eingespannt und am anderen Ende lose, so ergibt sich genau dann eine konstruktive Interferenz, wenn die Länge
 des Objekts einem ganzzahligen Vielfachen von einem Viertel der Wellenlänge
entspricht. Es muss also folgende Bedingung gelten:
des Objekts einem ganzzahligen Vielfachen von einem Viertel der Wellenlänge
entspricht. Es muss also folgende Bedingung gelten:(6)¶
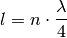
Dieser Zusammenhang gilt auch, wenn die Luftsäule in einem einseitig geschlosssenen Rohr zum Schwingen gebracht wird.
Ist der Wellenträger, beispielsweise bei einem Blasinstrument, an beiden Enden offen, so ergibt sich genau dann eine konstruktive Interferenz, wenn die Länge
 des Objekts einem ganzzahligen Vielfachen von einem Halben der
Wellenlänge entspricht. Es muss also – ebenso wie bei beidseitig fest
eingespannten Wellenträgern – folgende Bedingung gelten:
des Objekts einem ganzzahligen Vielfachen von einem Halben der
Wellenlänge entspricht. Es muss also – ebenso wie bei beidseitig fest
eingespannten Wellenträgern – folgende Bedingung gelten:(7)¶
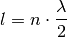
Die Länge des Wellenträgers ist, beispielsweise bei Musikinstrumenten, also
maßgeblich für die Wellenlänge 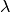 der Grundschwingung. Welche
Frequenz
der Grundschwingung. Welche
Frequenz 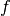 die stehende Welle und somit der entstehende Ton hat, hängt
allerdings wegen
die stehende Welle und somit der entstehende Ton hat, hängt
allerdings wegen 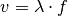 beziehungsweise
beziehungsweise 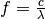 auch von der Ausbreitungsgeschwindigkeit
auch von der Ausbreitungsgeschwindigkeit  der Welle
auf dem Wellenträger ab.
der Welle
auf dem Wellenträger ab.
Mathematische Beschreibung von Wellen¶
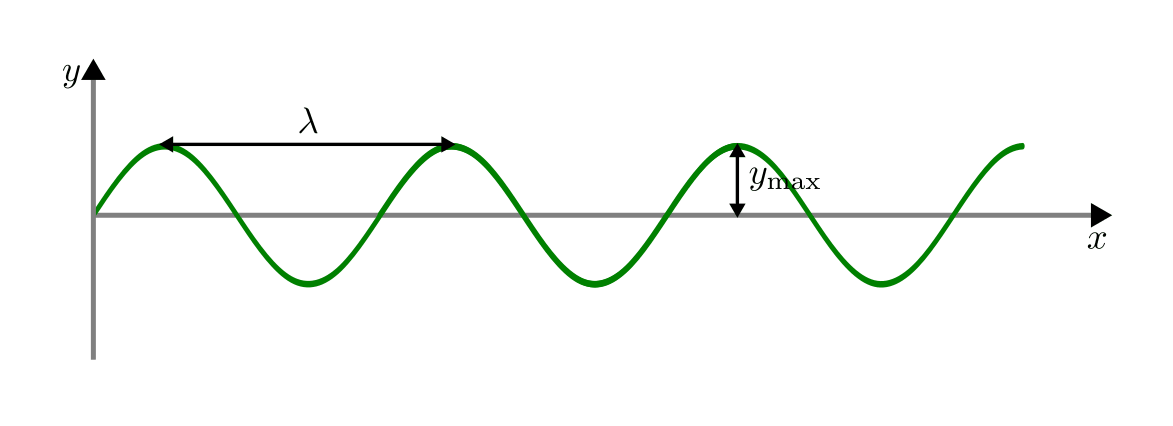
Im folgenden werden Wellen betrachtet, die räumlich ein sinus-förmiges
Ausbreitungsmuster haben. Beginnt die Welle am Koordinatenursprung 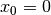 mit der Auslenkung
mit der Auslenkung 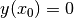 , so ergibt sich ein Wellenausbreitung, wie
sie in der folgenden Abbildung dargestellt ist.
, so ergibt sich ein Wellenausbreitung, wie
sie in der folgenden Abbildung dargestellt ist.
In einer Entfernung von einem ganzzahligen Vielfachen der Wellenlänge
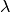 wiederholt sich jeweils das Wellenmuster. Die Welle hat aus
räumlicher Sicht also eine Periode der Länge
wiederholt sich jeweils das Wellenmuster. Die Welle hat aus
räumlicher Sicht also eine Periode der Länge 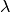 ; zugleich hat jede
Sinusfunktion eine Periode von
; zugleich hat jede
Sinusfunktion eine Periode von 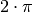 . Die Welle kann somit
durch folgende Formel charakterisiert werden:
. Die Welle kann somit
durch folgende Formel charakterisiert werden:
(8)¶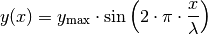
Hierbei bezeichnet 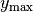 die Amplitude der Welle. Ist
die Amplitude der Welle. Ist
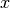 ein ganzzahliges Vielfaches von
ein ganzzahliges Vielfaches von 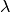 , so wird das Argument
der Sinus-Funktion entsprechend zu einem ganzzahligen Vielfachen von
, so wird das Argument
der Sinus-Funktion entsprechend zu einem ganzzahligen Vielfachen von 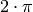 . Beginnt die Welle bei
. Beginnt die Welle bei 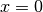 mit dem Wert
mit dem Wert 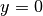 , so
genügt bereits die obige Gleichung zur Beschreibung der Welle, ansonsten muss
im Argument der Sinusfunktion noch ein anfänglicher Phasenwinkel
, so
genügt bereits die obige Gleichung zur Beschreibung der Welle, ansonsten muss
im Argument der Sinusfunktion noch ein anfänglicher Phasenwinkel
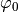 dazu addiert werden.
dazu addiert werden.
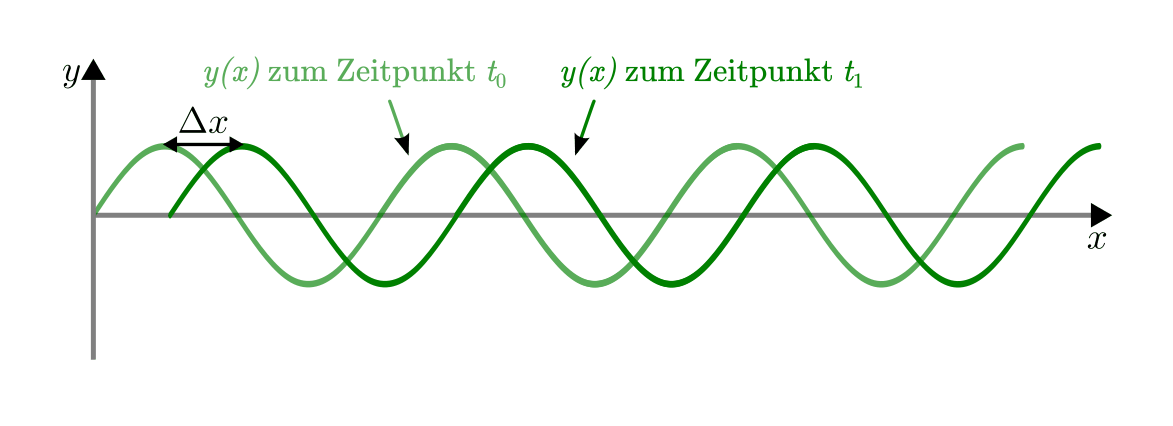
Wellenmuster bleiben – abgesehen von stehenden Wellen – allerdings nicht an
Ort und Stelle, sondern bewegen sich im Laufe der Zeit weiter. Bewegt sich die
Welle beispielsweise in positiver 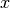 -Richtung, so wandert das
Wellenmuster in der Zeit
-Richtung, so wandert das
Wellenmuster in der Zeit 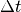 um die Länge
um die Länge 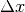 weiter.
weiter.
Für die „Verschiebung“ der Welle um 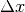 gilt:
gilt:
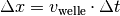
Diese Beziehung ist nützlich, um den Auslenkungszustand einer sinus-förmigen
Welle an jedem beliebigen Ort und zu jeder beliebigen Zeit zu bestimmen: Zum
Zeitpunkt 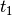 hat die Welle an der Stelle
hat die Welle an der Stelle 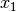 nämlich genau die
gleiche Auslenkung, die sie zum Zeitpunkt
nämlich genau die
gleiche Auslenkung, die sie zum Zeitpunkt 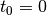 an der Stelle
an der Stelle 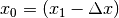 hatte. Es gilt somit:
hatte. Es gilt somit:
![y(x,t) &= y_{\mathrm{max}} \cdot \sin{\left(2 \cdot \pi \cdot \frac{x -
\Delta x}{\lambda}\right)} \\[6pt]
&= y_{\mathrm{max}} \cdot \sin{\left(\frac{2 \cdot \pi}{\lambda} \cdot
(x-\Delta x)\right)} \\[6pt]
&= y_{\mathrm{max}} \cdot \sin{\left(\frac{2 \cdot \pi}{\lambda} \cdot (x-
v_{\mathrm{welle}} \cdot t)\right)}](../../_images/math/c6b823e20914fbf3ee03d605695b49a4bcb6bb27.png)
Hierbei wurde vereinfacht  für die Differenz
für die Differenz 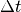 zwischen
dem Zeitpunkt
zwischen
dem Zeitpunkt  und dem Startpunkt
und dem Startpunkt 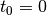 geschrieben. Die
Gleichung kann weiter umgeformt werden, wenn man für
geschrieben. Die
Gleichung kann weiter umgeformt werden, wenn man für  die Wellenbeziehung
die Wellenbeziehung 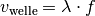 einsetzt:
einsetzt:
![y(x,t) &= y_{\mathrm{max}} \cdot \sin{\left(\frac{2 \cdot \pi}{\lambda}
\cdot (x- \lambda \cdot f \cdot t)\right)} \\[6pt]
&= y_{\mathrm{max}} \cdot \sin{\left(2 \cdot \pi \cdot
\left(\frac{x}{\lambda}- \cdot f \cdot t\right)\right)}](../../_images/math/e396b7af3ed009e743796ee600c7a804c14de9ca.png)
Im zweiten Rechenschritt wurde der Faktor 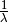 in die
innere Klammer hinein multipliziert. Schreibt man in dieser Form für die
Frequenz
in die
innere Klammer hinein multipliziert. Schreibt man in dieser Form für die
Frequenz 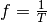 , so wird die räumliche sowie zeitliche Periode
der Welle deutlich:
, so wird die räumliche sowie zeitliche Periode
der Welle deutlich:
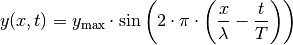
Die Welle fängt immer wieder dann von Neuem an, wenn 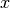 ein Vielfaches der
Wellenlänge
ein Vielfaches der
Wellenlänge 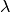 ist (räumliche Periode), oder wenn
ist (räumliche Periode), oder wenn  ein
Vielfaches der Schwingungsdauer
ein
Vielfaches der Schwingungsdauer 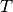 ist (zeitliche Periode).
ist (zeitliche Periode).
Für praktische Rechnungen ist es noch „handlicher“, auch den Faktor 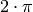 im Argument der Sinus-Funktion in die Klammer hinein zu
multiplizieren. Man erhält hierbei:
im Argument der Sinus-Funktion in die Klammer hinein zu
multiplizieren. Man erhält hierbei:
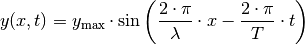
In dieser Darstellung entspricht der Term 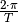 gerade
der Kreisfrequenz
gerade
der Kreisfrequenz  der Welle; diese gibt an, mit welcher
Geschwindigkeit die Welle in der Zeigerdarstellung
oszilliert. Entsprechend bezeichnet man den Term
der Welle; diese gibt an, mit welcher
Geschwindigkeit die Welle in der Zeigerdarstellung
oszilliert. Entsprechend bezeichnet man den Term 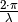 als so genannte „Kreiswellenzahl“
als so genannte „Kreiswellenzahl“ 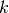 . Damit ergibt sich
für den Auslenkungszustand einer Welle folgende „einfache“ Form der Gleichung:
. Damit ergibt sich
für den Auslenkungszustand einer Welle folgende „einfache“ Form der Gleichung:
(9)¶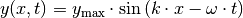
Die Kreiswellenzahl 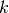 gibt an, wie viele Wellen in eine bestimmte
Längeneinheit (beispielsweise
gibt an, wie viele Wellen in eine bestimmte
Längeneinheit (beispielsweise 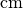 oder
oder 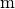 ) hinein
passen. Je kürzer also die Wellenlänge
) hinein
passen. Je kürzer also die Wellenlänge 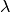 einer Welle ist, desto
größer ist also ihr
einer Welle ist, desto
größer ist also ihr 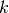 -Wert. Für Mikrowellen ist beispielsweise
-Wert. Für Mikrowellen ist beispielsweise 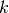 in der Größenordnung von etwa
in der Größenordnung von etwa 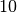 je
je 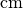 , bei Lichtwellen in der
Größenordnung von über
, bei Lichtwellen in der
Größenordnung von über 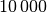 je
je 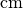 .
.
Anmerkungen:
| [1] | In der Akustik und Optik wird die Ausbreitungsgeschwindigkeit (Schall-
bzw. Lichtgeschwindigkeit) üblicherweise mit  anstelle anstelle  bezeichnet.
bezeichnet. |



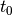 .
.