Wellenoptik¶
Unter bestimmten Bedingungen zeigt Licht Welleneigenschaften, die mit dem vereinfachten Modell von „Lichtstrahlen“ nicht erklärbar sind. Um beispielsweise auch Farbspektren, Interferenz- und Polarisationserscheinungen beschreiben zu können, geht man in der „modernen“ Optik von einem Wellenmodell des Lichts aus.
Lichtbeugung und Interferenz¶
Wird Licht durch die Öffnung einer Blende so begrenzt, dass nur ein schmales Lichtbündel die Blende passieren kann, so dürfte gemäß der Strahlenoptik kein Licht außerhalb dieses Bündels auftreten. Tatsächlich weicht die Ausbreitungsrichtung des Lichts allerdings vom geradlinigen Verlauf ab, so dass an nahezu allen Stellen hinter der Blende eine gewisse Menge an Licht anzutreffen ist. Man sag, dass Licht, ähnlich wie eine Wasserwelle, an den Kanten eines Hindernisses „gebeugt“ wird.
Das Huygensche Prinzip
Im Jahr 1678 veröffentlichte Christian Huygens ein Buch zur Wellentheorie des Lichts. Darin beschrieb er unter anderem das heute nach ihm benannte Prinzip der Elementarwellen:
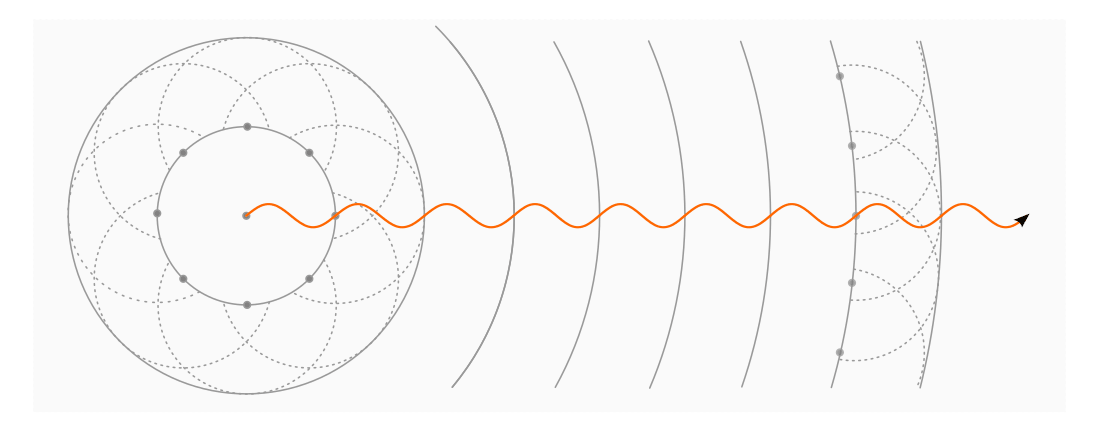
Jeder Punkt einer Wellenfront stellt selbst wiederum einen Ausgangspunkt für eine neue, kreisförmig in alle Richtungen verlaufende Welle dar. Die einzelnen Wellen überlagern sich dabei zur nächsten Wellenfront.
Die Senkrechte auf den Wellenfronten entspricht der Ausbreitungsrichtung der Welle.
Unter einer Wellenfront versteht man die Menge aller Punkte, die zu einem bestimmten Zeitpunkt eine gleiche Phasenlage aufweisen, also beispielsweise zu einem bestimmten Zeitpunkt einen Wellenberg darstellen. Das Huygensche Prinzip kann also als eine Art geometrische Konstruktionshilfe aufgefasst werden, die beispielsweise zum Zeichnen der Ausbreitung einer Welle genutzt werden kann. Ist eine gleichmäßig verlaufende Welle weit vom ursprünglichen Erregerzentrum entfernt, so verlaufen die Wellenfronten beziehungsweise die Ausbreitungsrichtungen nahezu geradlinig und parallel.
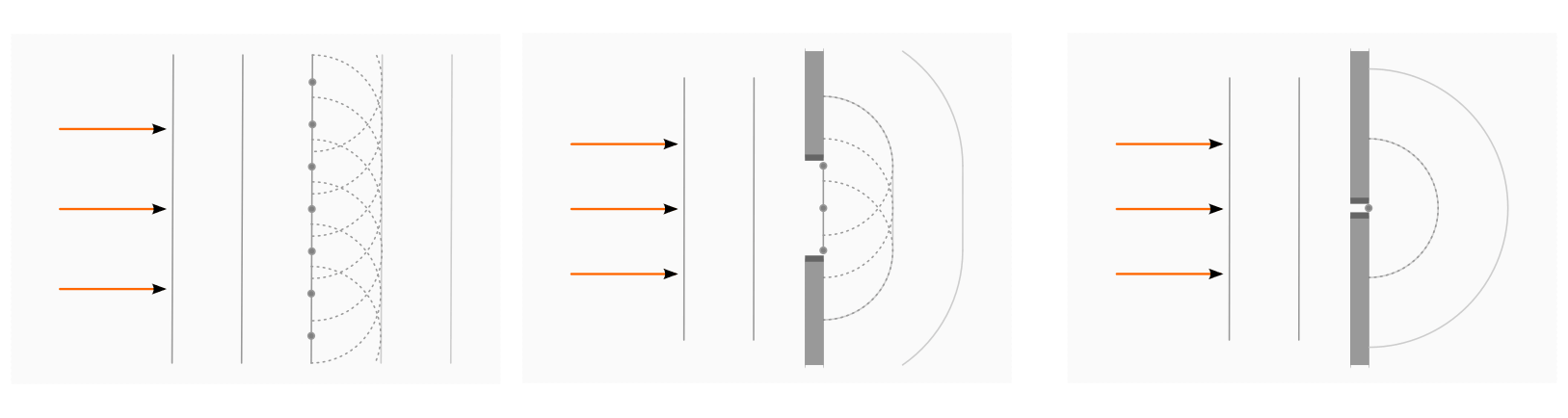
Trifft eine Wellenfront hingegen auf ein (nicht zu kleines) Hindernis, beispielsweise den Rand einer Blende, so tritt eine Beugung des Lichts auf. Das Licht kann sich dabei auch in Bereiche hinein ausbreiten, die nach der Strahlentheorie dunkle „Schattenräume“ darstellen würden. Wohl am deutlichsten zeigt sich diese Eigenschaft an einem dünnen Spalt, dessen Breite in etwa so groß wie die Wellenlänge der eintreffenden Wellen ist. In diesem Fall entstehen hinter der Öffnung erneut kreisförmig verlaufende Wellen, welche die Spaltöffnung der Blende als gemeinsames Zentrum haben.[1]
Beugung und Interferenz an einem Doppelspalt
Hat eine Blende zwei schmale, im Abstand 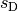 voneinander
entfernte Öffnungen, so teilt sich eine einfallende Lichtwelle hinter der Blende
in zwei kreisförmige, von den beiden Öffnungen aus verlaufende Wellen auf. Diese
Wellen überlagern sich, so dass es an bestimmten Stellen zu konstruktiver, an
anderen Stellen zu destruktiver Interferenz kommt. Bestrahlt man den Doppelspalt
beispielsweise mit einem Laser und bringt in einigen Metern hinter der Blende
einen optischen Schirm an, so lässt sich auf diesem ein hell-dunkles
Streifenmuster in der Farbe des Lasers erkennen.
voneinander
entfernte Öffnungen, so teilt sich eine einfallende Lichtwelle hinter der Blende
in zwei kreisförmige, von den beiden Öffnungen aus verlaufende Wellen auf. Diese
Wellen überlagern sich, so dass es an bestimmten Stellen zu konstruktiver, an
anderen Stellen zu destruktiver Interferenz kommt. Bestrahlt man den Doppelspalt
beispielsweise mit einem Laser und bringt in einigen Metern hinter der Blende
einen optischen Schirm an, so lässt sich auf diesem ein hell-dunkles
Streifenmuster in der Farbe des Lasers erkennen.
Um dieses Interferenzmuster erklären zu können, muss die Phasenlage der beiden
vom Spalt ausgehenden Lichtwellen betrachtet werden. An ihren Ausgangspunkten
haben beide die gleiche Phase, da eine aus weiter Entfernung senkrecht
eintreffende Lichtwelle beide Spalte gleichzeitig erreicht. Bei einfarbigem
Licht weisen beide Wellen zudem eine gleiche Wellenlänge 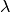 auf.
Der einzige Unterschied zwischen beiden Wellen liegt somit darin, dass sie von
zwei unterschiedlichen Zentren ausgehen und daher, von einem Blickwinkel
auf.
Der einzige Unterschied zwischen beiden Wellen liegt somit darin, dass sie von
zwei unterschiedlichen Zentren ausgehen und daher, von einem Blickwinkel
 aus gesehen, einen so genannten „Gangunterschied“
aus gesehen, einen so genannten „Gangunterschied“ 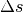 aufweisen. Damit ist gemeint, dass eine der beiden Wellen zu Beginn ihrer
Ausbreitung eine um
aufweisen. Damit ist gemeint, dass eine der beiden Wellen zu Beginn ihrer
Ausbreitung eine um 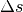 längere Wegstrecke zurücklegen muss.
längere Wegstrecke zurücklegen muss.
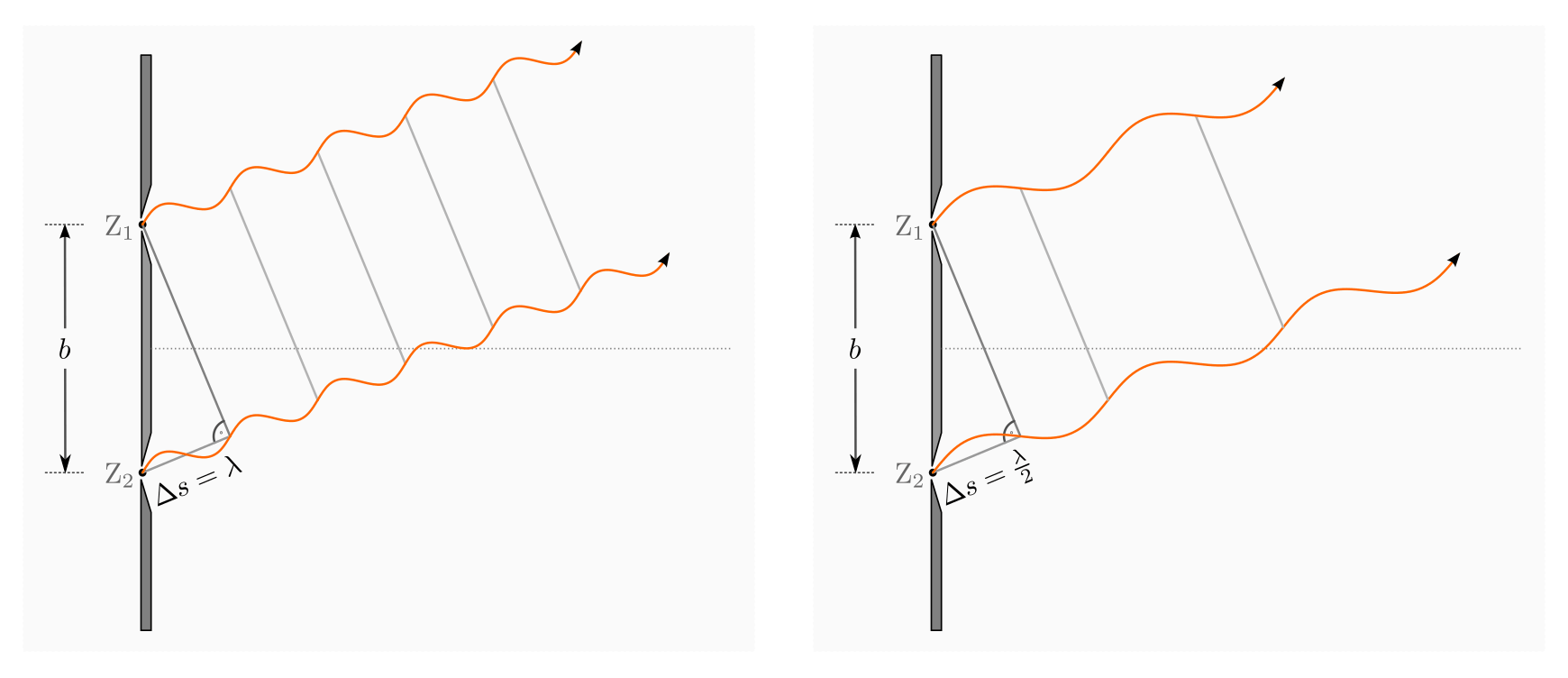
Ist der Gangunterschied 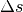 gleich einer ganzen Wellenlänge
gleich einer ganzen Wellenlänge
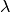 , so verlaufen die Lichtwellen anschließend in stets gleicher
Phase, es tritt also konstruktive Interferenz auf. Die Bedingung für ein
Intensitätsmaximum ist ebenso erfüllt, wenn der Gangunterschied
, so verlaufen die Lichtwellen anschließend in stets gleicher
Phase, es tritt also konstruktive Interferenz auf. Die Bedingung für ein
Intensitätsmaximum ist ebenso erfüllt, wenn der Gangunterschied 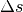 ein ganzzahliges Vielfaches
ein ganzzahliges Vielfaches 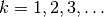 der Wellenlänge
der Wellenlänge
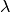 beträgt:
beträgt:
(1)¶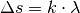
Entlang der Mittellinie tritt (für beliebige Wellenlängen) an allen Stellen
konstruktive Interferenz ein, da alle Punkte auf dieser Linie von beiden
Spaltöffnungen gleich weit entfernt sind, der Gangunterschied für beide Wellen
somit gleich Null ist. Das zugehörige Helligkeitsmaximum wird auch als „nulltes
Maximum“ bezeichnet, da es dem Gangunterschied 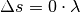 entspricht.
entspricht.
Ist der Gangunterschied 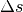 hingegen gleich der Hälfte
der Wellenlänge
hingegen gleich der Hälfte
der Wellenlänge 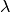 (oder einem ungeradzahligen Vielfachen), so
verlaufen die Lichtwellen anschließend in Gegenphase, es tritt also destruktive
Interferenz auf.
(oder einem ungeradzahligen Vielfachen), so
verlaufen die Lichtwellen anschließend in Gegenphase, es tritt also destruktive
Interferenz auf.
Wie weit die hellen und dunklen Streifen auf dem Schirm auseinander liegen bzw.
unter welchen Winkeln 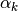 sie erscheinen, ist somit von der
Wellenlänge
sie erscheinen, ist somit von der
Wellenlänge 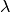 abhängig. Bezüglich des Winkels
abhängig. Bezüglich des Winkels 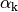 gelten zudem folgende geometrische Beziehungen:
gelten zudem folgende geometrische Beziehungen:
Der Abstand
![s \approx \unit[5]{m}](../_images/math/95b6b5885e03fe24b5215e24fa82f6013f747f3b.png) zwischen dem Doppelspalt und dem
Schirm ist sehr viel größer als der Abstand
zwischen dem Doppelspalt und dem
Schirm ist sehr viel größer als der Abstand ![b \approx \unit[0,1]{mm}](../_images/math/3c77e37c25d45d9d81c88f830bb97665441767e0.png) der beiden Spaltöffnungen voneinander; vom Schirm aus gesehen erscheinen beide
Spaltöffnungen in sehr guter Näherung unter dem gleichen Winkel
der beiden Spaltöffnungen voneinander; vom Schirm aus gesehen erscheinen beide
Spaltöffnungen in sehr guter Näherung unter dem gleichen Winkel
 . Somit gilt:
. Somit gilt: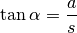
Dabei bezeichnet
 den Abstand des auf dem Schirm betrachteten
Maximums von der Mittellinie.
den Abstand des auf dem Schirm betrachteten
Maximums von der Mittellinie.
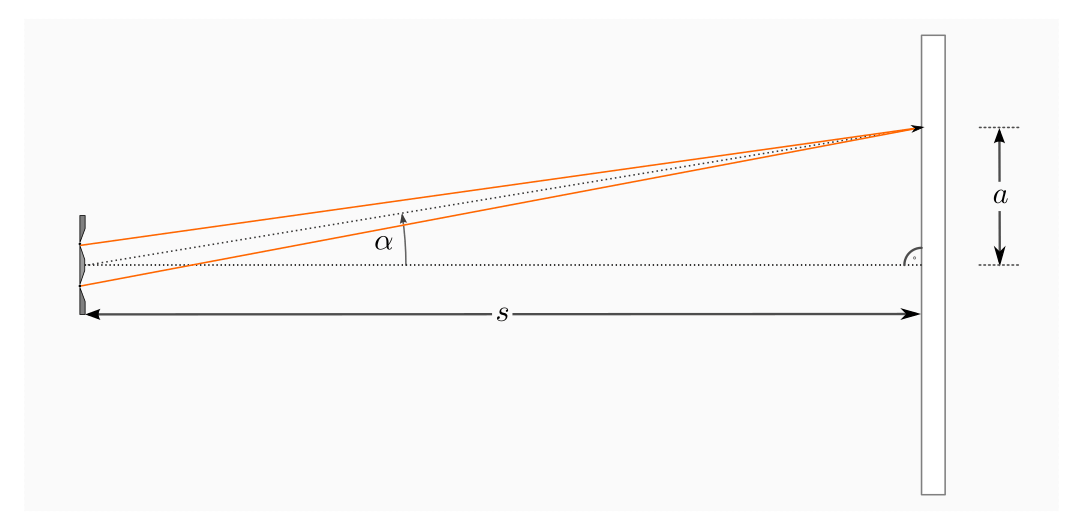
Struktureller Zusammenhang zwischen dem Betrachtungswinkel  ,
dem Schirmabstand
,
dem Schirmabstand  und dem Abstand
und dem Abstand  eines Maximums von der
Mittellinie.
eines Maximums von der
Mittellinie.
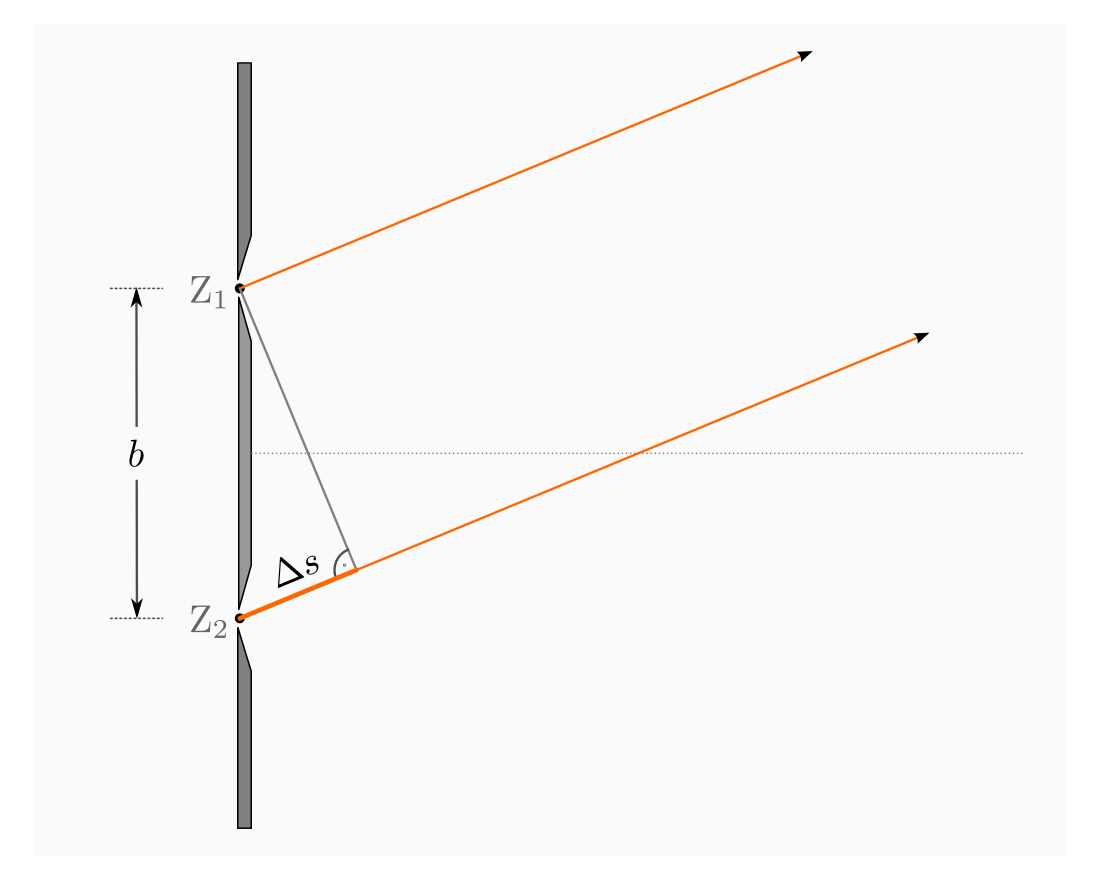
Betrachtet man in der obigen Abbildung das an den beiden Spaltöffnungen anliegende, rechtwinklige Dreieck, so kann man folgenden Zusammenhang zwischen dem Winkel
 , dem Spaltabstand
, dem Spaltabstand 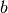 und dem Gangunterschied
und dem Gangunterschied
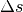 erkennen:
erkennen: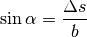
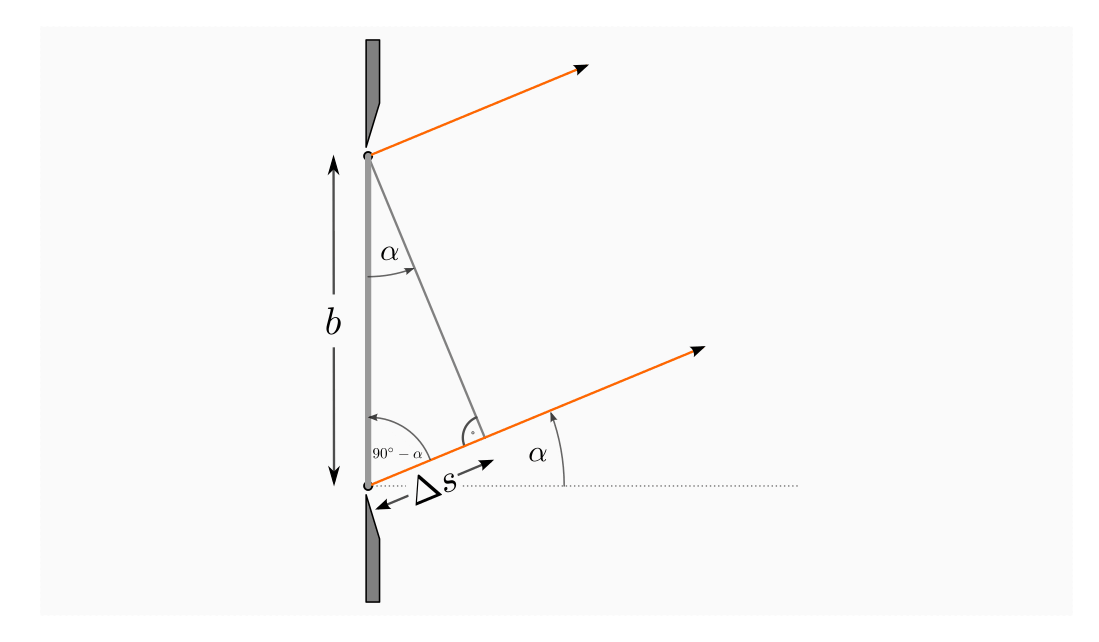
Struktureller Zusammenhang zwischen dem Betrachtungswinkel  ,
dem Gangunterschied
,
dem Gangunterschied 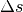 und dem Doppelspaltabstand
und dem Doppelspaltabstand 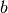 .
.
Da der Winkel  bei fast allen Doppelspalt-Versuchen sehr klein ist
bei fast allen Doppelspalt-Versuchen sehr klein ist
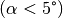 , kann in sehr guter Näherung folgende
Kleinwinkelnäherung verwendet werden:
, kann in sehr guter Näherung folgende
Kleinwinkelnäherung verwendet werden:
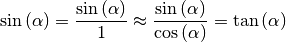
Mit dieser Näherung für kleine Winkel lassen sich die obigen Zusammenhänge und die Bedingung (1) für Intensitätsmaxima zu einer einzigen Formel zusammenfassen:
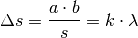
beziehungsweise, wenn man die Wellenlänge des Lichts bestimmen möchte:[2]
(2)¶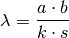
Ist der Doppelspalt-Abstand 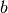 bekannt, so kann man also mittels einer
einfachen Messung der Entfernung
bekannt, so kann man also mittels einer
einfachen Messung der Entfernung  zwischen Doppelspalt und Schirm und
des Abstands
zwischen Doppelspalt und Schirm und
des Abstands  eines frei wählbaren Maximums
eines frei wählbaren Maximums 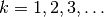 von
der Mittellinie auf dem Schirm unmittelbar die Wellenlänge des Lichts berechnet
werden.
von
der Mittellinie auf dem Schirm unmittelbar die Wellenlänge des Lichts berechnet
werden.
Beispiel:
Ein Doppelspalt wird mit einem roten Laserstrahl beleuchtet. Bei einem Schirmabstand von
![s = \unit[5,00]{m}](../_images/math/76f9c8aebed0d232e9aabd73d1b71aa914266421.png) erscheint auf dem Schirm das
erscheint auf dem Schirm das
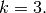 Maximum in einem Abstand
Maximum in einem Abstand ![a = \unit[0,10]{m}](../_images/math/a605834cd0e0964aaf9a2c6e807ee4afd0cfadc9.png) von der
Mittellinie. Hat die dabei verwendete Blende einen Doppelspaltabstand von
von der
Mittellinie. Hat die dabei verwendete Blende einen Doppelspaltabstand von
![b = \unit[0,1]{mm} = \unit[10 ^{-4}]{m}](../_images/math/e9009c456e858bc7debeec835ac3bd41a4bd7c30.png) , so gilt für die Wellenlänge
des Lichts:
, so gilt für die Wellenlänge
des Lichts:![\lambda = \frac{a \cdot b}{k \cdot s} = \frac{\unit[10 ^{-1}]{m} \cdot
\unit[10 ^{-4}]{m}}{3 \cdot \unit[5]{m}} \approx \unit[667 \cdot
10^{-9}]{m}](../_images/math/ef0a6a4d19f6c6b6f76f23d396ba67d7103695d1.png)
Die Wellenlänge des roten Laserlichts beträgt somit rund
![\unit[667]{nm}](../_images/math/94af1ca38afc625d1eebc2c1b8d803631cf616a8.png) .
.
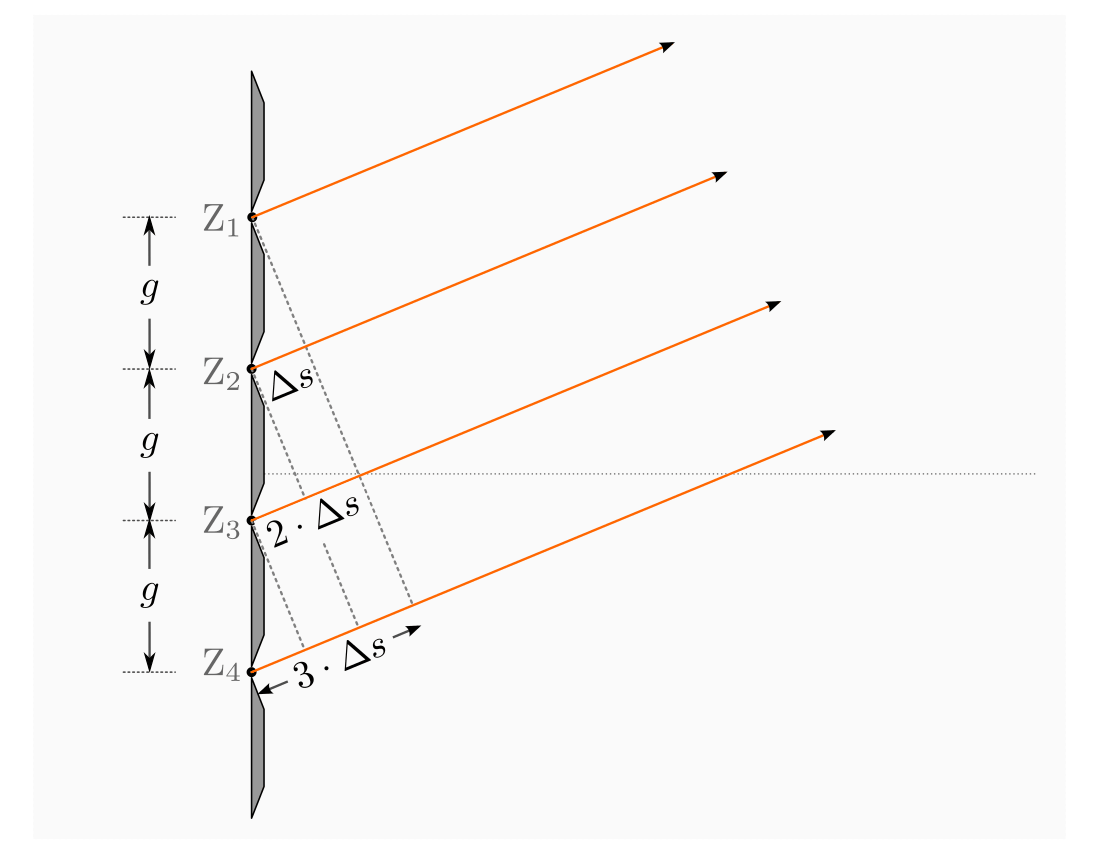
Beugung und Interferenz an einem Gitter
In der Praxis verwendet man anstelle eines Doppelspalts üblicherweise ein
optisches Gitter. Ein solches besteht aus sehr vielen spaltartige Öffnungen, die
regelmäßig im geringem Abstand voneinander angeordnet sind. Gute optische Gitter
können etwa eine Anzahl von 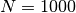 Spalten je Millimeter aufweisen. Für
den Abstand
Spalten je Millimeter aufweisen. Für
den Abstand 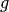 zwischen den den lichtdurchlässigen Bereichen gilt somit:
zwischen den den lichtdurchlässigen Bereichen gilt somit:
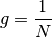
Der Gitterabstand beträgt für ![N=\unit[1000]{\frac{1}{mm}} = \unit[1 \cdot
10^6]{\frac{1}{m}}](../_images/math/454dcb47da61379bf782d8616fd99f926f14868c.png) genau
genau ![g=\unit[1 \cdot 10 ^{-6}]{m}](../_images/math/1f404437c10747f4d8922f65fa18f62528b59d94.png) , also einen
Mikrometer. Diese „Feinheit“ bewirkt, dass die einzelnen Interferenzmaxima um
einen größeren Winkel
, also einen
Mikrometer. Diese „Feinheit“ bewirkt, dass die einzelnen Interferenzmaxima um
einen größeren Winkel  aufgefächert werden und so auf dem Schirm
weniger „verschmieren“. Sie können auf dem Schirm, etwas umgangssprachlich
formuliert, in besserer Auflösung betrachtet werden.
aufgefächert werden und so auf dem Schirm
weniger „verschmieren“. Sie können auf dem Schirm, etwas umgangssprachlich
formuliert, in besserer Auflösung betrachtet werden.
Für die Lichtbeugung an einem optischen Gitter gelten grundsätzlich die gleichen
Gesetzmäßigkeiten und Formeln wie bei der Lichtbeugung an einem Doppelspalt; es
muss lediglich statt des Doppelspaltsabstands 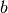 der Gitterabstand
der Gitterabstand
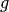 in die jeweilige Formel eingesetzt werden. Die Wellenlänge eines am
Gitter interferierenden, einfarbigen Lichtstrahls kann also – in Analogie zu
Gleichung (2) – unmittelbar anhand des
Gitterabstands
in die jeweilige Formel eingesetzt werden. Die Wellenlänge eines am
Gitter interferierenden, einfarbigen Lichtstrahls kann also – in Analogie zu
Gleichung (2) – unmittelbar anhand des
Gitterabstands 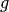 , dem Abstand
, dem Abstand  zwischen Gitter und Schirm und
dem Abstand
zwischen Gitter und Schirm und
dem Abstand  des
des 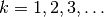 -ten Maximums von der
Mittellinie bestimmt werden:
-ten Maximums von der
Mittellinie bestimmt werden:
(3)¶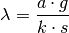
Verwendet man für Interferenzversuche an einem optischen Gitter kein Laserlicht, sondern ein anderes monochromatisches Licht, so muss das auf das Gitter einfallende Lichtstrahl zuvor durch einen einzelnen dünnen Spalt (eine schmale Blende) begrenzt werden. Die Spaltöffnung wirkt in diesem Fall in guter Näherung wie eine einzige punktförmige Lichtquelle, so dass die einzelnen Lichtwellen hinter dem Spalt eine (nahezu) konstante Phasenlage zueinander aufweisen, und somit einzelne Wellen gleicher Wellenlänge jeweils kohärent sind. Bei der Verwendung von Lasern kann die spaltartige Blende vor dem Gitter weggelassen werden, da Laser aufgrund ihres besonderen Aufbaus bereits von sich aus kohärentes Licht erzeugen.
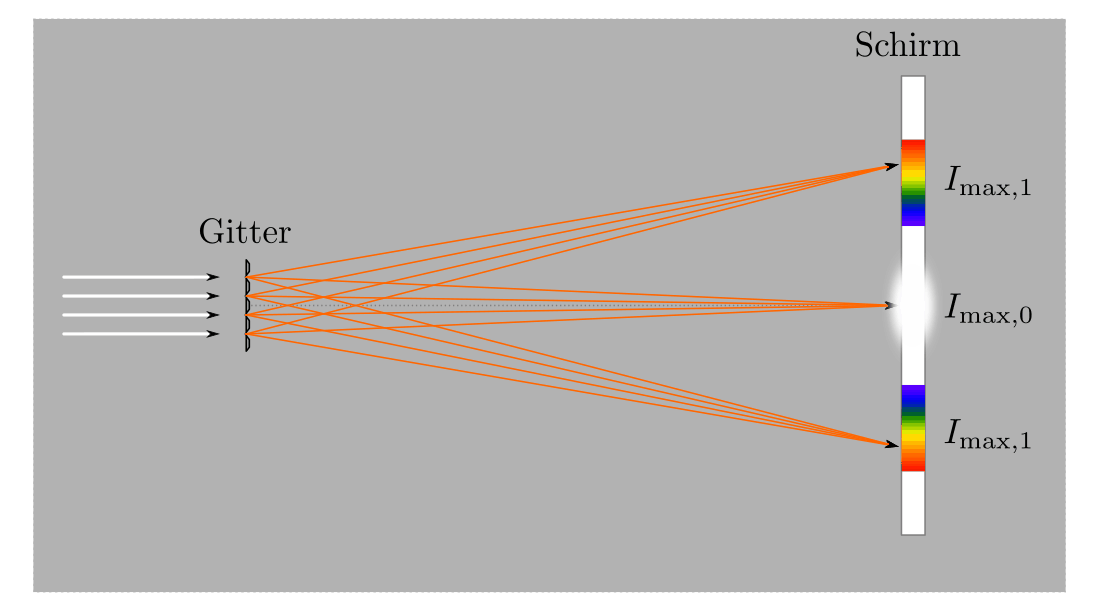
Verwendet man weißes Licht als Lichtquelle, das mehrere Farbanteile hat, so
fächern sich diese an den Stellen der maximalen Intensitäten auf dem Schirm zu
regenbogenartigen Spektren auf; sind manche Wellenlängen in der Lichtquelle
nicht enthalten, so bleiben die jeweiligen Stellen im Spektrum dunkel. Nach
Gleichung (3) ist die Ablenkung proportional zur
Wellenlänge 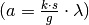 , blaues Licht wird
also weniger stark abgelenkt als rotes. Diese Eigenschaft wird beispielsweise
zur so genannten Spektralanalyse genutzt.
, blaues Licht wird
also weniger stark abgelenkt als rotes. Diese Eigenschaft wird beispielsweise
zur so genannten Spektralanalyse genutzt.
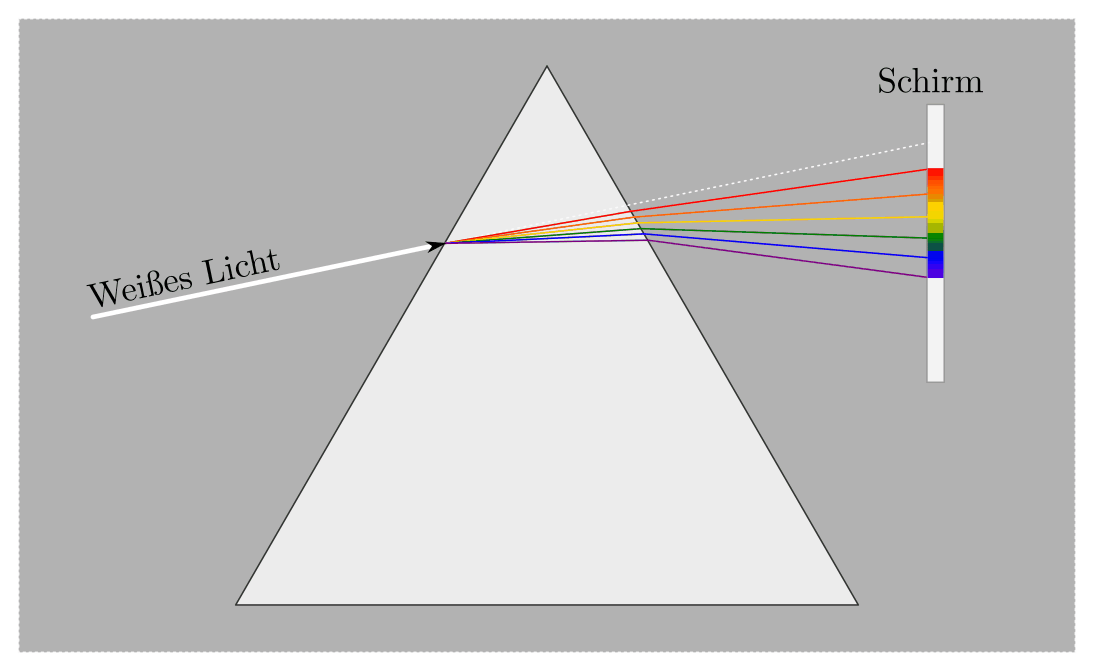
Lichtdispersion¶
Die Ausbreitungsgeschwindigkeit von Licht in einem optischen Medium ist nicht nur von dessen Brechungsindex, sondern auch von der Lichtfrequenz abhängig. Die unterschiedlichen Spektralanteile werden dadurch beispielsweise beim Durchgang durch ein Prisma unterschiedlich stark gebrochen, so dass sich mittels eines Prismas weißes Licht in seine Farbanteile aufteilen lässt.[3]
Technisch lässt sich dieses Prinzip der Spektralzerlegung auf zwei Arten nutzen:
- Bei einem „Monochromator“ wird anstelle eines Schirms eine Blende mit schmaler Öffnung angebracht. Dadurch wird nur ein schmaler Bereich (quasi eine einzelne Farbe) des Spektrums für weitere Versuchszwecke aus dem Lichtspektrum herausgefiltert.
- Bei einem „ref:Prismen-Spektrometer <Spektrometer>“ werden die Lichtanteile des Spektrums anhand einer Skala mit den Lichtanteilen bekannter Lichtquellen verglichen. Eine vergleichsweise einfache Kalibrierung wie bei einem optischen Gitter ist jedoch nicht möglich, da die Dispersion nicht linear mit der Lichtfrequenz bzw. der Wellenlänge zusammenhängt.
Bei einem Prisma, dessen Funktionsprinzip auf der Dispersion des Lichts beruht, wird blaues Licht stärker von der ursprünglichen Richtung abgelenkt als rotes; genau umgekehrt ist es bei einem optischen Gitter. Ein weiterer Unterschied zwischen diesen beiden Arten der Spektralerzeugung besteht darin, dass ein Prisma im Gegensatz zu einem optischen Gitter nur ein Spektrum erzeugt, das allerdings lichtintensiver ist als die einzelnen Gitterspektren.
Zur Spektralanalyse werden im Allgemeinen dennoch bevorzugt Gitter eingesetzt, zum einen aufgrund ihrer leichteren Kalibrierbarkeit, vor allem jedoch aufgrund der größeren Auffächerung bzw. der besseren „Auflösung“ beim Betrachten der einzelnen Spektrallinien.
Anmerkungen:
| [1] | Streng genommen ist dieses Modell, dass hinter einem sehr dünnen Spalt ein kreisförmiges Wellenzentrum entsteht, falsch. Tatsächlich gelangen durch jeden noch so dünnen Spalt mehrere Wellen parallel hindurch, die ebenfalls untereinander die Interferenz-Erscheinungen zeigen. Die Vorstellung ist dennoch ein hilfreiches Modell für die Erklärungen der Interferenzen am Doppelspalt und an optischen Gittern. |
| [2] | Auf diese Weise bestimmte Thomas Young im Jahr 1802 erstmals die Wellenlänge eines einfarbigen Lichtstrahls. |
| [3] | Das in Abbildung Lichtdispersion (Prisma) dargestellte Spektrum soll die
Aufgliederung der Farben schematisch verdeutlichen, ist dabei jedoch nicht
maßstabsgetreu gezeichnet. In Luft betragen die Wellenlängen für rotes
Licht ![780 \text{ bis } \unit[640]{nm}](../_images/math/b6c19e4a7cf624a221d911e4dbf59f36028c0c57.png) , für oranges Licht , für oranges Licht ![640
\text{ bis } \unit[600]{nm}](../_images/math/af1fd32877717adefcfd28c49e31ce8992d22a8d.png) , für gelbes Licht , für gelbes Licht ![600 \text{ bis }
\unit[580]{nm}](../_images/math/5af61c59f484ccf1e0278edccb88781f886a0f45.png) , für grünes Licht , für grünes Licht ![580 \text{ bis } \unit[495]{nm}](../_images/math/b501d8a3bcdaefe2d26c0323af28346bef018906.png) ,
für blaues Licht ,
für blaues Licht ![495 \text{ bis } \unit[440]{nm}](../_images/math/0ed5f3e683eb503a448de57342ca77edb2aa404d.png) und für violettes
Licht und für violettes
Licht ![440 \text{ bis } \unit[380]{nm}](../_images/math/0608eae3ceae194cbad755203eb57e504c2902d4.png) . . |