Photometrie¶
Die Farbwahrnehmung des Menschen¶
Die menschliche Farbwahrnehmung beruht auf speziellen Sinneszellen, die sich auf
der Netzhaut des Auges befinden. Insgesamt hat ein Mensch rund
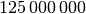 so genannte Zäpfchen, die für das Farb-Sehen sorgen, und
rund
so genannte Zäpfchen, die für das Farb-Sehen sorgen, und
rund 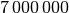 so genannte Stäbchen, die auf eine
Hell-Dunkel-Wahrnehmung ausgerichtet sind.
so genannte Stäbchen, die auf eine
Hell-Dunkel-Wahrnehmung ausgerichtet sind.
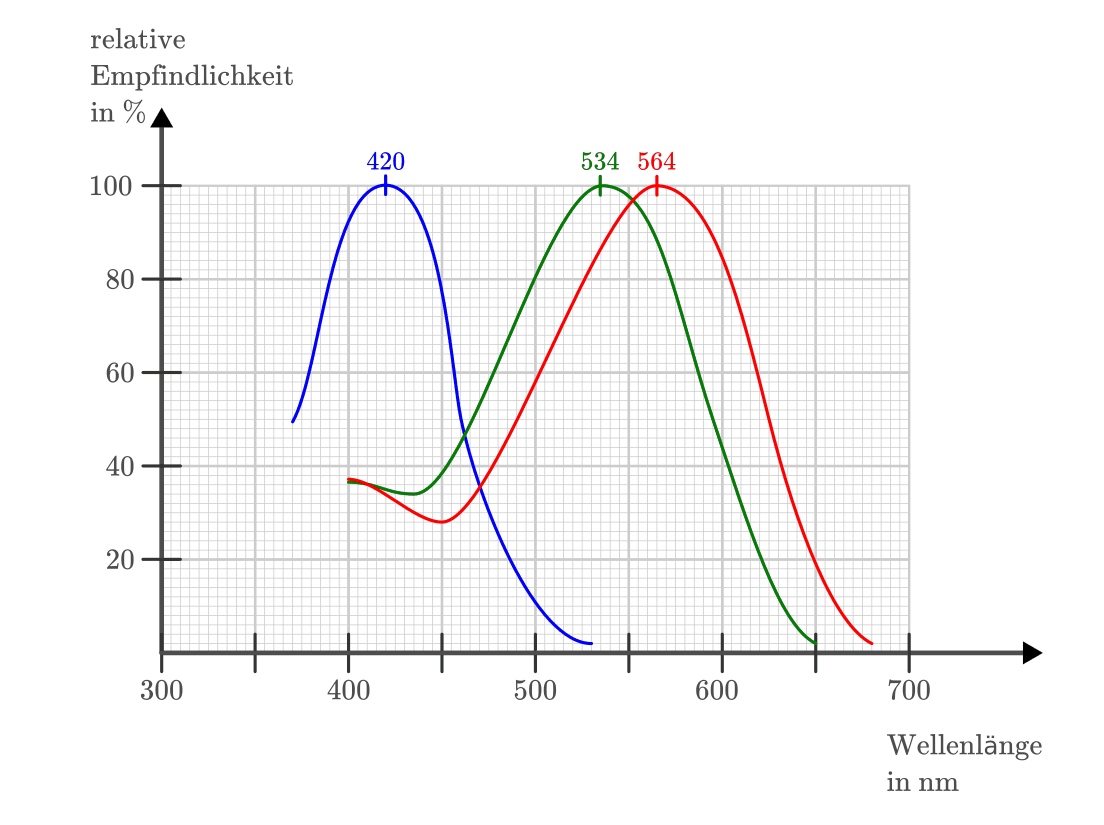
Bei den Zäpfchen gibt es drei verschiedene Typen, die ihre maximale
Empfindlichkeit im roten, grünen oder blauen Farbbereich haben. Jede derartige
Sinneszelle hat ihre maximale Empfindlichkeit bei einer bestimmten Wellenlänge,
bei größeren oder kleineren Wellenlängen nimmt die Empfindlichkeit stetig ab.
Insgesamt umfasst der menschliche Farbwahrnehmungsbereich ein
Wellenlängen-Spektrum von ca. ![\unit[380]{nm}](../_images/math/f74eb891904614de9c20f1895a79e28d12451ab7.png) bis
bis ![\unit[680]{nm}](../_images/math/09a08845adb8640f46ba01651cf0571cd9916a68.png) .
.
Additive und subtraktive Farbmischung
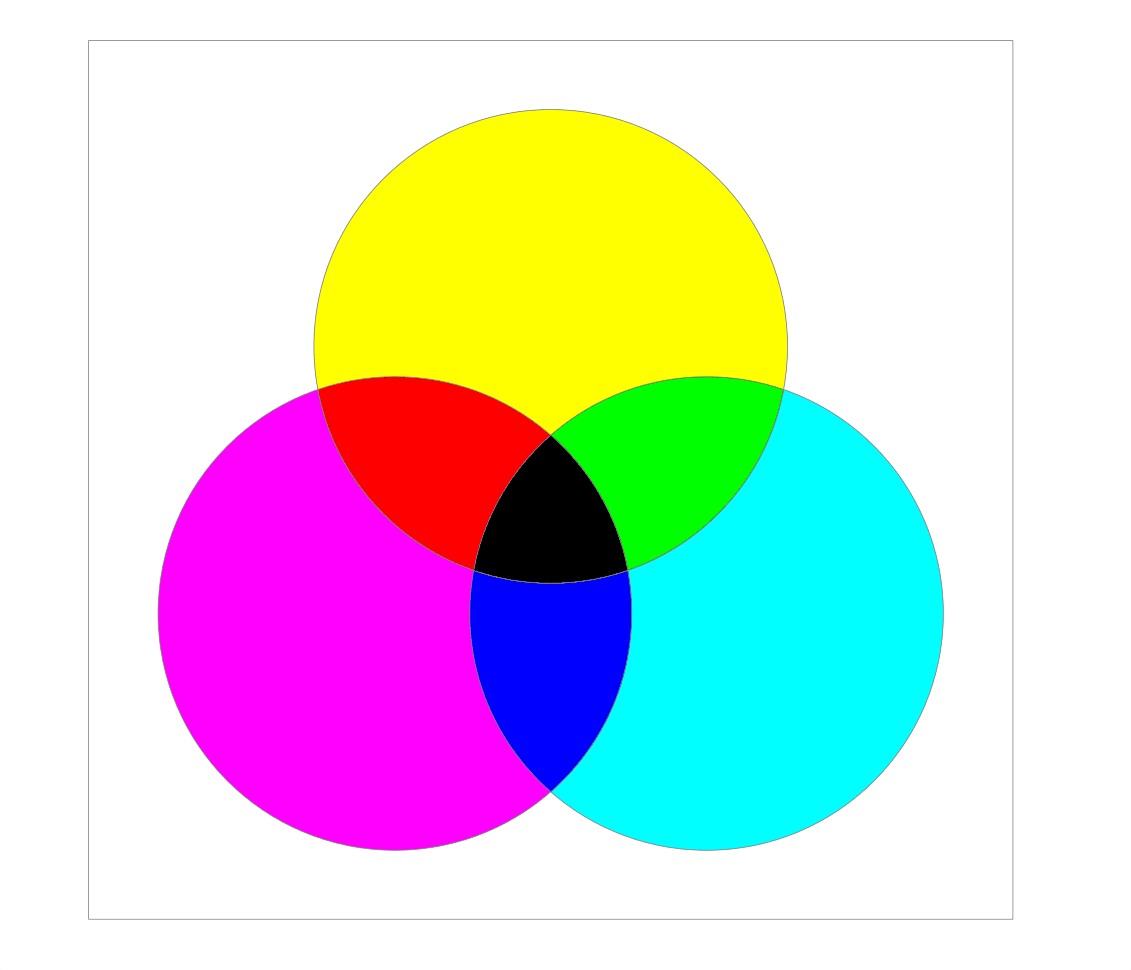
Das Gehirn kombiniert die einzelnen Sinneseindrücke für rotes, grünes und blaues Licht zu einer wahrgenommenen Gesamtfarbe. Nehmen wir alle drei Farben gleichzeitig wahr, so empfinden wir das Licht als weiß. Fehlt ein Farbanteil, so wird das Licht als Mischfarbe der beiden anderen Farben empfunden. Bei dieser „additiven“ Farbmischung sind die Grundfarben also Rot, Grün und Blau. Eine Mischung von Rot und Grün ergibt Gelb, eine Mischung von Rot und Blau ergibt Magenta, eine Mischung von Grün und Blau ergibt die Farbe Cyan.
Additive Farbmischung tritt beispielsweise bei mehrfarbigen Leuchtdioden (LEDs) auf. Lässt man eine Duo-LED gleichzeitig Rot und Grün leuchten, so ergibt sich ein gelblicher Farbton. Dieser Effekt wird nicht nur bei Computer-Displays verwendet, sondern tritt allgemein immer dann auf, wenn ein Material in einer Lichtquelle zum Leuchten angeregt wird. Beobachtet man ein so genanntes Emissions-Spektrum beispielsweise einer Leuchtstoffröhre, so erkennt man einzelne Farbanteile, die sich in der Summe zu einem weißlichen Licht addieren.
Neben der additiven Farbmischung kennt man vom Malen mit Wasserfarben auch die „subtraktive“ Farbmischung. Wird ein Farbanteil des weißen Lichts von einem Material absorbiert, so wird die Mischung der restlichen Farbanteile („Komplementärfarbe“) reflektiert und vom Auge wahrgenommen. Die Grundfarben dieser subtraktiven Farbmischung sind Gelb, Rot und Blau. Bei einer Mischung aus Gelb und Rot entsteht Orange, bei einer Mischung von Gelb und Blau entsteht Grün, und bei einer Mischung aus Rot und Blau entsteht Violett. Mischt man alle Grundfarben, so ergibt sich bei einer vollen Deckkraft die Farbe schwarz.
Subtraktive Farbmischung tritt ebenso auf, wenn weißes Licht durch ein transparentes, aber gefärbtes optisches Medium geht (beispielsweise eine Sonnenbrille). Beobachtet man ein sich so ergebendes Absorptionsspektrum, so hinterlassen die absorbierten Farben im Farbspektrums schwarze Linien (oder sogar schwarze Bereiche). Auf diese Weise kann beobachtet werden, welche Lichtanteile „herausgefiltert“ werden, was Rückschlüsse auf Materialeigenschaften oder chemische Substanzen zulässt.
Tag- und Nachtsehen
Die Zäpfchen für die rote, grüne und blaue Farbwahrnehmung sind nicht
gleichmäßig auf der Netzhaut verteilt. Während sich im zentralen Bereich der
Netzhaut überwiegend Zäpfchen für rotes und grünes Licht befinden, gibt es
im äußeren Bereich der Netzhaut mehr blaue Zäpfchen. Bei hoher Helligkeit ist
die Pupille als Blende eher geschlossen (klein), so dass das einfallende Licht
vorwiegend im zentralen Bereich der Netzhaut auftrifft. Bei dem so genannten
„Tagsehen“ hat das menschliche Auge die höchste Empfindlichkeit bei einer
Wellenlänge von ![\unit[555]{nm}](../_images/math/155da1b1512c3b8e57f975f3b76dd51564d6f42a.png) , also im grünen Farbbereich.
, also im grünen Farbbereich.
Bei zunehmender Dunkelheit vergrößert sich die Pupille, so dass mehr Licht in
das Auge gelangen kann. Dabei trifft ein größerer Lichtanteil auf die äußeren
Bereiche der Netzhaut. In diesem Fall tragen die am sensibelsten auf Licht
reagierenden Zäpfchen für blaues Licht stärker zur gesamten Lichtempfindlichkeit
des Auges bei. Die höchste Empfindlichkeit verschiebt sich bei dem so genannten
„Nachtsehen“ zu einer Wellenlänge von ![\unit[507]{nm}](../_images/math/d77eb5c845e4a8dfb9814ca912b2adf935f5c3e1.png) .
.
Lichttechnische Einheiten¶
In der Optik sind insgesamt acht lichttechnische Einheiten üblich. Aus historischen Gründen wird nach wie vor das Candela als Lichtstärke einer gewöhnlichen Kerze als Standard-Größe verwendet, auch wenn es aus heutiger Sicht sinnvoller erscheint, von der Strahlungsleistung einer Lichtquelle, gemessen in Watt, auszugehen. Je nachdem, ob die gesamte Strahlungsleistung einer Lichtquelle gemessen wird, oder nur derjenige Anteil, den sie als Lichtkegel in einen bestimmten Raumwinkel abstrahlt, sind die folgenden beiden Lichtgrößen grundlegend:
Der Strahlungsfluss
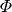 gibt an, welche Lichtleistung
gibt an, welche Lichtleistung 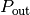 insgesamt von einer Lichtquelle ausgeht:
insgesamt von einer Lichtquelle ausgeht: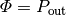
Die Einheit des Strahlungsflusses ist Watt
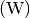 .
.
Die Strahlstärke
 gibt denjenigen Anteil
gibt denjenigen Anteil 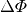 der
Lichtleistung an, die eine Lichtquelle in den Raumwinkel
der
Lichtleistung an, die eine Lichtquelle in den Raumwinkel 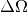 abstrahlt:
abstrahlt: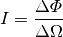
Die Einheit der Strahlstärke ist Watt je Steradiant
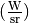 .
.
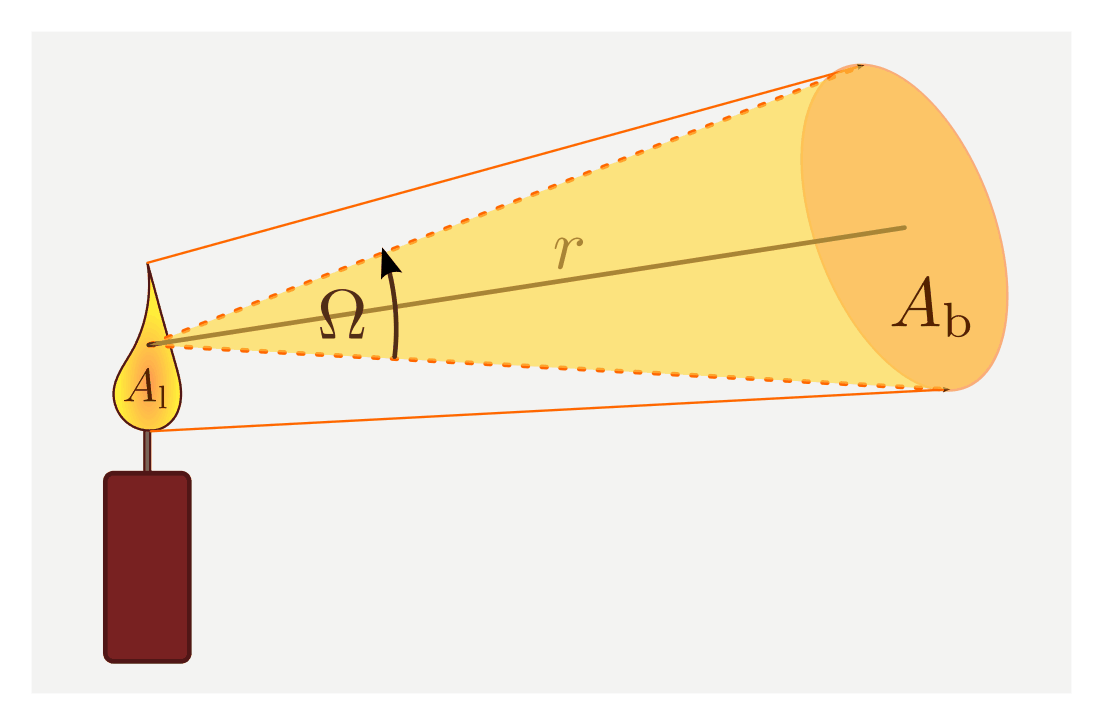
Beleuchtete und leuchtende Fläche als Bezugsgrößen bei der Definition der Bestrahlungsstärke und Strahldichte.
Diese zwei Größen werden als nächstes in Bezug zur beleuchteten beziehungsweise leuchtenden Fläche gesetzt. Damit ergeben sich folgende zwei weitere Einheiten:
Die Bestrahlungsstärke
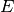 gibt an, wie viel Watt an Lichtleistung auf
eine beleuchteter Fläche
gibt an, wie viel Watt an Lichtleistung auf
eine beleuchteter Fläche 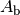 auftreffen:
auftreffen: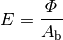
Die Einheit der Bestrahlungsstärke ist Watt je Quadratmeter
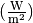 .
.
Die Strahldichte
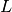 gibt an, wie viel Watt an Lichtleistung von einer
leuchtenden Fläche
gibt an, wie viel Watt an Lichtleistung von einer
leuchtenden Fläche 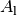 im Raumwinkel
im Raumwinkel 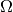 ausgehen:
ausgehen: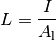
Die Einheit der Strahldichte ist Watt je Quadratmeter und Steradiant
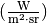 .
.
Die obigen Größen beziehen sich allgemein auf die abgestrahlte Leistung einer
Lichtquelle. Das menschliche Auge allerdings ist nicht für alle Lichtfrequenzen
(Farben) gleich empfindlich: Im grünen Farbbereich (![\lambda \approx
\unit[555]{nm}](../_images/math/8af3bba4cfc28f51fe7233af2bb7789e2d666079.png) ) ist das Auge beim Tagsehen am empfindlichsten.
) ist das Auge beim Tagsehen am empfindlichsten.
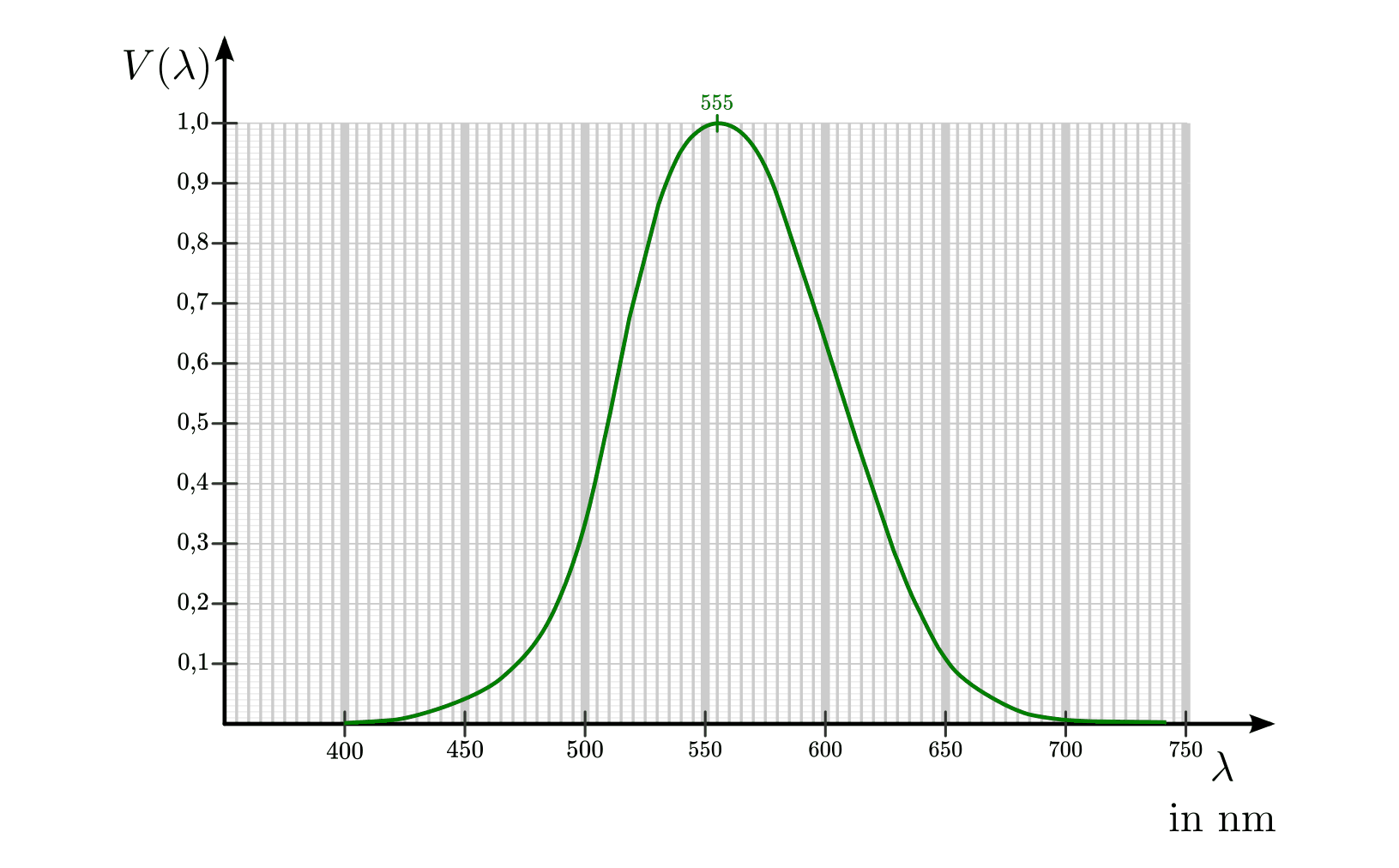
Um das Helligkeitsempfinden des menschlichen Auges zu berücksichtigen, werden
die vier obigen Größen jeweils mit einem von der Wellenlänge abhängigen Faktor
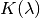 multipliziert, der die spektrale Empfindlichkeit des Auges
angibt:
multipliziert, der die spektrale Empfindlichkeit des Auges
angibt:
(1)¶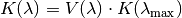
Der Gewichtungsfaktor 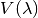 hat keine Einheit, sein Wert liegt
zwischen
hat keine Einheit, sein Wert liegt
zwischen 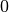 und
und 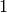 . Der zweite Faktor
. Der zweite Faktor 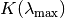 , auch photometrischen Äquivalent genannt, ist für das Tagsehen auf
, auch photometrischen Äquivalent genannt, ist für das Tagsehen auf
![K (\lambda_{\mathrm{max}}) = \unit[683]{\frac{lm}{W}}](../_images/math/ab60683940abe2622584f371b7efdd567f48355f.png) festgelegt. Dieser
Wert wurde so gewählt, weil bei dieser Strahlungsleistung eine monochromatische
Lichtquelle mit
festgelegt. Dieser
Wert wurde so gewählt, weil bei dieser Strahlungsleistung eine monochromatische
Lichtquelle mit ![\lambda = \unit[555]{nm}](../_images/math/bcd67ec096ab1e165a7c0b27e1c26aaf44055150.png) Wellenlänge als ebenso hell
empfunden wird wie eine Lichtquelle mit einer Lichtstärke von
Wellenlänge als ebenso hell
empfunden wird wie eine Lichtquelle mit einer Lichtstärke von
![\unit[1]{Candela}](../_images/math/031c6a635fe416145aad7c870c6f86296b74b0e0.png) .[1]
.[1]
Für den Lichtstrom
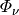 gilt:
gilt: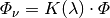
Die Einheit des Lichtstroms ist Lumen
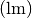 . Es gilt:
. Es gilt:![\unit[1]{lm} = \unit[1]{cd \cdot sr}](../_images/math/354565d4f750d84f5f174f62995d5a1b30e0c543.png)
Für die Lichtstärke
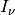 gilt:
gilt: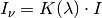
Die Einheit der Lichtstärke ist die SI-Basiseinheit Candela
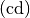 .
.
Für die Beleuchtungsstärke
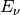 gilt:
gilt: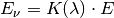
Die Einheit der Beleuchtungsstärke ist Lux
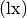 . Es gilt:
. Es gilt:![\unit[1]{lx} = \unit[1]{\frac{cd \cdot sr}{m^2}}](../_images/math/246162d34ecf58734af71fbe809a4b6155c2f696.png)
Für die Leuchtdichte
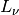 gilt:
gilt: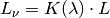
Die Einheit der Beleuchtungsstärke ist Nit
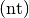 . Es gilt:
. Es gilt:![\unit[1]{nt} = \unit[1]{\frac{cd}{m^2}}](../_images/math/3bfab0ec2b77d46a1a54d7342e2d2bdedc18c647.png)
Funktionsprinzip von Spektrometern¶
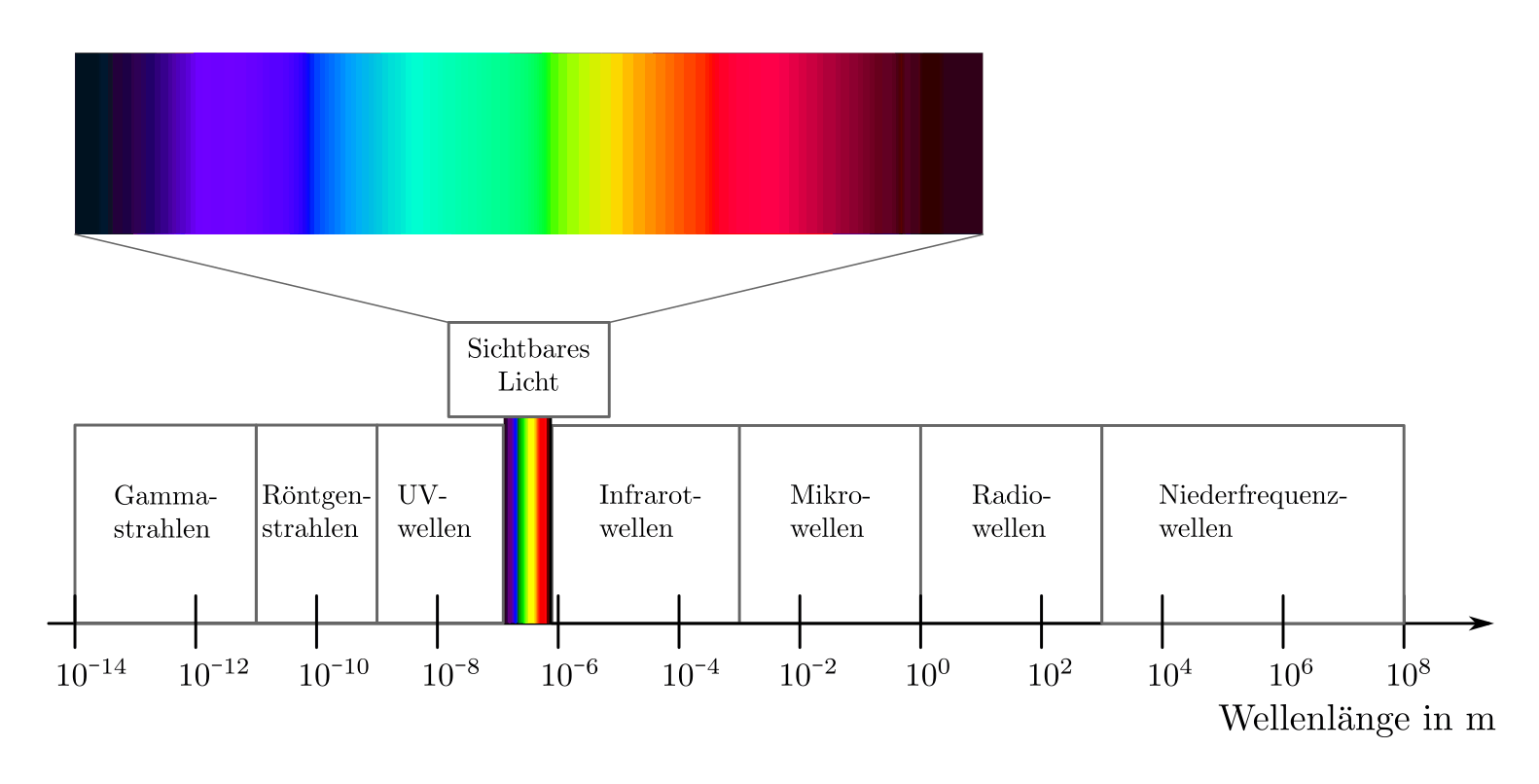
Das, was man üblicherweise als (farbiges) „Licht“ bezeichnet, ist nur ein kleiner Teil des Spektrums elektromagnetischer Strahlung. In der folgenden Abbildung ist dies schematisch dargestellt.
Sonnenlicht enthält Licht aus dem gesamten sichtbaren Farbspektrum, es erscheint uns daher, wie bereits oben beschrieben, als weiß. Trifft ein dünner Lichtstrahl weißen Lichts auf ein Prisma oder ein optisches Gitter, so wird er in seine Spektralfarben aufgefächert; das Licht erscheint als Regenbogen.
Mittels einer fein eingestellten Blende kann man damit gezielt Licht mit einer bestimmten Wellenlänge aus dem Spektrum auswählen. Man erhält somit eine einfarbige („monochromatische“) Lichtquelle, allerdings mit einstellbarer Wellenlänge. Strahlt man nun mit einer derartigen Lichtquelle auf eine Material-Probe (welche oftmals in gelöster Form vorliegt und daher in eine Glas-Küvette gegeben wird), so wird das Licht von dieser je nach Substanz der Probe unterschiedlich stark absorbiert. Misst man die Absorption der Probe bei verschiedenen Wellenlängen, so erhält man ein für die jeweilige Substanz charakteristischen Bild, also quasi einen „Fingerabdruck“ der Probe.
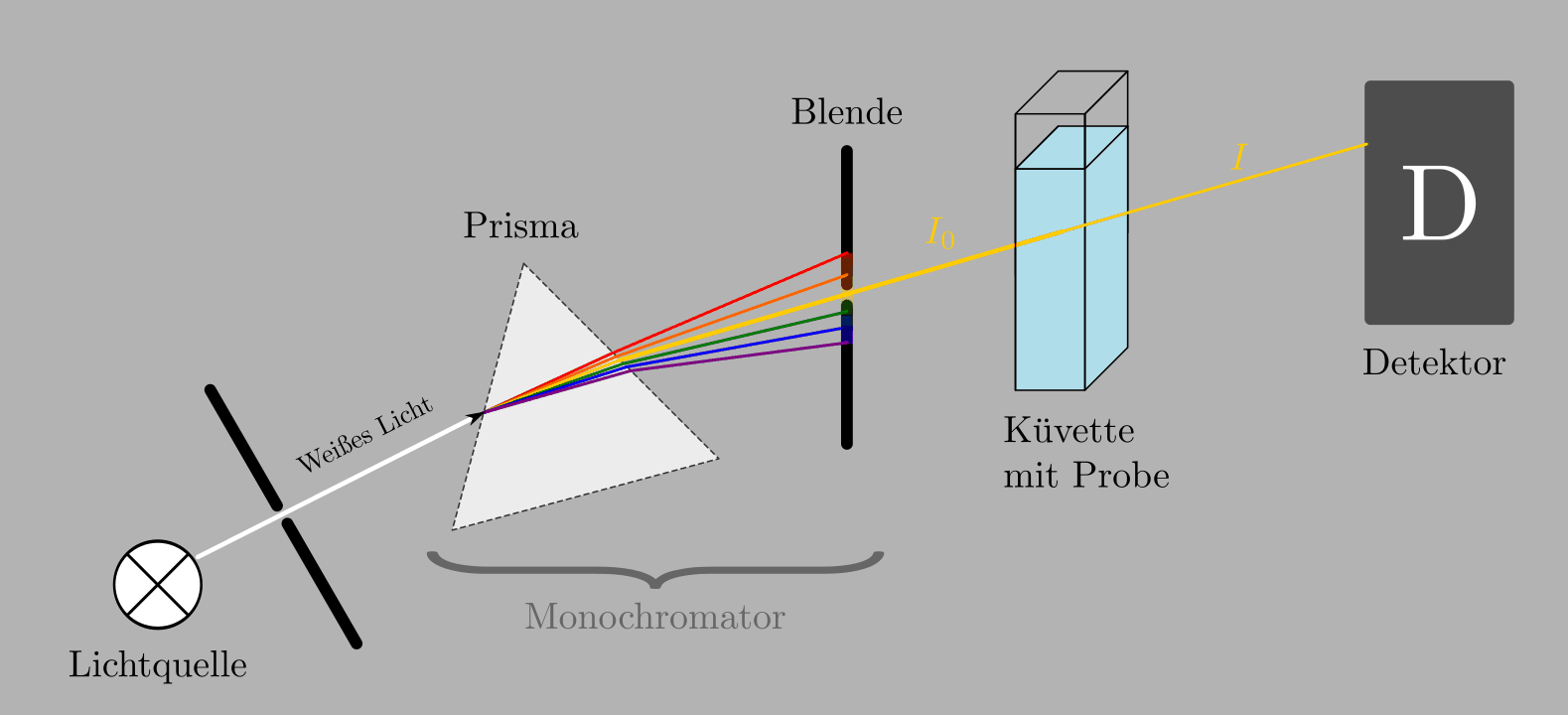
Ein Spektrometer, wie es heute zur Materialanalyse genutzt wird, besteht also im Wesentlichen aus vier Teilen:
Einer Lichtquelle, Monochromator, Probe und Detektor.
Eine Lichtquelle, in der Regel eine Halogenlampe, sendet weißes („polychromatisches“) Licht aus.
Ein Monochromator „zerlegt“ dieses Licht in monochromatisches Licht, also Strahlung einer bestimmten, einstellbaren Wellenlänge. Die Zerlegung kann entweder mittels eines Prismas oder mittels eines optischen Gitters erfolgen.
Ein Prisma erzeugt nur ein Spektrum und ermöglicht daher eine höhere Leuchtkraft, ist aber nur schwer kalibrierbar. Ein optisches Gitter fächert das Licht in eine Vielzahl von Einzel-Spektren auf, ist dafür jedoch aufgrund des bereits im Abschnitt Wellenoptik beschriebenen Zusammenhangs wesentlich einfacher kalibrierbar.
Mittels einer schmalen, verschiebbaren Blende kann gezielt eine Lichtfarbe beziehungsweise ein nur sehr schmaler Bereich von Wellenlängen selektiert werden.
Die Probe, häufig in einer Flüssigkeit gelöst, absorbiert einen Teil des Lichts. Während die die Lichtstärke des vom Monochromator ausgehenden Strahls noch
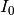 beträgt, verlässt der Strahl die Probe mit einer verringerten
Intensität
beträgt, verlässt der Strahl die Probe mit einer verringerten
Intensität  .
.Ein Detektor misst die durch die Probe gehende Intensität der Lichtstrahlung und leitet die gemessen Daten zur Auswertung an einen Computer weiter.
Das Lambert-Beersche Gesetz
Mit eine Spektrometer wird gemessen, wie stark Licht bei einer genau festgelegten Wellenlänge beim Durchgang durch eine mit einer flüssigen Probe gefüllten Küvette geschwächt wird. Beim Durchgang durch die Lösung wird das Licht exponentiell geschwächt, denn die in einer in einer bestimmten „Schichttiefe“ absorbierte Lichtmenge ist proportional zur dort vorhandenen Lichtmenge. Immer, wenn die Änderung einer Größe proportional zum jeweiligen Wert der Größe ist, lässt sich die Zu- beziehungsweise Abnahme der Größe mittels einer Exponentialfunktion beschreiben.
Der Zusammenhang zwischen der ursprünglichen Intensität 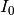 des Lichts
vor der Probe und der Intensität
des Lichts
vor der Probe und der Intensität  , die durch die Probe hindurchgeht
beziehungsweise den Schirm erreicht, kann also folgendermaßen beschrieben
werden:
, die durch die Probe hindurchgeht
beziehungsweise den Schirm erreicht, kann also folgendermaßen beschrieben
werden:
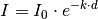
Hierbei bezeichnet 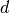 die Schichtdicke der Probe, also die (innere)
Breite der Küvette. Der Proportionalitätsfaktor
die Schichtdicke der Probe, also die (innere)
Breite der Küvette. Der Proportionalitätsfaktor 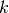 heißt
„Extinktionskoeffizient“ und hängt von der Art und Konzentration der der flüssigen
Probe sowie von der Wellenlänge des Lichts ab.
heißt
„Extinktionskoeffizient“ und hängt von der Art und Konzentration der der flüssigen
Probe sowie von der Wellenlänge des Lichts ab.
Die Schwächung („Extinktion“) des Lichts ergibt sich aus dem Quotienten von
 und
und 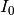 :
:
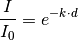
Bildet man auf beiden Seiten dieser Gleichung den Kehrwert, so erhält man die
Extinktion 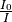 :
:
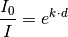
Um diese Gleichung nach dem Extinktionskooeffizienten 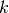 auflösen zu
können, müssen beide Seiten der Gleichung logarithmiert werden. Man erhält:
auflösen zu
können, müssen beide Seiten der Gleichung logarithmiert werden. Man erhält:
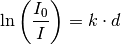
Üblicherweise wird in der Photometrie nicht mit dem natürlichen Logarithmus, sondern mit dem dekadischen gerechnet; für die Umrechnung gilt:
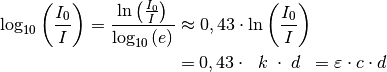
Hierbei bezeichnet man den Faktor  als molaren dekadischen
Extinktionskoeffizient der betreffenden gelösten Substanz für die verwendete
Wellenlänge; mit
als molaren dekadischen
Extinktionskoeffizient der betreffenden gelösten Substanz für die verwendete
Wellenlänge; mit  wird die molare Konzentration der gelösten Substanz
angegeben. Dieser Zusammenhang, dass die Konzentration des gelösten Stoffes
proportional zum Logarithmus der Extinktion
wird die molare Konzentration der gelösten Substanz
angegeben. Dieser Zusammenhang, dass die Konzentration des gelösten Stoffes
proportional zum Logarithmus der Extinktion 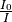 ist, wird nach
ihren Entdeckern Lambert-Beer’sches-Gesetz genannt.
ist, wird nach
ihren Entdeckern Lambert-Beer’sches-Gesetz genannt.
Spektralanalyse¶
Die Spektralanalyse ist, wie bereits erwähnt, ein wichtiges Verfahren zur Identifikation und/oder Konzentrationsbestimmung unbekannter Substanzen.
Kontinuierliche und diskrete Spektren
Emissions- und Absorptionsspektren
… to be continued …
Anmerkungen:
| [1] | Tatsächlich konnte auf diese Weise die zunächst sehr willkürliche
Einheit Candela („Helligkeit einer üblichen Kerze“) nachträglich präzise
festgelegt werden: Für das Nachtsehen ist |



![\unit[\frac{1}{683}]{\frac{W}{sr}}](../_images/math/a3474ab74a28abec8858f992fd232a616115c361.png) abgegeben wird.
abgegeben wird.![\lambda_{\mathrm{max}} = \unit[507]{nm}](../_images/math/7ce19aa2c54833794643cac26de1cd113cf39d33.png) und
und
![K (\lambda_{\mathrm{max}}) = \unit[1699]{\frac{lm}{W}}](../_images/math/9d29df3a580b4fc2435c110af9abc057e7a86ec6.png) .
.