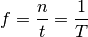Mechanische Schwingungen¶
Eine Schwingung entspricht allgemein einer zeitlich periodischen Änderung einer physikalischen Größe. Mechanische Schwingungen im Speziellen beschreiben Vorgänge, bei denen sich ein Körper regelmäßig um eine Gleichgewichtslage („Ruhelage“) bewegt.
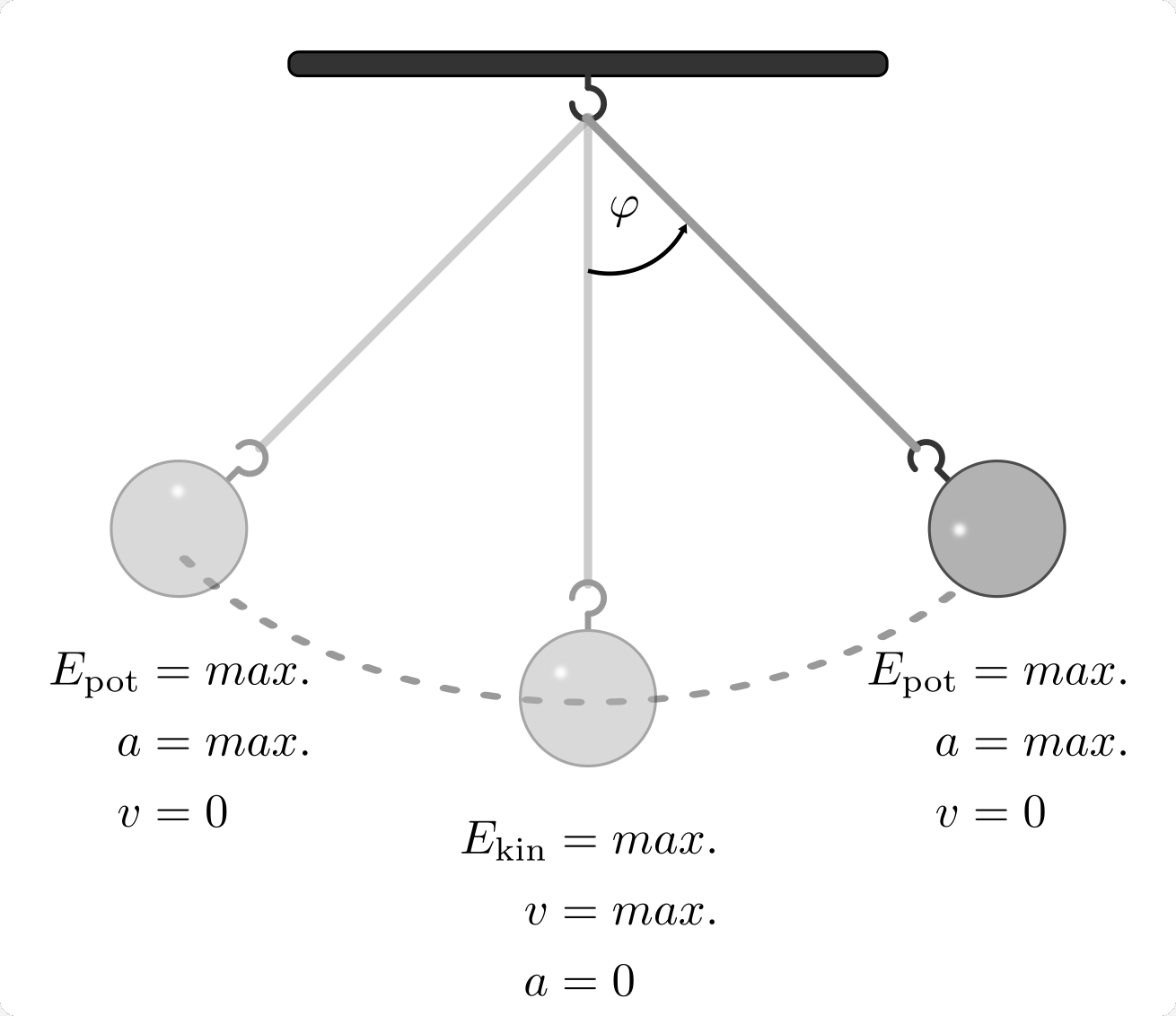
Bei jedem Durchlauf ändern sich dabei der Abstand von der Gleichgewichtslage
beziehungsweise der Auslenkwinkel 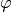 , die Beschleunigung
, die Beschleunigung
 , die Geschwindigkeit
, die Geschwindigkeit  und die damit verbundene Lage- und
Bewegungsenergie
und die damit verbundene Lage- und
Bewegungsenergie 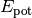 und
und 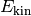 in
regelmäßiger Weise.
in
regelmäßiger Weise.
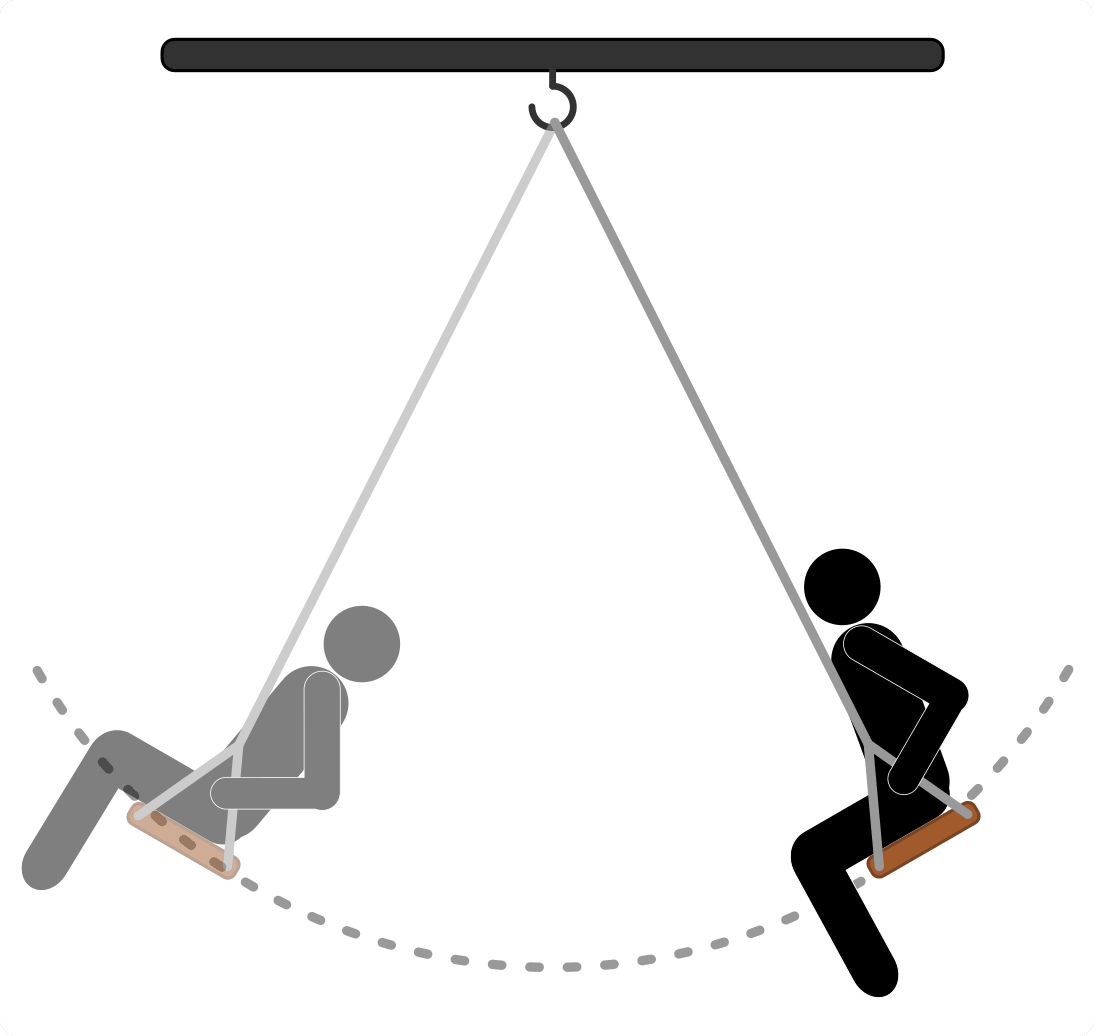
Schwingungen treten auf, wenn ein schwingungsfähiger Körper (auch „Schwinger“ oder „Oszillator“ genannt) durch Energiezufuhr aus der Gleichgewichtslage („Ruhelage“) ausgelenkt wird. Zusätzlich ist stets eine zur Ruhelage rücktreibende Kraft vorhanden, die den schwingenden Körper daran hindert die Bahn zu verlassen.
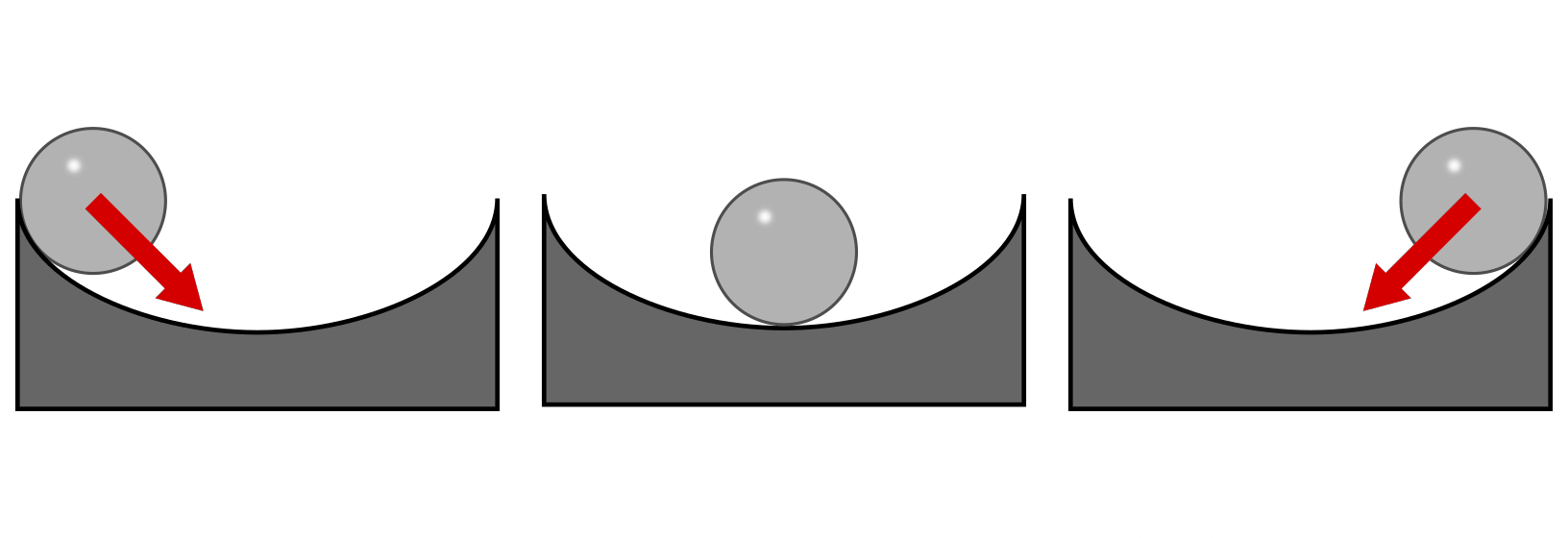
Eine Kugel in einer „Half-Pipe“ erfährt bei Auslenkung eine zur Gleichgewichtslage rückwirkende Kraft.
Ohne wirkende Reibungskräfte wiederholt sich der Schwingungsvorgang (theoretisch) unendlich oft.
Amplitude, Schwingungsdauer und Frequenz¶
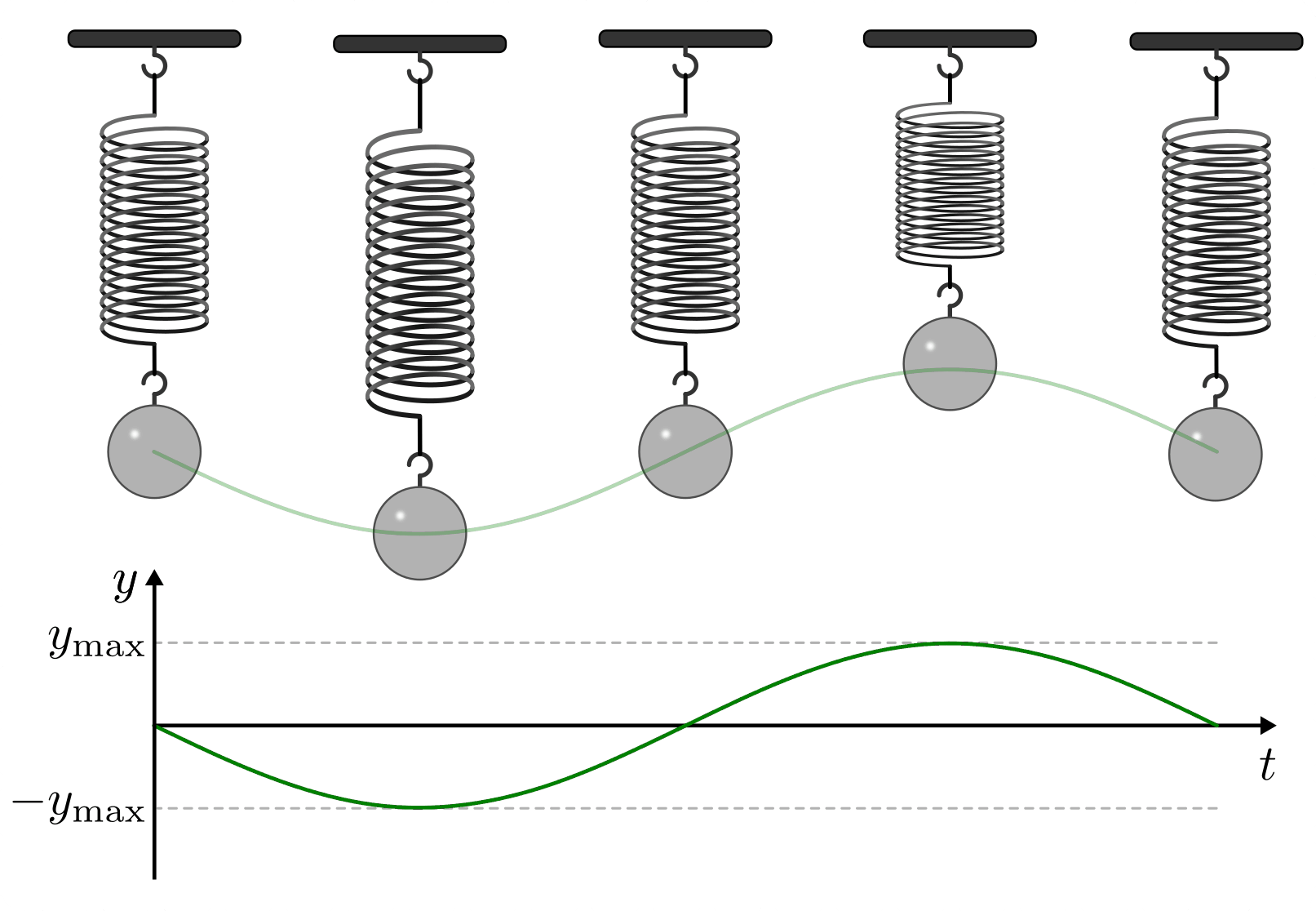
Der zeitliche Verlauf der Auslenkung eines schwingenden Körpers kann mittels eines Weg-Zeit-Diagramms dargestellt werden. Dabei ergibt sich ein für den jeweiligen Schwinger charakteristischer, periodischer Kurvenverlauf.
Hat die Weg-Zeit-Funktion einer Schwingung die Form einer Sinus-Funktion, so bezeichnet man die Schwingung als harmonisch; andernfalls nennt man sie anharmonisch.
Jede Schwingung kann durch folgende Größen beschrieben werden:
- Die Auslenkung
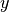 (auch „Elongation“ genannt) gibt den momentanen
Abstand des schwingenden Körpers von der Gleichgewichtslage an. Die maximale
Auslenkung
(auch „Elongation“ genannt) gibt den momentanen
Abstand des schwingenden Körpers von der Gleichgewichtslage an. Die maximale
Auslenkung 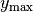 wird als Amplitude bezeichnet.
wird als Amplitude bezeichnet.
- Die Schwingungsdauer
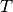 gibt an, wie viel Zeit der schwingende Körper
für eine vollständige Hin- und Herbewegung („Periode“) benötigt.
gibt an, wie viel Zeit der schwingende Körper
für eine vollständige Hin- und Herbewegung („Periode“) benötigt.
Anstelle der Schwingungsdauer wird häufig auch mit der Frequenz 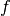 einer
Schwingung gerechnet. Sie gibt die Anzahl an Schwingungen
einer
Schwingung gerechnet. Sie gibt die Anzahl an Schwingungen  an, die ein
Körper in einer bestimmten Zeit
an, die ein
Körper in einer bestimmten Zeit  ausführt. Für einen einzigen
Schwingungsvorgang
ausführt. Für einen einzigen
Schwingungsvorgang 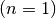 benötigt ein schwingender Körper genau die
Zeitdauer
benötigt ein schwingender Körper genau die
Zeitdauer 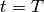 . Somit gilt:
. Somit gilt:
(1)¶
Frequenzen werden in der nach Heinrich Hertz benannten Einheit „Hertz“
![(\unit[]{Hz})](../../_images/math/3ee5803d0ec3af098dee5a7566482c7f1302ce4a.png) angegeben. Eine Frequenz von
angegeben. Eine Frequenz von ![\unit[1]{Hz} =
\unit[]{\frac{1}{s} }](../../_images/math/0d9f7409915274bf3efe6d54d8eb2eb79fe0ae8b.png) bedeutet, dass in einer Sekunde genau ein
Schwingungsvorgang stattfindet.
bedeutet, dass in einer Sekunde genau ein
Schwingungsvorgang stattfindet.
Gedämpfte Schwingungen¶
Mechanische Schwingungen setzen sich, falls keine Reibungskräfte wirken, ungedämpft fort; ihre Amplitude bleibt also zeitlich konstant. Reale Schwingungen hingegen kommen, sofern ihnen nicht regelmäßig Energie zugeführt wird, nach einer gewissen Zeit zum Erliegen. Einen Vorgang, bei denen die Amplitude stetig abnimmt, bezeichnet man als gedämpfte Schwingung.
Ist die Dämpfung abhängig von der Geschwindigkeit, was beispielsweise bei
Luftreibung der Fall ist, so nimmt die anfängliche Amplitude 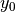 exponentiell mit der Zeit ab. Für die Amplitude
exponentiell mit der Zeit ab. Für die Amplitude 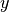 zum Zeitpunkt
zum Zeitpunkt
 gilt dabei in Abhängigkeit vom Dämpfungsgrad
gilt dabei in Abhängigkeit vom Dämpfungsgrad 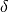 :
:
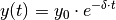
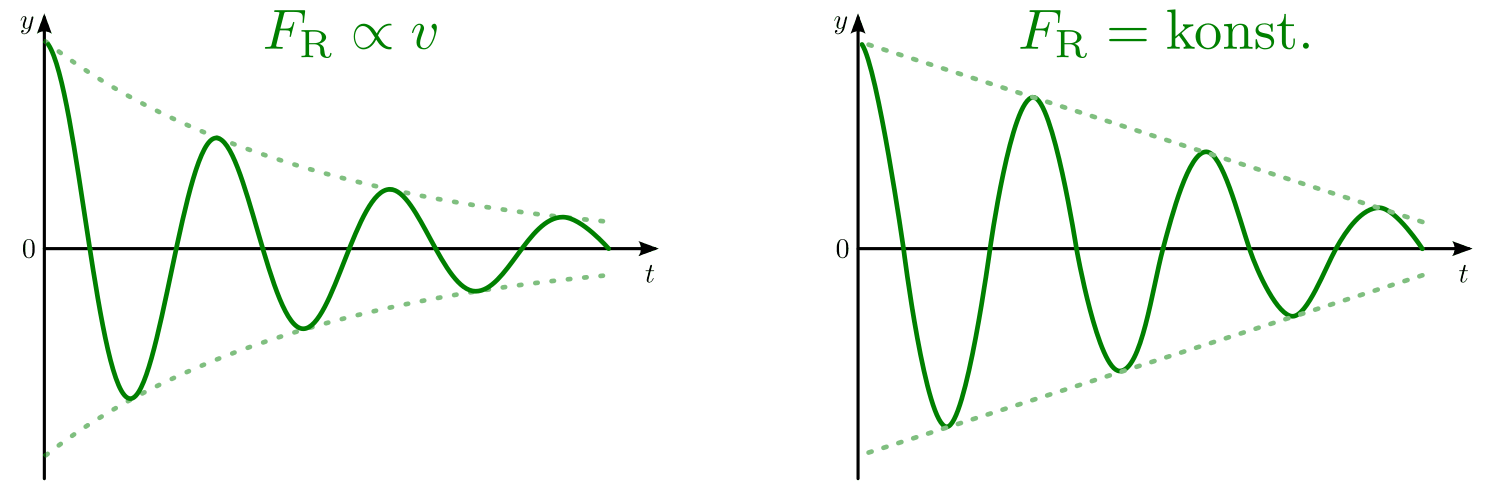
Zeitlicher Verlauf einer Schwingung mit geschwindigkeitsabhängiger beziehungsweise konstanter Dämpfung.
Ebenfalls möglich ist eine konstante dämpfende Kraft, beispielsweise infolge von (Gleit-)Reibung. In diesem Fall ist die Differenz zweier benachbarter Amplituden konstant, die Amplitude der Schwingung nimmt somit linear ab.
Jede Dämpfung bewirkt bei Schwingungen eine Verkleinerung der Frequenz beziehungsweise eine Vergrößerung der Schwingungsdauer.
Erzwungene Schwingungen und Resonanz¶
Wird ein schwingendes System einmalig angeregt und dann sich selbst überlassen,
so führt es Schwingungen mit seiner Eigenfrequenz 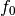 aus. Wird die
Energie jedoch über einen längeren Zeitraum hinweg periodisch zugeführt, so
führt das schwingende System – nach einer kurzen Übergangszeit – so genannte
„erzwungene“ Schwingungen mit der Frequenz
aus. Wird die
Energie jedoch über einen längeren Zeitraum hinweg periodisch zugeführt, so
führt das schwingende System – nach einer kurzen Übergangszeit – so genannte
„erzwungene“ Schwingungen mit der Frequenz 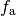 des anregenden
Systems aus.
des anregenden
Systems aus.
Die Amplitude der angeregten Schwingungen ist von der Erregerfrequenz
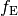 abhängig. Stimmt diese mit der Eigenfrequenz
abhängig. Stimmt diese mit der Eigenfrequenz 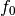 des angeregten Systems überein, so spricht man von Resonanz. Die Amplitude
des angeregten Systems überein, so spricht man von Resonanz. Die Amplitude
 des angeregten Systems wird in diesem Fall maximal.
des angeregten Systems wird in diesem Fall maximal.
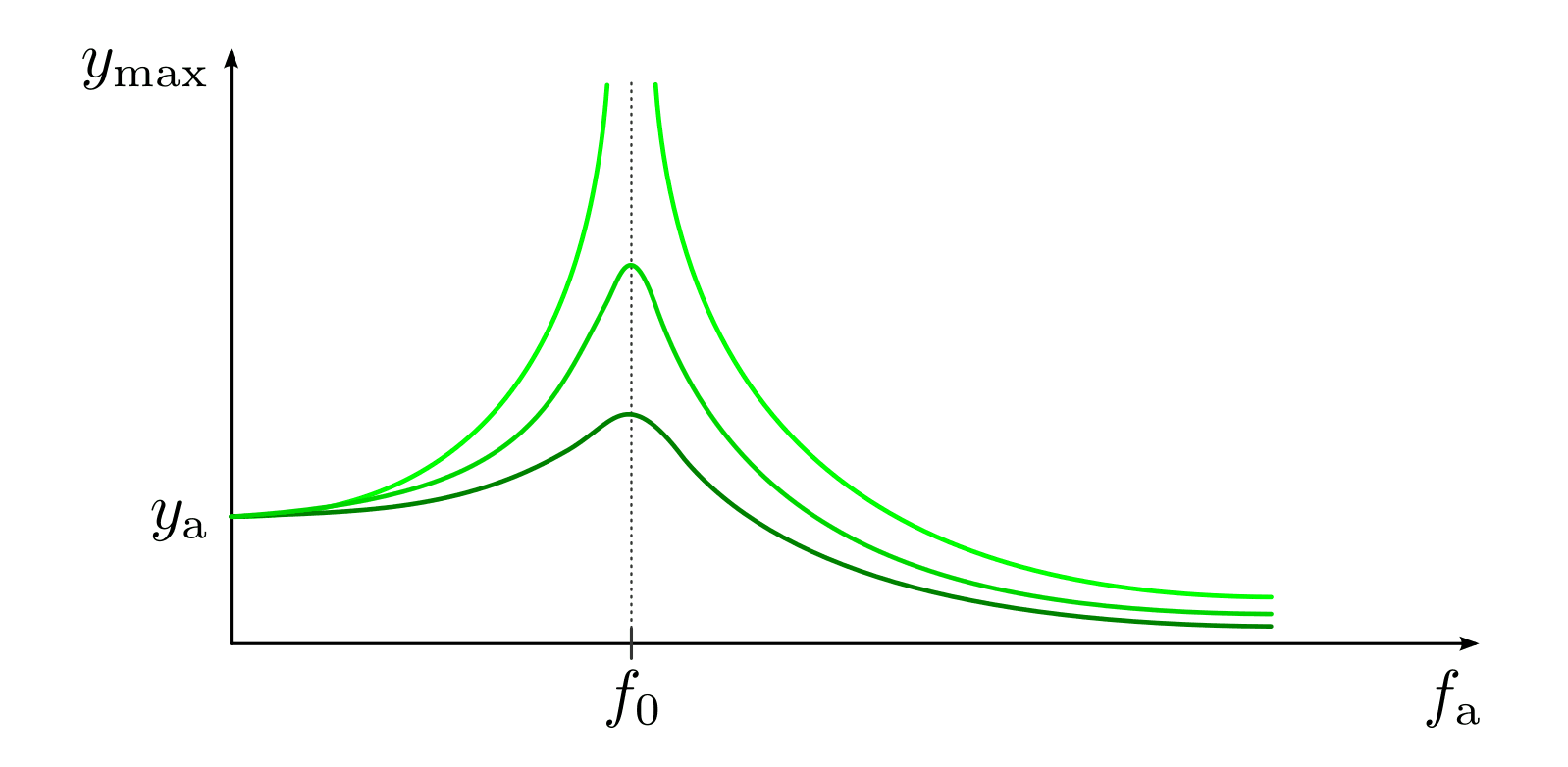
Amplitude einer erzwungenen Schwingung in Abhängigkeit von der anregenden Frequenz. Hellere Kurven kennzeichnen eine schwächere Dämpfung.
Trägt man die Amplitude  in Abhängigkeit der Erregerfrequenz auf, so
erhält man eine so genannte „Resonanzkurve“. Das Resonanzmaximum ist umso
ausgeprägter (schmäler und höher), je geringer der Dämpfungsgrad ist. Bei sehr
schwachen Dämpfungen kann sich das angeregte System also zu sehr großen
Amplituden „aufschaukeln“, was im technischen Bereich teilweise absichtlich
genutzt, teilweise aber auch gezielt vermieden wird:
in Abhängigkeit der Erregerfrequenz auf, so
erhält man eine so genannte „Resonanzkurve“. Das Resonanzmaximum ist umso
ausgeprägter (schmäler und höher), je geringer der Dämpfungsgrad ist. Bei sehr
schwachen Dämpfungen kann sich das angeregte System also zu sehr großen
Amplituden „aufschaukeln“, was im technischen Bereich teilweise absichtlich
genutzt, teilweise aber auch gezielt vermieden wird:
- Resonanzeffekte werden beispielsweise zur Entfernung von Nierensteinen genutzt; dabei werden diese mit hoch intensivem Ultraschall unterschiedlicher Frequenz behandelt. Die spröden Steine können dabei, wenn jeweils die richtige Frequenz getroffen wird, zu so großen Schwingungen angeregt werden, dass sie in kleinere, für den Körper nicht mehr gefährliche Teilstücke zerfallen.
- Resonanzeffekte werden möglichst immer vermieden, wenn damit mechanische Belastungen verbunden sind. Beispielsweise durchlaufen Wäscheschleudern am Anfang und am Ende eines Schleudergangs kontinuierlich eine Vielzahl an unterschiedlichen Frequenzen (Drehzahlen). Bei ungünstigen Frequenzwerten kommt es zu großen Schwingungsamplituden des an Schraubenfedern aufgehängten Schleuderbehälters. Durch Ausgleichsgewichte versucht man in diesem Fall die Unwucht und das damit verbundene hörbare „Klappern“ gering zu halten.
Bei Drehbewegungen wird die Resonanzfrequenz als kritische Drehzahl bezeichnet. Eine besondere Bedeutung haben Resonanzeffekt zudem in der Akustik, beispielsweise wenn mitschwingende Klangkörper eine Verstärkung eines bestimmten Tons bewirken sollen.