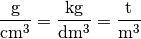Körpereigenschaften¶
Alle physikalischen Körper, also räumlich begrenzte Materieformen, bestehen aus Stoffen und besitzen gemeinsame physikalische Eigenschaften. Umgangssprachlich bezeichnet man physikalische beziehungsweise geometrische Körper häufiger als „Objekte“.
Masse¶
Jedes physikalische Objekt besteht aus Materie; jeder Materie-Baustein wiederum
„wiegt“ etwas, so dass jedes physikalische Objekt auch stets eine gewisse Masse
 als charakteristische Eigenschaft aufweist.
als charakteristische Eigenschaft aufweist.
Einheit:
Die Masse eines Objekts wird meist in Kilogramm
angegeben. Weitere gebräuchliche Einheiten sind die Tonne
und das Gramm
.
Die Masse  eines Objekts kann man an seiner Schwere beziehungsweise an
seiner Trägheit erkennen:
eines Objekts kann man an seiner Schwere beziehungsweise an
seiner Trägheit erkennen:
- Die Eigenschaft „Schwere“ gibt an, wie sehr ein Objekt in der Lage ist, sich selbst oder einen anderen Gegenstand im Gravitationsfeld eines Planeten zu beschleunigen. Als anschauliches Beispiel kann man an die „Gewichte“ einer Kuckucksuhr denken, die beim Herabsinken in der Lage sind, die Zeiger der Uhr anzutreiben.[1]
- Die Eigenschaft „Trägheit“ gibt an, wie sehr sich ein Objekt einer von außen einwirkenden Kraft widersetzt; man kann die „Trägheit“ eines Objekts somit als „Widerstand gegen Beschleunigung“ auffassen.
Im Rahmen seiner Relativitätstheorie konnte Albert Einstein zeigen, dass beide Eigenschaften stets im gleichen Maß vorhanden sind; es muss somit nicht explizit zwischen schwerer und träger Masse unterschieden werden.
Volumen¶
Jedes Objekt besitzt ein Volumen  , also eine räumliche Ausdehnung.
, also eine räumliche Ausdehnung.
Einheit:
Das Volumen
eines Objekts wird meist in Kubikmeter
angegeben. Weitere gebräuchliche Einheiten sind der Liter
und der Kubik-Zentimeter
:
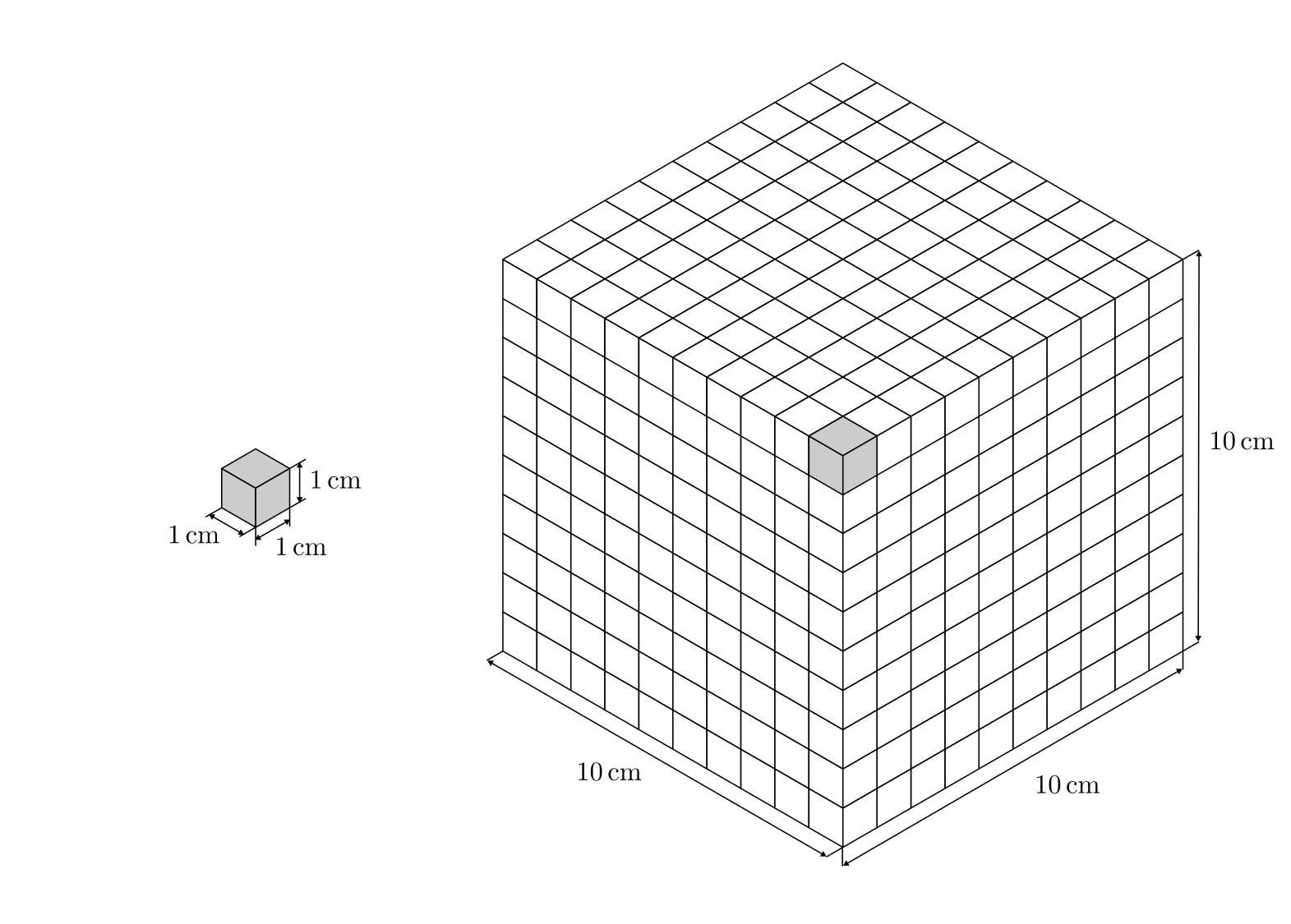
Ein Liter entspricht einem Kubik-Dezimeter, also einem Würfel von
![\unit[10]{cm} \times \unit[10]{cm} \times \unit[10]{cm}](../_images/math/4fdc034192d58fc21f0810cc39fce005ee180d0e.png) Kantenlänge.
Kantenlänge.
Zur Bestimmung des Volumens eines Objekts können folgende Methoden angewendet werden:
- Das Volumen eines festen, regelmäßig geformten Objekts kann durch geometrische Berechnung bestimmt werden. Dazu müssen die charakteristischen Längen der jeweiligen Form gemessen werden.
- Das Volumen eines festen, unregelmäßig geformten Objekts kann durch Flüssigkeitsverdrängung ermittelt werden.
- Das Volumen von Flüssigkeiten kann mit Messzylindern gemessen werden
- Gase verteilen sich gleichmäßig in dem zur Verfügung stehenden Raum. Das Volumen eines Gases kann daher bestimmt werden, indem das Volumen des vom Gas ausgefüllten Raumes gemessen wird.
Dichte¶
Die Dichte 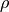 eines Gegenstands gibt an, welche Masse
eines Gegenstands gibt an, welche Masse  er bei
einem bestimmten Volumen
er bei
einem bestimmten Volumen  besitzt.
besitzt.
Definition:
Die Dichte
eines Objekts ist gleich dem Verhältnis aus seiner Masse
und seinem Volumen
:
(1)¶
Einheit:
Verwendet man Standard-Einheiten, so ergibt sich als Einheit für die Dichte Kilogramm je Kubikmeter
. Eine weitere gebräuchliche Einheit ist Gramm je Kubik-Zentimeter
:
Folgende Dichte-Einheiten können als gleichwertig verwendet werden:
Experimentell kann die Dichte eines Festkörpers bestimmt werden, indem man seine Masse mit Hilfe einer Waage bestimmt und sein Volumen durch Eintauchen in eine Flüssigkeit ermittelt. Nach dem Archimedischen Prinzip verdrängt jeder Gegenstand beim Eintauchen ebenso viel Flüssigkeit, wie er selbst an Volumen hat. Teilt man den Wert der Masse durch den Wert des Volumen, so erhält man die Dichte des Objekts.
| Stoff | Dichte in 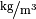 |
| Aluminium | 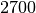 |
| Blei | 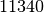 |
| Eis | 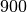 |
| Glas | 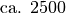 |
| Gold | 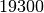 |
| Hartgummi | 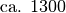 |
| Holz | 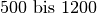 |
| Kork | 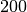 |
| Kupfer | 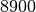 |
| Schaumstoff | 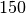 |
| Silber | 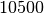 |
| Stahl | 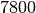 |
Die Dichte einer Flüssigkeit kann am einfachsten mit einem Aräometer gemessen werden: Je kleiner die Dichte der Flüssigkeit ist, desto weiter taucht das Aräometer in die Flüssigkeit ein. An der Skala des eintauchenden Aräometers kann die Dichte der Flüssigkeit somit direkt abgelesen werden.
| Stoff | Dichte in 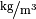 |
| Ethanol | 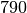 |
| Glycerin | 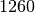 |
| Leichtbenzin | 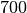 |
| Petroleum | 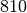 |
| Quecksilber | 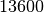 |
| Schmieröl | 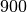 |
| Schwefelsäure | 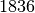 |
Wasser (bei ![\unit[4]{\degree C}](../_images/math/eed4ef41d7331125df384be9e18fd591c56a1acf.png) ) ) |
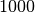 |
Die Dichte von Gasen hängt stark vom Druck und von der Temperatur ab. Um die Dichten
verschiedener Gase dennoch vergleichen zu können, werden die entsprechenden
Werte für Normalbedingungen, also Druck ![p = \unit[1]{bar}](../_images/math/c32e42b677c5d7dea7fc0ae9aab58f0244fe8aa5.png) und
und ![T =
\unit[0]{\degree C}](../_images/math/f7015137a6f66b1095fc30b5b88d127b585572af.png) , angegeben.
, angegeben.
Stoff (bei ![\unit[0]{\degree C }](../_images/math/e5d0d91bddea192b9039d5bf324be1816553890b.png) ) ) |
Dichte in 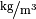 |
| Chlor | 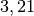 |
| Helium | 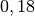 |
| Kohlenstoffdioxid | 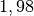 |
| Luft | 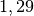 |
| Methan | 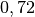 |
| Wasserstoff | 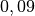 |
| Xenon | 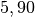 |
Durchschnittliche Dichte
Besteht ein Gegenstand aus mehr als einem Material, so setzt sich seine durchschnittliche Dichte aus den jeweiligen Massen- und Volumenanteilen zusammen:
![m_{\mathrm{ges}} &= m_1 + m_2 + \ldots \\
\rho_{\mathrm{ges}} \cdot V_{\mathrm{ges}} &= \rho_1 \cdot V_1 + \rho_2
\cdot V_2 + \ldots \\[6pt]](../_images/math/7aedf67f6b3297075689e544a6568af7a494e201.png)
Teilt man beide Seiten der Gleichung durch 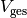 , so erhält
man für die durchschnittliche Dichte
, so erhält
man für die durchschnittliche Dichte 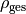 des Objekts:
des Objekts:
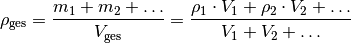
Da die Masse von Gasen gegenüber der von Festkörpern meist vernachlässigbar klein ist, kann die obige Formel beispielsweise genutzt werden, um den „Luftanteil“ eines porösen Gegenstands zu bestimmen.
Aggregatzustand¶
Da Objekte aus chemischen Stoffen bestehen und diese im festen, flüssigen und gasförmigen Aggregatzustand auftreten können, unterscheidet man entsprechend auch zwischen Festkörpern, Flüssigkeiten und Gasen.
Je nach Aggregatzustand zeigen Objekte ein unterschiedliches Volumen- und Formverhalten:
- Im festen Zustand sind die Atome einer Substanz in Kristallgittern oder Makro-Molekülen fest an ihre Plätze gebunden und können nur Schwingungen um ihre jeweilige Position ausführen.
- Im flüssigen Zustand können sich die einzelnen Atome beziehungsweise Moleküle innerhalb der Flüssigkeit frei bewegen. Der Austritt aus der Flüssigkeit wird jedoch durch zwischenmolekulare Kräfte stark erschwert.
- Im gasförmigen Zustand spielen zwischenmolekulare Kräfte so gut wie keine Rolle; die Atome beziehungsweise Moleküle können sich frei bewegen.
| Aggregatzustand | Fest | Flüssig | Gasförmig |
| Typisches Beispiel | Metall | Wasser | Luft |
| Volumen | Bestimmt | Bestimmt | Angepasst an Gefäßvolumen |
| Form | Bestimmt | Bestimmt | Angepasst an Gefäßform |
| Abstand zwischen Teilchen | Klein | Klein | Sehr groß |
| Verschiebbarkeit der Teilchen | Klein | Groß | Sehr groß |
| Kompressibilität | Sehr gering | Sehr gering | Sehr groß |
In welchem Aggregatzustand ein Material vorliegt, hängt vom Druck und von der Temperatur ab; im Abschnitt Phasenübergänge wird hierauf näher eingegangen.
Anmerkungen:
| [1] | „Gewicht“ und „Schwere“ sind nahezu gleichwertige Begriffe:
Die Unterscheidung zwischen „Schwere“ und „Gewicht“ ist somit vor allem allem sprachlicher Natur; beide Begriffe betonen, dass mit dem Vorhandensein von Masse stets auch Gravitationskräfte vorhanden sind. |
Hinweis
Zu diesem Abschnitt gibt es Experimente und Übungsaufgaben.

![\unit[1]{t} &= \unit[1000]{kg} \\
\unit[1]{kg} &= \unit[1000]{g}](../_images/math/ebecafd10e891d492ad53bbb23e9f2e9a0475fde.png)
![\unit[1]{m^3} &= \unit[10 \times 10 \times 10]{dm^3} = \unit[1000]{l} \\
\unit[1]{l} &= \unit[10 \times 10 \times 10]{cm^3} = \unit[1000]{cm^3}](../_images/math/4b09fe3cd7ef0fd6ef820417d352ce3467ab597f.png)
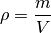
![\unit[1]{\frac{g}{cm^3} } = \unit[100 \times 100 \times
100]{\frac{g}{m^3}} = \unit[1\,000\,000]{\frac{g}{m^3}} =
\unit[1000]{\frac{kg}{m^3} }](../_images/math/a10d7928eabe85c8ce84cc49a5d4fc4ff025e98e.png)