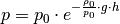Mechanik der Gase¶
In der Ärodynamik werden die mechanischen Eigenschaften von Gasen, insbesondere von Luft, untersucht.
Druck und Volumen¶
Ein wesentlicher Unterschied zwischen Gasen und Flüssigkeiten besteht darin,
dass Gase verhältnismäßig leicht komprimierbar sind; ihr Volumen  nimmt
also ab, wenn von außen ein erhöhter Druck
nimmt
also ab, wenn von außen ein erhöhter Druck  auf einen verformbaren
Gasbehälter (beispielsweise einen Luftballon) ausgeübt wird. Lässt der Druck
wieder nach, so nimmt entsprechend auch das Volumen des Gases wieder zu.
auf einen verformbaren
Gasbehälter (beispielsweise einen Luftballon) ausgeübt wird. Lässt der Druck
wieder nach, so nimmt entsprechend auch das Volumen des Gases wieder zu.
Bleibt die Temperatur des Gases während eines Kompressions- beziehungsweise Expansionsvorgangs konstant, so gilt:[1]
(1)¶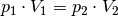
Wichtig: Für 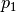 und
und 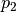 müssen bei Verwendung dieser Formel
stets absolute Druckwerte eingesetzt werden; zu einem mittels eines
Manometers gemessenen Druckwert muss also stets der Luftdruck (rund
müssen bei Verwendung dieser Formel
stets absolute Druckwerte eingesetzt werden; zu einem mittels eines
Manometers gemessenen Druckwert muss also stets der Luftdruck (rund
![\unit[1]{bar}](../../_images/math/6e104f5aba80ffafeaa668badd6fbfaa9bf2a2be.png) ) hinzu addiert werden.
) hinzu addiert werden.
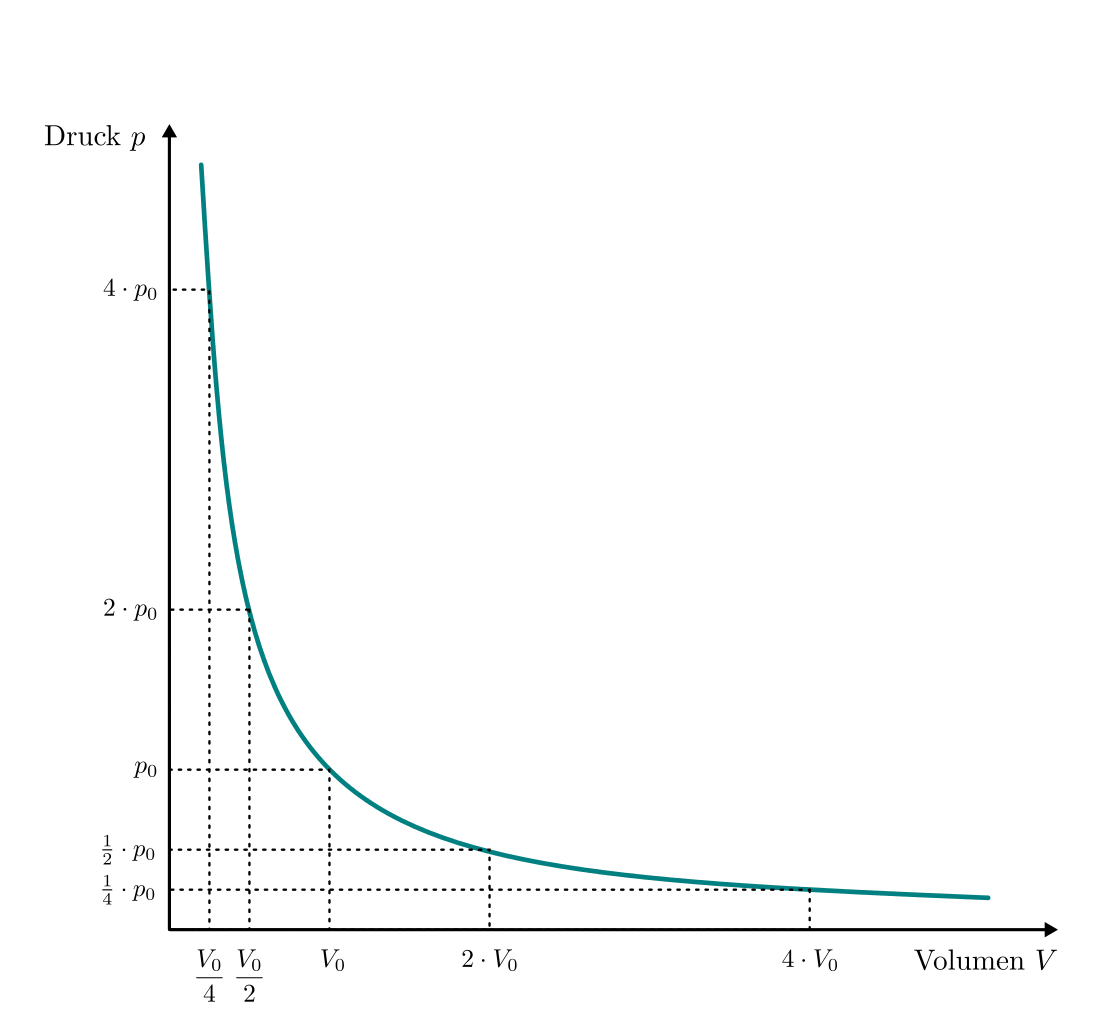
Die Volumina eines Gases verhalten sich sich also indirekt proportional zu den
jeweils vorherrschenden Druckwerten. Grafisch kann dieser Zusammenhang
mittels eines 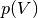 -Diagramms dargestellt werden:
-Diagramms dargestellt werden:
Die Kurve im 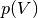 -Diagramm entspricht wegen
-Diagramm entspricht wegen 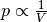 einer Hyperbel; man kann erkennen, dass das
Volumen des Gases auch bei sehr hohem Druck nicht gleich Null werden kann, und
umgekehrt durch eine zunehmende „Verdünnung“ der Luft ebenso immer ein Restdruck
verbleibt. Mittels so genannten Vakuumpumpen, die im Gegensatz zu Kompressoren
die Luft lediglich immer weiter verdünnen, kann somit kein echtes Vakuum erzeugt
werden, sondern nur ein sich asymptotisch an
einer Hyperbel; man kann erkennen, dass das
Volumen des Gases auch bei sehr hohem Druck nicht gleich Null werden kann, und
umgekehrt durch eine zunehmende „Verdünnung“ der Luft ebenso immer ein Restdruck
verbleibt. Mittels so genannten Vakuumpumpen, die im Gegensatz zu Kompressoren
die Luft lediglich immer weiter verdünnen, kann somit kein echtes Vakuum erzeugt
werden, sondern nur ein sich asymptotisch an ![p=\unit[0]{Pa}](../../_images/math/02b0dee9f7f30e66a045cf625aa4cda2e2112ff7.png) annähernder
Druckwert.
annähernder
Druckwert.
Luftdruck und Barometrische Höhenformel¶
Gase haben – im Verhältnis zu Flüssigkeiten – eine nur sehr geringe Masse.
Während ein Liter Wasser ein Kilogramm schwer ist, wiegt ein Liter Luft unter
Normalbedingungen gerade einmal knapp 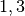 Gramm. Dennoch bewirkt auf
unserem Planeten das Gewicht der Luft, ähnlich wie beim Schweredruck in
Flüssigkeiten, einen so genannten Luftdruck, der umso größer
ist, je weiter unten man sich in dem die Erde umgebenden „Luftmeer“ befindet.
Gramm. Dennoch bewirkt auf
unserem Planeten das Gewicht der Luft, ähnlich wie beim Schweredruck in
Flüssigkeiten, einen so genannten Luftdruck, der umso größer
ist, je weiter unten man sich in dem die Erde umgebenden „Luftmeer“ befindet.
Der „normale“ Luftdruck ![p_0 \approx \unit[1,0]{bar}](../../_images/math/913c41e672e65889fdea547d88bdc872222bec0c.png) in Bodennähe
resultiert aus dem Gewicht der darüber liegenden Luftschichten. Da für
in Bodennähe
resultiert aus dem Gewicht der darüber liegenden Luftschichten. Da für
![\unit[1]{bar} = \unit[10^5]{Pa} = \unit[10^5]{\frac{N}{m^2}}](../../_images/math/2c6f6c0fd8c60fc80318d802fe73c9586a1b2e30.png) gilt,
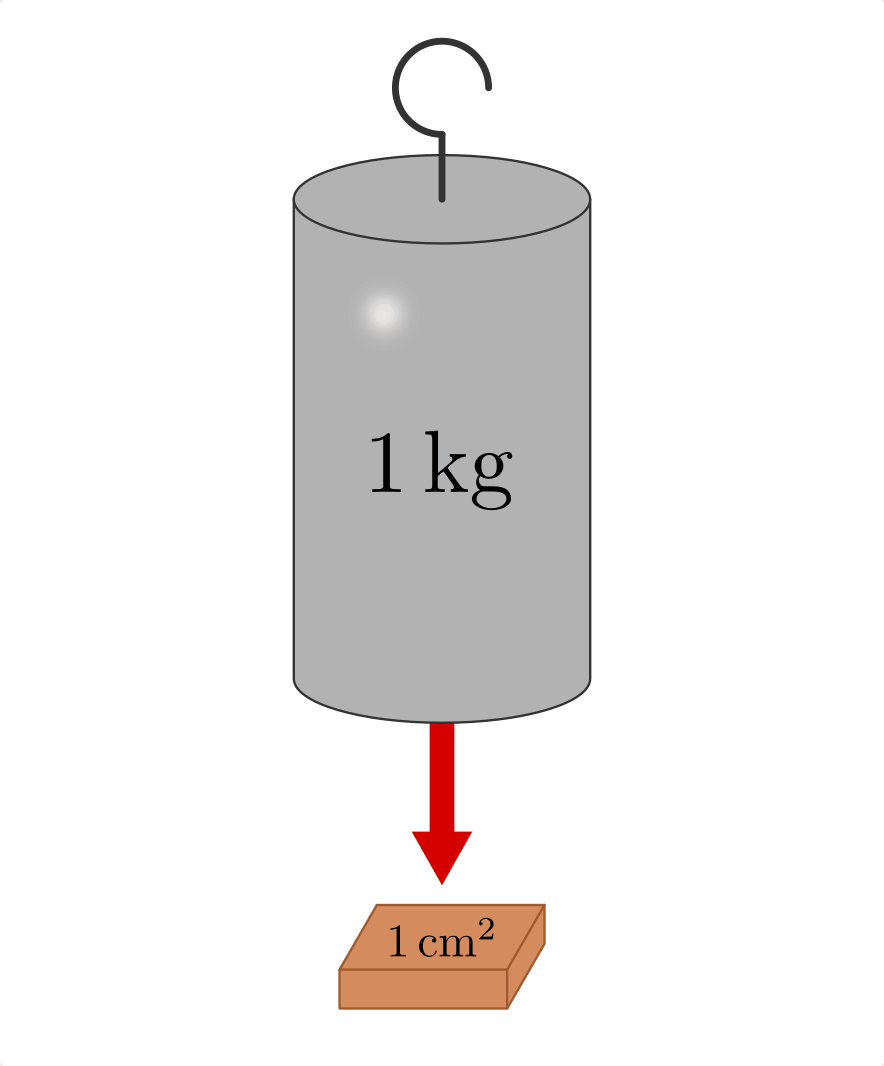
entspricht der durch die Luft ausgeübte Druck in Bodennähe rund einem Gewicht
von
gilt,
entspricht der durch die Luft ausgeübte Druck in Bodennähe rund einem Gewicht
von ![\unit[10]{t}](../../_images/math/b759f901929c71fdbf7349afe642395acd29f8df.png) je Quadratmeter beziehungsweise
je Quadratmeter beziehungsweise ![\unit[1]{kg}](../../_images/math/09b7dde1c3df0c3397d37923b9d2712730211373.png) je
Quadrat-Zentimeter.[2]
je
Quadrat-Zentimeter.[2]
Bei Standardbedingungen, das heißt einem Luftdruck von ![p_0 =
\unit[1,01325]{bar}](../../_images/math/f54022c4cc9995dff1add757c8703fe500fbdc50.png) und einer Temperatur von
und einer Temperatur von ![T_0 = \unit[0]{\degree C}](../../_images/math/fa57fe70bc8a96b2c59b4521c493a73228893dfe.png) nimmt ein Mol eines beliebigen Gases ein Volumen von
nimmt ein Mol eines beliebigen Gases ein Volumen von ![V_0 =
\unit[22,4]{l}](../../_images/math/24412b7972d8e75d80084a1b3ec96a6fbcea77d6.png) ein („Normalvolumen“). Da die
Masse eines Gases in einem geschlossenen System gleich bleibt, bewirkt eine
Veränderung des Gasvolumens
ein („Normalvolumen“). Da die
Masse eines Gases in einem geschlossenen System gleich bleibt, bewirkt eine
Veränderung des Gasvolumens  neben einer Veränderung des Drucks auch
eine Veränderung der Gasdichte
neben einer Veränderung des Drucks auch
eine Veränderung der Gasdichte 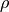 . Es gilt:[3]
. Es gilt:[3]
(2)¶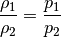
Bei einem niedrigem Gasdruck nimmt das Volumen eines Gases zu, seine Dichte
hingegen ab; in höheren Luftschichten ist daher die Luft „dünner“. Für den
Luftdruck  gilt in Abhängigkeit von der Höhe
gilt in Abhängigkeit von der Höhe 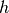 die so
genannte „barometrische Höhenformel“:[4]
die so
genannte „barometrische Höhenformel“:[4]
(3)¶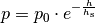
Hierbei ist 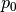 der Luftdruck auf Meereshöhe und
der Luftdruck auf Meereshöhe und 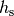 eine so genannte „Skalenhöhe“, die angibt, ab wie vielen Metern der Druck auf
eine so genannte „Skalenhöhe“, die angibt, ab wie vielen Metern der Druck auf
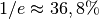 des ursprünglichen Werts
des ursprünglichen Werts 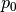 abfällt. Auf der
Erde ist
abfällt. Auf der
Erde ist ![h_{\mathrm{s}} \approx \unit[8,0]{km}](../../_images/math/ef88159acb8e5f26aa89b99ec8d7ec37976944db.png) . Die Höhe, bei welcher der
Luftdruck bzw. die Luftdichte nur noch halb so groß ist, liegt damit etwa bei
. Die Höhe, bei welcher der
Luftdruck bzw. die Luftdichte nur noch halb so groß ist, liegt damit etwa bei
![\unit[5,5]{km}](../../_images/math/56d6a6166623d05edae4013037e479f69cb9ce0b.png) .
.
Technisch wird der Zusammenhang zwischen Druck und Dichte beispielsweise in
Vakuumpumpen genutzt, mit deren Hilfe das zu evakuierende Luftvolumen
schrittweise verdünnt wird; im umgekehrten Fall kann mittels Kompressoren oder
Luftpumpen das Luftvolumen kontinuierlich verkleinert werden. Das Luftvolumen
kann jedoch nicht unendlich vergrößert oder verkleinert werden. Die Grenzen für
elektrische Vakuumpumpen liegen daher bei etwa ![\unit[10^{-2}]{mbar}](../../_images/math/8fb9ffd4c14c1aa46f00a2b26db0a60583f1532e.png) ;
mit mehrstufigen Hochvakuum-Pumpen können Drücke von rund
;
mit mehrstufigen Hochvakuum-Pumpen können Drücke von rund
![\unit[10^{-3}]{mbar}](../../_images/math/80674ad868210e1f428c19679afd7f658c139963.png) ) erreicht werden, mit Ultrahochvakuum-Pumpen sind
sogar Drücke von
) erreicht werden, mit Ultrahochvakuum-Pumpen sind
sogar Drücke von ![\unit[10^{-7}]{mbar}](../../_images/math/d58c9d8bebd3c54a2b2a7a8b7d05855f6b6141b7.png) möglich.[5] Im umgekehrten
Anwendungsfall kann man mit Luftpumpen bis zu
möglich.[5] Im umgekehrten
Anwendungsfall kann man mit Luftpumpen bis zu ![\unit[5]{bar}](../../_images/math/e9d9e64606c69ec152029f930281f3939cc53bd5.png) , mit
Kompressoren oder guten Stand-Luftpumpen bis zu
, mit
Kompressoren oder guten Stand-Luftpumpen bis zu ![\unit[12]{bar}](../../_images/math/6086d6dd6912287e6a978ee4cd2d4b737fd00ab8.png) erreichen.
erreichen.
Auftrieb in Gasen¶
Für die (statische) Auftriebskraft 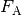 in Gasen gilt die gleiche
Formel wie für die Auftriebskraft in Flüssigkeiten:
in Gasen gilt die gleiche
Formel wie für die Auftriebskraft in Flüssigkeiten:
(4)¶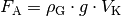
Hierbei bezeichnet 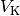 das Volumen des Körpers,
das Volumen des Körpers, ![g =
\unit[9,81]{\frac{N}{kg}}](../../_images/math/181c1511ef80f5055f390cec0a00f3b296715ab7.png) die Erdbeschleunigung und
die Erdbeschleunigung und 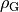 die Dichte des Gases. Da die Dichte von Luft
die Dichte des Gases. Da die Dichte von Luft ![\rho_{\mathrm{Luft}} \approx
\unit[1,3]{\frac{kg}{m^3}}](../../_images/math/7ee2659992f9556bed27a891566a0fc2c1294354.png) unter Normalbedingungen rund
unter Normalbedingungen rund 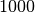 -mal
kleiner ist als die Dichte von Wasser
-mal
kleiner ist als die Dichte von Wasser ![(\rho_{\mathrm{Wasser}} =
\unit[1000]{\frac{kg}{m^3}})](../../_images/math/7a5d341db2282c12f20b8901d3731d6a1c6985b3.png) , können in Luft nur Körper mit einer sehr geringen
(durchschnittlichen) Dichte aufsteigen. Die Steighöhe beispielsweise von
Ballonen wird zudem dadurch begrenzt, dass die Dichte der Luft mit zunehmender
Höhe abnimmt.
, können in Luft nur Körper mit einer sehr geringen
(durchschnittlichen) Dichte aufsteigen. Die Steighöhe beispielsweise von
Ballonen wird zudem dadurch begrenzt, dass die Dichte der Luft mit zunehmender
Höhe abnimmt.
Anmerkungen:
| [1] | Die Gleichung (1) wird nach ihren Entdeckern Robert Boyle und Edme Mariotte „Gesetz von Boyle-Mariotte“ genannt und ist ein Sonderform der Zustandsgleichung für ideale Gase. |
| [2] | Nach der Zustandsgleichung für ideale Gase gilt
Der Term |
| [3] | Bei der Herleitung der barometrischen Höhenformel wird vom
Schweredruck in Flüssigkeiten ausgegangen; für den
Druckunterschied
Hierbei steht Bei konstanter Temperatur hängt bei Gasen die Dichte
Setzt man diesen Ausdruck für
Dividiert man beide Seiten dieser Gleichung durch
Wertet man die relativen Druckänderung für eine jeweils nur kleine
Höhenänderung aus, so kann man alle Änderungen von
Auf der linken Seite wurden die Integralgrenzen gemäß einer
Integration durch Substitution
umgerechnet. Auf der rechten Seite ist der Term
Das Integral auf der linken Seite kann ebenfalls unmittelbar berechnet
werden, wenn man
Mit Hilfe der Rechenregeln für Logarithmen kann der Term auf der linken Seite als
|
| [4] | Dieser Druck ist erheblich, wird aber von uns Menschen kaum wahrgenommen, da wir einen gleich großen Druck auch in unseren Lungen haben und daher nicht zusammengepresst werden. |
| [5] | Mit einfachen Wasserstrahlpumpen lässt sich ein Druck von rund
![\unit[10]{hPa}](../../_images/math/1082a187ea8b4d855e0ecb0403b6fb45c143fddd.png) erreichen. Für viele prinzipielle Versuche,
beispielsweise Magdeburger Halbkugeln oder Fallröhren reicht dieser Druck
bereits aus. erreichen. Für viele prinzipielle Versuche,
beispielsweise Magdeburger Halbkugeln oder Fallröhren reicht dieser Druck
bereits aus. |
Hinweis
Zu diesem Abschnitt gibt es Übungsaufgaben.

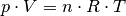 , wobei
, wobei  die (konstante) Stoffmenge in Mol und
die (konstante) Stoffmenge in Mol und ![R = \unit[8,31]{\frac{J}{mol
\cdot K}}](../../_images/math/8d4c699fa8b0d546d21e862c3b7ad265de251a25.png) die allgemeine Gaskonstante ist. Die Stoffmenge
die allgemeine Gaskonstante ist. Die Stoffmenge 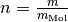 mit der Masse
mit der Masse
 des Gases verknüpft, wobei
des Gases verknüpft, wobei 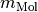 die
stoffspezifische molare Masse des Gases angibt. Es gilt also:
die
stoffspezifische molare Masse des Gases angibt. Es gilt also: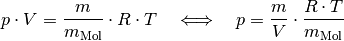
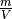 auf der rechten Gleichungsseite gibt die Dichte
des Gases an. Da
auf der rechten Gleichungsseite gibt die Dichte
des Gases an. Da 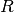 und
und 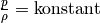 , also
, also 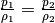 .
.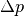 bei einem Höhenunterschied
bei einem Höhenunterschied 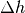 gilt:
gilt: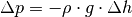
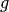 für den Ortsfaktor.
Das Minuszeichen ergibt sich daraus, dass der Druck mit zunehmender Höhe
geringer wird (da bei Flüssigkeiten
für den Ortsfaktor.
Das Minuszeichen ergibt sich daraus, dass der Druck mit zunehmender Höhe
geringer wird (da bei Flüssigkeiten 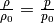 mit der Dichte
mit der Dichte 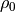 und dem Druck
und dem Druck ![h=\unit[0]{m}](../../_images/math/a79edaa5ff5fe49cba502f1f803321830791d490.png) zusammen. Umgeformt gilt also:
zusammen. Umgeformt gilt also: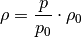
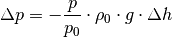
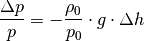
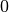 bis
bis 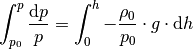
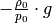 nicht von der Höhe
nicht von der Höhe 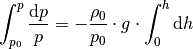
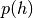 als Funktion der Höhe auffasst. Auf der linken
Gleichungsseite steht damit eine zusammengesetzte Funktion, deren Zähler der
Ableitung des Nenners entspricht. Mit der entsprechenden
als Funktion der Höhe auffasst. Auf der linken
Gleichungsseite steht damit eine zusammengesetzte Funktion, deren Zähler der
Ableitung des Nenners entspricht. Mit der entsprechenden
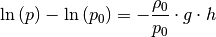
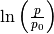 geschrieben werden. Um die resultierende
geschrieben werden. Um die resultierende
 mit den
jeweigen Termen potenzieren. Wegen
mit den
jeweigen Termen potenzieren. Wegen 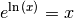 folgt
schließlich:
folgt
schließlich: