Zufallsexperimente und Ereignisse¶
Experimente, die unter gleichen Bedingungen zu gleichen Ergebnissen führen, bezeichnet man als determiniert. Im Rahmen der Wahrscheinlichkeitsrechnung werden hingegen meist zufällige Vorgänge betrachtet.
Zufallsexperimente
Als Experiment bezeichnet man allgemein einen Vorgang, der (zumindest prinzipiell) beliebig oft wiederholt werden kann. Dabei ist klar festgelegt, welche Messgröße beobachtet werden soll, jedes mögliche Ergebnis kann also eindeutig festgestellt werden. Eine einzelne Durchführung eines Experiments nennt man Versuch.
Ein Experiment, bei dem die Menge aller möglichen Ergebnisse bekannt ist, jedoch nicht das bei der Durchführung eines Versuchs tatsächlich eintretende Ergebnis, bezeichnet man als Zufallsexperiment.
Beispiel:
- In einer Urne befinden sich 50 gleichartige Kugeln mit den Nummern
 . Eine Kugel wird blind gezogen und anschließend ihre Nummer
notiert. Es können dabei 50 mögliche Ergebnisse auftreten, wobei die Nummer
der gezogenen Kugel
. Eine Kugel wird blind gezogen und anschließend ihre Nummer
notiert. Es können dabei 50 mögliche Ergebnisse auftreten, wobei die Nummer
der gezogenen Kugel 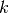 genannt wird.
genannt wird.
Für die einzelnen Versuchsergebnisse werden üblicherweise Kurzbezeichnungen
eingeführt, beispielsweise 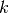 für das Ergebnis „Die gezogene Kugel hat
die Nummer
für das Ergebnis „Die gezogene Kugel hat
die Nummer 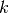 „. Alle möglichen Versuchsergebnisse fasst man zu einer so
genannten Ergebnismenge
„. Alle möglichen Versuchsergebnisse fasst man zu einer so
genannten Ergebnismenge 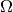 zusammen. Im obigen Fall gilt
beispielsweise:
zusammen. Im obigen Fall gilt
beispielsweise:
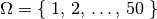
Die einzelnen, voneinander verschiedenen Ergebnisse eines Zufallsexperiments
werden allgemein mit 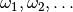 bezeichnet. Allgemein
besteht eine Ergebnismenge also aus folgenden Elementen:
bezeichnet. Allgemein
besteht eine Ergebnismenge also aus folgenden Elementen:
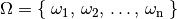
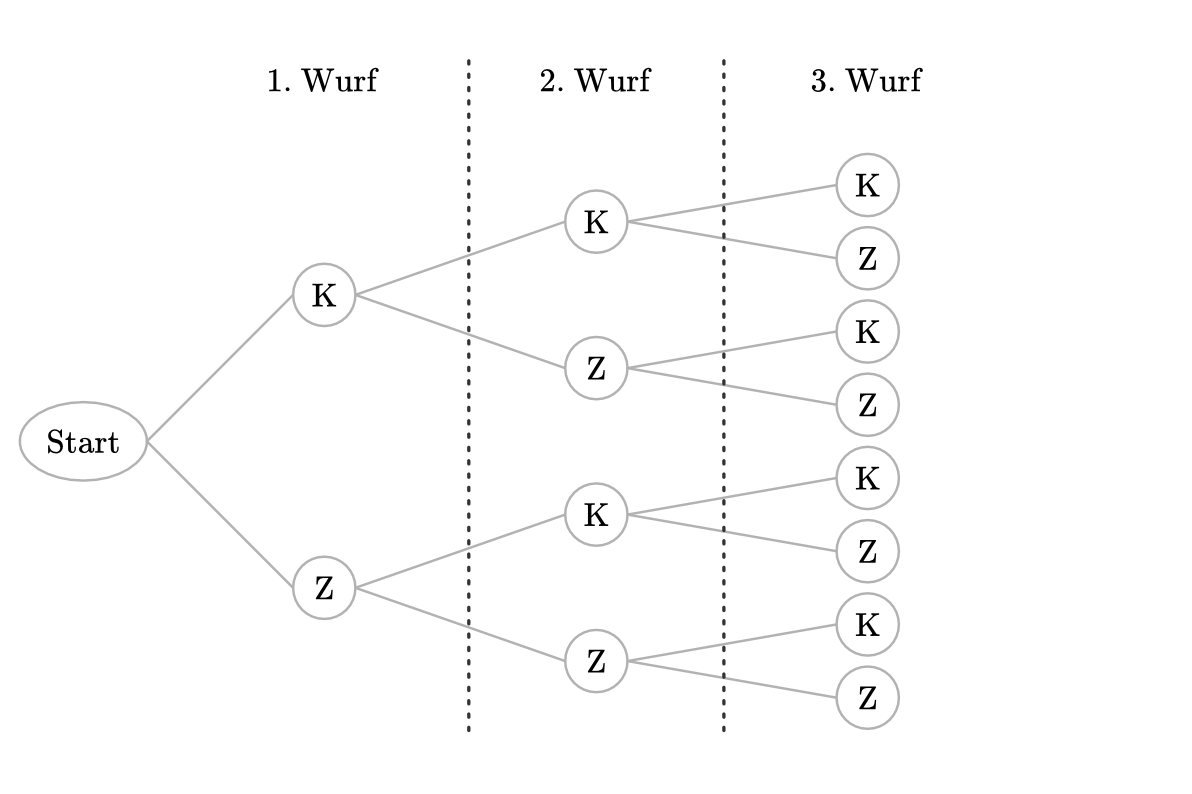
Mehrstufige Zufallsexperimente
Einstufige Zufallsexperimente, wie beispielsweise das Ziehen einer Kugel aus einer Urne, können zu mehrstufigen Zufallsexperimenten zusammengesetzt werden. Hierbei wird das zu Grunde liegende einstufige Zufallsexperiment mehrfach ausgeführt.
Beispiel:
Eine Münze wird zweimal geworfen. Bei jedem Wurf kann entweder das Ergebnis „Kopf“
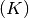 oder „Zahl“
oder „Zahl“ 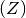 eintreten. Insgesamt lassen sich
die möglichen Versuchsergebnisse durch ein Tupel zweier Werte beschreiben. Für
die Ergebnismenge gilt in diesem Fall also:
eintreten. Insgesamt lassen sich
die möglichen Versuchsergebnisse durch ein Tupel zweier Werte beschreiben. Für
die Ergebnismenge gilt in diesem Fall also: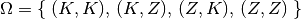
Die Ergebnismenge im obigen Beispiel lässt sich auch als Produktmenge 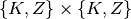 der Ergebnismengen eines
einmaligen Werfens einer Münze darstellen. Allgemein lässt sich ein
der Ergebnismengen eines
einmaligen Werfens einer Münze darstellen. Allgemein lässt sich ein
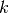 -stufiges Zufallsexperiment mit Hilfe von geordneten Zahlenpaaren der
Länge
-stufiges Zufallsexperiment mit Hilfe von geordneten Zahlenpaaren der
Länge 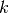 (so genannten „
(so genannten „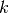 -Tupeln“) beschreiben.
-Tupeln“) beschreiben.
Eine Ergebnismenge kann durch einen so genannten Ergebnisbaum veranschaulicht werden. Jedem Ergebnis entspricht dabei einem Weg durch den Ergebnisbaum.
Ereignisse
Ereignisse werden formal durch Teilmengen von 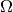 beschrieben.
beschrieben.
Beispiel:
Eine Urne enthält
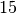 Kugeln, wobei je zwei Kugeln mit den Nummern
Kugeln, wobei je zwei Kugeln mit den Nummern
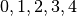 und je eine Kugel mit den Nummern
und je eine Kugel mit den Nummern 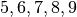 vorkommen. Es wird eine Kugel blind gezogen und ihre Nummer notiert, die
Ergebnismenge ist also
vorkommen. Es wird eine Kugel blind gezogen und ihre Nummer notiert, die
Ergebnismenge ist also 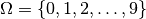 .
.Fasst man das Zufallsexperiment als Glücksspiel auf, bei dem man gewinnt, wenn eine Nummer
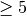 gezogen wird, so tritt dieses Ereignis genau
dann ein, wenn die gezogene Nummer gleich
gezogen wird, so tritt dieses Ereignis genau
dann ein, wenn die gezogene Nummer gleich 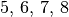 oder
oder 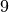 ist, das Versuchsergebnis also zur Menge
ist, das Versuchsergebnis also zur Menge 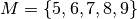 gehört.
Das Ereignis ist also durch die Menge
gehört.
Das Ereignis ist also durch die Menge 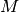 eindeutig beschrieben.
eindeutig beschrieben.
Allgemein beschreibt jede Teilmenge 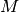 von
von 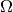 ein Ereignis.
Ist die Teilmenge mit
ein Ereignis.
Ist die Teilmenge mit 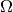 identisch
identisch 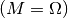 , so spricht
man von einem sicheren Ereignis, ist die Teilmenge gleich der leeren Menge
, so spricht
man von einem sicheren Ereignis, ist die Teilmenge gleich der leeren Menge
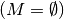 , so handelt es sich um ein unmögliches Ereignis.
Beinhaltet die Teilmenge genau ein Element
, so handelt es sich um ein unmögliches Ereignis.
Beinhaltet die Teilmenge genau ein Element  , so nennt man das
Ereignis elementar.[1]
, so nennt man das
Ereignis elementar.[1]
Die Menge aller möglichen Ereignisse, also die Menge aller Teilmengen von
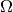 , heißt Ereignismenge
, heißt Ereignismenge 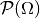 .[2]
.[2]
Da es sich bei Ereignissen um Mengen handelt, können diese ebenfalls durch Mengenoperationen miteinander verknüpft werden:
- Betrachtet man die Schnittmenge
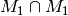 zweier Ereignisse, so
spricht man von einem UND-Ereignis (
zweier Ereignisse, so
spricht man von einem UND-Ereignis (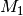 und
und 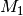 ).
). - Betrachtet man die Vereinigungsmenge
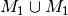 zweier Ereignisse, so
spricht man von einem ODER-Ereignis (
zweier Ereignisse, so
spricht man von einem ODER-Ereignis (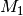 und
und 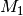 ).
). - Betrachtet man die Komplementmenge
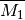 eines Ereignisses, so
spricht man von einem Gegenereignis (nicht
eines Ereignisses, so
spricht man von einem Gegenereignis (nicht 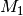 ).
).
Durch Bildung von Vereinigungs-, Schnitt- und Komplementmengen lassen sich nach den Rechenregeln der Mengenlehre weitere Ereignisse formulieren beziehungsweise Beschreibungen von Ereignissen vereinfacht werden.
Können zwei Ereignisse 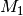 und
und 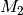 nicht gleichzeitig eintreten,
ist also
nicht gleichzeitig eintreten,
ist also 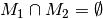 , so nennt man die Ereignisse
unvereinbar. Dies ist stets bei einem Ereignis
, so nennt man die Ereignisse
unvereinbar. Dies ist stets bei einem Ereignis 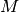 und dem entsprechenden
Gegenereignis
und dem entsprechenden
Gegenereignis 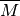 der Fall, es sind jedoch auch weitere Fälle
möglich.
der Fall, es sind jedoch auch weitere Fälle
möglich.
Beispiel:
Ein Würfel wird zweimal geworfen und jeweils die Augenzahl notiert. Dabei werden folgende Ereignisse betrachtet:
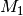 : „Die Summe der Augenzahlen ist gleich
: „Die Summe der Augenzahlen ist gleich 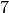 „, also
„, also
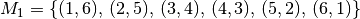 .
.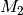 : „Pasch: Die beiden Augenzahlen sind gleich“, also
: „Pasch: Die beiden Augenzahlen sind gleich“, also 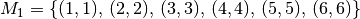 .
.
In diesem Beispiel gilt
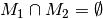 , die Ergeignisse sind
also unvereinbar.
, die Ergeignisse sind
also unvereinbar.
Anmerkungen:
| [1] | Zwischen dem Ergebnis  und dem Elementarereignis und dem Elementarereignis
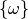 besteht ein formaler Unterschied: Während besteht ein formaler Unterschied: Während  ein Element der Ergebnismenge
ein Element der Ergebnismenge 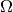 ist, ist ist, ist 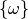 ein
Element der Ereignismenge ein
Element der Ereignismenge 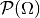 . . |
| [2] | In der Mengenlehre bezeichnet man 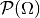 als
Potenzmenge von als
Potenzmenge von 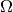 . Eine . Eine  -elementige Menge besitzt -elementige Menge besitzt
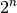 Teilmengen, für Teilmengen, für 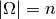 ist also ist also 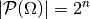 . Zu einem Zufallsexperiment mit einer . Zu einem Zufallsexperiment mit einer
 -elementigen Ergebnismenge gibt es also -elementigen Ergebnismenge gibt es also 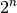 mögliche
Ereignisse. mögliche
Ereignisse. |
Hinweis
Zu diesem Abschnitt gibt es Übungsaufgaben.