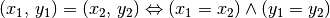Mengen und ihre Eigenschaften¶
Der Begriff „Menge“ wurde erstmals von Georg Cantor benutzt. Er bezeichnete damit eine „Zusammenfassung von bestimmten, klar unterscheidbaren Objekten unserer Anschauung und unseres Denkens zu einem Ganzen.“
Eine Menge (Kurzschreibweise: 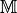 ) hat damit folgende
Eigenschaften:[1]
) hat damit folgende
Eigenschaften:[1]
- Eine Menge ist genau dann festgelegt, wenn sich von allen Objekten festlegen lässt, ob sie zur Menge gehören oder nicht.
- Ein Objekt darf nicht mehrfach in der Menge enthalten sein.
Die in einer Menge enthaltenen Objekte werden als Elemente bezeichnet.
Beispiele:
- Die Teilnehmer eines bestimmten Lehrgangs sind wohlunterschiedene Objekte unserer Anschauung, sie bilden also eine Menge.
- Die natürlichen Zahlen sind wohlunterschiedene Objekte unseres Denkens und bilden somit eine Menge.
- Die abstrakten Objekte
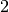 ,
, 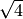 ,
, 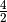 ,
,
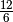 bilden eine einelementige Menge, da sie untereinander
gleich sind.
bilden eine einelementige Menge, da sie untereinander
gleich sind. - Die Menge der Primzahlen enthält unendlich viele Elemente.
- Die umgangssprachlichen Bezeichnungen: „eine Menge Geld“, „eine Menge Wasser“ usw. werden in der Mathematik nicht als Mengen angesehen, da sich nicht genau angeben lässt, welche Objekte dazugehören.
Als Variablen für Mengen werden Großbuchstaben, als Variablen für Elemente einer
Menge Kleinbuchstaben verwendet. 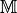 ist eine Menge, wenn für
jedes konkrete oder abstrakte Objekt
ist eine Menge, wenn für
jedes konkrete oder abstrakte Objekt  der Satz „
der Satz „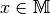 “ eine wahre oder falsche Aussage ist. Gehört zu einer Menge kein
konkretes oder abstraktes Objekt, so wird sie als leere Menge bezeichnet und mit
dem Symbol
“ eine wahre oder falsche Aussage ist. Gehört zu einer Menge kein
konkretes oder abstraktes Objekt, so wird sie als leere Menge bezeichnet und mit
dem Symbol 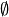 dargestellt.
dargestellt.
Die mathematische Kurzschreibweise 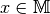 bedeutet, dass das Element
bedeutet, dass das Element
 in der Menge
in der Menge 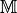 enthalten ist. Ist dieser Satz
enthalten ist. Ist dieser Satz
- für alle
 falsch, so ist
falsch, so ist 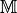 eine leere Menge,
eine leere Menge, - für endlich viele
 wahr, so ist
wahr, so ist 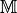 eine endliche Menge,
eine endliche Menge, - für unendlich viele
 wahr, so ist
wahr, so ist 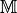 eine unendliche Menge.
eine unendliche Menge.
Ist ein Element  nicht in der Menge
nicht in der Menge 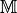 enthalten, so schreibt
man
enthalten, so schreibt
man 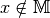 .
.
Darstellung von Mengen¶
Mengen lassen sich auf verschiedene Arten angeben:
- Aufzählende Form:
Die Symbole der Objekte werden in geschweiften Klammern, durch Komma getrennt, aufgelistet.
Beispiele:
- Kennzeichnende Form:
In der geschweiften Klammer wird eine Regel aufgeschrieben, anhand derer festgelegt ist, ob ein bestimmtes Element zur Menge gehört oder nicht.
Beispiel:
Die Schreibweise
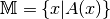 bedeutet
somit, dass genau dann
bedeutet
somit, dass genau dann 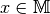 gilt, wenn die
Aussageform
gilt, wenn die
Aussageform 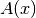 wahr ist.
wahr ist.
- Mengendiagramme:
Die Elemente der Menge werden innerhalb einer geschlossenen Kurve dargestellt („Venn-Diagramm“)
Mengengleichheit
Zwei Mengen  und
und 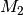 sind gleich,
wenn jedes Element von
sind gleich,
wenn jedes Element von  auch Element von
auch Element von
 ist, in Kurzschreibweise
ist, in Kurzschreibweise 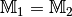 .
.
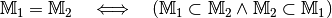
Teilmenge und Obermenge¶
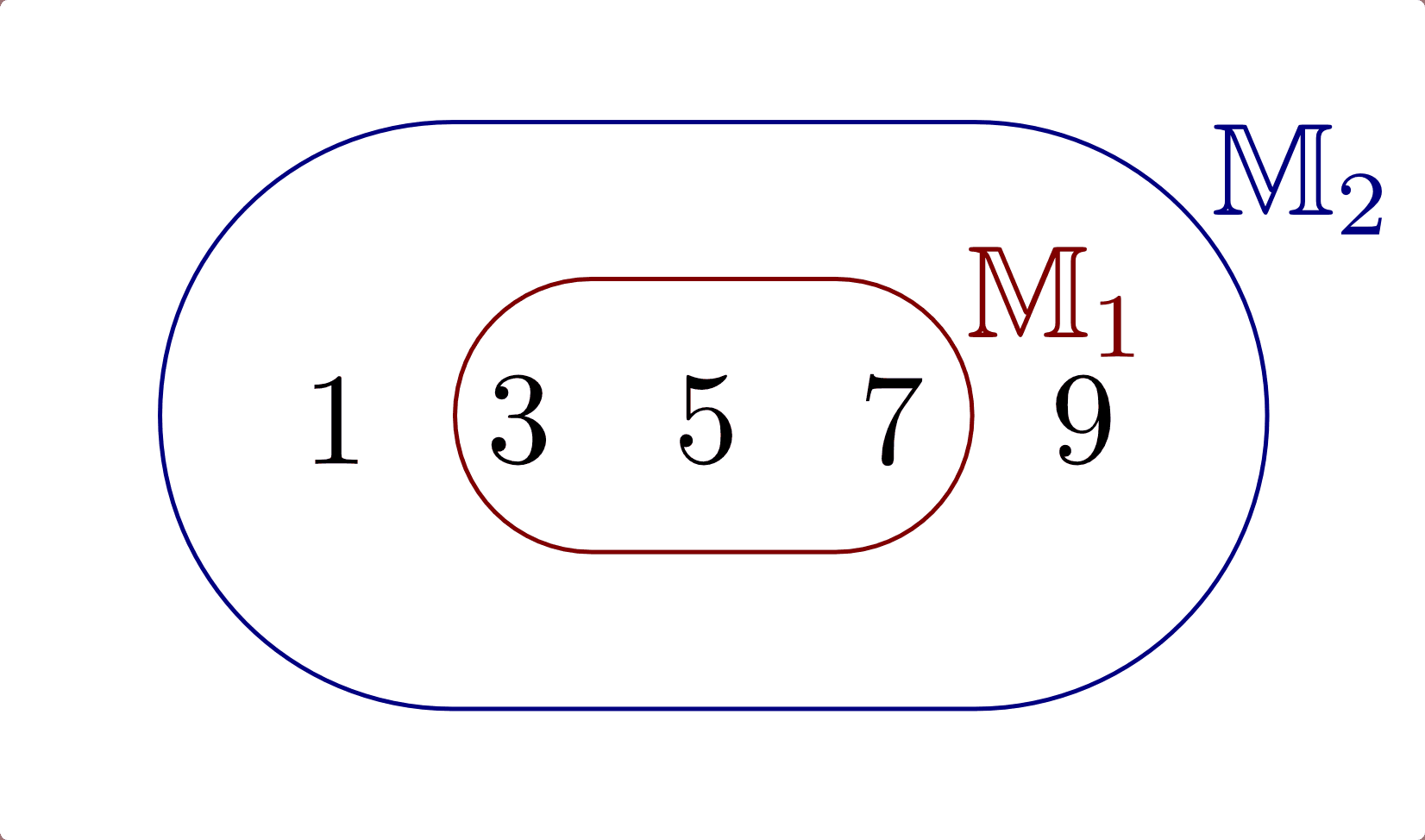
Sind alle Elemente der Menge  auch Elemente der Menge
auch Elemente der Menge
 , so ist
, so ist  eine Teilmenge
von
eine Teilmenge
von  , in Kurzschreibweise
, in Kurzschreibweise 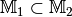 . Hierbei gibt es zwei Möglichkeiten:
. Hierbei gibt es zwei Möglichkeiten:
 heißt echte Teilmenge von
heißt echte Teilmenge von  , wenn
, wenn
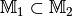 gilt und
gilt und  mindestens ein Element besitzt, das nicht zu
mindestens ein Element besitzt, das nicht zu  gehört.
gehört. heißt unechte Teilmenge von
heißt unechte Teilmenge von  , wenn
, wenn
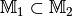 gilt und
gilt und  kein
Element besitzt, das nicht zu
kein
Element besitzt, das nicht zu  gehört – es gilt
gehört – es gilt
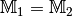 .
.
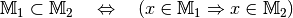
In beiden Fällen wird die Menge  , die auch alle
Elemente von
, die auch alle
Elemente von  enthält, als Obermenge von
enthält, als Obermenge von
 bezeichnet.
bezeichnet.
Beispiel:
Mengenoperationen¶
Die Schnittmenge¶
Unter der Schnittmenge zweier Mengen  und
und
 versteht man die Menge aller Objekte, die sowohl zu
versteht man die Menge aller Objekte, die sowohl zu
 als auch zu
als auch zu  gehören, in
Kurzschreibweise
gehören, in
Kurzschreibweise 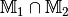 .
.
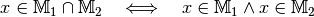
Beispiel:
Nach dem gleichen Prinzip lässt sich auch die Schnittmenge mehrerer Mengen bilden. Mengen, die keine gemeinsamen Elemente haben, werden als disjunkte oder elementefremde Mengen bezeichnet.
Die Vereinigungsmenge¶
Die Menge aller Objekte, die zu mindestens einer der Mengen  oder
oder  gehören, heißt Vereinigungsmenge von
gehören, heißt Vereinigungsmenge von
 und
und  , in Kurzschreibweise:
, in Kurzschreibweise:
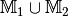 .
.
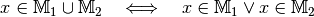
Beispiel:
Nach dem gleichen Prinzip lässt sich auch die Vereinigungsmenge mehrerer Mengen bilden.
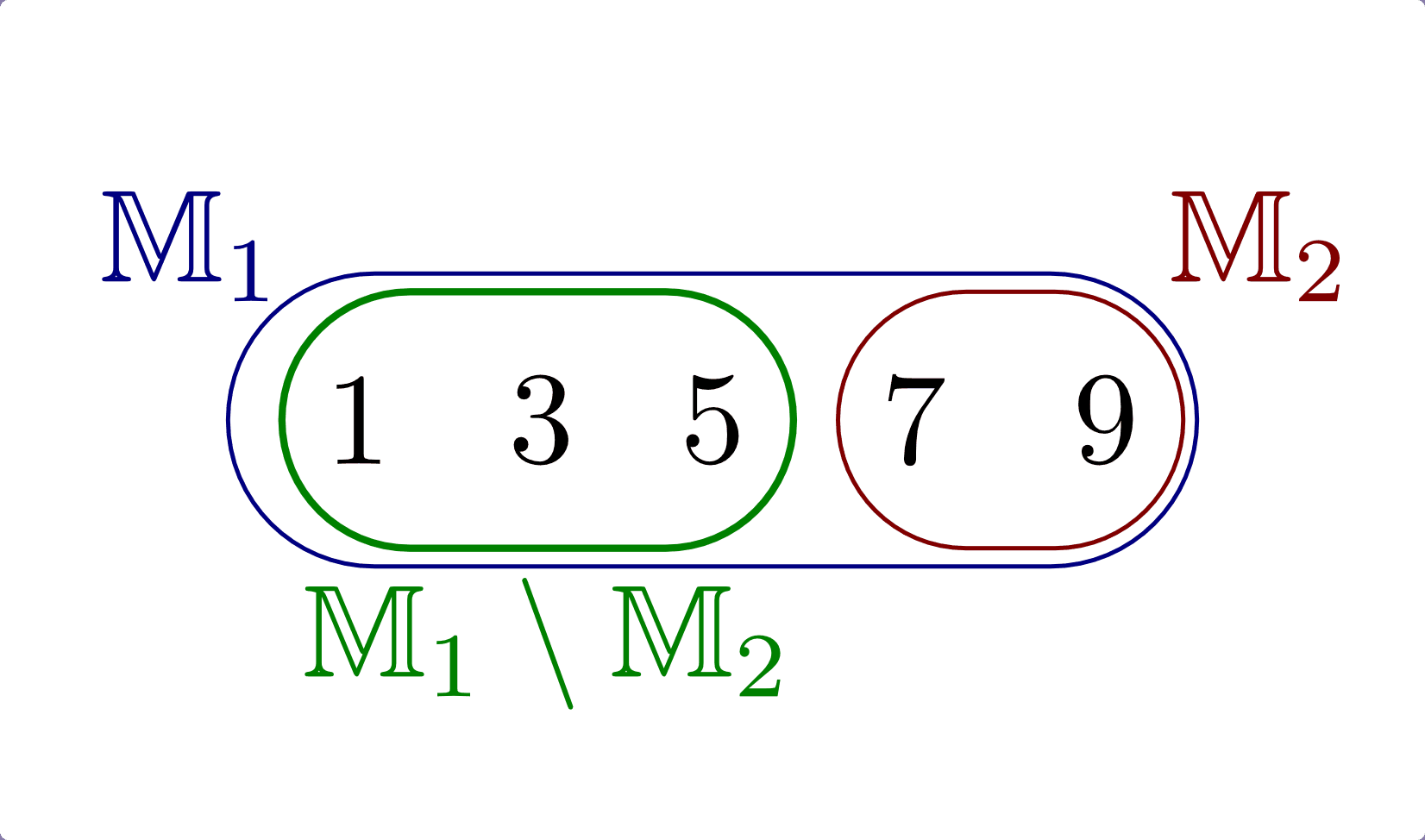
Die Differenz- und Komplementärmenge¶
Die Menge aller Objekte, die zu  gehören, ohne zugleich auch
zu
gehören, ohne zugleich auch
zu  zu gehören, heißt Differenzmenge (oder auch Restmenge)
der Mengen
zu gehören, heißt Differenzmenge (oder auch Restmenge)
der Mengen  und
und  , in Kurzschreibweise
, in Kurzschreibweise
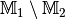 .
.
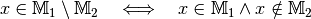
Beispiel:
Die Komplementärmenge  einer Menge
einer Menge  ist diejenige Menge bezüglich einer Obermenge
ist diejenige Menge bezüglich einer Obermenge 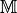 , deren Elemente
zwar zu
, deren Elemente
zwar zu 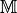 , aber nicht zu
, aber nicht zu  gehören. Somit
gilt
gehören. Somit
gilt 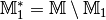 .
.
Die Produktmenge¶
Die Produktmenge (auch Kreuzmenge oder kartesisches Produkt) der Mengen
 und
und  ist die Menge sämtlicher
geordneter Paare, die mit den Elementen der Menge
ist die Menge sämtlicher
geordneter Paare, die mit den Elementen der Menge 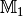 (an
erster Stelle) und denen der Menge
(an
erster Stelle) und denen der Menge  (an zweiter Stelle)
gebildet werden können, in Kurzschreibweise
(an zweiter Stelle)
gebildet werden können, in Kurzschreibweise 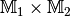 :[2]
:[2]
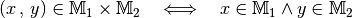
Ordnet man die Elemente von  als Punkte eines Zahlenstrahls
und die Elemente von
als Punkte eines Zahlenstrahls
und die Elemente von  auf einem dazu senkrecht stehenden
Zahlenstrahl an, dann stellen sich die Elemente
auf einem dazu senkrecht stehenden
Zahlenstrahl an, dann stellen sich die Elemente 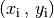 von
von 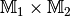 als Punkte der
Ebene dar, die von den beiden Zahlenstrahlen aufgebaut wird. Führt man diesen
Gedanken fort, so findet man, dass alle Punkte einer
als Punkte der
Ebene dar, die von den beiden Zahlenstrahlen aufgebaut wird. Führt man diesen
Gedanken fort, so findet man, dass alle Punkte einer 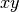 -Koordinatenebene
mit
-Koordinatenebene
mit 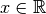 und
und 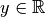 durch die Elemente von
durch die Elemente von
 dargestellt werden können.
dargestellt werden können.
Die Mächtigkeit von Mengen¶
Haben zwei endliche Mengen  und
und  die
gleiche Anzahl an Elementen, so bezeichnet man
die
gleiche Anzahl an Elementen, so bezeichnet man  und
und
 als gleichmächtig. Die Anzahl
als gleichmächtig. Die Anzahl 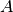 aller Elemente
einer endlichen Menge
aller Elemente
einer endlichen Menge 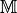 wird auch Kardinalzahl genannt.
wird auch Kardinalzahl genannt.
Die Abzählbarkeit
Die Mächtigkeit von unendlichen Mengen wird an der Menge der natürlichen
Zahlen 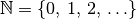 gemessen.
Lässt sich jedes Element einer Menge
gemessen.
Lässt sich jedes Element einer Menge 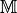 in eindeutiger Weise
einem Element aus
in eindeutiger Weise
einem Element aus 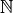 zuordnen, so wird die Menge
zuordnen, so wird die Menge
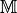 als abzählbar bezeichnet; die Elemente von
als abzählbar bezeichnet; die Elemente von
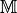 lassen sich also mit Hilfe der natürlichen Zahlen
„numerieren“.
lassen sich also mit Hilfe der natürlichen Zahlen
„numerieren“.
Beispiel:
- Jeder Zahl
 aus der Menge der natürlichen Zahlen
aus der Menge der natürlichen Zahlen 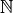 kann durch die Zuordnung
kann durch die Zuordnung 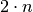 eine geradzahlige natürliche Zahl
zugeordnet werden. Die (unendliche) Menge der geradzahligen natürlichen
Zahlen ist somit ebenfalls abzählbar.
eine geradzahlige natürliche Zahl
zugeordnet werden. Die (unendliche) Menge der geradzahligen natürlichen
Zahlen ist somit ebenfalls abzählbar.
Ist eine Menge nicht abzählbar, wie beispielsweise die Menge 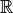 der reellen Zahlen, so wird sie überabzählbar genannt.
der reellen Zahlen, so wird sie überabzählbar genannt.
Anmerkungen:
| [1] | Genaugenommen lassen sich, wenn man den Begriff „Menge“ nicht genauer fasst, paradoxe Aussagen formulieren. Am bekanntesten ist die Russelsche Antinomie:
Durch eine Formulierung von bestimmten Bedingungen, die jede Menge erfüllen muss, konnten die Mathematiker Ernst Zermelo und Abraham Adolf Fränkel im Jahr 1930 eine widerspruchsfreie Mengenlehre einführen. Für die meisten alltäglichen Mathematik-Aufgaben genügt allerdings der ursprüngliche Mengenbegriff. |
| [2] | Ein Element
|
| [3] | Da hierbei die Reihenfolge der Zusammenfassung beliebig ist, kann auf die Klammern verzichtet werden. |
| [4] | Genau genommen entspricht die obige Darstellung nur der „linksseitigen“ Distributivität. Für zwei Mengen gilt jedoch ebenso die „rechtsseitige“ Distributivität:
Gelten sowohl die linksseitige wie auch die rechtsseitige Distributivität, wird allgemein von „Distributivität“ gesprochen. |
Hinweis
Zu diesem Abschnitt gibt es Übungsaufgaben.

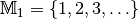
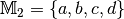
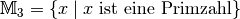
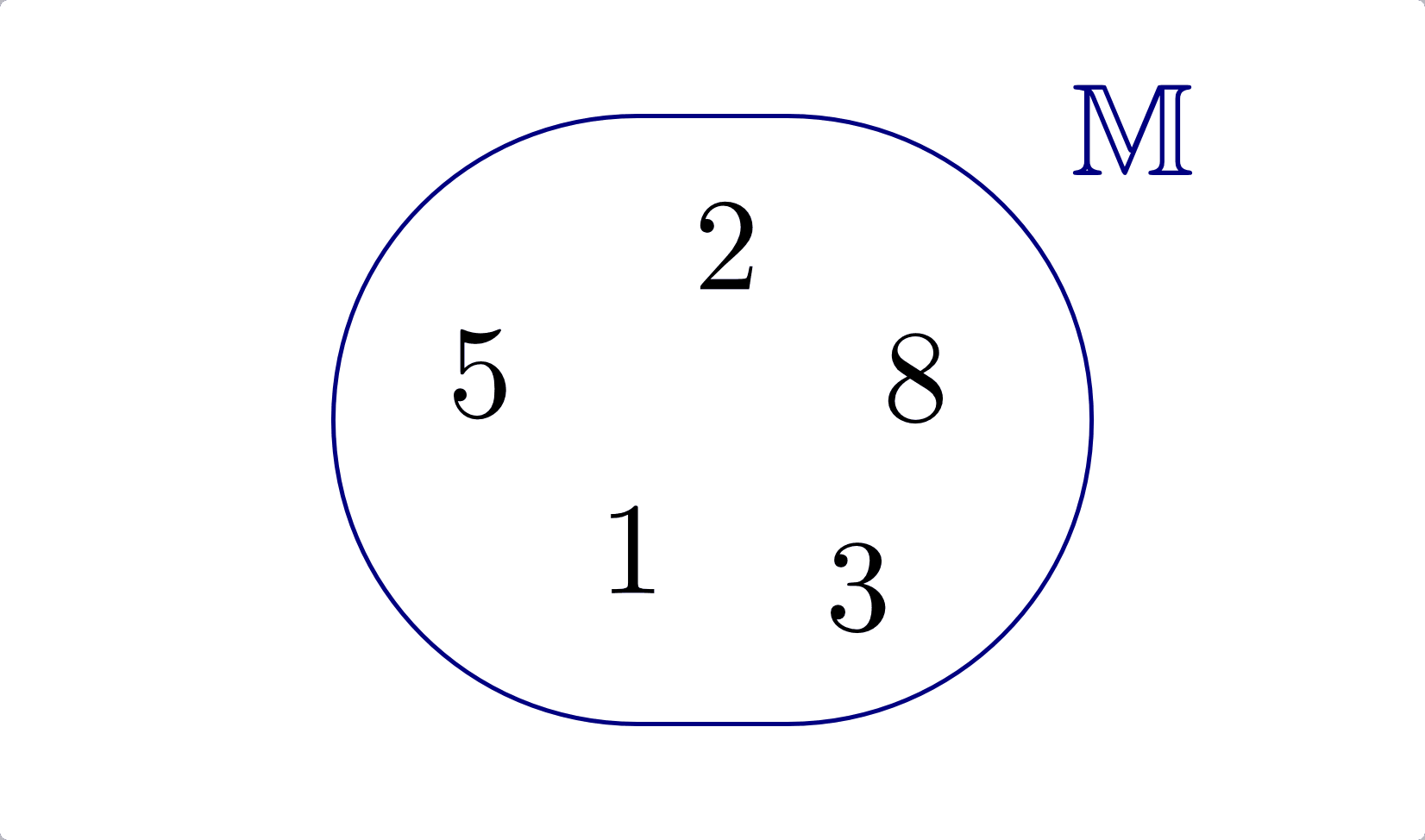
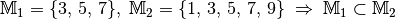
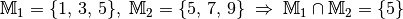
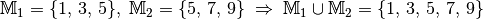
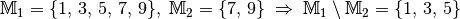

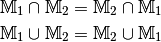

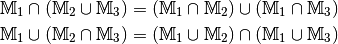
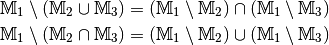
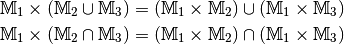
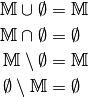
 einer Produktmenge ist nicht mit einer Menge
einer Produktmenge ist nicht mit einer Menge
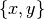 zu verwechseln. Während in letzterer die
Reihenfolge von
zu verwechseln. Während in letzterer die
Reihenfolge von  keine Rolle spielt, d.h.
keine Rolle spielt, d.h.
 gilt, sind zwei Elemente
einer Produktmenge nur gleich, wenn ihre Komponenten paarweise gleich sind,
wenn also gilt:
gilt, sind zwei Elemente
einer Produktmenge nur gleich, wenn ihre Komponenten paarweise gleich sind,
wenn also gilt: