Lösungen zur Mengenlehre¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Mengenlehre.
Eine Vereinigungsmenge enthält alle Elemente, die zu (mindestens) einer der beiden Teilmengen gehören. Für
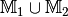 ergibt
sich im gegebenen Fall somit:
ergibt
sich im gegebenen Fall somit: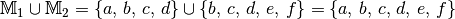
Eine Schnittmenge enthält alle Elemente, die gleichzeitig zu beiden Teilmengen gehören. Für
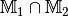 ergibt sich in den
einzelnen Fäll somit:
ergibt sich in den
einzelnen Fäll somit:![\begin{array}{>{\arraybackslash$}p{8cm}<{$} >{\arraybackslash$}p{8cm}<{$}}
\text{a) } \{ 1,\,2,\,3,\,4 \} \cap \{ 2,\,4,\,6,\,8,\,10 \} = \{ 2,\, 4 \}&
\text{b) } \{ a,\,b,\,c,\,d \} \cap \{ m,\,n,\,o,\,p,\,q \} = \emptyset \\[12pt]
\text{c) } \{ \frac{9}{3},\, 4,\, 5^2 \} \cap \{ 3^3,\, \sqrt{9},\, 7\} = \{ 3 \} &
\text{d) } \{ x \, | \; x < 5 \} \cap \{ x \, | \; x \ge 3 \} \\[4pt]
& \phantom{\text{d) }} = \{ x\,|\; 3 \le x < 5 \}\\[12pt]
\end{array}](../_images/math/0afb46b07df0c34fa878c208ac5474e01a2c2631.png)
Als Differenzmenge
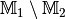 ergibt sich für
diese beiden Mengen:
ergibt sich für
diese beiden Mengen:![\mathbb{M}_1 \setminus \mathbb{M}_2 &= \{ 1,\, 2,\, 3,\, 4,\, 5,\, 6\} \setminus
\{ 4,\, 5,\, 6,\, 7,\, 8,\, 9,\, 10\} = \{ 1,\, 2,\, 3 \} \\[8pt]
\mathbb{M}_2 \setminus \mathbb{M}_1 &= \{ 4,\, 5,\, 6,\, 7,\, 8,\, 9,\, 10\} \setminus
\{ 1,\, 2,\, 3,\, 4,\, 5,\, 6\} = \{ 7,\, 8,\, 9,\, 10 \}](../_images/math/64029fb209dfabf0c55680d9200de25729aff919.png)
Es ist somit offensichtlich
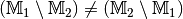 .
.
Abbildungen und Funktionen¶
Die folgenden Lösungen beziehen sich auf auf die Übungsaufgaben zum Abschnitt Abbildungen, Funktionen, Relationen und Operationen.
Die Abbildung kann als Teil der Produktmenge
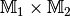 aufgefasst werden; bezeichnet man diese Teilmenge als
aufgefasst werden; bezeichnet man diese Teilmenge als 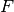 ,
so gilt:
,
so gilt: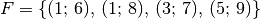
Die Abbildung ist keine Funktion, da das Element
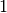 aus der Menge
aus der Menge
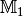 nicht eindeutig auf ein Element der Menge
nicht eindeutig auf ein Element der Menge
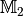 abgebildet wird.
abgebildet wird.
