Lösungen zur Logik¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Logik.
Die Gleichung stellt eine Aussageform dar, da in ihr als Charakteristikum (mindestens) eine unbestimmte Variable auftritt.
Weist man der Variablen den Wert
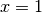zu, so geht die Aussageform über
in die Aussage 
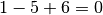, was offensichtlich als Wahrheitswert
„falsch“ hat. Weist man der Variablen hingegen den Wert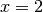 
zu, so
ergibt sich die wahre Aussage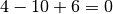 
.
Die mathematiche Kurzschreibweise für „10 ist Teiler von
“ lautet
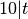(„Zehn teilt „). Da es sich bei der Aussage um eine
Folgerung („Implikation“) handelt, kann also geschrieben werden: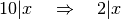
Die beiden Aussagen lassen sich nur mit einer Implikation sinnvoll verknüpfen. Jedes Quadrat hat vier gleich große Innenwinkel. Umgekehrt ist jedes Viereck mit vier gleich großen Innenwinkel zwar ein Rechteck, aber nicht zwingend ein Quadrat. Zusammengefasst gilt also:
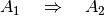
Wird die zweite Aussage um den Zusatz „und es hat gleich lange Seiten“ ergänzt, so sind die erste und die zweite Aussage äquivalent zueinander. In diesem Fall kann man also schreiben:
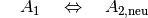
Bei einer UND-Verknüpfung müssen beide Bedingungen gleichzeitig erfüllt sein, damit ihr Wahrheitswert „wahr“ ist (die Aussage also zutrifft). Demnach wäre es bei der Anweisung „Rauchen UND Umgang mit offenen Licht ist verboten!“ aus rein logischer Sicht immer noch erlaubt, entweder zu rauchen oder Umgang mit offenem Licht zu haben; es darf nur nicht beides zugleich eintreten. In der Praxis ist es allerdings wohl auch bei einer derart schlampig formulierten Warnung empfehlenswert, sicherheitshalber beides zu unterlassen…
Bei dem wohl eher in Kneipen anzutreffenden Wandspruch „drink OR drive“ sollte es wohl eher „drink XOR drive“ heißen, denn so gilt die ODER-Verknüpfung für die Fälle „not drink and drive“ und „drink and not drive“, allerdings auch für „drink and drive“. Insbesondere vor letzterem ist aber dringend abzuraten…
Während des Studiums hieß es bei uns daher: „Don’t drink and d(e)rive!“ ;-)
Durch eine Adjunktion der Aussagen
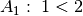und 
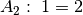entsteht die Aussage 
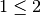. Die Aussage 
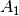ist wahr, die
Aussage 
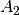hingegen ist falsch. Die ODER-Verknüpfung beider Aussagen
ist wahr (da zumindest eine der beiden Teilaussagen wahr ist).
Durch eine Konjunktion der Aussagen
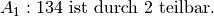und 
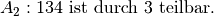entsteht die
Aussage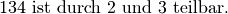 
? Die Aussage
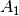ist wahr, die Aussage 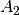hingegen ist falsch.
Die UND-Verknüpfung beider Aussagen ist falsch (die nicht beide Aussagen
zugleich wahr sind).
Die Antivalenz der beiden Aussagen ergibt die Aussage „Der Zug fährt entweder nach Hamburg oder Berlin“. Ob der Wahrheitswert dieser Gesamt-Aussage wahr oder falsch ist, hängt selbstverständlich vom jeweiligen Zug ab. Wir können allerdings o.B.d.A. annehmen, der Zug sei intakt und habe nur genau diese zwei Fahrt-Optionen: Dann trifft stets genau eine der beiden Aussagen zu (niemals keine, niemals beide zugleich).
Die Implikation beider Aussagen liefert die Gesamt-Aussage „Wenn die Erde ein Würfel ist, dann ist die Sonne eine Pyramide.“ Beide Teil-Aussagen sind falsch, die Implikation hingegen richtig (da eine Folgerung aus einer falschen Aussage definitionsgemäß stets wahr ist).
Die Adjunktion (ODER-Verknüpfung) einer wahren und einer falschen Aussage (im Computer-Bereich: „Bedingung“) ist stets wahr; die Gesamt-Aussage ergibt somit den logischen Wert „wahr“.