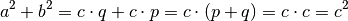Dreiecke¶
Allgemeine Eigenschaften¶
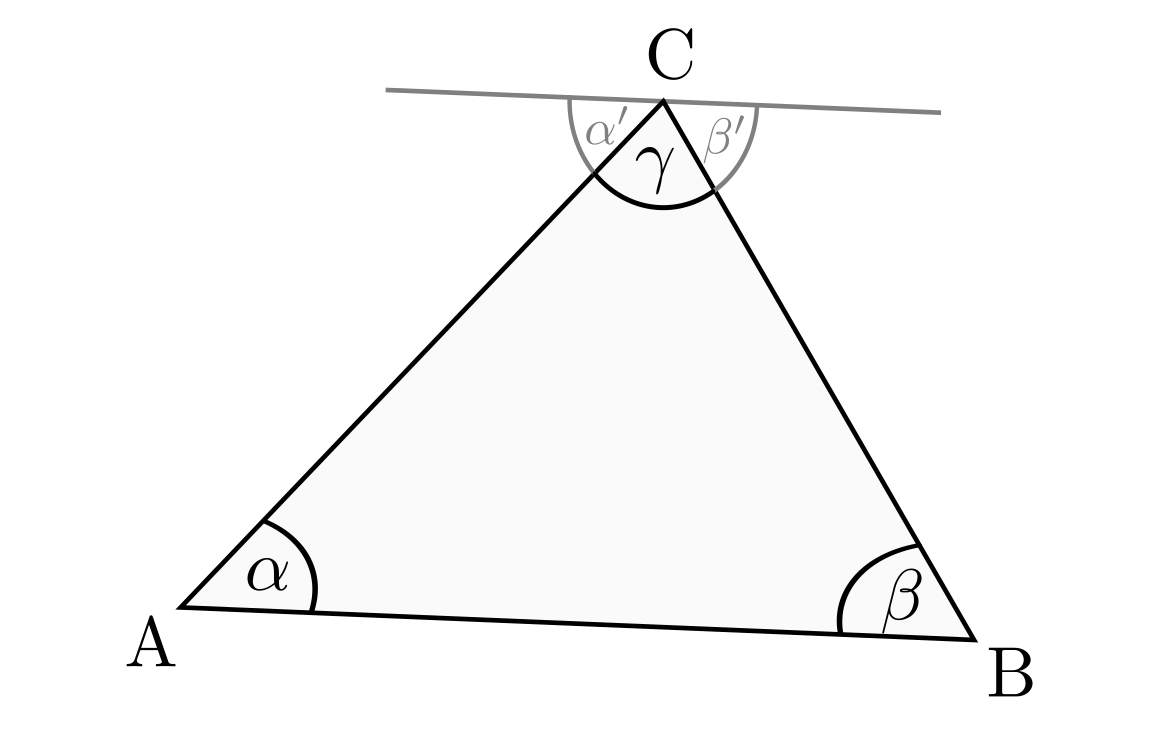
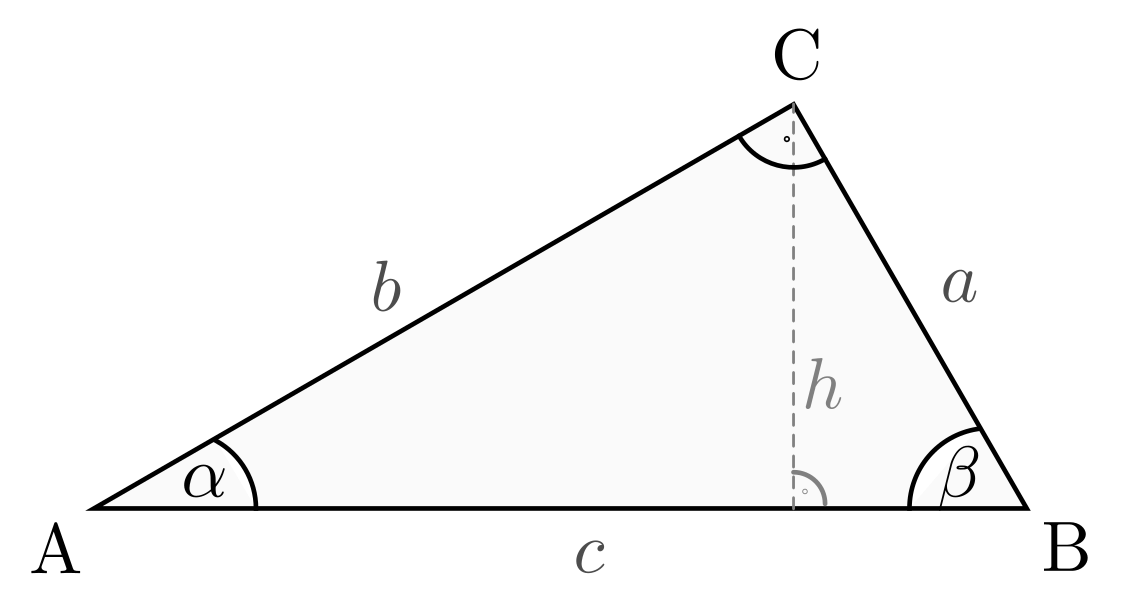
Dreiecke bestehen aus den Verbindungsstrecken zwischen drei Punkten
 ,
,  und
und  , die nicht auf
einer gemeinsamen Geraden liegen. Die den Punkten jeweils gegenüber liegenden
Strecken werden kurz als
, die nicht auf
einer gemeinsamen Geraden liegen. Die den Punkten jeweils gegenüber liegenden
Strecken werden kurz als  ,
,  und
und  , die Innenwinkel als
, die Innenwinkel als
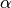 ,
,  und
und 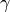 bezeichnet. Die Nebenwinkel
bezeichnet. Die Nebenwinkel
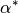 ,
, 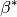 und
und 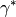 der Innenwinkel
heißen Außenwinkel.
der Innenwinkel
heißen Außenwinkel.
Legt man durch  eine Parallele zu Strecke
eine Parallele zu Strecke
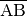 , so sind
, so sind 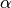 und
und 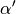 sowie
sowie
 und
und 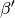 als Wechselwinkel gleich groß. Gemeinsam mit dem Winkel
als Wechselwinkel gleich groß. Gemeinsam mit dem Winkel 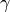 bilden
bilden
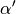 und
und 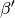 einen
einen ![\unit[180]{\degree}](../../_images/math/a62139d45d177455d34d6e27e1030722257dea2f.png) -Winkel. Die
Summe der Innenwinkel
-Winkel. Die
Summe der Innenwinkel 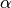 ,
,  und
und 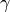 ist somit
ebenfalls stets
ist somit
ebenfalls stets ![\unit[180]{\degree}](../../_images/math/a62139d45d177455d34d6e27e1030722257dea2f.png) :
:
(1)¶![\alpha + \beta + \gamma = \unit[180]{\degree}](../../_images/math/35d8448e0eb419d4c61f074ac6e2f201af0fcc04.png)
Die Außenwinkel sind jeweils so groß wie die Summe der beiden nicht anliegenden
Innenwinkel. Dies folgt beispielsweise für den Winkel 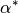 aus
Gleichung (1) wegen
aus
Gleichung (1) wegen  . Insgesamt gilt:
. Insgesamt gilt:
(2)¶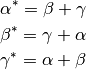
Die Summe der Außenwinkel eines Dreiecks beträgt 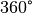 .
Weiterhin gelten in allen Dreiecken drei weitere Beziehungen:
.
Weiterhin gelten in allen Dreiecken drei weitere Beziehungen:
Die Summe zweier Seitenlängen ist stets größer als die Länge der dritten Seite. Es gelten somit folgende Ungleichungen:
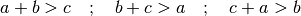
Die Differenz zweier Seitenlängen ist stets kleiner als die Länge der dritten Seite. Somit gilt:
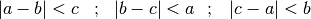
- In jedem Dreieck liegen die größeren Seiten den größeren Winkeln gegenüber.Umgekehrt liegen die größeren Winkel den größeren Seiten gegenüber. Es gilt somit beispielsweise:
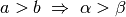
Kongruenz und Ähnlichkeit¶
Zwei Dreiecke sind dann kongruent, wenn sie eine der folgenden Bedingungen erfüllen:
- Übereinstimmung dreier Seiten (SSS)
- Übereinstimmung zweier Seiten und dem von ihnen eingeschlossenen Winkel (SWS)
- Übereinstimmung zweier Seiten und dem der größeren Seite gegenüber liegenden Winkel (SSW)
- Übereinstimmung einer Seite und zweier Winkel – entweder den beiden anliegenden Winkeln oder einem anliegenden und einem gegenüber liegenden Winkel (WSW beziehungsweise SWW)
Die obigen Kongruenzbedingungen werden einerseits für geometrische Beweise genutzt, können jedoch auch zur eindeutigen Festlegung von Dreiecken verwendet werden.
Zwei Dreiecke sind dann einander ähnlich, wenn sie eine der folgenden Bedingungen erfüllen:
- Gleiche Längenverhältnisse aller drei Seiten
- Gleiche Längenverhältnisse zweier Seiten und Übereinstimmung des von ihnen eingeschlossenen Winkels
- Gleiche Längenverhältnisse zweier Seiten und Übereinstimmung des der größeren Seite gegenüber liegenden Winekls
- Übereinstimmung zweier Winkel
Beispielsweise lassen sich die Zentrische Streckung oder die Strahlensätze auf Ähnlichkeiten von Dreiecken zurückführen.
Besondere Punkte im Dreieck¶
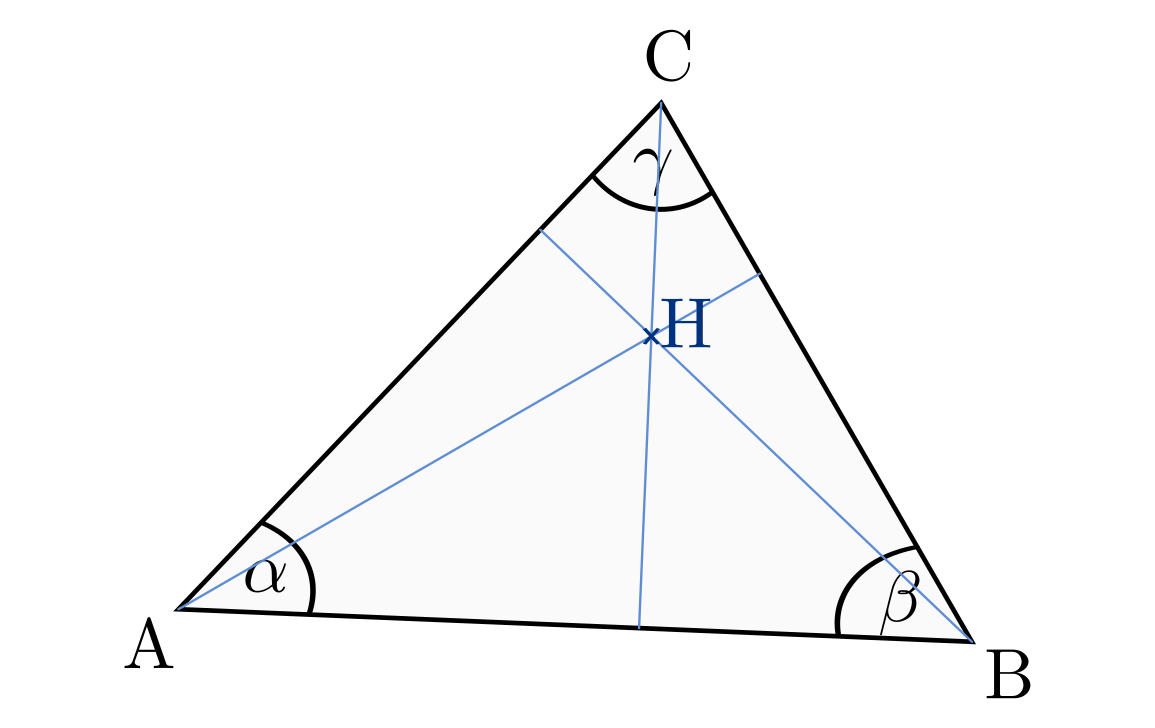
In jedem Dreieck gibt es vier besondere Punkte, die sich durch bestimmte Transversalen, d.h. durch das Dreieck verlaufende Geraden, konstruieren lassen. Alle diese Punkte liegen auf einer gemeinsamen Geraden, die auch „Eulersche Gerade“ genannt wird.
Der Schwerpunkt
Verbindet man jeden Eckpunkt mit dem Mittelpunkt der gegenüber liegenden
Dreiecksseite, so schneiden sich diese „Seitenhalbierenden“ in einem gemeinsamen
Punkt  , der Schwerpunkt des Dreiecks genannt wird.
, der Schwerpunkt des Dreiecks genannt wird.
Der Schwerpunkt teilt die Seitenhalbierenden jeweils im Verhältnis 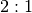 .
Es bestehen also folgende Proportionen:
.
Es bestehen also folgende Proportionen:
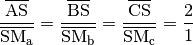
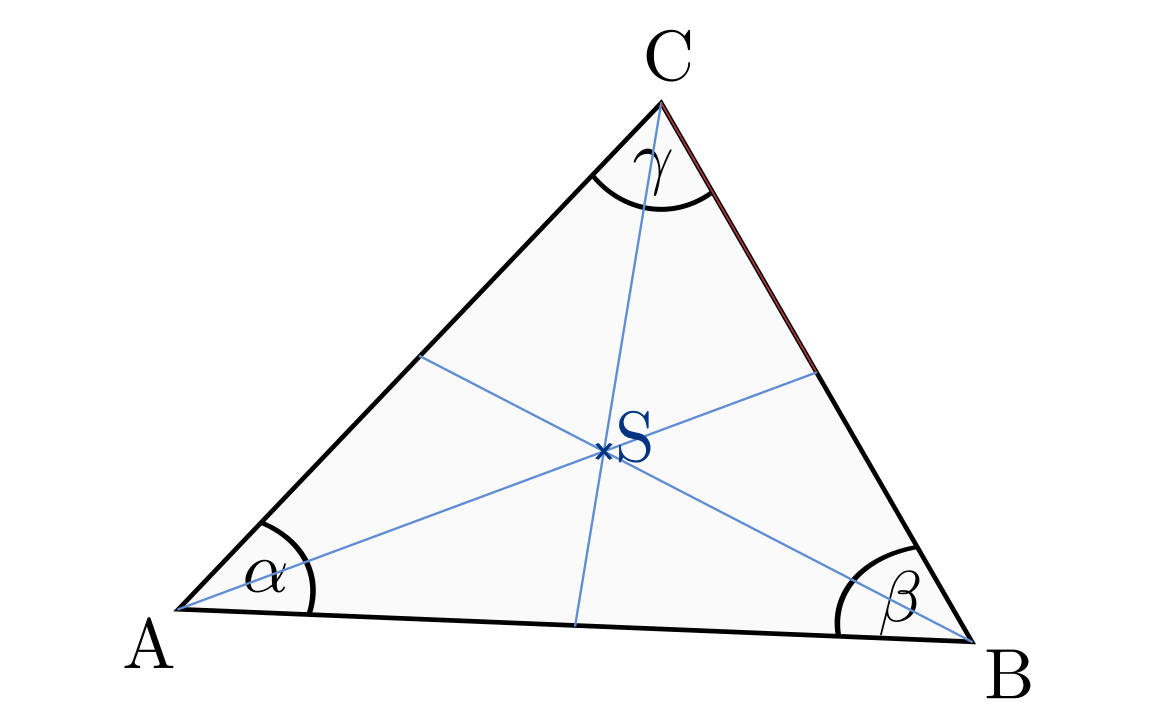
Der Mittelpunkt
Zeichnet man auf jeder Dreeicksseite den Mittelpunkt ein und konstruiert
ausgehend von diesem eine senkrechte Gerade zur jeweiligen Dreiecksseite, so
schneiden sich diese „Mittelsenkrechten“ in einem gemeinsamen Punkt
 . Dieser Punkt wird Mittelpunkt des Dreeicks genannt und ist der
Mittelpunkt des so genannten Umkreises, also des Kreises, der durch alle
Eckpunkte des Dreiecks verläuft.
. Dieser Punkt wird Mittelpunkt des Dreeicks genannt und ist der
Mittelpunkt des so genannten Umkreises, also des Kreises, der durch alle
Eckpunkte des Dreiecks verläuft.
Der Mittelpunkt des Inkreises
Konstruiert man zu jedem Innenwinkel eines Dreiecks die Winkelhalbierende, so
schneiden sich diese in einem gemeinsamen Punkt  . Dieser ist
zugleich der Mittelpunkt des Inkreises, also des Kreises, der alle Strecken des
Dreiecks berührt.
. Dieser ist
zugleich der Mittelpunkt des Inkreises, also des Kreises, der alle Strecken des
Dreiecks berührt.
Der Höhenschnittpunkt
Konstruiert man auf jeder Dreiecksseite eine Senkrechte durch den gegenüber
liegenden Eckpunkt, so schneiden sich die drei Höhen in einem gemeinsamen Punkt
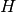 .
.
Besondere Dreiecke¶
Gleichseitiges Dreieck¶
In einem gleichseitigen Dreieck besitzen alle Seiten die gleiche Länge. Alle
Winkel betragen ![\unit[60]{\degree}](../../_images/math/29240e711012ec5c575a011aa368385d7725392a.png) , die besonderen Punkte
, die besonderen Punkte
 ,
, 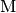 ,
, 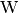 und
und
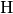 sind in einem Punkt vereint.
sind in einem Punkt vereint.
Für die Fläche und den Umfang eines gleichseitigen Dreiecks gilt mit der Höhe
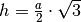 :
:
![\text{Fl\"ache} &= \frac{1}{2} \cdot a \cdot h = \frac{a^4}{4} \cdot
\sqrt{3} \\[10pt]
\text{Umfang} &= 3 \cdot a](../../_images/math/d55c52c075668d60d7157692c9d5ead331ae73c0.png)
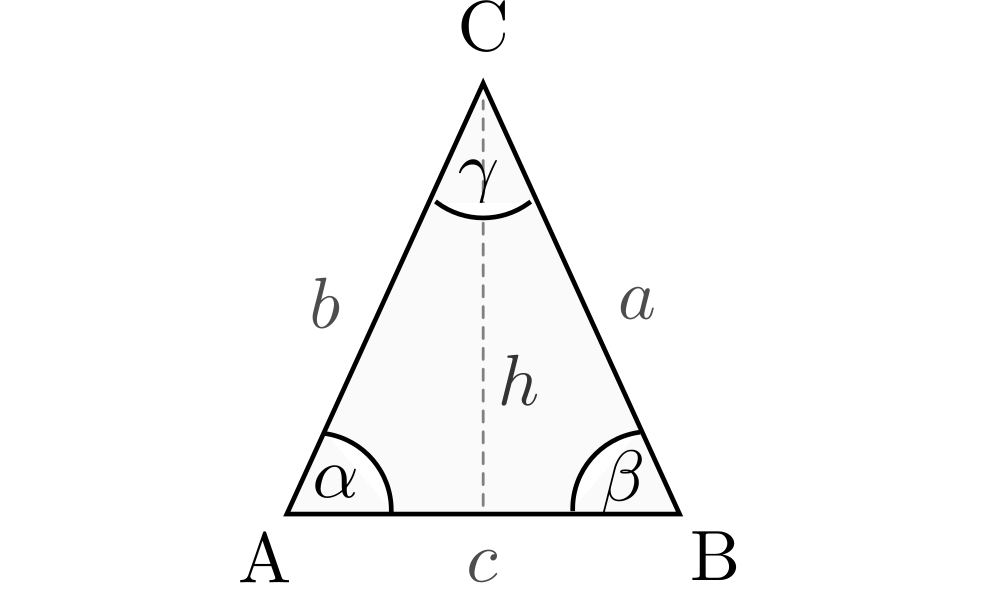
Gleichschenkliges Dreieck¶
In einem gleichschenkligen Dreieck besitzen die zwei Seiten  und
und
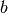 die gleiche Länge. Die beiden „Basiswinkel“
die gleiche Länge. Die beiden „Basiswinkel“ 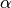 und
und
 sind gleich groß. Ist ein Winkel bekannt, lassen sich die übrigen
Winkel unmittelbar mit Hilfe der Beziehung
sind gleich groß. Ist ein Winkel bekannt, lassen sich die übrigen
Winkel unmittelbar mit Hilfe der Beziehung 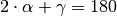 bestimmen.
bestimmen.
Für die Fläche und den Umfang eines gleichschenkligen Dreiecks gilt mit der Höhe
 :
:
![\text{Fl\"ache} &= \frac{1}{2} \cdot c \cdot h \\[10pt]
\text{Umfang} &= 2 \cdot a + c](../../_images/math/b2f632694b8dfd6cdda84936bed05e1dfc682a98.png)
Rechtwinkliges Dreieck¶
In einem rechtwinkligen Dreieck ist ein Winkel gleich
![\unit[90]{\degree}](../../_images/math/ed42da9b82869c64cf4a98987530ceace4d59e0e.png) , die anderen beiden Winkel
, die anderen beiden Winkel 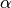 und
und
 ergeben zusammen
ergeben zusammen ![\unit[90]{\degree}](../../_images/math/ed42da9b82869c64cf4a98987530ceace4d59e0e.png) .[1]
.[1]
Für die Fläche und den Umfang eines rechtwinkligen Dreiecks gilt:[2]
![\text{Fl\"ache} &= \frac{1}{2} \cdot a \cdot b = \frac{1}{2} \cdot c \cdot h
\\[10pt]
\text{Umfang} &= a + b + c](../../_images/math/6bac9b70e0f70967dde57760cf324ba5ecfb5456.png)
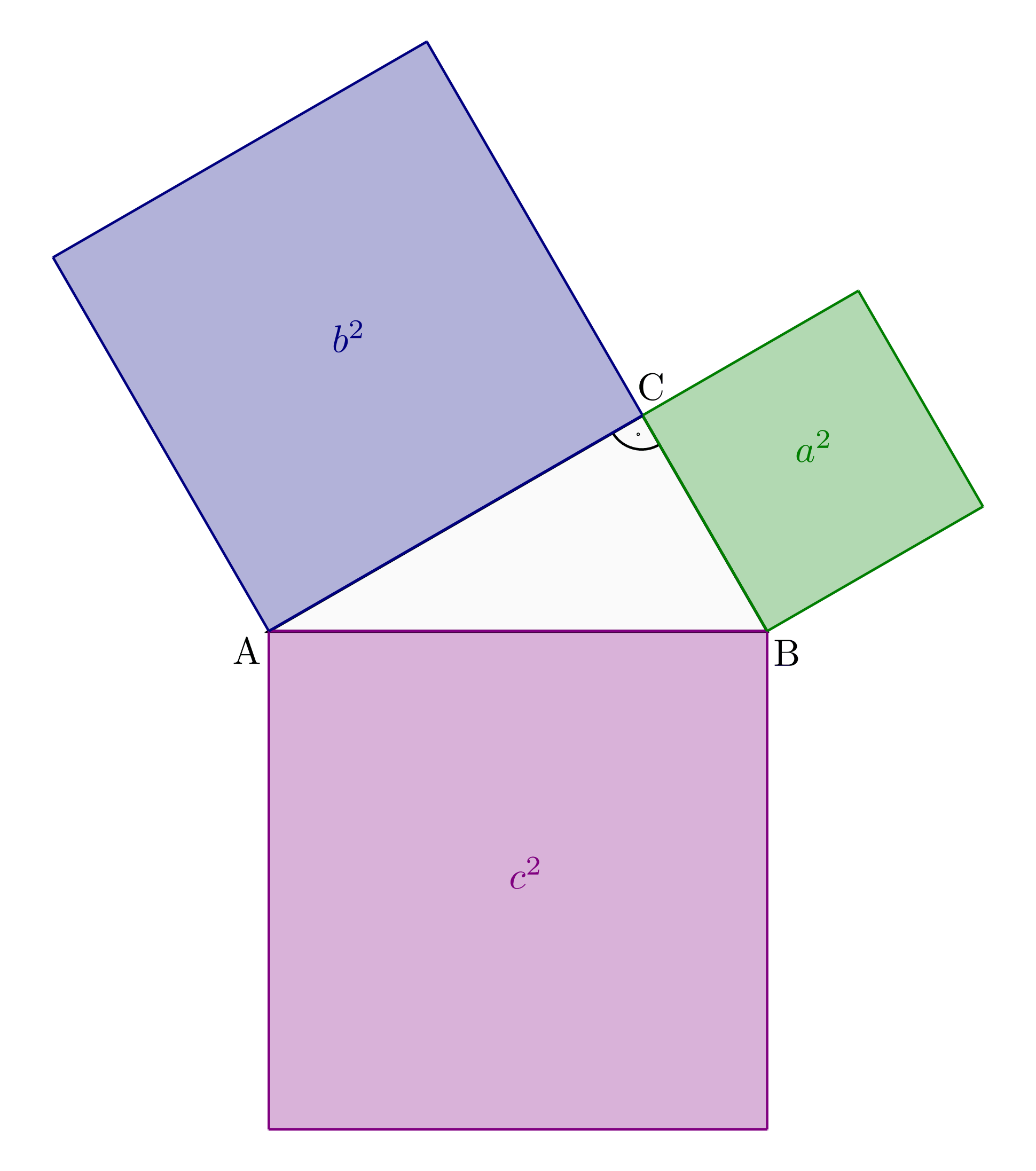
Der Satz von Pythagoras
Rechtwinklige Dreiecke weisen eine Besonderheit auf: Quadriert man die Längen
der Dreieckseiten, so entspricht die Quadratzahl 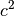 der längsten
Dreieckseite (der „Hypotenuse“) genau der Summe der Quadratzahlen
der längsten
Dreieckseite (der „Hypotenuse“) genau der Summe der Quadratzahlen 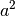 und
und 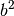 der kürzeren Dreieckseiten (der „Katheten“).
der kürzeren Dreieckseiten (der „Katheten“).
(3)¶
Diese als „Satz des Pythagoras“
bekannt gewordene Gesetzmäßigkeit lässt sich graphisch dadurch
veranschaulichen, indem man entlang der Hypotenuse  und den beiden
Katheten
und den beiden
Katheten  und
und 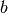 Quadrate mit den entsprechenden Seitenlängen
zeichnet und die Flächeninhalte miteinander vergleicht: Die Flächen der beiden
kleineren Quadrate
Quadrate mit den entsprechenden Seitenlängen
zeichnet und die Flächeninhalte miteinander vergleicht: Die Flächen der beiden
kleineren Quadrate 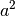 und
und 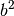 sind mit dem großen Quadrat
sind mit dem großen Quadrat
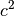 flächengleich.
flächengleich.
Der Satz des Pythagoras erweist sich in der Praxis als nützlich, um
zwei Bretter, Stangen o.ä. mit bekannten Längen  und
und 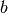 rechtwinklig zueinander anzuordnen. Löst man Gleichung (3)
nach der Länge der Verbindungslinie
rechtwinklig zueinander anzuordnen. Löst man Gleichung (3)
nach der Länge der Verbindungslinie  auf, so ergibt sich
auf, so ergibt sich
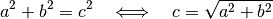
Liegen die Eckpunkte 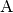 und
und 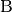 exakt um
exakt um
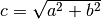 voneinander entfernt, so beträgt der Winkel zwischen
voneinander entfernt, so beträgt der Winkel zwischen
 und
und 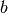 genau
genau ![\unit[90]{\degree}](../../_images/math/ed42da9b82869c64cf4a98987530ceace4d59e0e.png) . Geeignet ist
insbesondere das Längenverhältnis
. Geeignet ist
insbesondere das Längenverhältnis  , da hierbei
, da hierbei 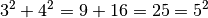 gilt; die Länge der Basis-Einheit kann frei gewählt werden.
gilt; die Länge der Basis-Einheit kann frei gewählt werden.
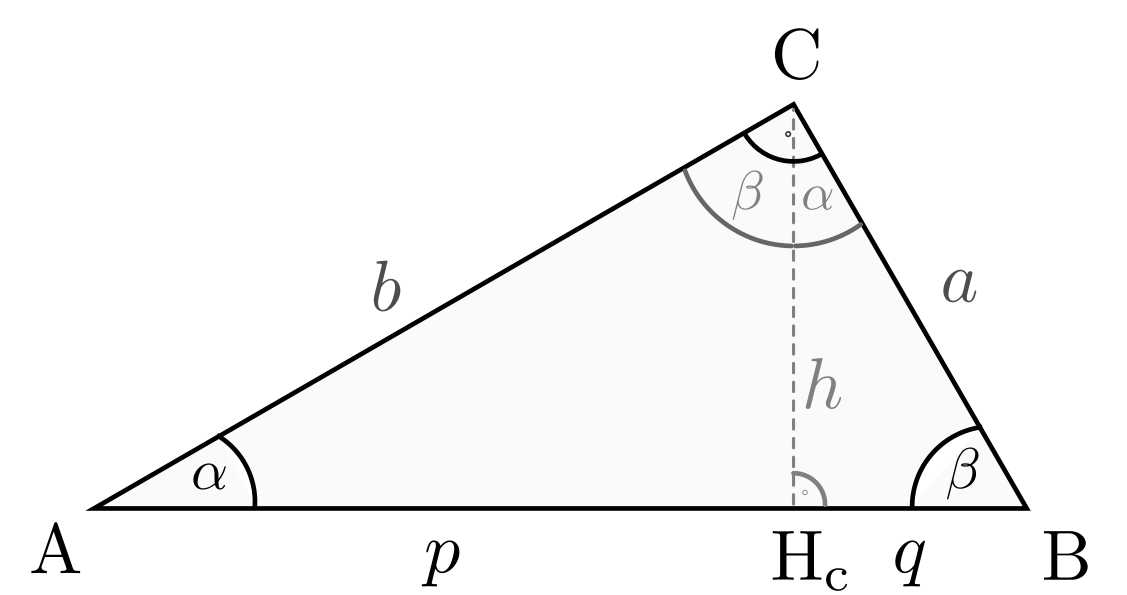
Höhen- und Kathetensatz
Im rechtwinkligen Dreieck gelten darüber hinaus zwei weitere Beziehungen:
- Höhensatz:
Das Produkt der beiden Hypotenusenteile
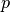 und
und 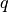 , die
rechts und links der Höhe
, die
rechts und links der Höhe  liegen, ist gleich dem Quadrat der
Höhe:
liegen, ist gleich dem Quadrat der
Höhe:
Kathetensatz: Das Produkt einer Kathete ist gleich dem Produkt aus der Hypotenuse
 und dem anliegenden Hypotenusenanteil:[3]
und dem anliegenden Hypotenusenanteil:[3]![a^2 &= c \cdot q \\[10pt]
b^2 &= c \cdot p](../../_images/math/63104ecb3362cdcf877c5cb3aaee6de756851daf.png)
Diese beiden Gesetzmäßigkeiten wurden bereits von Euklid entdeckt. Sie beruhen darauf, dass die
Dreiecke 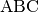 und die beiden durch die Höhe
und die beiden durch die Höhe  entstehenden
Dreiecke
entstehenden
Dreiecke 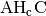 und
und 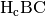 zueinander ähnlich sind: Alle
enthalten einen rechten Winkel und haben je eine Dreiecksseite gemeinsam, zudem
haben alle Dreiecke wegen Gleichung (1) den Winkel
zueinander ähnlich sind: Alle
enthalten einen rechten Winkel und haben je eine Dreiecksseite gemeinsam, zudem
haben alle Dreiecke wegen Gleichung (1) den Winkel
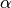 gemeinsam.
gemeinsam.
Aufgrund der Ähnlichkeit sind die Verhältnisse der Seitenlängen gleich, es gilt
beispielsweise für die Dreiecke 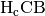 und
und 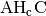 das
Längenverhältnis
das
Längenverhältnis 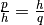 , das sich auch als
, das sich auch als 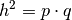 schreiben lässt und somit dem Höhensatz entspricht. Ebenso folgen
die beiden Kathetensätze aus den Längenverhältnissen
schreiben lässt und somit dem Höhensatz entspricht. Ebenso folgen
die beiden Kathetensätze aus den Längenverhältnissen  der Dreiecke
der Dreiecke  und
und 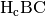 sowie
sowie
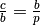 der Dreiecke
der Dreiecke 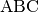 und
und
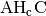 .
.
Weitere Eigenschaften
Auf weitere Zusammenhänge in Dreiecken wird im Abschnitt Trigonometrie näher eingegangen.
Anmerkungen:
| [1] | Gilt 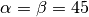 , so spricht man von einem
gleichschenklig-rechtwinkligen Dreieck. , so spricht man von einem
gleichschenklig-rechtwinkligen Dreieck. |
| [2] | Da die Seiten  und und 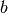 senkrecht aufeinander stehen,
stellen sie gegenseitig Basislinie und Höhe dar. senkrecht aufeinander stehen,
stellen sie gegenseitig Basislinie und Höhe dar. |
| [3] | Der Kathetensatz von Euklid beinhaltet auch den Satz von Pythagoras.
Addiert man nämlich die beiden Gleichungen
|


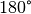 .
.

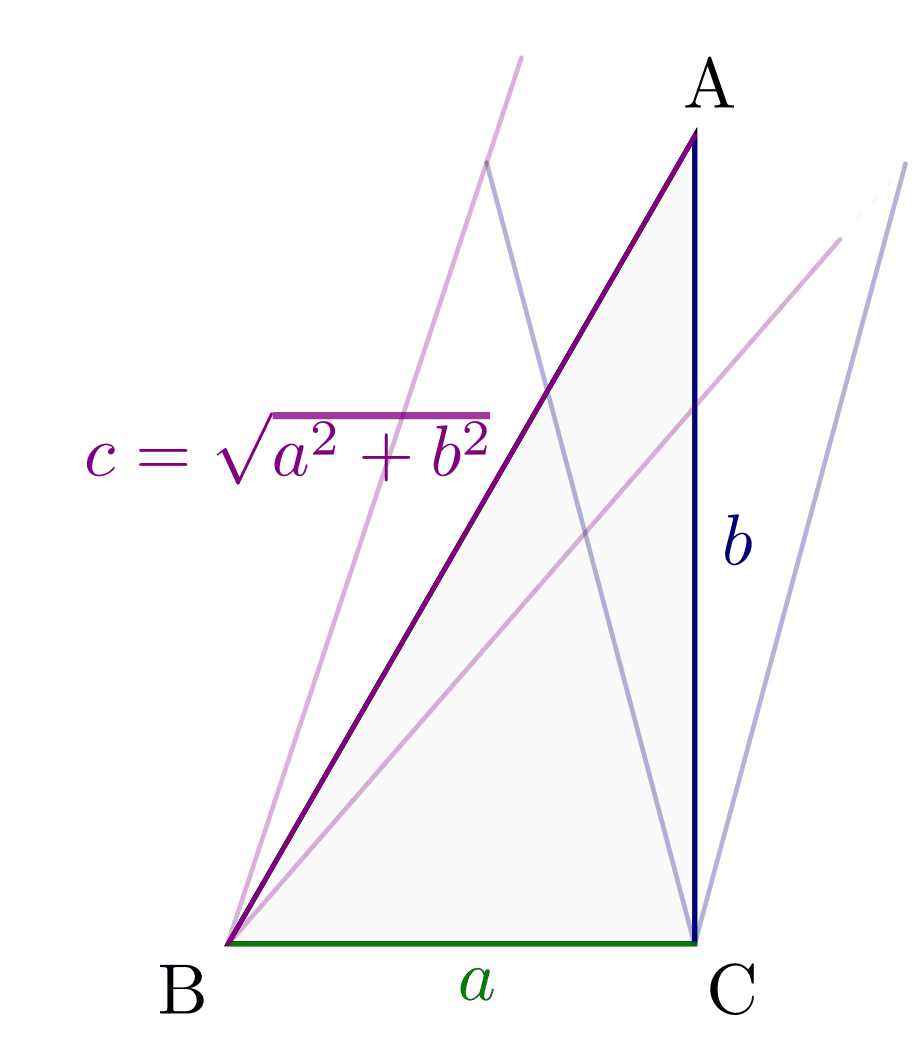
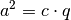 und
und
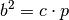 , so erhält man:
, so erhält man: