Aufgaben zur Optik¶
Ausbreitung des Lichts¶
Die folgenden Aufgaben beziehen sich auf den Abschnitt Ausbreitung des Lichts.
(*) Weshalb trifft nur ein kleiner Anteil des Sonnenlichts auf die Erde? Wieso erscheint uns das Weltall als dunkel?
(*) Weshalb kann Licht nicht – ähnlich wie Wasser – in einem Behälter eingefangen und aufbewahrt werden?
Reflexion von Licht¶
Die folgenden Aufgaben beziehen sich auf den Abschnitt Reflexion von Licht.
(*) Welche der Stoffe aus der folgenden Tabelle eignen sich dazu, Licht direkt (wie ein Spiegel) zu reflektieren? Welche Eigenschaft müssen ihre Oberflächen dafür besitzen?
Fensterglas Kalkstein Mehl Eis Mattglas Granit Kochsalz Schnee Kunststoff Diamant Zucker Wasser Holz Metall Sirup Nebel
(*) Weshalb können wir nachts Sterne sehen, die unvorstellbar weit entfernt sind, aber auf der Erde eine Lichtquelle kaum
![\unit[50]{km}](../_images/math/3e401ca38a5a5c2e22dbb64f475a8a284b832616.png) weit sehen?
weit sehen?
Lichtbrechung¶
Die folgenden Aufgaben beziehen sich auf den Abschnitt Lichtbrechung.
(*) Ein optisches Medium hat eine Brechzahl von
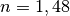 . Wie groß ist die
Lichtgeschwindigkeit
. Wie groß ist die
Lichtgeschwindigkeit  in diesem optischen Medium?
in diesem optischen Medium?
(*) Licht breitet sich sich in einem optischen Medium mit
![c=\unit[2,29
\cdot 10^8]{m/s}](../_images/math/940a58d1828fda25946a0d0381551e38183bfdef.png) aus. Wie groß ist die Brechzahl
aus. Wie groß ist die Brechzahl  des optischen
Mediums?
des optischen
Mediums?
(**) Ein Lichtstrahl, der sich zunächst in Luft
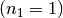 ausbreitet, fällt
in einem Winkel
ausbreitet, fällt
in einem Winkel 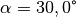 auf die Oberfläche eines transparenten
Materials mit einer Brechzahl
auf die Oberfläche eines transparenten
Materials mit einer Brechzahl 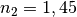 Lichtstrahl. Wie groß ist der
Winkel
Lichtstrahl. Wie groß ist der
Winkel 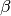 des gebrochenen Lichtstrahls?
des gebrochenen Lichtstrahls?
(**) Ein Lichtstrahl geht von Quarzglas
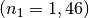 in Flintglas
in Flintglas
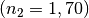 über. Wie groß ist hierbei die relative Brechzahl
über. Wie groß ist hierbei die relative Brechzahl
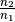 ? Wie groß ist der Winkel
? Wie groß ist der Winkel 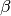 des
gebrochenen Lichtstrahls, wenn der Winkel des einfallenden Lichtstrahls
des
gebrochenen Lichtstrahls, wenn der Winkel des einfallenden Lichtstrahls
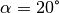 beträgt?
beträgt?
(**) Ein Lichtstrahl, der sich zunächst in Luft
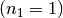 ausbreitet, fällt
in einem Winkel
ausbreitet, fällt
in einem Winkel 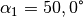 auf die Oberfläche eines
transparenten Materials. Der Winkel des gebrochenen Lichtstrahls beträgt
auf die Oberfläche eines
transparenten Materials. Der Winkel des gebrochenen Lichtstrahls beträgt
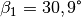 . Im gleichen Winkel
. Im gleichen Winkel 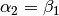 trifft der Lichtstrahl auf ein zweites transparentes Material, wobei der
Winkel des zum zweiten mal gebrochenen Lichtstrahls
trifft der Lichtstrahl auf ein zweites transparentes Material, wobei der
Winkel des zum zweiten mal gebrochenen Lichtstrahls 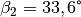 beträgt. Wie groß sind die beiden Brechzahlen
beträgt. Wie groß sind die beiden Brechzahlen 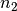 und
und 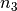 beider Materialien?
beider Materialien?
(**) Wie groß ist der Grenzwinkel
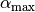 , wenn ein Lichtstrahl
von Diamant
, wenn ein Lichtstrahl
von Diamant 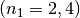 in Luft
in Luft 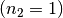 übergeht? Was
passiert, wenn für den Einfallswinkel
übergeht? Was
passiert, wenn für den Einfallswinkel 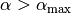 gilt?
gilt?
(*) In welchen zwei möglichen Fällen wird Licht, das von einem durchsichtigen Medium in ein anderes übergeht, nicht gebrochen?
Linsensysteme¶
Die folgenden Aufgaben beziehen sich auf den Abschnitt Linsensysteme.
(*) Eine Sammellinse hat eine Brennweite von
![f=\unit[150]{mm}](../_images/math/d91ddf02179924c3aa0d0c11912a254fb5beff61.png) . Wie
groß ist ihre Brechkraft
. Wie
groß ist ihre Brechkraft 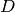 ?
?
(*) Eine Zerstreuungslinse hat eine Brechkraft von
![D=\unit[-4,0]{dpt}](../_images/math/8c0c47b3dc28e1dffd32c618e39ce3135741a709.png) . Wie groß ist ihre Brennweite
. Wie groß ist ihre Brennweite 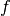 ?
?
(*) Welche Brennweite
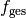 hat eine Kombination zweier
Sammellinsen, deren Brennweiten
hat eine Kombination zweier
Sammellinsen, deren Brennweiten ![f_1 = \unit[50]{mm}](../_images/math/c4ce2d84db19795d4382c791959611454315bb7b.png) und
und ![f_2 =
\unit[75]{mm}](../_images/math/6e035cdc797ce21d9f17db6f48c96030bbdc69f3.png) betragen?
betragen?
(**) Die Brechkraft einer dünnen Linse beträgt
![D = \unit[5,0]{dpt}](../_images/math/7146684713bfc6199a995fc1de325a69142faa98.png) . Ein
Gegenstand befindet sich im Abstand
. Ein
Gegenstand befindet sich im Abstand ![g = \unit[60]{cm}](../_images/math/5249f9030a87827dfa30acac1f1d2027e5920dd1.png) vor der Linse.
In welcher Entfernung
vor der Linse.
In welcher Entfernung 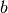 von der Linse befindet sich das Bild des
Gegenstands? Wie groß ist der Abbildungsmaßstab
von der Linse befindet sich das Bild des
Gegenstands? Wie groß ist der Abbildungsmaßstab 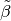 ?
?
(**) Eine Zerstreuungslinse hat eine Brechkraft von
![\unit[-8,0]{dpt}](../_images/math/e3133ef2b6a9b5d095b4c57650632207a5c84b8b.png) .
Wie groß ist die Brennweite des der Linse, und an welcher Stelle
.
Wie groß ist die Brennweite des der Linse, und an welcher Stelle 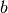 befindet sich das eines Gegenstands, der sich in
befindet sich das eines Gegenstands, der sich in ![g=\unit[9,0]{cm}](../_images/math/646df907e22a295b36db3d0111951b6c538b88f7.png) Entfernung von der Linse befindet?
Entfernung von der Linse befindet?
Optische Geräte¶
Die folgenden Aufgaben beziehen sich auf den Abschnitt Optische Geräte.
(*) Ein Kepler-Fernrohr hat ein Objektiv mit einer Brennweite von
![f_{\mathrm{Obj}} = \unit[32]{cm}](../_images/math/0aeb37b429965a0dfc0018befacf8c7af4ba810d.png) und ein Okular mit einer Brennweite
von
und ein Okular mit einer Brennweite
von ![f_{\mathrm{Ok}} = \unit[4]{cm}](../_images/math/fd5f623df1cfc0fae7be8b0f5f724d87480c2edf.png) . Welche Vergrößerung hat das
Fernrohr insgesamt?
. Welche Vergrößerung hat das
Fernrohr insgesamt?
