Lösungen zur elementaren Geometrie¶
Stereometrie¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Stereometrie.
Das Volumen einer Kugel mit Radius
![r = \frac{d}{2} = \unit[0,5]{\mu m}](../_images/math/7b60619a8baf1e33657daa3de7e08bb9236e304f.png)
beträgt:![V_{\mathrm{Tropfen}} = \frac{4}{3} \cdot \pi \cdot r^3 = \frac{4}{3}\cdot
\pi \cdot \left( \unit[0,5 \cdot 10^{-6}]{m} \right)^3 \approx \unit[5,236
\cdot 10^{-19}]{m^3}](../_images/math/81556c93396b4288ff89e31a203d321a840012f2.png)
Das insgesamt versprühte Volumen beträgt
![V_{\mathrm{ges}} = \unit[5]{ml}
= \unit[5 \cdot 10^{-3}]{dm^3} = \unit[5 \cdot 10^{-6}]{m^3}](../_images/math/4cae3dadd39e3a47888f9280c818ad966702fe2b.png)
, weil
![\unit[1]{dm} = \unit[\frac{1}{10}]{m}](../_images/math/9f780be06a160d7aa7608650e1da20dc5e55861b.png)
ist und somit
![\unit[1]{dm^3} = \left( \unit[\frac{1}{10}]{m} \right)^3 =
\unit[10^{-3}]{m}^3](../_images/math/f551f338ac7293ef3275e5309406251463417218.png)
. Für die Anzahl 
der entstehenden Tröpfchen ergibt sich
somit:![n = \frac{V_{\mathrm{ges}}}{V_{\mathrm{Tropfen}}} = \frac{\unit[5 \cdot
10^{-6}]{m}}{\unit[5,236 \cdot 10^{-19}]{m^3}} \approx 9,55 \cdot 10^{12}](../_images/math/bd5d8a039c5b8cf166edbe3a4797148a06c471c5.png)
Es entstehen somit knapp
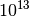Tröpfchen – also knapp 
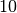Billionen!